钢管混凝土拱桥地震破坏模糊评估方法

谢开仲，莫永辉，蒙方成，周如意

（1.广西大学 土木建筑工程学院，南宁530004；2.广西贺州市城市建设投资开发集团有限公司，广西 贺州542800）

近年来，世界范围内地震频发，对桥梁工程是一个很大的考验，在不同强度的地震后桥梁特别是钢管混凝土拱桥的损伤和破坏程度的定量评估研究比较少，本文根据钢管混凝土拱桥各部分受力特点建立双重准则破坏模型，并研究基于模糊理论和层次分析法的地震损伤破坏模糊评估方法，建立钢管混凝土拱桥的有限元非线性分析模型，在地震反应分析的基础上，对钢管混凝土拱桥在震后的破坏进行评估，为桥梁的管养和加固维修提供科学可靠的依据。

1 各部分双重准则的破坏模型

根据钢管混凝土拱桥各部分受力特点［1］，建立变形或强度和能量的双重破坏准则［2］，主要是根据构件在受地震力作用下，产生变形或内力和累积耗能，当两个因素达到了构件的承受能力，构件就发生破坏。

根据双重破坏准则［3－6］，求出钢管混凝土拱桥各构件破坏指数。

1.1 拱肋弦杆

钢管混凝土拱肋弦杆主要承受轴力和弯矩作用［7］，引入压弯系数λ（即轴力和弯矩组合系数），拱肋弦杆的破坏指数为：

式中压弯系数λ为：

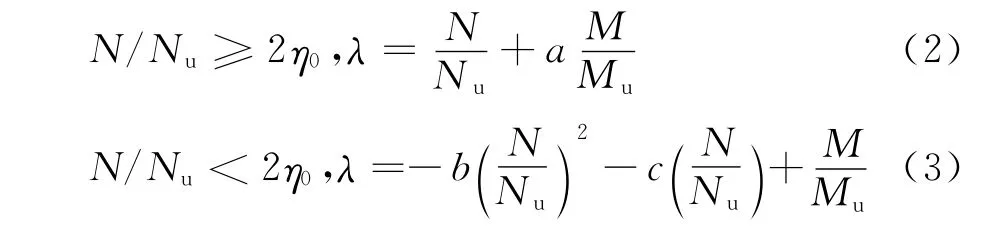
1.2 拱肋腹杆

腹杆主要是轴向力破坏，其破坏指数为：

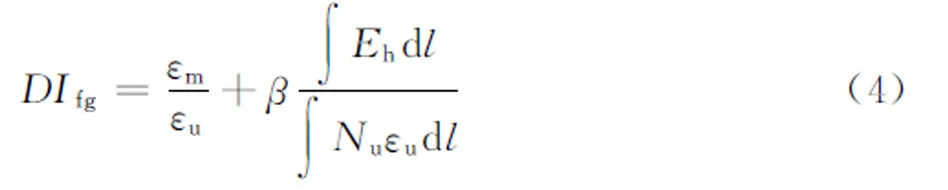
1.3 横向联系

横向联系主要受弯破坏，其破坏指数为：

1.4 吊杆

吊杆为受拉破坏［8］，其破坏指数为：

1.5 吊杆横梁

吊杆横梁为受弯破坏，破坏指数为：

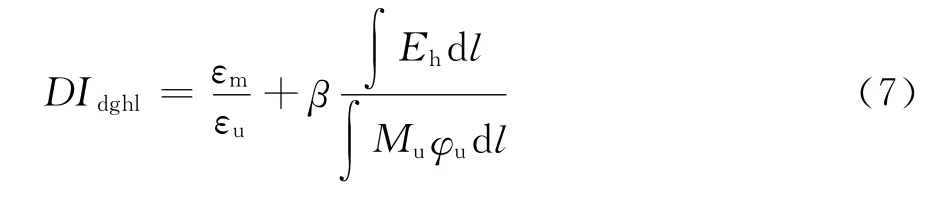
其中

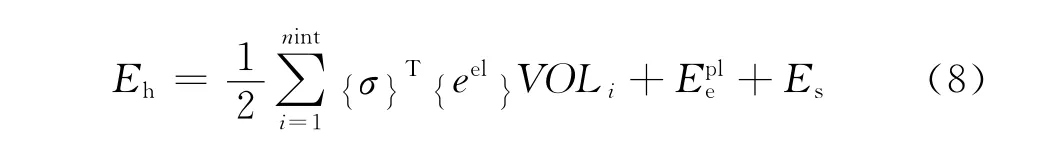
各式中DI为破坏指数，λm为拱肋弦杆构件截面最大的压弯系数，λu为弦杆的极限压弯系数，其值为 1，a＝1－2η0，b＝（1－ζ0）／η20，c＝2（ζ0－1）／η0，ζ0＝1＋0.18ξ1.13，套箍系数ξ＝（As／Ac）·（fy／fck），As为钢管面积，Ac为核心混凝土面积，fy为钢材的屈服强度，fck为混凝土抗压强度标准值，ξ≤0.4时，η0＝0.5－0.245·ξ，ξ＞0.4时，η0＝0.5－0.245·ξ，N为拱肋弦杆构件的轴力；M为拱肋弦杆构件的弯矩；Nu为构件达到屈服时的轴向压力；εm为构件截面所达到的最大轴向应变；εu为构件受压破坏时的轴向应变；Mu为杆端达到弯曲破坏时的弯矩；Eh为截面累积能量；nint为积分点个数；σ为应力矩阵；εel为弹性应变矩阵；VOL为积分点体积；Eepl为塑性应变能；Es为应力硬化能；β是系数，根据文献［3］回归统计得出β＝0.138 7；φm为构件截面所达到的最大弯曲曲率；φu为极限弯曲曲率。

2 权重体系的建立

各杆件及各部件的权重值的确定是根据每根构件在地震力作用过程中累积的地震能量来计算，表征其在构件和部件的破坏指数中的作用大小，所以采用权重系数w来表示。

弦杆杆件i的权重为

同理可以求出其他部件的权重值如腹杆杆件的（wi）fg、横向联系杆件的（wi）hx、吊杆杆件的（wi）dg和吊杆横梁杆件的（wi）dghl。

弦杆的破坏指数权重值为

同理可以求出腹杆、横向联系、吊杆和吊杆横梁的部件权重值。

3 基于模糊理论及层次分析法的地震破坏模型

3.1 因素集

对地震破坏评判因素按钢管混凝土拱桥各部件分类。三级为整桥地震破坏指数，二级评判因素主要部件有拱肋弦杆、腹杆、横向联系、吊杆和吊杆横梁；一级评判因素中的拱桥部件的杆件，构件破坏指数DI。评估时先对各部件的所有构件作为单个对象进行评估，再对部件作为对象进行评估，最后对整桥作为对象评估。

3.2 评价集

我国相关桥梁抗震规范没有对震害指数和相应的震害程度进行规定，根据文献［9－10］对钢管混凝土拱桥的地震破坏指数和震害程度规定。

将钢管混凝土拱桥的地震破坏指数程度分为：基本完好，轻微破坏，中等破坏，严重破坏和倒塌，对应的破坏指数值为：0～0.10，0.10～0.30，0.30～0.50，0.50～0.70，＞0.70。

3.3 隶属函数

隶属函数采用梯形分布，见图1。

图1 地震破坏指数隶属函数

3.4 模糊算法

模型IV：M（·，⊕）

模型IV采用乘法运算和有界和运算两种运算，综合评价模糊子集B～的元素bj用两式表示

3.5 钢管混凝土拱桥地震破坏的性能目标

钢管混凝土拱桥在不同强度地震作用下会产生相应的损伤和破坏，需要对其进行地震破坏评估，地震破坏评估涉及到建立合理的结构地震破坏模型和确定地震破坏的性能目标及相关指数的允许值［DI］。

根据文献［9］定义建筑结构不同破坏程度的破坏指数和桥梁养护规范定义桥梁的地震破坏指数范围［10］把桥梁结构的地震破坏性能目标分为五级：Ⅰ基本完好，主要构件处于弹性状态，次要结构不需修复或稍微修复，DI（0～0.10）；Ⅱ 轻微破坏，主要构件进入弹塑性状态，混凝土构件产生小裂缝，次要构件轻微损伤，DI（0.10～0.30）；Ⅲ 中等破坏，主要受力构件大部分进入塑性，钢筋混凝土构件严重裂缝，较难修复，DI（0.30～0.50）；Ⅳ 严重破坏，主要构件大部分屈服，钢筋混凝土结构混凝土压裂、部分梁柱发生断裂，DI（0.50～0.70）；Ⅴ 倒塌，主要构件断裂、桥梁局部或整体倒塌，产生生命危险，DI（＞0.70）。

3.6 评估模型

首先计算出钢管混凝土拱桥各部件构件的地震破坏指数：弦杆、腹杆、横向联系、吊杆和吊杆横梁 ，根据这些杆件地震破坏指数的隶属函数建立底层地震破坏评估向量 ，根据各杆件的累积能量计算评估指标权重体系。

按照模糊运算模型IV：M（·，⊕）得出钢管混凝土拱桥二级评估等级向量，即5个主要部件的地震破坏指数的评估等级向量Ri，组成等级评判矩阵，再根据权重体系中各部件的权重求得三级评估等级向量，即整桥地震破坏指数评估等级向量R。

4 工程应用

南宁永和大桥为下承式变高度桁式钢管混凝土无铰拱桥，净跨径336m，计算跨径346m，设计净矢高为76.873m。拱肋弦杆：Q345，Φ1220×20mm，核心混凝土C50；腹杆：Q345，610×10mm；横向联系钢管：Q345，Φ920×10mm；吊杆：吊杆采用61Ф7的钢绞线；吊杆横梁：吊杆横梁截面见图2，钢材为Q345。

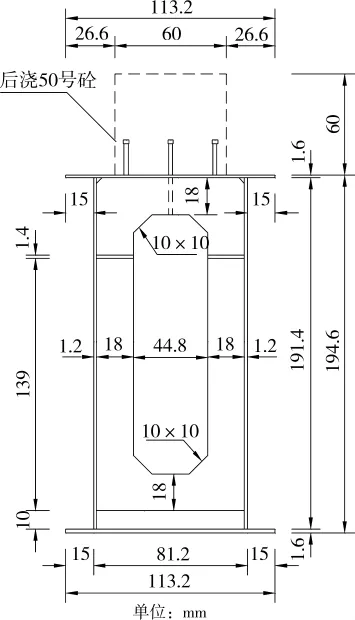
图2 吊杆横梁构造

4.1 计算模型

采用考虑剪切变形的空间梁单元模拟上下弦杆、竖斜腹杆、弦管缀管、钢横梁；用空间杆单元模拟吊杆；用空间板单元模拟弦管钢缀板、混凝土缀板、临时铰处加强钢板和桥面系；拱脚在桥墩处采用固定约束。桥纵向为X轴，横向（河流方向）为Y轴，竖向为Z轴，全桥有限元模型共3 672个节点，6 874个单元，有限元模型如图3所示。分析时的假定：1）在地震过程中地震动的3个主轴方向保持不变，且分别与桥梁的纵轴、横轴和竖轴重合；2）地震动的传播方向与桥梁的纵轴向重合。

图3 空间有限元模型

4.2 材料特性

C50：弹性模量Ec＝34 500MPa，密度为2 550kg／m3；轴心抗压标准值fck＝32.4MPa；Q345：弹性模量Ec＝206 000MPa，密度为7 850kg／m3；强度标准值，t≤16mm，fy＝345MPa；t＞16～35mm，fy＝325MPa；强度极限值，fu＝470MPa；吊杆：弹性模量Ep＝195 000MPa，密度为7 850kg／m3；强度标准值，fpk＝1 260MPa；强度极限值，fuk＝1 860MPa。

4.3 钢管混凝土拱桥各部分力学指标

钢管混凝土拱肋弦杆：Nu＝67 647kN，

Mu＝9 781kN·m。腹杆：强度极限轴力Nu＝10 596kN，对应应变εu＝3.26×10－3。横向联系：强度极限弯矩Mu＝28kN·m，对应曲率φu＝7.09×10－3。吊杆：强度极限轴力Nu＝4 731kN，对应应变εu＝9.54×10－3。吊杆横梁：强度极限弯矩Mu＝19 643kN·m，对应应变εu＝3.26×10－3，对应曲率φu＝3.35×10－3。

4.4 非线性地震反应分析

对计算模型进行非线性地震反应分析，模型中材料非线性的定义为钢材和钢丝绳采用二折线的弹塑性模型，混凝土的本构模型采用多线性随动强化模型，对应的应力应变曲线的计算选用《混凝土结构设计规范》（GB 50010—2010）公式。地震作用同时从X、Y和Z3个方向进行激励，地震波采用ELCentro波，不同烈度的地震按照相应的地震波强度进行折减，3个方向的地震波峰值比例取为1∶1∶0.6，地震波持时为10s，地震激励频率为0.02s，共分500步，采用Newmark－β方法求解结构系统动力方程。

4.5 地震损伤破坏模糊评估

分别对该桥在加速度峰值为0.1、0.2、0.4和0.8g的地震作用［10］和恒载作用下的损伤破坏进行评估。对在地震波作用下的钢管混凝土拱桥进行非线性分析，根据各部分每根构件的破坏模型求出相应的内力及累积能量，再求出构件的破坏指数，对各破坏指数进行模糊化，利用求出的权重体系求出各部件的破坏指数的模糊向量，完成一级模糊评估。加速度峰值为0.1、0.2、0.4和0.8g的地震作用下的二级模糊评估向量分别详见表1～4。三级模糊评估向量见表5。

表1 地震波加速度峰值为0.1 g的二级模糊评估向量

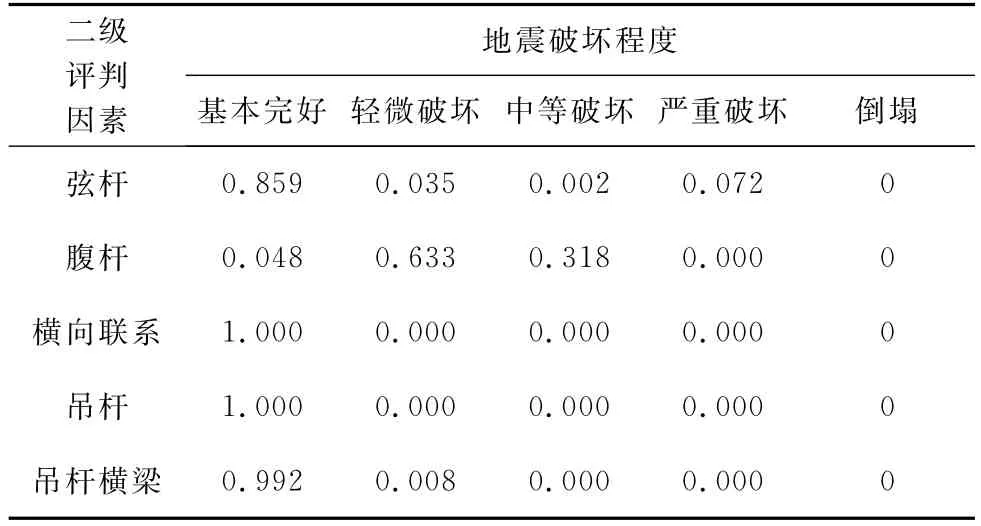
表2 地震波加速度峰值为0.2 g的二级模糊评估向量

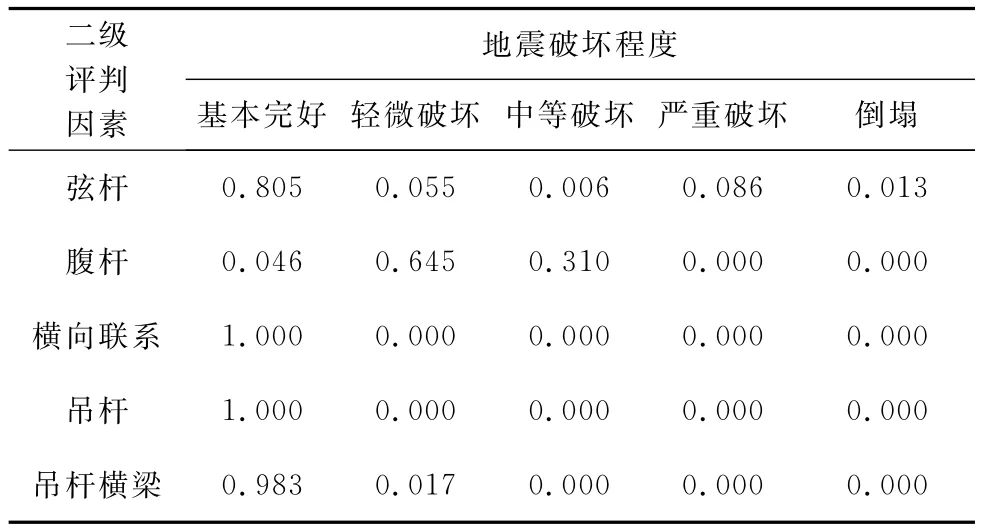
表3 地震波加速度峰值为0.4 g的二级模糊评估向量

表4 地震波加速度峰值为0.8 g的二级模糊评估向量

表5 3级模糊评估向量

由上述模糊评估结果可知，在加速度峰值为0.1、0.2、0.4和0.8g的地震作用下，整桥的破坏指数分别为0.150、0.152、0.172和0.318，说明在峰值为0.4g的地震作用下桥梁为轻微破坏，破坏随强度逐渐增大，在0.8g的地震作用下，为中等破坏。

在不同强度的地震作用下，拱肋弦杆和拱肋腹杆随着地震强度加大杆件由基本完好逐渐进入轻微破坏，直到峰值为0.8g时有部件进入屈服范围，整桥的破坏为中等破坏，局部弦杆构件和腹杆构件处在危险状态。因此利用基于层次分析法的模糊评估方法对钢管混凝土拱桥进行地震破坏评估比较直观了解桥梁各部件至各杆件的破坏程度，既能准确地求出整桥破坏指数，又能通过各级评估等级向量得到杆件、部件和整桥的地震破坏程度。

5 结 论

1）基于钢管混凝土拱桥的受力特点及破坏模式提出了基于变形或内力和累积耗能的双重破坏准则，为钢管混凝土拱桥实现破坏评估提供了途径。

2）利用模糊和层次分析法建立了钢管混凝土拱桥的地震破坏评估，得出杆件、部件和整桥的三级评估等级向量，可以得到杆件、部件和整桥在不同强度地震作用下的破坏程度，最后求出整桥地震破坏指标。

3）该桥的抗震设防烈度为7度，计算结果表明在9度地震作用下全桥处于轻微状态，满足抗震设计要求。

［1］钟善桐.钢管混凝土结构 ［M］.北京：清华大学出版社，2003

［2］牛荻涛，任利杰.改进的钢筋混凝土结构双参数地震破坏模型［J］.地震工程与工程振动，1996，16（4）：44－54.NIU Ditao，REN Lijie.A modified seismic damage model with double variables for reinforced concrete structures［J］.Earthquake Engineering and Engineering Vibration，1996，16（4）：44－54.

［3］史庆轩，钢筋混凝土基于性能的抗震研究及破坏评估［D］.西安：西安建筑科技大学，2002.

［4］Park Y J，Ang A H.Mechanistic seismic damage model for reinforced concrete ［J］.Journal of Structural Engineering，ASCE，1985，110（4）：35－38.

［5］Faleiro J，Oller S，Barbat A H.Plastic－damage seismic model for reinforced concrete frames［J］.Computers ＆Structures，2008，86（7－8）：581－597.

［6］Nasim K S，Michael D S，David I M.Evaluation of nonlinear static analysis methods and software tools for seismic analysis of highway bridges［J］.Engineering Structures，2008，30（5）：1335－1345.

［7］韩林海，杨有福.现代钢管混凝土结构技术［M］.北京：中国建筑工业出版社，2004.

［8］Gálvez J C，Benítez J M，Tork B，et al.Splitting failure of precast prestressed con－crete during the release of the prestressing force ［J］.Engineering Failure Analysis，2009，16（8）：2618－2634.

［9］Stephen W C，XU Y B，Paul W B.Seismic hazard and risk in Shanghai and estimation of expected building damage［J］.Soil Dynamics and Earthquake Engineering 2008，28（10）：778－794.

［10］JTG／T B02－01－2008 公路桥梁抗震设计细则［S］.2008.