考虑界面滑移的多自由度钢－混组合箱梁空间有限梁段法*

周凌宇，贺桂超

(中南大学土木工程学院，湖南 长沙 410075)

经典薄壁箱梁弯扭理论是建立在周边不变形和忽略剪应力对变形影响的基础上［1］，但是箱梁在偏心荷载作用下将产生纵向弯曲、扭转、畸变和横向挠曲［2］。组合箱梁中混凝土板与钢箱梁连接件刚度有限，在交界面处存在一定的水平滑移和掀起。对于完全剪力连接和部分剪力连接组合梁，必须考虑界面滑移对挠度的影响，同时组合箱梁桥跨度大、壁薄质小、恒载占荷载比例大、活载偏心所引起的扭转应力不能忽略，同时组合箱梁截面宽、肋距大，由“剪力滞效应”引起的剪切变形大，不能忽略［3－4］。

文献［5－6］提出了板桁框架法分析正交箱梁，文献［7］提出了桁梁梁段有限元分析空间桁架，文献［8－9］采用整体位移与局部位移叠加的方法，建立分析正交箱梁的梁段有限元法，文献［10－11］采用斜交坐标系，建立由板段组成的梁段的空间位移模型。以上分析均是建立在单一材料箱梁的基础上，而组合箱梁由于剪力连接度的影响，在界面处存在滑移，将明显影响组合箱梁的受力性能，而目前考虑界面滑移对组合箱梁受力性能影响的研究还不多见。

本文在以上箱梁空间分析的基础上，放弃周边不变形假定，考虑板件局部变形和组合箱梁界面滑移效应，建立组合箱梁梁段空间位移模型，并考虑几何非线性和材料非线性，利用势能驻值原理推导组合箱梁的“梁段有限元法”。在此基础上，编制相应的组合箱梁非线性空间有限元程序CBAP1.0，并与试验结果进行比较，计算结果表明组合箱梁梁段有限元法物理概念明确，计算精度高，收敛速度快，并可适用多种截面形式。

1 组合箱梁的界面滑移变分解法

图1所示的组合箱梁，钢箱梁与混凝土在界面上产生相对滑移，各自保持均匀的平截面伸缩。钢箱梁和混凝土板的纵向滑移应变可以表示为:

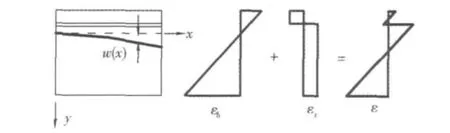
图1 组合箱梁滑移模型Fig.1 Slip model for composite box beam

根据梁的挠曲线近似微分方程，梁的弯曲应变可表示为:

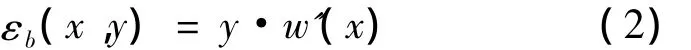
y为箱梁质点到中和轴的距离，将式(1)和(2)应变叠加，可以得到组合箱梁应变为:

应用变分原理，得到箱梁滑移效应的位移函数控制微分方程［4］:

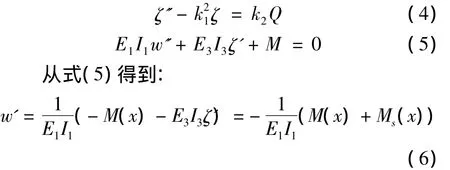
式中:Ms(x)=E3I3ζ＇。Ms(x)称为滑移效应的附加弯矩，它与滑移位移ζ(x)的一阶导数有关，且与E3I3成正比。从式(6)可知:考虑滑移效应，梁的曲率与弯矩已不再是经典梁理论中的关系，而是增加了附加弯矩Ms(x)修正项，滑移将增大结构曲率，降低构件刚度。

2 考虑滑移影响的梁段单元分析

2.1 基本假定

组合箱梁位移模型是构件组合箱梁梁段单元的关键，其关键步骤为:(1)将箱梁沿梁纵向离散为若干梁段单元，根据经典空间梁元理论和周边不变形假定计算箱梁内各质点在荷载作用下所产生的整体位移。(2)在各梁段单元内，沿梁轴线截取单位厚度箱梁空腹框架。并假设箱梁节点为刚节点。以刚节点之间杆件为基本单元，对箱梁空腹框架进行离散，根据箱梁横截面框架的变形特征，即将空腹框架离散成以下7种板件作为子单元:①顶板、底板单元;②斜腹板或;③竖直腹板;④悬臂板;⑤横隔板;⑥端横梁，计算各板件局部位移。(3)沿顶板、底板宽度设置与梁纵向位移协调的二次函数表示的纵向位移函数来考虑滑移位移。(4)叠加组合箱梁各质点位移整体位移、局部位移和滑移位移，形成组合梁段总体自由度，由此构成“组合箱梁板段单元”，计算箱梁梁段任意点的总位移。

分析时采用如下基本假定:(1)多室薄壁箱形梁顶板、底板与腹板的连接点为刚性节点。(2)钢箱梁翼板与混凝土之间栓钉层简化为一符合Goodman假设的夹层。该夹层不占据空间，剪力连接件用连续的等效的弹性介质代替;钢梁与混凝土产生相对滑移，各自保持均匀的平截面伸缩。(3)忽略各板的扭矩作用，薄壁箱梁顶板、底板、腹板的面外位移符合Kirchhoff假定。(4)仅考虑箱梁顶板和底板的剪力滞后。(5)忽略腹板与顶板、底板相交节点在横向的局部位移。

本文计算中箱梁部分用梁段单元离散来考虑箱梁局部变形，为简化计算，假定形心与扭心重合，如图2所示，箱梁变形前后的坐标均取为正交笛卡尔坐标系，坐标原点位于截面形心。图3所示为部分箱梁位移模型和局部位移模型(不含剪力滞后最大剪切转角)。图中“*”表示组合箱梁的纵向截面滑移。

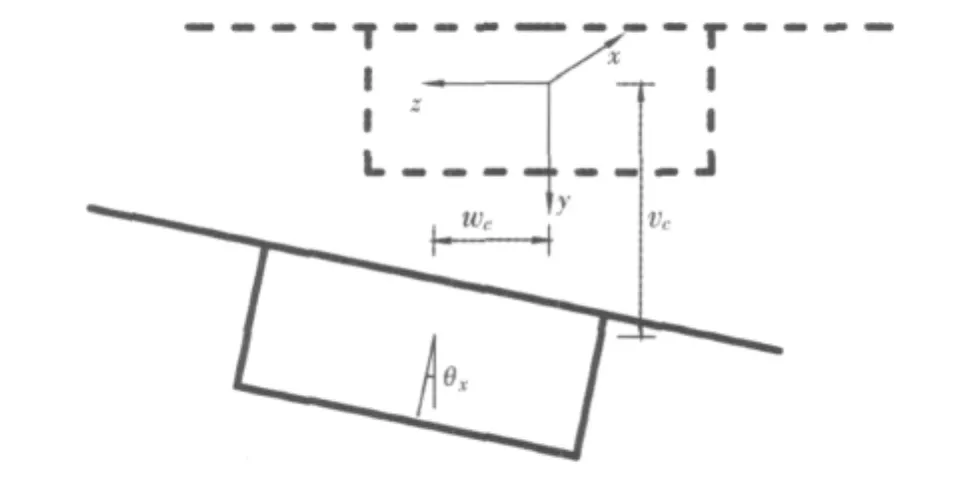
图2 梁段部分整体位移参数Fig.2 Overall displacement parameters of beam section

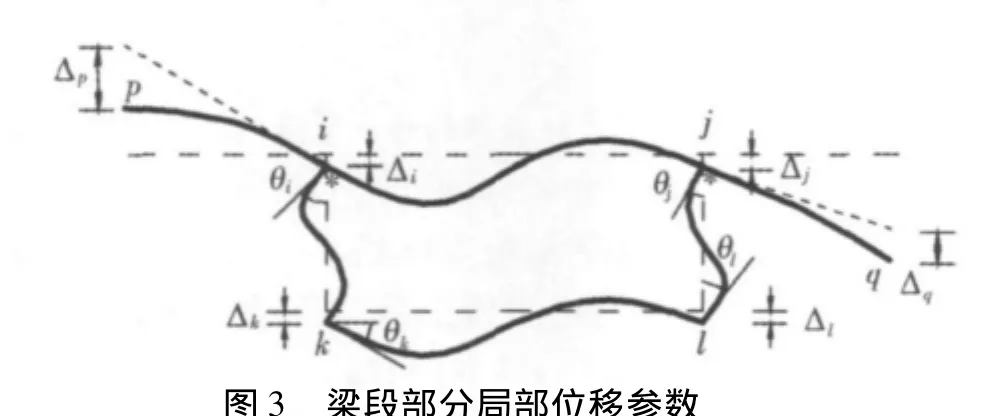
图3 梁段部分局部位移参数Fig.3 Local displacement parameters of beam section

2.2 组合箱梁整体位移计算

2.2.1 剪力滞后

梁弯矩经典理论的基本假定是变形的平截面假定，即弯曲正应力和位移沿梁宽方向均匀分布。这对于肋距不大的箱梁无疑是可以接受的。但是对于肋距大的组合梁，由于翼板中剪切变形沿宽度方向不均匀，引起远离腹板的顶板和底板纵向位移和应力较大的不均匀，即在近肋处翼板中产生应力和位移高峰，而远离腹板的产生纵向位移和应力的低谷。对于剪力滞后问题，本文在箱梁顶、底板的整体位移上叠加1个按二次多项式插值函数表示的纵向位移。采用如下方式描述［12］:

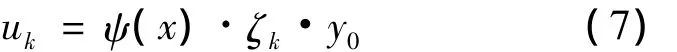
式中:uk为剪力滞后引起箱梁在顶、底板的非均匀纵向位移;ψ(x)为顶、底板剪切转角的最大差值;y0为顶、底板的中面距箱梁形心轴竖向距离;ζk为剪力滞位移函数。

2.2.2 扭转分析

伏拉勃夫和乌曼斯基在其提出的基于周边不变形的闭口截面刚性扭转第二理论中认为，表示翘曲程度的函数β含在σ和τ中，通过建立相关公式，求解β而得解。该理论得到广泛应用。该理论中认为，由扭转引起的截面纵向位移为［13］:

2.2.3 剪切变形的考虑

组合箱梁往往设计成薄壁大跨重载结构，组合箱梁内横向剪力所产生的剪切变形将引起梁的附加挠度，剪切变形影响不可忽略。经典梁理论中梁转角是梁变位的导数，没有考虑剪力产生的变位。梁变位后截面转角为θ，变形前垂直中心线的截面，变形后不一定保持垂直，转角与梁挠曲线的斜率之间并不存在简单的联系。与弯矩相对应的广义应变时相邻两截面的相对转角κ，它不是挠曲线的曲率，不过习惯上仍称为曲率。与剪力Q相对应的广义位移是剪切角γ，其相应关系为［14］:

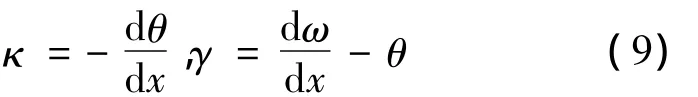
2.2.4 整体位移计算

根据经典梁理论模型，在纵向位移上叠加滑移位移和扭转位移，忽略截面转角对质点位移贡献的二阶微量，箱梁截面任一点整体位移为:

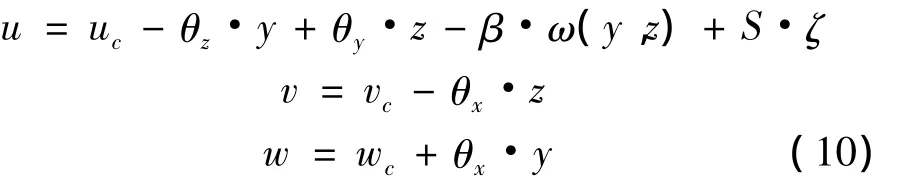
箱梁截面上任意点的位移可用该点所在截面的广义位移表示。如图4所示，其端点为单元的两节点，单元节点位移分量为:

式中:ui，vi，wi，θxi，θyi和θzi为节点 i沿 x，y和z方向的位移和转角，ζi和ζ＇i为节点i沿梁纵向的界面滑移和滑移应变，β为翘曲函数。图中用双箭头表示转角，用“*”表示界面滑移。

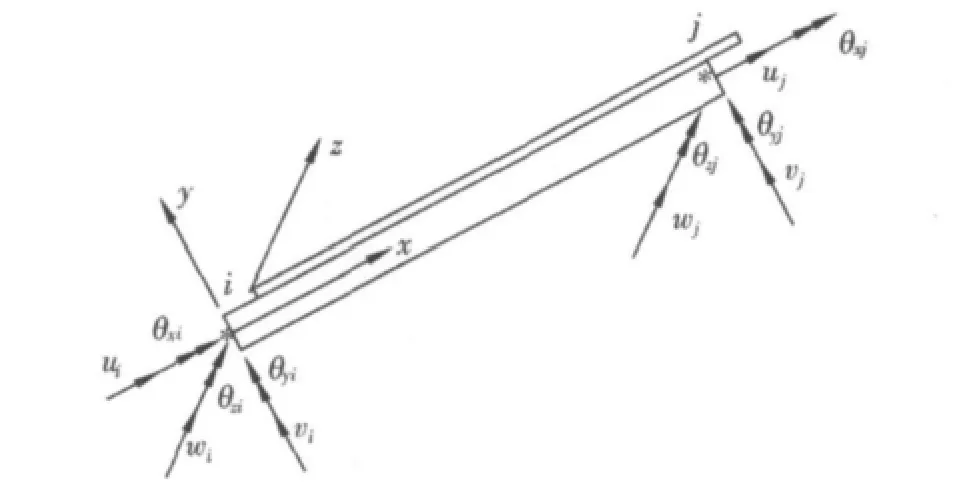
图4 空间梁单元节点位移Fig.4 Nodal displacements of space beam element

2.3 薄壁箱梁各板件局部位移计算

2.3.1 顶板和底板梁段单元局部位移

取组合箱梁横截面框架腹板之间的顶板(底板同)为基本单元，沿梁纵向取顶板微段，如图5所示。在顶板法线方向根据节点i和j处局部位移Δi，Δj，θi和 θj，顶板梁段面外局部位移取 Hermite插值函数得:

根据Kirchhoff假定，视翼板为Kirchhoff薄板，竖向局部位移引起翼板局部完全而在s轴方向产生位移，n为顶、底板竖向坐标，可得面内横向局部位移为:

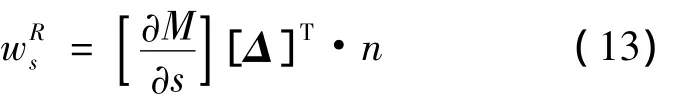
顶板面内纵向局部位移为:

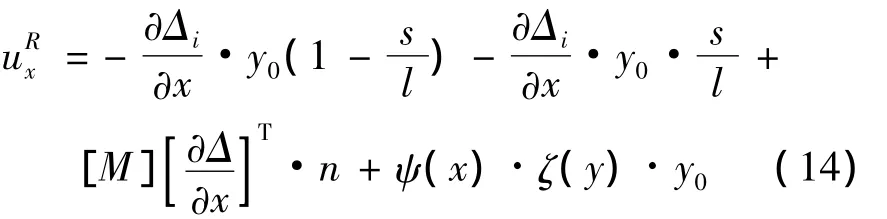
以上各式左端上标R表示局部位移，为了方便，i和j改为表示各板件梁段节点号，组合箱梁梁元节点号用m和n表示。

图5 顶板局部位移示意图Fig.5 Partial displacement of wing

2.3.2 斜腹板梁段单元局部位移为

斜腹板局部位移示意图如图6所示。考虑梁内纵向纤维之间存在挤压现象放弃在全截面内的平截面假定，而采用各板块在各自面内的纵向位移保持为平截面。根据前述分析模型，斜腹板的局部位移为:

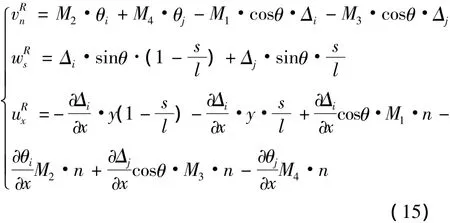
其中θ为斜腹板与箱梁截面坐标轴夹角。当θ=90°时，即可得到竖直腹板的局部位移。

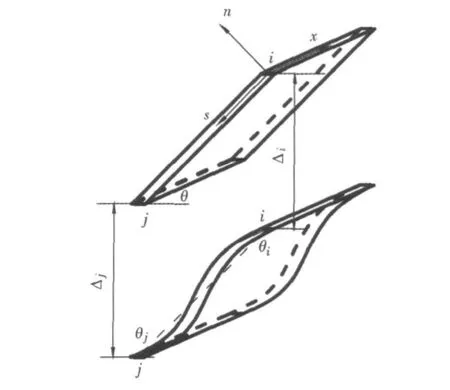
图6 斜腹板局部位移示意图Fig.6 Partial displacement of oblique webs

2.3.3 悬臂板梁段单元局部位移

图7所示为悬臂板梁段局部位移示意图。

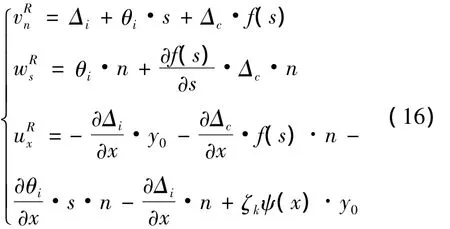
以上各式针对左悬臂板推导。对于右悬臂板，只需将式(16)中的s用l－s替换，即可得到右悬臂板的局部位移。

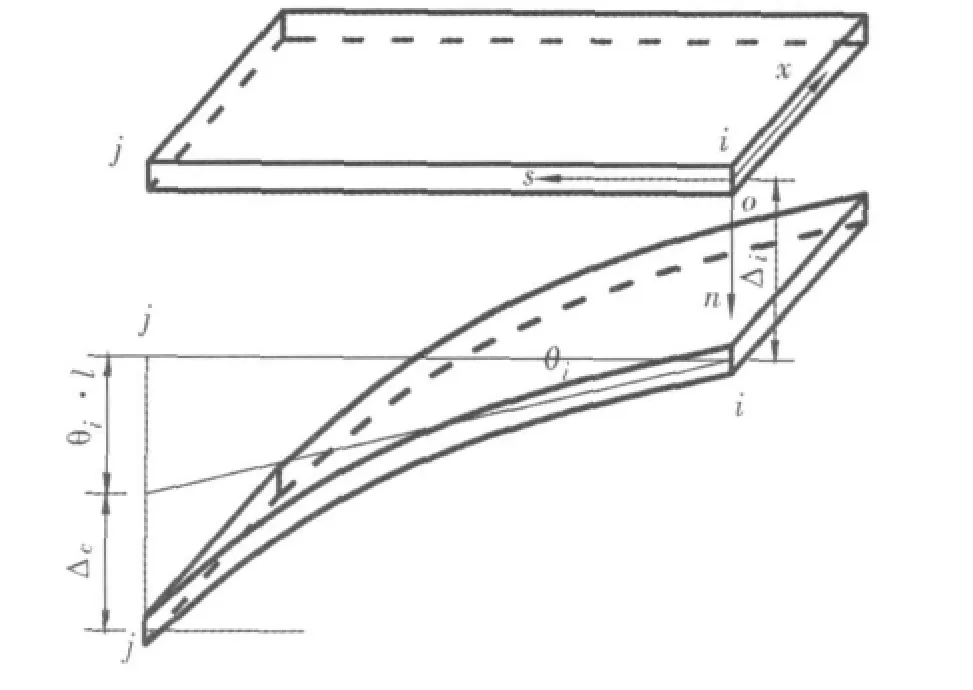
图7 悬臂板局部位移示意图Fig.7 Partial displacement of cantilever plate

2.3.4 横隔板梁段单元局部位移

采用考虑横隔板节点转角的位移模型［10］，同时忽略横隔板的平面外刚度。图8所示为考虑横隔板节点转角的局部位移示意图，忽略横隔板的面外弯曲。ij边到mn边采用线性插值描述质点面内位移沿y方向的变化。in边至jm边采用线性插值函数描述质点面内位移沿z方向的变化。同时保持边界上的位移与顶板、底板、腹板协调，得横隔板单元局部位移表达式为:

式中:P1，P2，P3，P4，Q2和 Q4表达式见文献［4］。

图8 横隔板局部位移示意图Fig.8 Partial displacement of diaphragm

2.4 梁段广义位移参数

箱梁是由顶、底板、腹板和悬臂板等单元组成，假设梁段节点号为m和n，图2示出了单室组合箱梁部分整体位移参数，各板件交点为 i，j，k，l，p 和q，如图3所示。根据前述基本思路和的基本假定，描述该梁段单元上所有节点位移需要广义整体位移、局部位移和滑移。根据以上梁段各板件广义位移参数的分析，可以得出梁段的广义位移参数。本文建立的“组合梁段单元”共有74个自由度，每个节点37个自由度，如下式所示:

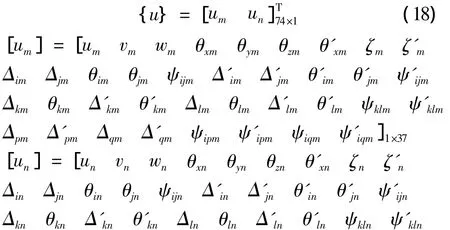
双下标的第一个下标表示交点号;第二个下标表示梁段单元节点号;三下标的前2个下标表示板段元件;第三个下标表示梁段单元节点号。

3 梁段单元刚度矩阵及求解

3.1 应变计算及虚功增量方程

将上述各板件的整体位移、滑移位移和局部位移叠加后即可得到箱梁梁段任一点的总体位移，根据文献［4］可得到各板件增量位移－应变关系，其应变非为线性部分和非线性部分。

根据U.L.列式虚功方程，可得顶、底板、腹板和悬臂板的虚功增量方程为:

3.2 单元荷载势能

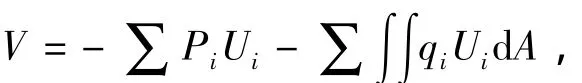
3.3 平衡方程

集合以上各板件的应变能可得结构总势能为:

式中:N为梁单元个数;Πe为梁单元应变能;为梁单元滑移应变能;V为外荷载势能。

以上为单元刚度矩阵和荷载列阵的推导，可编制有限元程序对多种截面形式的空间杆系结构进行分析计算。与通用有限元程序计算组合箱梁相比有如下优点:(1)前处理时，直接按简单梁单元方法进行离散，后处理时，可直接得到滑移、畸变、剪切变形等各位移量，前后处理简单;(2)本文方法适合不同边界条件的组合箱梁计算;(3)本文计算程序可以在一般杆系有限元计算程序的基础上简单改进而得。模型单元数量少，建模简单方便，前后处理工作简便，收敛迅速，计算时间短，并可方便计算多种截面形式。(4)改变顶、底板材料性质，该组合箱梁单元也可计算钢箱梁、混凝土箱梁。

4 算例验算

一简支钢－混凝土组合箱梁，跨度L=4.0 m，截面特性如图9所示［4］，混凝土弹性模量为3.25×104MPa，泊松比0.2;钢材弹性模量为2×105MPa，泊松比0.3，跨中作用集中荷载。根据本文提出的组合箱梁梁段有限元法理论编制的CBAP1.0有限元程序，将该梁单元划分为8个两节点空间梁段单元进行计算。

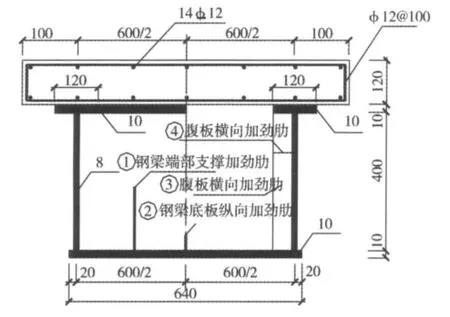
图9 截面尺寸(单位:mm)Fig.9 Dimensions of cross section(unit:mm)

图10和图11所示为考虑界面滑移效应和材料及几何非线性的荷载－挠度曲线和荷载－滑移曲线的本文算法计算值和实测结果。从图中可看出，本文计算结果与实测值较吻合，验证了本文算法和程序的正确性。

图10 荷载－挠度曲线Fig.10 Load － deflection curves

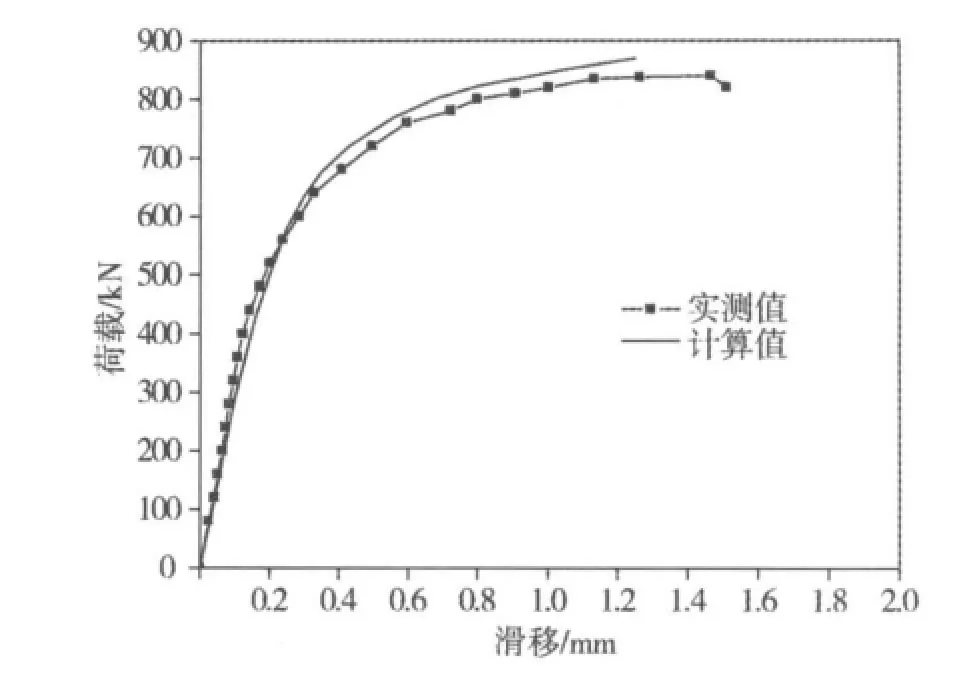
图11 荷载－滑移曲线Fig.11 Load － slip curves

5 结论

(1)根据组合箱梁滑移模型，建立了组合箱梁考虑滑移与剪切的空间梁元及其整体位移参数，根据周边不变形假设推导了组合箱梁整体位移与滑移位移。

(2)将组合箱梁整体位移、滑移位移与周边变形的局部位移叠加，推导了组合箱梁总体位移。

(3)根据各板件总体位移推导了各子单元的线性应变与非线性应变，根据最小势能原理推导了组合箱梁梁段单元刚度矩阵和荷载列阵。

(4)编制了组合箱梁非线性空间有限元程序，并与试验结果进行比较，结果表明组合箱梁梁段有限元法物理概念明确，计算精度高，收敛速度快。

［1］陈伯真，胡毓仁.薄壁结构力学［M］.上海:上海交通大学出版社，1998.CHEN Bo-zhen，HU Yu-ren.Thin－walled structure mechanics［M］.Shanghai:Shanghai Jiaotong University Press，1998.

［2］郭金琼.箱形梁设计理论［M］.北京:人民交通出版社，1991.GUO Jin-qiong.Box girder design theory［M］.Beijing:People’s Communications Press，1991.

［3］周凌宇，贺桂超.大跨度开口钢箱－混凝土组合箱梁有限元参数分析［J］.铁道科学与工程学报，2012，9(1):5－11.ZHOU Ling-yu，HE Gui-chao.Parametric analysis of long－span steel－concrete composite box beam［J］.Journal of Railway Science and Engineering，2012，9(1):5 －11.

［4］周凌宇.钢－混凝土组合箱梁受力性能及空间非线性分析［D］.长沙:中南大学土木工程学院，2004.ZHOU Ling-yu.Service behavior of steel－concrete composite box beams and triaxial nonlinear analysis［D］.School of Civil Engineering，Changsha:Central South U-niversity，2004.

［5］曾庆元.薄壁箱形梁计算的板梁框架法［J］.铁道学报，1981(3):92－104.ZENG Qing-yuan.A plate girder－frame method for the analysis of thin － walled box girders［J］.Journal of the China Railway Society，1981(3):92 －104.

［6］王荣辉，徐林荣，曾庆元.板桁组合结构空间计算的板桁梁段有限元法［J］.工程力学，1999，16(4):65－72，77.WANG Rong-hui，XU Lin-rong，ZENG Qing-yuan.Plate－truss deck section finite element method of spatial analysis for plate － truss composite structure［J］.Engineering Mechanics，1999，16(4):65 －72，77.

［7］曾庆元，杨 平.形成矩阵的“对号入座”法则桁架空间分析的桁段有限元法［J］.铁道学报，1986(8):48－59.ZENG Qing-yuan，YANG Ping.The“set－in－rightposition”rule for forming structural matrices and the finite truss－element method for space analysis of truss bridges［J］.Journal of the China Railway Society，1986(8):48－59.

［8］钟新谷，曾庆元，戴公连.单拱面预应力混凝土系杆拱桥极限承载力分析［J］.工程力学，1999，16(5):8－16.ZHONG Xing-gu，ZENG Qing-yuan，DAI Gong-lian.A-nalysis of the ultimate load of one－plate prestressed concrete box girder tide arch bridge［J］.Engineering Me-chanics，1999，16(5):8 －16.

［9］李 华，黄 羚，王道斌.考虑局部变形影响的薄壁箱梁几何非线性分析［J］.石家庄铁道学院学报，1999，12(3):10－13.LI Hua，HUANG Ling，WANG Dao-bin.Geometrical nonlinear analysis for thin－walled box girder in consideration of the effect of local deformation［J］.Journal of Shijiazhuang Railway Institute，1999，12(3):10 －13.

［10］盛兴旺.预应力混凝土斜交箱形梁分析理论与试验研究［D］.长沙:中南大学土木工程学院，2000.SHENG Xing-wang.Analytic theory and model test of prestressed concrete skew box girders［D］.Changsha:School of Civil Engineering，Central South University，2000.

［11］盛兴旺，曾庆元.斜交箱梁的板梁有限元法［J］.中国铁道科学，2004，25(3):55 －60.SHENG Xing-wang，ZENG Qing-yuan.A finite element method for slab beam segment of skew box girder［J］.China Railway Science，2004，25(3):55 －60.

［12］Mikkola M J，Paavola J.Finite element analysis of box girders［J］.J Struct Diviso，ASCE 1980 ST10:1343 －1357.

［13］伏拉勃夫.薄壁空间体系的建筑力学［M］.腾智明，译.北京:中国建筑工业出版社，1957.Volt LaBeouf.Building mechanical of thin － walled space system［M］.TENG Zhi-ming，translate.Beijing:China Architecture ＆ Building Press，1957.

［14］胡海昌.弹性力学变分原理［M］.北京:科学出版社，1981.HU Hai-chang.Variational principle of elasticity［M］.Beijing:Science Press，1981.