一种小半径曲线桥上无缝线路稳定性加强方案研究*

魏贤奎，王 平，庞 玲，陈 嵘

(1.西南交通大学高速铁路线路工程教育部重点实验室，四川 成都 610031;2.中铁二院工程集团有限责任公司，四川 成都 610031)

无缝线路消灭了大量的接头，提高了线路的平顺性［1］，在铁路建设中得到了广泛应用。近年来，随着高速铁路建设的飞速发展，桥梁在线路中所占比例逐步增大，更多的无缝线路铺设在桥梁上形成桥上无缝线路，然而，当桥梁位于小半径曲线上，桥上无缝线路的稳定性时常不能得到有效保障。桥上无缝线路通常要铺设护轨［2］，其目的是当列车脱轨时限制列车移动，以免列车撞击桥梁或自桥上坠下。本文利用护轨这一特殊结构，提出一种小半径曲线桥上无缝线路稳定性加强方案，即采用护轨横撑(材料为槽钢)将2根护轨连接起来形成桁架结构以提高轨道框架刚度，进而提高线路的稳定性。采用有限元法，建立考虑护轨作用的加强方案下无缝线路稳定性计算模型，研究这种加强方案对小半径曲线桥上无缝线路稳定性的提高效果。

1 加强方案介绍

加强方案主要用于半径小于600 m的曲线地段桥上无缝线路稳定性加强，方案设计如图1所示。加强地段桥上铺设新III型混凝土桥枕，按1667根/km铺设，护轨选用50 kg/m或60 kg/m钢轨，护轨接头夹板螺栓扭矩不小于400 N·m［3］，护轨横撑采用Q235的50 mm×37 mm×4.5 mm槽钢制作，主要考虑护轨为非受力结构，在护轨中心打孔不影响其用，而且护轨横撑施工简单、拆卸方便。

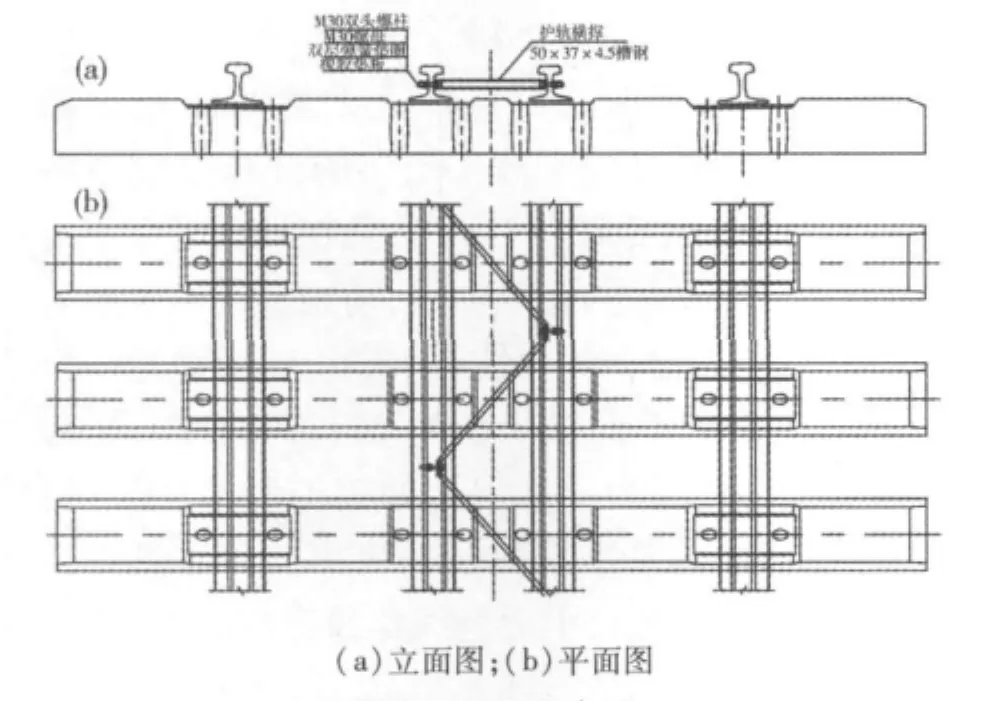
图1 加强方案图Fig.1 Graph of strengthening scheme

加强方案不仅考虑了护轨本身的抗弯刚度，通过护轨横撑将2根护轨连成一个整体后，又增加了护轨断面对线路中心的抗弯刚度，轨道框架抗弯刚度得到较大提高，对小半径曲线地段桥上无缝线路稳定性的提高会有比较好的效果。

2 加强方案下无缝线路稳定性计算模型

2.1 基本假设

在加强方案下，桥上无缝线路结构变得较为复杂，进行如下假设:

(1)假设线路初始弯曲形状是对称的，护轨和基本轨有着同样的初始弯曲;

(2)不虑道床纵向阻力和扣件阻矩的影响;

(3)不考虑护轨接头对轨条刚度的影响;

(4)假设基本轨和护轨扣件横向刚度为线性，轨枕横向阻力位非线性;

(5)不考虑护轨横撑温度力的影响(试算证明几乎没有影响);

(6)不考虑护轨横撑对护轨温度力的影响;

(7)不考虑其他加强方案对稳定性计算的影响;

(8)模型长度取为24 m，可消除边界条件影响，基本轨和护轨两端固定。

2.2 计算模型

有限元法计算无缝线路的稳定性的可行性已经得到了验证［4－7］，本文采用有限元法建立考虑护轨作用的加强方案无缝线路稳定性计算模型如图2所示，计算模型中按轨枕间距、扣件间距及横撑节点间距划分单元，把基本轨、护轨和轨枕离散成有限个单元的集合体。

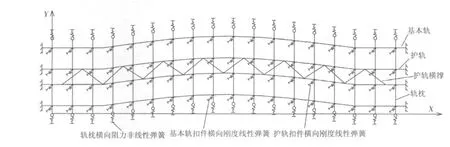
图2 加强方案无缝线路稳定性计算模型Fig.2 Calculation model of CWR stability under strengthening scheme

计算模型在有限元计算软件ANSYS中实现，基本轨、护轨、轨枕及横撑采用空间梁单元BEAM54模拟，轨枕横向阻力用非线性弹簧单元COMBIN39模拟，基本轨和护轨扣件横向刚度用线性弹簧单元COMBIN14模拟。

2.3 计算方法

图2所示的计算模型需考虑护轨中温度力的影响，采用荷载增量法［8］计算轨道框架最大横向位移达到2 mm时基本轨的升温幅度，考虑1.3倍的安全系数后得到基本轨的允许温升(以下简称Δtc)，由Δtc所确定的温度力即是基本轨中所能承受的最大纵向力，对于路基上的无缝线路，该纵向力为基本轨温度压力，而对于桥上无缝线路，则为基本轨温度压力、伸缩附加压力或挠曲附加压力之和［9］。

3 护轨对无缝线路稳定性的影响分析

3.1 护轨中最大温度力分析

由于计算模型中考虑了护轨的作用，因此就必须要考虑护轨中的温度力，然而，目前桥上无缝线路设计检算时没有考虑护轨作用［9－10］，对于护轨中的温度力分布规律等缺乏研究，在此本文对护轨中可能存在的最大温度力进行分析，基本假定和计算参数如下:

(1)不考虑由梁轨相互作用对护轨中产生附加力的影响。

(2)基本轨扣件阻力较大，可将轨枕牢牢扣压住，则护轨纵向滑动时阻力应按护轨扣件系统取值，根据文献［3］，护轨扣板螺栓为Φ24 mm螺旋道钉，螺栓扭矩一般为30～50 N·m，计算确定单根轨枕上一组护轨扣板扣压力为6～10 kN，综合摩擦系数取0.8，当轨枕间距为0.6 m时，按最不利考虑护轨扣件纵向阻力梯度为13.33 kN/m。

(3)护轨为定长25 m的50 kg/m或60 kg/m钢轨。

(4)护轨的接头阻力按正线钢轨接头阻力取值，根据文献［1］，当接头扭矩为400 N·m时，接头阻力取200 kN;

(5)极端条件下，护轨升温幅度取为50℃。

综合以上假定和计算参数，求得50 kg/m或60 kg/m钢轨护轨中的温度力分布图，如图3所示。

由图3可知:护轨中最大温度力为366.6 kN，则对于50 kg/m钢轨护轨折算成温度相当于22.9℃，对于60 kg/m钢轨护轨折算成温度相当于19.5℃。

图3 护轨温度力分布图Fig.3 Temperature force profile of guard rail

3.2 护轨对无缝线路稳定性影响

基本参数:基本轨采用60 kg/m钢轨，弹性模量为2.06 ×105MPa，热膨胀系数 α =1.18 ×10－5/℃，截面积为77.45 cm2，惯性矩为524 cm4;轨枕间距为0.6 m，轨枕横行阻力q(单位为N/cm)与横向位移y的方程式为q=25.11 －1012.87y+1014.1y3/4;轨道初始弹性弯曲矢度foe=3 mm，初始塑性弯曲矢度fop=3 mm，初始不平顺弦长取 l0=4 m［10］;基本轨和护轨扣件横向刚度取50 kN/mm。

首先按现有规范［9－10］计算无缝线路稳定性(即不考虑护轨的影响)，在图2的计算模型中将护轨扣件横向刚度取为0即可，且在计算模型中考虑初始弹性不平顺为正弦曲线，初始塑性不平顺为圆曲线，暂不考虑初始弹性不平顺引起的弹性内力的影响，分别计算曲线半径为 250，300，350，400，450，500，550和600 m 的 Δtc如表1所示，表中的计算结果可作为基准来衡量护轨本身和加强方案对小半径曲线地段桥上无缝线路稳定性的影响。

表1 现有规范ΔtcTable 1 The Δtcunder modern standardization

考虑3.1节中求得的护轨温度力，在图2所示的计算模型中将护轨横撑的相关参数取为0，对比表1，分别计算护轨采用50 kg/m或60 kg/m钢轨时的Δtc提高量如表2和图4所示。

由表2和图4可知:当考虑护轨作用时，曲线半径小于600 m的地段，无缝线路的稳定性都呈现不同程度的降低，按现有规范检算无缝线路稳定性是偏于不安全的;曲线半径越小，无缝线路稳定性降低量越大，主要是因为护轨抗弯刚度对稳定性的提高量要比护轨温度力对稳定性的削弱量要小;在同样曲线半径条件下，采用60 kg/m钢轨护轨比50 kg/m钢轨护轨的效果要好。这主要是因为2种护轨内的温度力相同，但60 kg/m钢轨护轨的抗弯刚度要大些;建议在进行小半径曲线桥上无缝线路稳定性检算时要考虑护轨的影响。

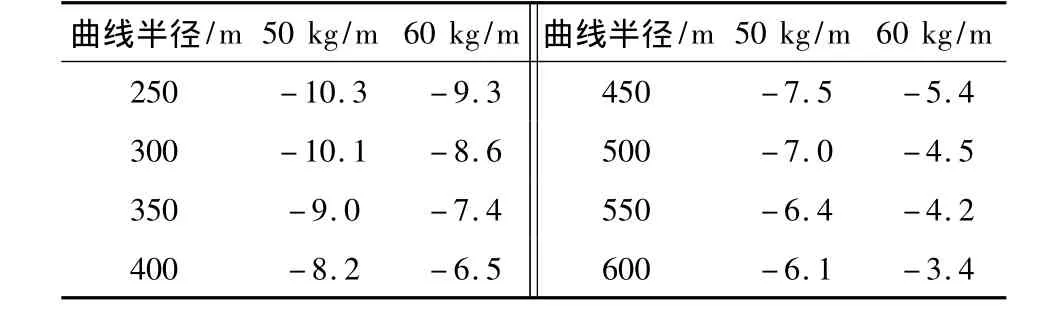
表2 考虑护轨Δtc提高量Table 2 Improvement of Δtcwith guard rail considered

图4 Δtc提高量与曲线半径关系Fig.4 Relationship between improvement of Δtcand curve radius

4 加强方案对无缝线路稳定性的影响分析

4.1 加强方案对无缝线路稳定性影响

取基本计算参数与3.2节中的相同，仍考虑3.1中求得的护轨温度力，对比表1分别计算加强方案下护轨采用50 kg/m或60 kg/m钢轨时的Δtc提高量如表3和图5所示。

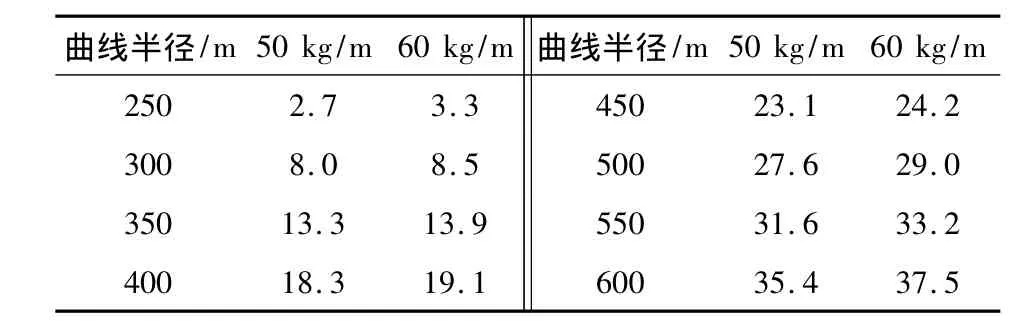
表3 加强方案Δtc提高量Table 3 Improvement of Δtcunder strengthening scheme

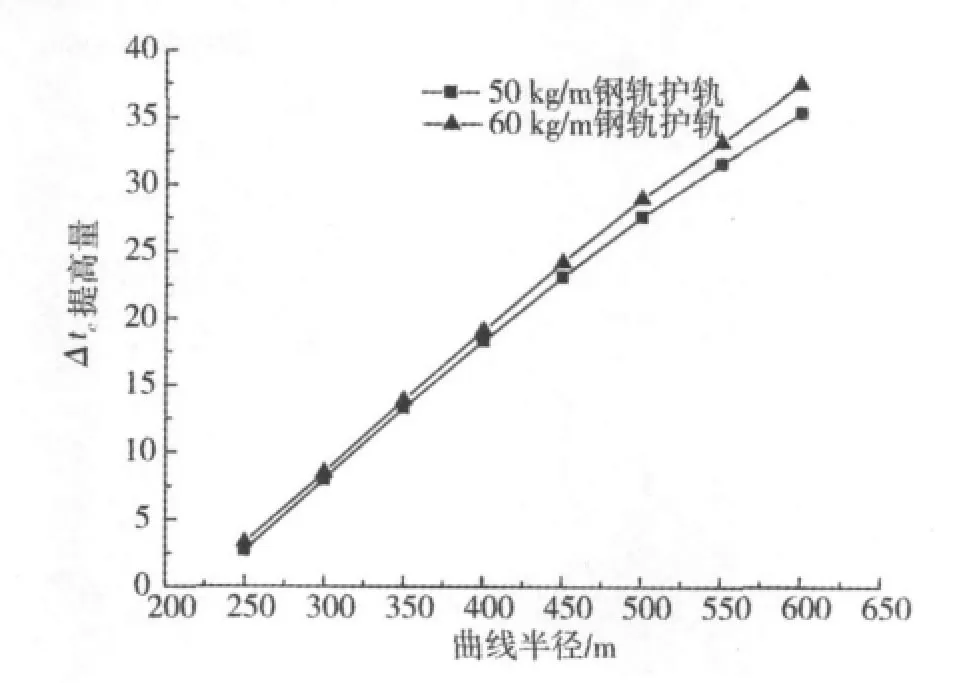
图5 加强方案Δtc提高量与曲线半径关系Fig.5 Relationship between improvement of Δtcunder strengthening scheme and curve radius

由表3和图5可知:加强方案提高了轨道结构的框架刚度，使Δtc得到提高，对无缝线路稳定性的提高有很好的效果;当曲线半径较小时，Δtc提高量要小些。这是因为曲线半径较小时线路的初始弯曲矢度较大，在基本轨和护轨温度力共同作用下，轨道框架发生横向位移仍然较容易，但随着曲线半径的增大，线路初始弯曲矢度会急剧减小，Δtc提高量就会较大幅度增长;Δtc与曲线半径近似呈线性增长关系，当曲线半径为250～600 m时，对于50 kg/m钢轨护轨曲线半径每增大50 m，Δtc约提高4.7℃，对于60 kg/m钢轨护轨曲线半径每增大50 m，Δtc约提高4.9℃;同样曲线半径条件下，采用60 kg/m钢轨护轨比50 kg/m钢轨护轨的Δtc提高量要大;曲线半径为600 m的地段Δtc至少提高35.4℃，曲线半径大于600 m地段Δtc提高量将会更大，但是，可能没有实际意义。因为轨道结构可能受强度控制，稳定性将不起控制作用。

4.2 护轨横撑槽钢强度检算

在温度力作用下，护轨横撑槽钢中可能会有较大的内力，有必要对护轨横撑槽钢强度进行检算，不同曲线半径地段计算时提取护轨横撑槽钢内最大应力如表4和图6所示。

表4 护轨横撑槽钢最大应力Table 4 Maximal stress of U－steel

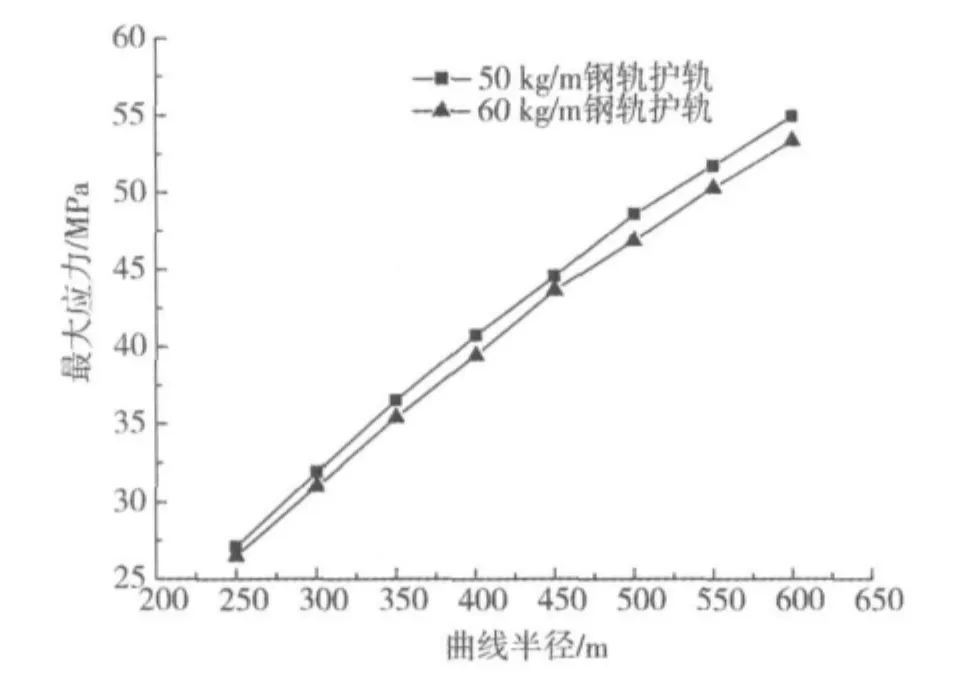
图6 护轨横撑槽钢最大应力与曲线半径关系Fig.6 Relationship between maximal stress of U －steel and curve radius

由表4和图6可知:随着曲线半径的增大，护轨横撑槽钢最大应力成增大趋势;在同样曲线半径条件下，采用60 kg/m钢轨护轨比50 kg/m钢轨护轨的横撑槽钢最大应力要小些，这与2种轨道框架刚度有差异有一定关系;当曲线半径为600 m时，护轨横撑槽钢最大应力仅为54.8 MPa，小于槽钢屈服强度235 MPa，槽钢强度能够满足要求。

5 结论

(1)护轨采用50 kg/m或60 kg/m的钢轨时，护轨中的最大温度力均为366.6 kN。

(2)考虑护轨作用的无缝线路稳定性分析表明，曲线半径小于600 m的地段，无缝线路的稳定性呈现不同程度的降低，按现有规范检算无缝线路稳定性是偏于不安全的。

(3)在本文的加强方案下，半径为250～600 m的小半径曲线地段的无缝线路的稳定性均能得到提高，且曲线半径越大，无缝线路稳定性的提高量越大，曲线半径为600 m的地段Δtc至少可提高35.4℃。

(4)加强方案下，护轨横撑槽钢的最大应力为54.8 MPa，其强度能够满足要求。

(5)采用60 kg/m钢轨护轨的对稳定性影响的效果要好于采用50 kg/m钢轨护轨。

(6)建议在进行小半径曲线桥上无缝线路稳定性检算时要考虑护轨的影响。

［1］广钟岩，高慧安.铁路无缝线路［M］.北京:中国铁道出版社，2005.GUANG Zhong-yan，GAO Hui-an.Continuously welded rail track［M］.Beijing:China Railway Publishing House，2005.

［2］铁道部工务局.铁路工务技术手册(轨道)［M］.北京:中国铁道出版社，1991.Ministry of Railway Works Bureau.Technical manual of railway works(Track)［M］.Beijing:China Railway Publishing House，1991.

［3］中铁工程设计咨询集团有限公司.新III型混凝土桥枕及护轨扣件(铺设图)［R］.北京:中铁工程设计咨询集团有限公司，2008.China Railway Engineering Consulting Group CO.LTD.New III type concrete sleeper and guard rail fastener(laying drawing)［R］.Beijing:China Railway Engineering Consulting Group Co.Ltd，2008.

［4］赵志军，陈秀方.无缝线路稳定性计算模型的研究［J］.长沙铁道学院学报，2001，19(3):31－36.ZHAO Zhi-jun，CHEN Xiu-fang.The new development for stability calculation model in CWR［J］.Journal of Changsha Railway University，2001，19(3):31 －36.

［5］曾志平.有限单元法在无缝线路稳定性计算中的应用［J］.石家庄铁道学院学报，2002，15(2):69－72.ZENG Zhi-ping.The application of finite element method in stability calculation ofCWR ［J］. Journalof Shijiazhuang Railway Institute，2002，12(2):69 －72.

［6］冯青松，宗德明，雷晓燕.无缝线路稳定性分析有限元模型［J］.中国铁道科学，2005，26(1):7－14.FENG Qing-song，ZONG De-ming，LEI Xiao-yan.Finite element model for analyzing the stability of continuously welded rail track［J］.China Railway Science，2005，26(1):7－14.

［7］刘 峰.无缝线路稳定性有限元分析［D］.北京:北京交通大学，2009.LIU Feng.Analysis of continues welded track stability based on finite element method［D］.Beijing:Beijing Jiaotong University，2009.

［8］李庆鸿，戴月辉，方永明.用荷载增量法求解无缝线路的稳定性［J］.上海铁道大学学报，1997，18(4):87－90.LI Qing-hong，DAI Yue-hui，FANG Yong-ming.Calculating the stability of jointless tracks with load increment method［J］.Journal of Shanghai Tiedao University，1997，18(4):87 －90.

［9］中华人民共和国铁道部.铁路无缝线路设计规范(送审稿)［S］.北京:中国铁道出版社，2007.Ministry of Railways of the People＇s Republic of China.Continuously welded rail track design code(approval review)［S］.Beijing:China Railway Publishing House，2007.

［10］中华人民共和国铁道部.新建铁路桥上无缝线路设计暂行规定［S］.北京:中国铁道出版社，2003.Ministry of Railways of the People＇s Republic of China.Temporary regulations of new continuously welded rail track design on bridge［S］.Beijing:China Railway Publishing House，2003.