铁路桥梁钢筋混凝土构件抗弯可靠度研究*

周慧芳，贡金鑫，张玉玲，刘晓光

(1.大连理工大学土木工程学院，辽宁 大连 116024;2.铁道科学研究院，北京 100081)

近年来，我国铁路工程高速发展，机车及相关的现代化设备不断更新，高速列车的运行速度已达300 km/h以上。然而，与此不相适应的是，我国铁路桥梁的设计方法多年来没有改进。从国际上看，工程结构设计正向概率极限设计方法方向发展，新近颁布的欧洲结构规范［1］(包括铁路桥梁设计)采用了概率极限状态设计体系;在美国，建筑规范［2］和公路桥梁规范［3］也采用了概率极限设计方法。对于铁路混凝土铁路桥梁，美国铁路工程师协会手册AREMA［4］提供了使用荷载设计法和荷载系数设计法2种方法。其中荷载系数设计法属于极限状态设计法，虽然荷载系数和抗力系数不是采用概率方法确定的，但不同荷载和不同的破坏方式荷载系数和抗力系数采用不同的值，概念上要比使用荷载法(相当于容许应力法)合理;20世纪90年代，我国建筑［5］、港口［6］、公路［7］和水利水电［8］工程结构也以相应的可靠度统一标准为基础，实现了由定值设计法向概率极限状态设计法的转轨;20世纪80年代，我国曾在铁路桥梁可靠度研究方面做了大量工作［9－13］，并编制了《铁路工程结构可靠度设计统一标准》［14］，但由于各种原因，铁路结构设计规范并没有在该标准的协调下完成由容许应力设计法或安全系数设计法向概率极限状态设计方法的过渡，只有《铁路隧道规范》［15］作为一种可选用方法提供了按概率极限状态进行设计的方法。迄今为止，我国铁路混凝土桥梁设计仍采用容许应力法，预应力混凝土桥梁设计采用安全系数法［16］。为推动铁路工程设计方法的全面发展，铁道部近期正在积极推动铁路工程结构概率极限状态设计方法的研究。本文对现行铁路混凝土桥梁规范中混凝土构件的抗弯可靠度进行分析。

1 现行铁路混凝土桥梁构件的抗弯设计方法

按照我国铁路铁路混凝土规范的规定，钢筋混凝土构件采用容许应力法设计。这时，混凝土应力按照三角形分布考虑，如图1所示，钢筋拉应力和混凝土外缘压应力应同时满足下列公式:

图1 我国规范采用的换算截面及应力分布Fig.1 Transformed section and stress distribution used in the specification

式中:M为荷载产生的弯矩;［σs］为构件钢筋容许应力;［σc］为构件混凝土容许应力;W0和Ws为混凝土受压边缘及对所验算的受拉钢筋中心处的换算截面抵抗矩;n为钢筋的弹性模量与混凝土的变形模量之比，即Es/Ec;k为截面混凝土受压区高度系数。

如图1所示，由截面力的平衡得:

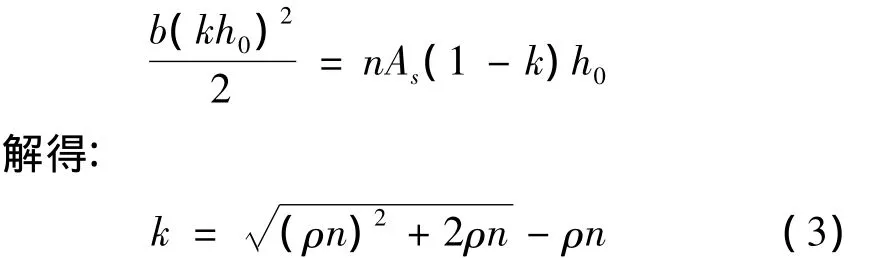
式中:ρ为受拉钢筋配筋率，ρ=As/(bh0)。

根据式(1)和式(2)，按容许应力法表示的抗弯承载力为下面两式中的小者:

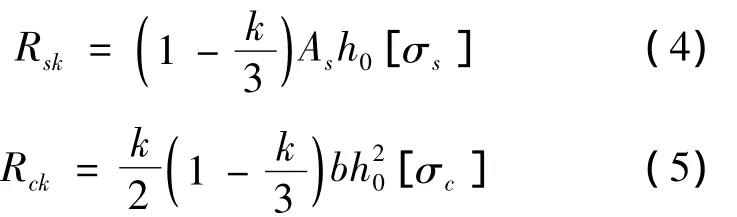
式中:Rsk为由钢筋容许应力确定的抗弯承载力;Rck为由混凝土容许应力确定的抗弯承载力。

式(4)与式(5)相比得:

2 极限状态和极限状态承载力

2.1 极限状态承载力

对结构进行极限状态设计，首先要明确结构的极限状态。按照《铁路工程结构可靠度设计统一标准》的规定，极限状态包括承载能力极限状态和正常使用极限状态。承载能力极限状态反映了结构或结构构件最终的破坏方式，统一标准给出了结构或结构构件达到极限状态的标志。对于钢筋混凝土构件的抗弯，极限状态是:(1)纵向受拉钢筋首先屈服，之后边缘受压混凝土达到极限压应变(适筋构件，图2(a));(2)纵向受拉钢筋未屈服而边缘受压混凝土先达到极限压应变(超筋构件，图2(b))。

图2 适筋梁和超筋梁的截面应变分布Fig.2 Strain distribution of under reinforced and over reinforced beams

钢筋混凝土受弯构件承载力的计算理论已经比较成熟，在建筑、公路桥梁、港工、水工等领域，尽管国内外规范采用的设计参数不同，但计算采用的模型基本是一致的，即在平截面假定的基础上，极限状态时将曲线受混凝土应力分布等效成矩形应力分布，如图2所示。对应于第1种极限状态的抗弯承载力计算公式为:

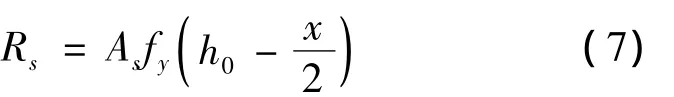
其中等效矩形应力的混凝土受压区高度x由下式确定:

由(8)解出x代入式(7)得:

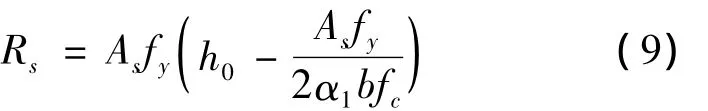
式中:As为受拉钢筋截面面积;fy为钢筋屈服强度;fc为混凝土抗压强度;h0为截面有效高度;b为构件宽度;α1为反映混凝土脆性的系数，按建筑规范，当混凝土等级不超过C50时，α1=1.0。

对于第2种极限状态，由于受拉钢筋未屈服边缘受压混凝土先压碎，属于无任何预兆的脆性破坏，按极限状态设计规范的规定不允许出现这种破坏方式。但现行的铁路混凝土桥梁规范采用仍容许应力设计法，容许应力方法只是设计采用的一种方法，按弹性状态考虑，材料达到规定的容许应力值并不代表结构会发生破坏，也不是按钢筋应力达到σs=［σs］设计构件就最终发生第1种方式的破坏，按混凝土应力达到σc=［σc］设计构件就最终发生第②种方式的破坏，也可能出现按钢筋应力达到σs=［σs］设计构件最终发生第2种方式的破坏，按混凝土应力达到σc=［σc］设计构件最终发生第1种方式的破坏。所以，研究按容许应力法设计的铁路混凝土桥梁可靠度时，必须考虑发生第2种破坏方式的情况。

发生第2种破坏方式时构件的抗弯承载力为

因为发生第2种破坏方式时钢筋未屈服，假定其应力为σs，根据截面力平衡和平截面假定得:

式中:ξ为混凝土相对受压区高度;Es为钢筋弹性模量;εcu为混凝土极限压应变，取0.003。所以，按照第2种破坏方式计算的构件抗弯承载力为:

2.2 极限状态方程

根据可靠度理论，铁路钢筋混凝土桥梁抗弯的极限状态方程可表示为［17］:

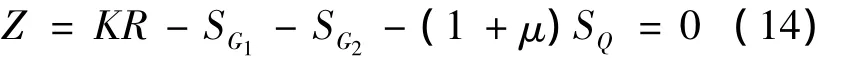
式中:R为抗力;K为R的计算模式不确定性系数;SG1为恒荷载效应;SG2为附加恒荷载效应;SQ为活荷载效应;1+μ为动力系数，根据文献按下式计算:

lp为跨度(m)。R为 Rs和 Rc中的小者，即 R=min(Rs，Rc)，所以，Z ＜0的事件等效于Zs＜0和Zc＜0两者之一发生的事件，即Zs＜0∪Zc＜0，其中

式中:Ks为以受拉钢筋先屈服之后混凝土压碎为破坏特征的承载力计算模式不确定性系数;Kc为以受压混凝土先压碎为破坏特征的承载力计算模式不确定性系数。

按Zs＜0∪Zc＜0计算构件的失效概率可采用结构体系可靠度分析方法［18］，需要计算Zs与Zc间的相关系数，比较复杂。为简化计算，本文以对应于Zs与Zc的可靠指标的较小值作为构件的可靠指标。

3 基本变量的统计参数

进行可靠度分析，需要知道基本随机变量的统计参数和概率分布。在式(14)中，根据文献恒荷载、附加恒荷载和活荷载的统计参数和概率分布类型如表1所示，这些荷载的统计参数是用其平均值与标准值的比值和变异系数表示的，这样表示的目的反映的是荷载偏离其标准值的统计规律，同时也建立了荷载的统计参数与设计中其标准值的关系。

表1 变量参数Table 1 Parameters of the variables

对于式(14)中构件的抗弯承载力为R，可靠度分析中其统计参数也同样表示为平均值与标准值的比值kR=μR/Rk和变异系数δR的形式，但这里抗力随机变量有Rs(式(9))和Rc(式(13))2种表达式，抗力标准值有Rsk(式(4))和Rck(式(5))2种表达式，这样计算的抗力统计参数有表2中的4种组合，这4种组合表示了对应于不同的设计，构件实际可能发生的情况。存在这4种情况是因为现行铁路桥梁设计规范采用的是容许应力设计法，按容许应力设计法实际的构件达到容许的钢筋应力，并不意味着极限状态破坏是时钢筋屈服，对于混凝土也是如此。

表2 计算抗力统计参数的4种组合Table 2 The 4 combinations for resistance parameters calculation

按照表2中的抗力组合和表1中的统计参数，可按文献［17］根据基本随机变量的统计参数近似确定综合随机变量的统计参数，表3所示为构件抗力的均值系数和变异系数。

表3 基本随机变量的统计参数和概率分布Table 3 The parameters and distribution of the basic random variables

4 可靠指标计算

根据式(14)表示的极限状态方程和表4中的抗力统计参数，可计算钢筋混凝土桥梁抗弯承载力的可靠指标。根据表1，活荷载效应的平均值和标准差为:

假定恒荷载效应与活荷载效应标准值的比值为λ1，附加恒荷载效应与活荷载效应标准值的比值为λ2，则根据表1，恒荷载效应和附加恒荷载效应的平均值和标准差为:

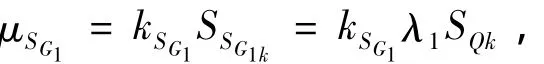
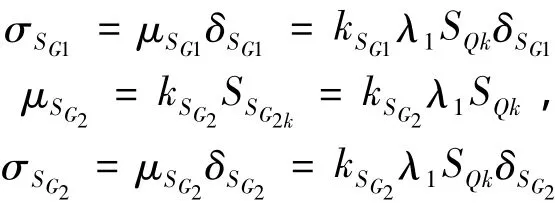
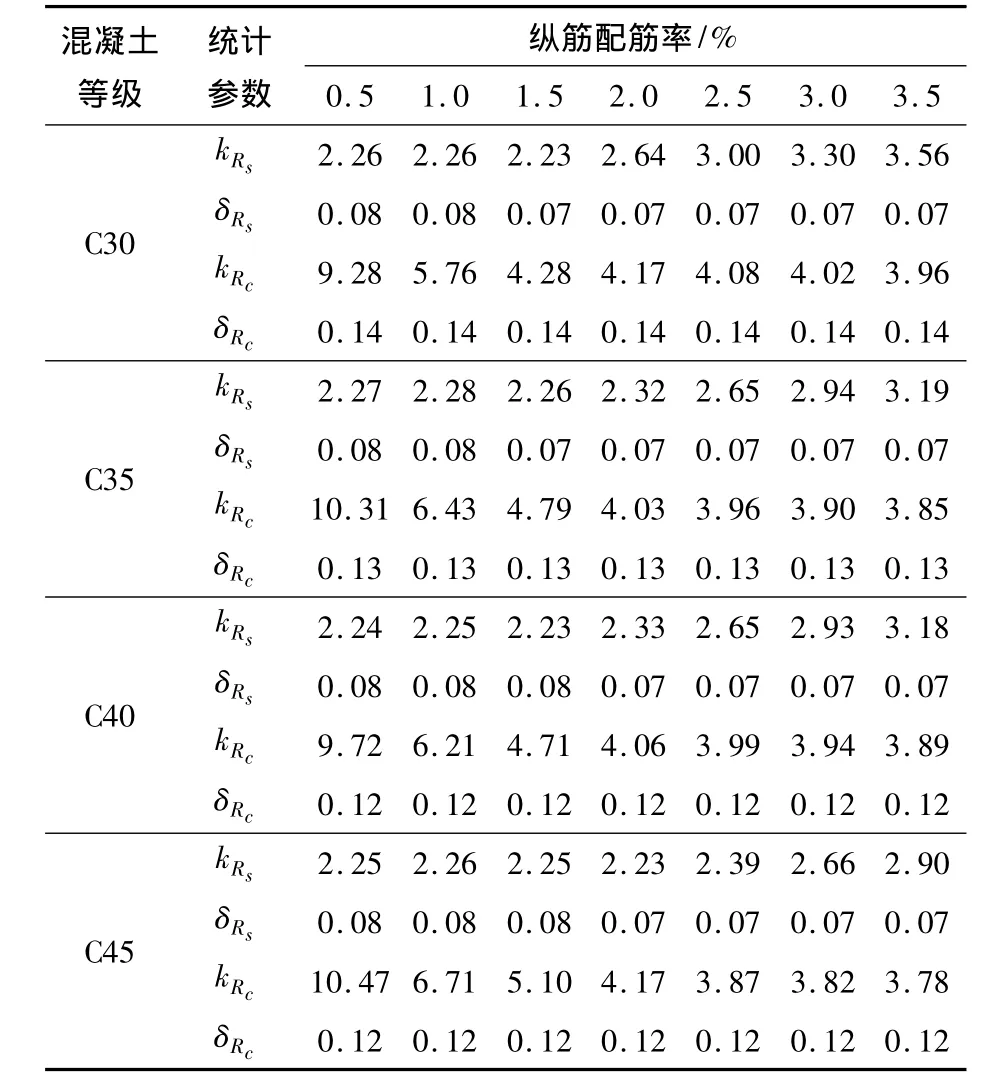
表4 统计参数Table 4 Statistical parameters

构件可能发生受拉钢筋屈服和受压混凝土压碎两种形式的破坏，式(14)中的抗力可表示为R=min(Rs，Rc)，其中Rs的平均值和标准差为:

对于铁路钢筋混凝土桥梁，一般情况下，恒荷载与活荷载的比值为0.2～1，恒荷载与附加恒荷载的比值在2～4的范围内。本文分析中恒荷载与活荷载的比值取为λ1=0.75，附加恒荷载与活荷载的比值取为λ2=0.25，跨度取为lp=30 m时，图3所示为结构构件可靠指标随配筋率的变化，其中实线为构件极限承载力由钢筋屈服控制的情况，虚线为构件极限承载力由混凝土压碎控制的情况。由图3可以看出:①2种情况下可靠指标随配筋率的变化形式是不同的，构件极限承载力由钢筋屈服控制情况的可靠指标随配筋率增大而降低，构件极限承载力由混凝土压碎控制情况的可靠指标随配筋率增大而增大，2条曲线明显的转折点对应于容许应力法设计中构件受［σs］控制和受［σc］控制的临界配筋率ρ0。需要说明的是，这里分析的构件可靠指标是按规范公式(本文式(4)和式(5))设计的构件的可靠指标，这时的配筋率与荷载有关，与一个荷载不变的具体构件不是一个概念。对于一个荷载不变的具体构件，提高构件的配筋率，可靠指标应是增大的。②混凝土强度等级对按规范公式设计的构件的可靠指标影响不大。这种情况与单个具体构件可靠指标的情况相比，同配筋率影响的情况相似。③按照本文前面的说明，本文取两者情况的最小可靠指标作为铁路钢筋混凝土桥梁按规范公式设计时的可靠指标，基本为5.8 ～6.5。

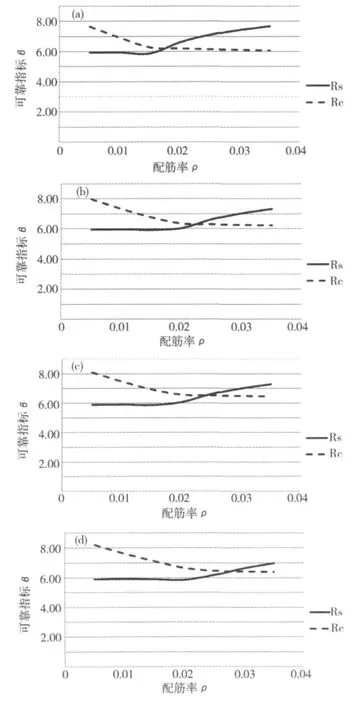
图3 可靠指标随配筋率的变化Fig.3 Relationship between reliability index and reinforcement ratio

图4所示为跨度30 m、配筋率为2%时铁路钢筋混凝土桥梁可靠指标随恒荷载与活荷载效应标准值比值的变化。由图4可以看出:①随恒荷载与活荷载效应标准值之比的增大，可靠指标减小，但变化不大。②对于混凝土强度等级为C30的情况，构件的可靠度由混凝土先压碎的状态控制;对于混凝土强度等级为C35，C40和C45的情况，构件的可靠度由钢筋先屈服、混凝土后压碎的状态控制。

图4 可靠指标随c的变化Fig.4 Relationship between reliability index and reinforcement ratio

5 结论

(1)取决于受拉钢筋的配筋率，铁路钢筋混凝土桥梁可能发生钢筋先屈服而后混凝土压碎的破坏和钢筋未屈服混凝土先压碎的破坏方式。

(2)按铁路桥涵设计规范 TB 10002.3—2005的容许应力法设计的铁路钢筋混凝土桥梁受弯构件承载力可靠指标为5.8～6.5。

［1］BS EN 1992 －2:2005，Eurocode2:Design of concrete structures－part 2:Concrete bridges－design and detailing rules［S］.

［2］ACI 318—08，Building code requirements for structural concrete and commentary［S］.

［3］AASHTO，AASHTO lrfd bridge design specification［S］.

［4］American Railway Engineering and Maintenance－of－Way Association AREMA Manual for Railway Engineering［S］.

［5］GB 50068—2001，建筑结构可靠度设计统一标准［S］.GB 50068—2001，Unified design standard for reliability of building structure［S］.

［6］GB 50158—2010，港口工程结构可靠性设计统一标准［S］.GB 50158—2010，Unified standard for reliability design of port engineering structures［S］.

［7］GB/T 50283—1999，公路工程结构可靠度设计统一标准［S］.GB/T 50283—1999，Unified standard for reliability design of highway engineering structures［S］.

［8］GB 50199—94，水利水电工程结构可靠度设计统一标准［S］.GB 50199—94，Unified design standard for reliability of hydraulic engineering structure［S］.

［9］姜昭恒，陈晓天.铁路混凝土桥梁强度可靠性研究［J］.长沙铁道学院学报，1991，9(3):111－120.JIANG Zhao-heng，CHEN Xiao-tian.Research of the strength reliability of railway concrete bridge［J］.Journal of Changsha Railway University，1991，9(3):111 －120.

［10］文雨松.铁路混凝土T形梁多表达式极限状态的可靠指标［J］.长沙铁道学院学报，1990，8(2):49－54.WEN Yu-song.Reliability of railway concrete T－beam with multi－ limit state function［J］.Journal of Changsha Railway University，1990，8(2):49－54.

［11］文雨松.铁路混凝土桥梁梁体自重的概率分析及标准值［J］.长沙铁道学院学报，1989，7(2):46－48.WEN Yu-song.Probability analyses of the weight of concrete railway bridge and its nominal value［J］.Journal of Changsha Railway University，1989，7(2):46－48.

［12］文雨松，江继军，危永强.铁路桥梁桥上永久作用的试验研究［J］.长沙铁道学院学报，1990，8(4):77－83.WEN Yu-song，JIANG Ji-jun，WEI Yong-qiang.An experimental investigation on dead loads acting on railway bridges［J］.Journal of Changsha Railway University，1990，8(4):77－83.

［13］李亚东.铁路桥梁的可靠度评估［J］.西南交通大学学报，1993(6):75－83.LI Ya-dong.Reliability evalution of railway bridge［J］.Journal of Southwest Jiaotong University，1993(6):75－83.

［14］GB 50216—1994，铁路工程结构可靠度设计统一标准［S］.GB 50216—1994，Unified design standard for reliability of railway engineering structures［S］.

［15］TB 10003—2005，铁路隧道设计规范［S］.TB 10003—2005，Code for design on tunnel of railway［S］.

［16］TB 10002.3—2005，铁路桥涵钢筋混凝土和预应力混凝土结构设计规范［S］.TB 10002.3—2005，Code for design on reinforced and prestressed concrete structure of railway bridge and culvert［S］.

［17］李铁夫.铁路桥梁可靠度设计［M］.北京:中国铁道出版社，2006.LI Tie-fu.Design on reliability for railway bridge［M］.Beijing:China Railway Publishing House，2006.

［18］贡金鑫，魏巍巍.工程结构可靠性设计原理［M］.北京:机械工业出版社，2007.GONG Jin-xin，WEI Wei-wei.Principle of reliability design for engineering structures［M］.Beijing:China Machine Press，2007.