拱肋内倾角对钢管混凝土提篮拱桥车桥动力响应的影响*

王 柳，彭荣华，郭向荣

(中南大学土木工程学院，湖南 长沙 410075)

钢管混凝土拱桥是一种由混凝土和钢材2种材料组合而成的新型桥型，近年来，钢管混凝土拱桥在我国公路和城市桥梁建设中得到迅速发展，并逐步推广到铁路及城市轻轨交通中。它利用钢管和混凝土2种材料在受力过程中的相互作用，使混凝土的强度提高，塑性和韧性也大为提高;同时，混凝土的存在也使得钢管避免或延缓发生局部屈曲，可以保证其材料性能的充分发挥［1－2］。随着钢管混凝土拱桥跨径的增大，其横向稳定的问题变得比较突出，尤其是宽跨比较小的情况下，一般可以采用拱肋内倾的方式，即采用提篮拱的形式来提高整体横向稳定性［3－4］。目前，国内很多学者对钢管混凝土提篮拱桥的力学性能进行了研究，在静力学方面，文献［5－7］对该类桥梁的稳定性和极限承载力的影响进行了大量的研究;在动力学方面，文献［8－9］分别分析了该类桥型的自振特性和抗震性能。研究表明，钢管混凝土提篮拱桥应用于高速铁路桥梁中，有着较好的动力性能和行车舒适度［10－12］。目前，国内外关于拱肋内倾角对该类桥梁的动力特性及车桥动力响应的影响研究较少，研究内倾角变化引起的提篮拱桥车桥响应的变化规律有助于该类桥型的研究。目前，我国已有多座钢管混凝土拱桥处于设计施工阶段，研究钢管混凝土提篮拱内倾角变化对车桥动力响应的影响有一定的工程意义。本文作者以某大跨度钢管混凝土提篮拱桥为工程背景，对比了3种不同拱肋内倾角下的结构动力特性，并进行车桥耦合振动分析，讨论拱肋内倾角对桥梁动力响应、车辆安全性及舒适性的影响。

1 工程概况

某上承式钢管混凝土拱桥，总体布置图如图1所示。下部拱的跨径为240 m，拱肋轴线矢高58 m，矢跨比约为1/4.14，拱轴系数3.2。拱肋由4根φ1100 mm钢管组成，拱肋外边缘宽度为3.0 m，高度为5.7 m，其上、下弦各由两肢钢管与其间的钢板连接而呈哑铃形，上下弦钢管和钢板围成的空腔内均灌注C50微膨胀膨胀混凝土，上、下之间用工字钢板连接成为桁架形式。从拱趾起两跨21.15 m梁范围内，上下弦之间采用实腹板，每块实腹板由两块钢板及内填的C50微膨胀混凝土构成。拱上桥面结构采用3联4×21.15 m钢—混凝土连续结合梁，桥梁全长为494.68 m。图2所示为此文结合梁截面图，图3所示为拱肋典型截面构造图。桥梁的二恒取173 kN/m，设计速度为250 km/h客运专线，双线行车，线间距为5 m。

图1 桥梁结构总体布置图Fig.1 Overall arrangement of bridge structure

2 结构动力特性分析

2.1 桥梁有限元模型

为考查内倾角对结构动力特性的影响，采用有限元软件分别计算了内倾角为 7.5°，8.5°和 9.5°情况下的动力特性。在横向风及偏心车辆的作用下，桥梁结构会在横向、竖向、纵向发生静力变形和动力响应，因此，必须建立能够反映结构动力效应的三维有限元模型。本算例中拱肋、拱肋间联结系，拱上立柱以及主梁工字梁均采用空间梁元模拟，混凝土桥面板采用板单元模拟，钢材及混凝土弹性模量E和泊松比μ按现行桥规取值。为了更好地反映拱肋内倾角对提篮拱动力性能的影响，对模型有以下基本假定:(1)变化倾角时，横桥向两拱脚之间的距离保持不变;(2)拱肋间的横向联系方式不变，仅在宽度方面随肋间距离同时变化;(3)边界条件保持一致。桥梁三维有限元划分如图4所示。

图2 结合梁横截面图Fig.2 Cross section of composite beam

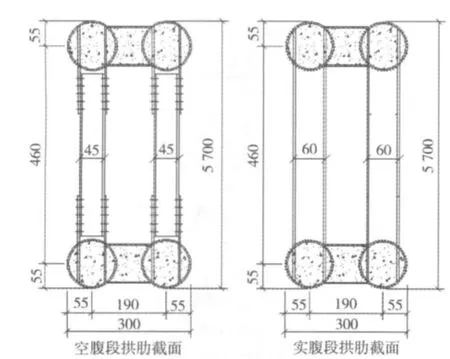
图3 拱肋典型截面构造图Fig.3 Typical section of arch rib

图4 有限元划分示意图Fig.4 Finite element model of the bridge

2.2 自振频率分析

按上述有限元模型，计算得到3种不同内倾角下结构自振频率的对比，如表1所示。图5所示为内倾角为7.5°时桥梁的第一阶横向、竖向和纵向振型图。

由表1可见:3种不同的拱肋内倾角度下，结构的横向自振频率随着内倾角的增大而增大，内倾角为8.5°和9.5°的横向自振频率增幅分别为9%和15%，竖向自振振动频率随内倾角度的增大而稍有减小，变化幅度没有横向频率显著，表明钢管提篮拱桥随着拱肋内倾角的增大，拱肋的横向刚度随之增大，而面内的竖向刚度却略有减小。纵向自振频率随内倾角的变化不是很明显，基本没有变化，主要原因是结构纵向支承体系未发生变化，横向刚度对纵向振动的影响较小。关于拱肋内倾角的变化对钢管提篮拱桥自振频率的影响，文献［13－14］的研究结论与本文基本一致。文献［13］指出:内倾角的变化对钢管混凝土提篮拱桥的横向刚度影响较为明显，其竖向刚度影响相对较小;文献［14］亦得出:涉及面外振动的振型所对应的频率随着内倾角的增大而增大，但拱梁面内振动对应的频率却是随着内倾角的增大而减小，但是频率减小很小。

表1 不同内倾角结构自振频率对比Table 1 Comparison of structural natural vibration characteristics of different leaning angle Hz

图5 7.5°时第1阶横向振型Fig.5 The 1st lateral vibration mode(7.5°)

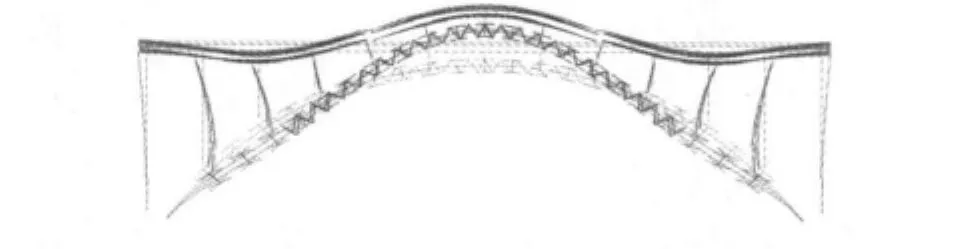
图6 7.5°时第1阶竖向振型Fig.6 The 1st vertical vibration mode at 7.5°

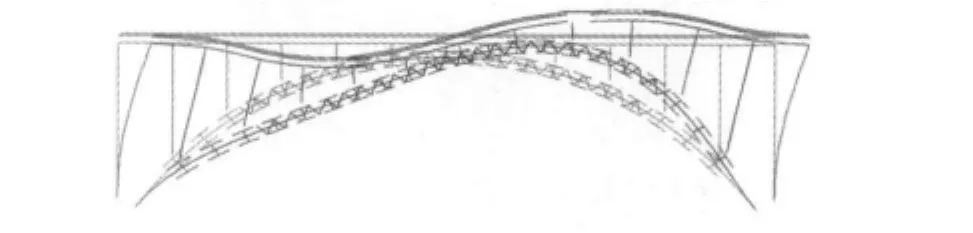
图7 7.5°时第1阶纵向振型Fig.7 The 1st longitudinal vibration mode at 7.5°

3 车桥耦合振动分析

3.1 空间振动方程的建立与求解

本文在研究空间振动方程时，首先运用达朗伯原理建立车桥系统运动方程，将列车与桥梁视为为一个耦合的整体体系，然后采用曾庆元院士提出的“动力学势能不变值原理”［15］与形成矩阵的“对号入座”［16］法则建立桥梁刚度、质量、阻尼等矩阵，形成系统的空间振动矩阵方程:

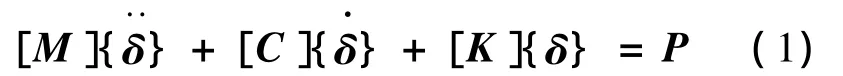
根据前述计算模型与计算原理对列车—桥梁时变系统空间振动响应进行了计算，本文采用的计算车辆为国产CRH2型客车，列车编组为“动车+拖车+拖车+动车+动车+拖车+拖车+动车”，速度等级取160～300 km/h，轨道不平顺采用德国低干扰轨道谱。采用中南大学自主研发的列车桥梁时变系统空间振动分析软件TBI，进行车桥耦合振动分析。

3.2 桥梁空间动力响应

为了体现拱肋内倾角对车桥动力响应中桥梁响应的影响，表2所示为不同内倾角度下CRH2列车以速度250 km/h通过桥梁时桥梁的动力响应值。由表2可以看出:3中内倾角度下拱顶竖向位移和加速度的变化很小，而横向位移、横向加速度均随着内倾角度的增大而减小，可见，桥梁的横向响应对拱肋内倾角的变化较为敏感。

图8和图9所示分别为CRH2列车以250 km/h的速度通过不同拱肋内倾角下时拱顶横向位移和竖向位移的时程曲线。

3.3 列车空间动力响应

表3所示为列车以250 km/h的速度通过桥梁时的车辆响应计算结果。由表3可见:3种不同内倾角下车辆各项动力响应变化不明显;从整体上来看，内倾角为7.5°时的动车和拖车的动力响应较其他2种情况下略大，其中横向加速度和横向舒适度指标变化较大，在8.5°和9.5°2种情况下车辆动力响应基本保持不变，表明拱肋内倾角的变化对车辆横向动力响应有一定的影响，但总体来说不是很明显。

表2 车速为250 km/h时不同拱肋内倾角度下桥梁动力响应Table 2 Bridge dynamic responses under different leaning angle when train speed is 250 km/h

图8 250 km/h时拱顶横向位移时程曲线Fig.8 Time history curves of vault lateral displacement at train speed of 250 km/h

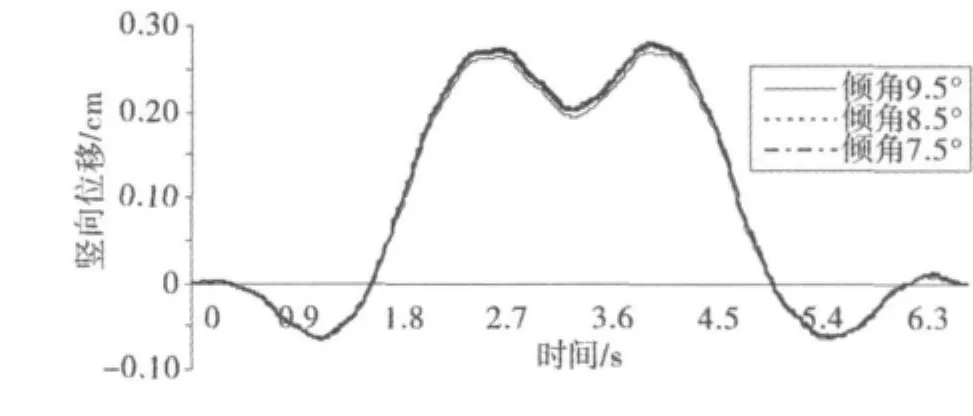
图9 250 km/h时拱顶竖向位移时程曲线Fig.9 Time history curves of vault vertical displacement at train speed of 250 km/h

表3 车速为250 km/h时不同拱肋内倾角度下车辆动力响应Table 3 Train dynamic responses under different leaning angle when train speed is 250 km/h

4 结论

(1)横向振动频率随拱肋内倾角的增加而明显增大;竖向自振振动频率随内倾角度的增大而减小，变化幅度没有横向频率显著;纵向自振频率随内倾角的变化不是很明显。

(2)不同内倾角度下桥梁拱顶竖向位移和加速度的变化很小，而横向位移、横向加速度均随着内倾角度的增大而减小。

(3)3种内倾角下车辆响应变化不明显，内倾角为7.5°时的动车和拖车的动力响应比其他2种情况下略大，车辆的响应对内倾角的变化不敏感。

［1］陈宝春.钢管混凝土拱桥发展综述［J］.桥梁建设，1997(2):8－13.CHEN Bao-chun.A summarized account of developments in concrete － filled steel tube arch bridge［J］.Bridge Construction，1997(2):8 －13.

［2］黄平明，任 翔，李文杰.拱肋内倾角对钢管混凝土拱桥静动力学的影响［J］.长安大学学报:自然科学版，2009，29(2):51 －54.HUANG Ping-ming，REN Xiang，LI Wen-jie.Influence of leaning angle of arch rib on concrete－filled－steeltube arch bridges static and dynamic mechanics properties［J］.Journal of Chang’an University:Natural Science E-dition，2009，29(2):51 －54.

［3］陈宝春.钢管混凝土拱桥设计与施工［M］.北京:人民交通出版社，1999.CHEN Bao-chun.Design and construction of concretefilled steel tube arch bridge［M］.Beijing:People’s Communications Press，1999.

［4］金伟良.大跨度拱桥的横向稳定性分析［D］.大连:大连理工大学，1988.JIN Wei-liang.Lateral stability analysis of big span arch bridge［D］.Dalian:Dalian University of Technology，1988.

［5］陈宝春.钢管混凝土拱桥计算理论研究进展［J］.土木工程学报，2003，36(12):47 －55.CHEN Bao-chun.State of the art theory and calculation for concrete － filled steel tube arch bridge［J］.China Civil Engineering Journal，2003，36(12):47 －55.

［6］刘 芳.下承式钢管混凝土拱桥空间稳定性与极限承载力研究［D］.长沙:中南大学，2008.LIU Fang.Stability and ultimate bearing capacity analysis of bottom－through concrete－filled steel tube arch bridge［D］.Changsha:Central south university，2008.

［7］陈宝春，陈友杰.钢管混凝土肋拱面内受力全过程试验研究［J］.工程力学，2000，17(2):44 －50.CHEN Bao-chun，CHEN You-jie.Experimental study on mechanic behaviors of concrete－filled steel tubular archunder in － plane loads［J］.Engineering Mechanics，2000，17(2):44－50.

［8］陈 淮，朱 倩，葛素娟，等.韩江北桥主桥动力特性研究［J］.铁道科学与工程学报，2005，2(5):28 －31.CHEN Huai，ZHU Qian，GE Su-juan，et al.Dynamic characteristics analysis of Hanjiang Northen Bridge［J］.Journal of Railway Science and Engineering，2005，2(5):28－31.

［9］熊 峰.钢管混凝土拱桥抗震性能研究［D］.成都:四川大学，2001.XIONG Feng.Study on seismic behavior of concrete －filled steel tube arch bridge［D］.Chengdu:Sichuan University，2001.

［10］单德山，李 乔.铁路提篮拱桥车桥耦合振动分析［J］.西南交通大学学报，2005，40，(1):53 －57.SHAN De-shan，LI Qiao.Coupled vibration analysis of X － style arch bridge and vehicles［J］.Journal of Southwest Jiaotong University，2005，40，(1):53 －57.

［11］周智辉，向 俊，曾庆元.客运专线某钢管混凝土提篮拱桥列车走行性分析［J］.铁道科学与工程学报，2008，5(1):46 －50.ZHOU Zhi-hui，XIANG Jun，ZENG Qing-yuan.Analysis of train running performance on a basket handle arch bridge of concrete－filled steel tube on passenger special line［J］.Journal of Railway Science and Engineering，2008，5(1):46 －50.

［12］罗 浩，郭向荣.大跨度提篮拱桥车桥耦合振动分析［J］.振动与冲击，2008，27(2):147 －149.LUO Hao，GUO Xiang-rong.Coupled vibration analysis of big span X － style arch bridge and vehicles［J］.Journal of Vibration and Shock，2008，27(2):147 －149.

［13］耿 飞.大跨度钢管混凝土拱桥动力特性分析［D］.西安:长安大学，2010.GENG Fei.Dynamic behavioral analysis of long－ span concrete filled steel tubular arch bridges［D］.Xi’an:Chang’an University，2010.

［14］任 翔，许汉铮.钢管混凝土提篮式拱桥动力特性及参数敏感性分析［J］.公路，2008(4):78－83.REN Xiang，XU Han-zheng.Dynamic behavior and parameter sensitivity analysis of concrete filled steel tubular arch bridge［J］.Highway，2008(4):78 －83.

［15］曾庆元，郭向荣.列车桥梁时变系统振动分析理论与应用［M］.北京:中国铁道出版社，1999.ZENG Qing-yuan，GUO Xiang-rong.Theory and application of train－bridge time－variant system vibration analysis［M］.Beijing:China Railway Press，1999.

［16］曾庆元，杨 平.形成矩阵的“对号入座”法则与桁段有限元法［J］.铁道学报，1986，8(2):48 －59.ZENG Qing-yuan，YANG Ping.The“set－ in － rightposition”rule for formulating matrix and the truss finite element method for spatial truss analysis［J］.Journal of the Railway Society，1986，8(2):48 －59.