基于3D混合树和视觉特性的视频可分级编码算法

付明哲，王相海,2，宋传鸣

（1. 辽宁师范大学 计算机与信息技术学院，辽宁 大连 116029；2. 智能计算与信息处理教育部重点实验室，湖南 湘潭 411105）

1 引言

网络及移动计算技术的稳步发展使用户可通过多种接入设备实时访问网络视频资源。然而在视频传输过程中，对用户所提出的不同要求和终端性能的差异、网络异构特性所带来的各支路服务能力的差异以及网络拥塞和噪声等影响传输的因素等使得对视频信息的多质量服务需求急剧增加，这样对视频压缩编码技术的新需求——可分级编码便成为了一个热点问题[1,2]。近年来，小波在图像编码方面的巨大成功使人们转去思考基于小波的视频可分级编码问题，出现了2类基于小波的视频可分机编码方法[3]，一类是基于运动补偿的 2D小波视频编码方法，该类方法的难点是如何有效地实现小波域帧间运动估计，避免误差“漂移”问题的产生；另一类是基于 3D小波视频编码方法[4]，该类方案以其无块效应和可分级特性的易于实现而受到关注[5～8],然而由于在时间维的滤波一般并不与视频对象的运动方向相一致，这样通常会影响时间域冗余的去除，编码效率不是很高。JVT也曾在 2004年成立了一个特别研究组来探索基于小波的更高效率的编码[9]，并进一步支持除可分级编码外的其他特性[10]，如视频高分辨率存储与传输和极细粒度的信噪比可分级等。总之，基于小波的视频可分级编码技术还处于不断发展中，很多问题还有待进一步研究[11]。

本文首先对视频3D小波系数的分布特性进行了分析，提出了一种混合的3D空间树结构，并结合 HVS对各子带敏感程度的差异，给出了一个子带系数加权方案，进一步提出本文的视频编码架构，架构充分利用了视频3D小波变换后时间域低频帧与高频帧的系数分布特点，根据尺度间和尺度内小波系数幅值相关性，在时间域低频子带和高频子带分别采用相应的系数结构来组织重要系数的编码，从而使得幅值较大的系数排在码流前端，提高了编码效率，特别对较低码率情况。

2 相关工作分析

对视频小波系数进行可分级编码需要解决的一个重要问题是如何对重要系数进行定位。早期方案大都采用树型结构[12,13]对时间域滤波后的系数进行组织，这种树型对时间域低、高频系数的组织具有相同的结构。但从文献[11]的研究可以看出，视频在空间和时间维所具有的相关性不尽相同，并且通常会存在较大的差异，时间维的相关性往往要大于空间维的相关性，这样时间维的高频系数幅值一般要小于空间维的高频系数。可见这种传统对称树型结构一般不利于大幅值重要系数的前置，将会对编码效率产生影响，特别是对中、低码率的编码。文献[5]采用了一种近似对称的空间方向树，获得了高于对称树结构的编码效率，但它要求时、空方向的小波分解级数必须相同，这不利于发掘不同方向的系数相关性；文献[14]改进了 3D-SPIHT的空间方向树，将时间低频帧中空间低频的部分系数与前一粗尺度下的高频帧系数建立了关联，对时间维的低频系数和空间维的高频系数进行优先编码，但由于该方法没有考虑高频系数相关性较低这一特点，会在一定程度上影响时间高频帧的编码效率；文献[15]以零树为基础建立了一种非对称树结构，将那些对父节点具有较高依赖程度的时空系数置于同一层，与对称的树结构相比，该结构有利于零树包含更多系数，在一定程度上改进了编码效率；文献[6,16]提出了“虚拟树”的概念，即在构造树结构时假定最低频子带又进行了一次小波分解，从而增加分解层次来使一棵树包含更多系数，但仍然忽略了位于同一层零树上时空系数成为重要系数的概率不同的事实，其编码效率尚有提高空间；文献[17]从时空系数相关性不一致出发，将时空方向树分解为时间方向树和空间方向树，并优先处理前者。只有当时间方向树的某个系数为重要系数时，才去扫描该系数所在的空间方向树，但该方案会推迟对空间方向树中孤独零的处理；文献[18]在零树的基础上，将亮度分量作为色度分量的父亲，以增加树结构的长度，在低码率下提高了编码效率。文献[19]在充分考虑几种基本树结构的基础上，将“零块”思想引入其中，以挖掘系数的子带内相关性，但其同一层系数成为重要系数的概率不同这一事实仍然存在。总之，现有算法对各子带大幅值系数的同等对待忽略了这些系数对重构视频质量的差异，不利于提高视频解码的主观质量。

3 3D混合树结构的提出

3.1 小波变换系数的相关性分析

对基于树结构的编码方案，不同子带系数的相关性是设计树形结构的重要依据[15]。

记 (,)p x y为视频帧中(,)x y位置的灰度值，则2像素的自相关函数 (,)r m n定义为

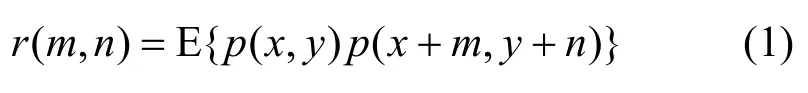
其中，m, n∈ℤ，E{·}为数学期望。电视画面的自相关系数一般在0.95至0.98之间[20]。

对于 l( l ≥ 1) 级的视频帧小波变换，2个变换系数间的自相关函数为[11]

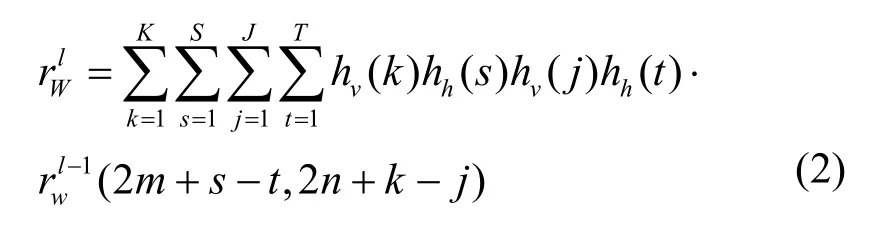
其中， hh和 hv分别表示2D小波变换水平和竖直方向的滤波器，K和J为 hv的长度，S和T为 hh的长度， rW0(m, n ) = r ( m, n)。

对于低频子带(LL)，其自相关函数为

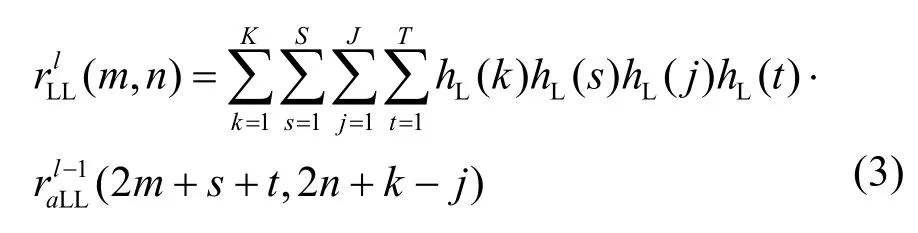
对于高频子带 B ∈ ｛ H L ,LH,HH｝，自相关函数为

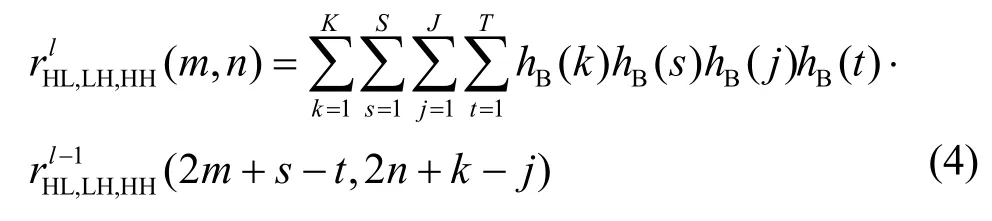
依据低通和高通以及水平和竖直高通2对滤波器间的正交性，有

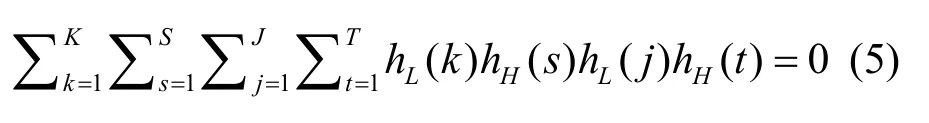
3.2 时、空方向树混合结构

3.2.1 传统树形结构分析

图像编码的EZW[12]和SPIHT算法[13]的核心是采用如图1所给出的零树来组织图像的小波系数，其中，EZW零树基于尺度间系数幅值的衰减来关联父子带与孩子子带间的系数；SPIHT零树则在此基础上增加了对相邻系数所具有相关属性的考虑。由前一节知道，时域低频与空域低频子带的相邻系数间的相关性较高，如果直接采用EZW树结构来对系数进行组织，这种系数间的相关特性将会被忽略掉，同时会较SPIHT零树增加更多的同步信息；此外，对于相关性较低的高频系数（尽管如此，这些高频系数仍将会近似满足尺度间幅值的衰减特性，如图 1(b)中的白、灰色像素)，若采用 SPIHT树结构来对高频系数进行组织，其父系数(参见图 1(b)所示LL中的黑色像素)及对应的子带中的系数可能不会构成零树，这是由于此时可能会错过诸如EZW树结构中相应的节点，进而 “孤立点”的数量将大幅增加，势必会影响最后的编码效率。对于通过MCTF所产生的帧差，通常其高频系数的相关性会更低。总之，单一的树形结构很难同时有效地兼顾时间域低、高频帧的系数分布情况，难以提高整体编码效率。

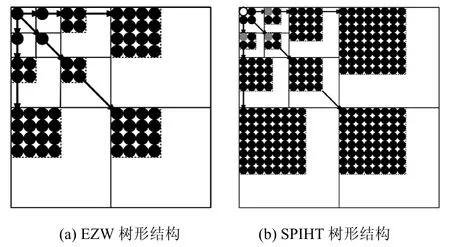
图1 2D情况下的2种树结构

3.2.2 混合树形结构

本文提出一种混合时空方向树结构，图2为4帧情况的示意，其中在时间域上进行了2级滤波，空间域为1级，箭头经父节点至子节点，父子关系由不同尺度子带中的相同字母来表示，而兄弟关系则由同尺度的相同字母来表示。

提出树形结构的内部构成：1）时间域低、高频帧分别采用SPIHT树形结构和EZW树形结构；2）由于经 MCTF处理后的视频帧的能量主要集中在时间低频帧，这样只将时间低频帧中空间LL子带与时间高频帧中子带构成父子关系，这样时间低频与空间高频子带中的系数势必会得以优先编码；3）由于时间高频帧中的信息主要是由运动补偿的误差所引起的，这样运动物体的边缘上将会聚集主要的能量，可见时域高频与低频帧系数的分布是不同的，时间高频帧的空间高频子带将会出现较大的幅值系数，通常具有更高比例的能量。这样，提出的混合树形结构将时域高频帧的空间 LL系数与时域更高频帧对应的子带系数构建父子关系，即将空域高、低频系数同等看待，这将会使物体边缘的大幅值系数编码的优先级得以提高。

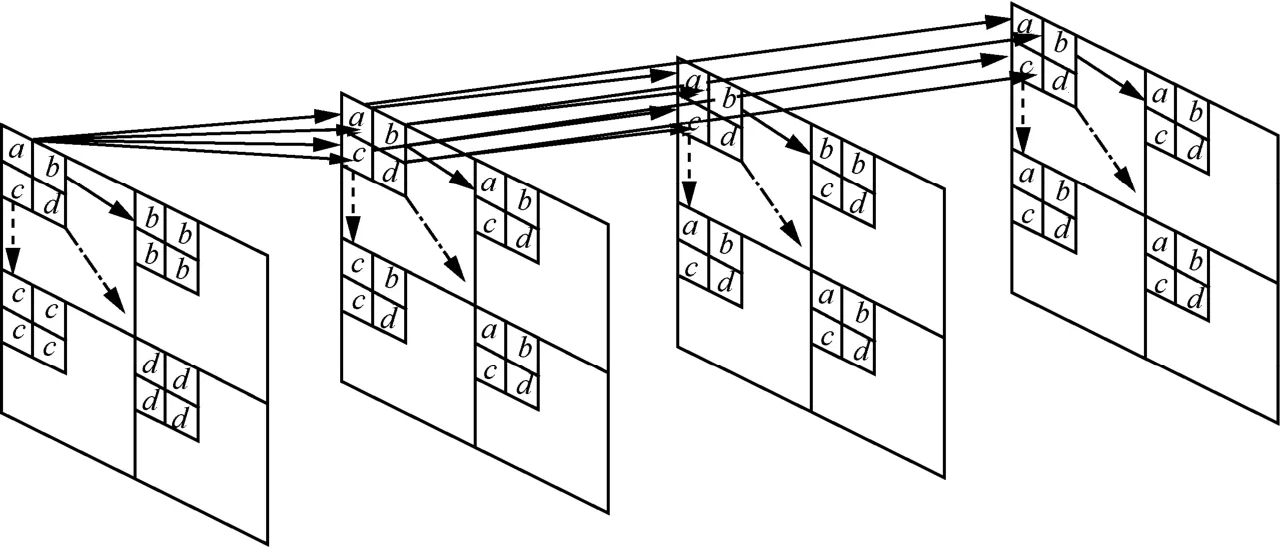
图2 时、空混合方向树

4 基于HVS特性的小波系数加权

HVS对信号频率的敏感程度是不同的[21]，一般而言，对于高、中、低3个频率分量，HVS对中频会更加敏感一些。此外，对于方向不同的频率分量也会表现出一定不同的敏感程度，通常 HVS对竖直和水平方向的频率会较对角线方向的频率更加敏感。而对于图像及视频，若使 HVS敏感的频率系数优先编码，在相同的率失真下定将会获得主观效果更好的重构图像。依据HVS所具有的这种对频率系数敏感性的差异，提出一种对小波子带的加权方案，目的是使HVS敏感的子带系数被优先编码。

因为小波多尺度特性与 HVS初级视觉的空域频率多通道相吻合，因而可考虑通过空域频率揭示各子带的特性。文献[22]采用CSF(contrast sensitivity function)来描述HVS的频率敏感程度

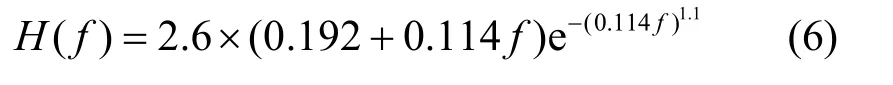
其中，f为空间频率，其单位为周期/度，取值范围为[0,32]，H(f)为HVS对f的敏感程度。首先对f进行采样并通过式(6)获得一系列CSF数值，对这些数值进行小波分解，并计算各子带的平均值，对这些平均值进行线性拉伸，使其最小值为1；其次，将所得到的1D子带的权重值通过图3的顺序进行2D子带映射，以此形成2D小波子带的视觉权重（如表 1所示，其中，小波变换为3级）。

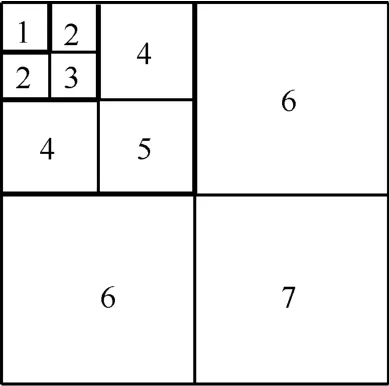
图3 子带权重顺序

表1所示权重来自于自然图像，考虑到时域低频帧系数的分布与自然图像相类似，本文算法仅对时域低频帧进行了如此加权处理，而对于时域高频帧不适合进行相应的加权处理。

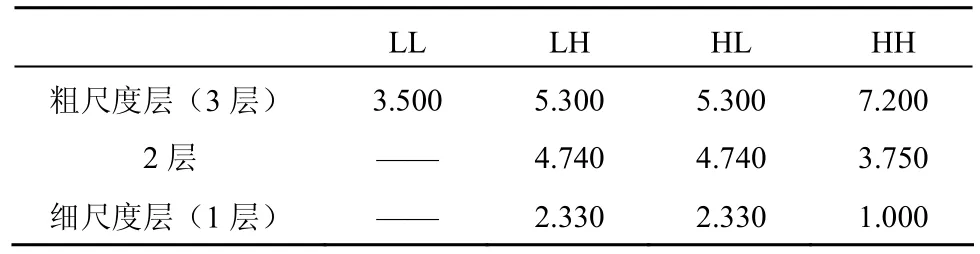
表1 3级9/7小波分解后得到的视觉权重

5 本文提出的视频可分级编码算法的实现

在混合时空方向树结构和基于 HVS加权处理的基础上，给出如下基于3D小波的视频可分级编码算法。

符号约定如下。

Ti为进行第i轮量化所采用的阈值，初值为 T0。

LIP、LSP分别为不重要系数表和重要系数表。

LIS为不重要像素的集合。

C为标志位，用于标识当前所处理的图像分量，其取值分别为Y、U和V。

O( x, y, z)表示节点(x, y, z)的直接子节点集合。

D( x, y, z)表示节点(x, y, z)的所有子系数集合。

L( x, y, z)表示节点(x, y, z)的除直接子节点外的所有子系数集合。

A、B型树分别指在编码 LIS的每个节点(x, y, z)时分别需要检查 D ( x, y, z)、L( x, y, z)是否有重要系数。

W和h分别为空间LL的宽、高度。

F为时域最低频帧的数量。

算法的主要过程如下。

Step1 对输入视频进行 GOP 划分（每 16帧为一个 GOP），并且对每个 GOP分别进行 Lt级MCTF和 Ls级小波变换（其中，Lt和 Ls实验中分别选为4和3）。

Step2 对3D小波子带按第4节的加权模型加权处理。

Step 3 进行初始化。

Step 3.1 对每个GOP的时空小波系数，计算其初始量化阈值 T0

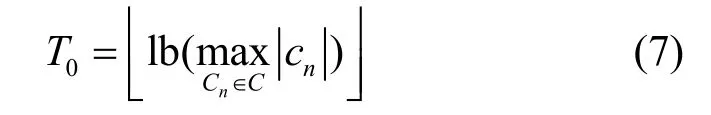
其中，C为加权处理的小波系数集合；

Step 3.2 赋 0i= ，LSP=φ；将时、空方向同时为最低频子带的所有系数(参见图 2中第一帧左上角的 a,b,c,d系数)放入LIP和LIS中，其中，Y分量系数在前(此时令C=Y)，U、V分量系数在后(此时分别令C=U和C=V)。同时记LIS中每个节点的类型为A型。

Step 4 重要系数搜索。

Step 4.1 根据分量类型，对 LIP中的节点(,,)x y z,将其对应的系数与相应的阈值iT比较，当系数的绝对值大于或等于iT时，输出“1”及符号位，同时将系数移至LSP表；否则输出“0”。

Step 4.2 按3.2节时空混合方向树搜索重要系数并对LIS进行调整。对于父节点(,,)x y z，其直接子节点可划分为下列4种情况。

Case 1 若(,,)x y z是时间域及空间域低频子带中的节点（如图2第一帧左上角的a, b, c, d所示），其直接子节点（下一层）又被划分为 2种情况。

1) 如果为左上角2×2块中的a系数, 其子节点集合为

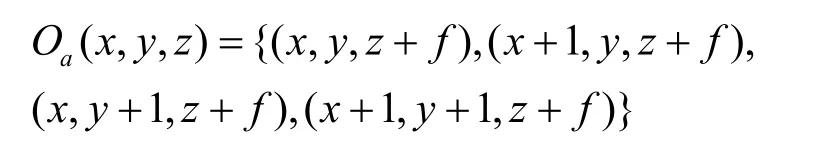
2) 若为22×小块中的b,c,d节点,此时子节点的集合为

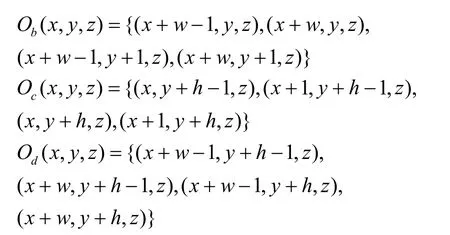
Case 2 若（x, y , z）为时域最高频的空间LL中的节点（参见图 2三、四帧左上角 a,b,c,d），其直接子节点集合:

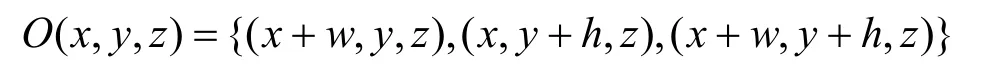
Case 3 若(x, y, z)是时间域其他空域低频子带中的节点（参见图2中第2帧的左上角a,b,c,d系数），此时其直接子节点集合为

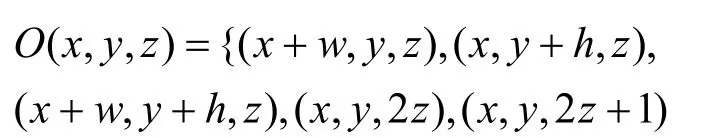
Case 4 若(,,)x y z为各帧中空域高频子带的节点（参见图2中第一帧右上角4个b，以及第二帧中右上角a, b, c, d系数），此时其直接的子节点集合为

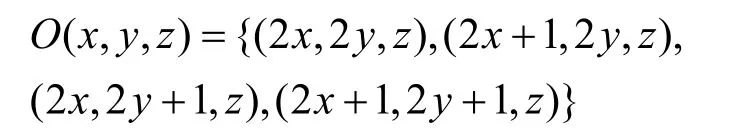
Step 4.3 针对当前分量C，对LIS表中对应每个节点(x, y, z)的重要性进行检测。如果当前树是A型，转至Step 4.3.1；否则转到Step 4.3.2。

Step 4.3.1 检测 D ( x, y, z)的重要性，如果重要，输出“1”，并通过阈值 Ti判断该节点的直接子节点的重要性，若重要，输出“1”及符号位，并将其移入LSP；如不重要则输出“0”，并将其移至LIP表。进一步，如果 L ( x, y, z)存在，将在LIS表的末端移入该节点，来作为B型树。若 D ( x, y, z)不重要，则输出“0”。

Step 4.3.2 检测 L ( x, y, z)的重要性，如果重要则输出“1”，同时把该节点的直接子节点移至 LIS表的末端作为A型树，并把父节点自LIS中删除；如果 L ( x, y, z)不重要，输出“0”。

Step 5 重要系数幅值细化。

Step 5.1 针对当前分量C，考察LSP表中对应的重要系数，如果它位于区间[Ti, 1.5Ti)则输出“0”，否则输出“1”。如果形成的码流达到了目标码率，则结束算法；否则转向Step 5.2。

Step 5.2 i = i + 1 ， Ti= Ti-1/2。如果 Ti= 0 ，结束算法；否则转向Step 4。

6 实验与分析

对CIF 30Hz格式的6个视频序列的1～96帧或1～128帧进行仿真实验，这6个视频序列分别为：Hall Monitor、Akiyo、Miss America、Mobile &Calendar、 Foreman和Mother & Daughter。实验在VidWav平台上进行，每个GOP为16帧，选用t+2D方式的3D小波变换，时间维进行了 Lt= 4 级5/3小波的 MCTF，空间采用了 Ls= 3 级的9/7提升小波的分解，对Y、U、V 3个分量进行顺序编码。实验结果与文献[15]的非对称树结构方案和文献[17]的时空方向树方案进行了比较，其中，文献[15]与本文算法的结果在VidWav平台上得到，文献[17]的结果源自原文。

6.1 主观解码质量

由于兼顾了 HVS视觉特性，有利于解得高主观质量的视频图像。所提出算法与非对称树编码方案在 128kbit/s和 512kbit/s码率下编、解码 Miss America和Mobile & Calendar序列，并进行了比较。图4为2序列第1帧的解码结果。从解码图像可看出，在128kbit/s码率下，所提出算法的“振铃效应”要弱于文献[15]算法；在512kbit/s码率下，所提出算法获得了较高的主观解码质量，而此时文献[15]算法解码帧中振铃效应仍较为明显（参见图5中数字边缘及上方的日历）。可见本文小波子带系数加权方案将会在一定程度上改善重构视频的主观质量。

6.2 解码客观质量

本文对 Mother & Daughter、Hall Monitor、Akiyo、Miss America和 Mobile & Calendar的 1～96帧在128kbit/s、256kbit/s和512kbit/s码率下解码的PSNR进行了统计（如表2所示），对于运动幅度低的 Miss America和运动幅度高且细节丰富的Mobile & Calendar，本文算法均获得了较高的PSNR。提出算法Y分量解码的平均PSNR高于文献[15]0.65dB，而U、V解码分量较文献[15]平均高1.75dB和1.77dB。

表3列出了Foreman和Miss America的1～128帧分别在500kbit/s、1 000kbit/s和1 500kbit/s下本文算法与文献[17]算法重构PSNR的统计结果，对于Y分量，所提出算法获得的平均PSNR较文献[17]高0.23dB，而解码 U、V分量的平均 PSNR分别高出文献[17]2.11dB和1.72dB。可见中低码率下本文算法的解码质量与[17]相比有一定改进，这源于所提出的混合时空方向树可以更加有效地对大幅值系数进行定位。

图4 本文算法与文献[15]中非对称树结构算法解码的主观质量比较

图5 本文算法与文献[15]中非对称树结构算法解码的细节主观质量比较

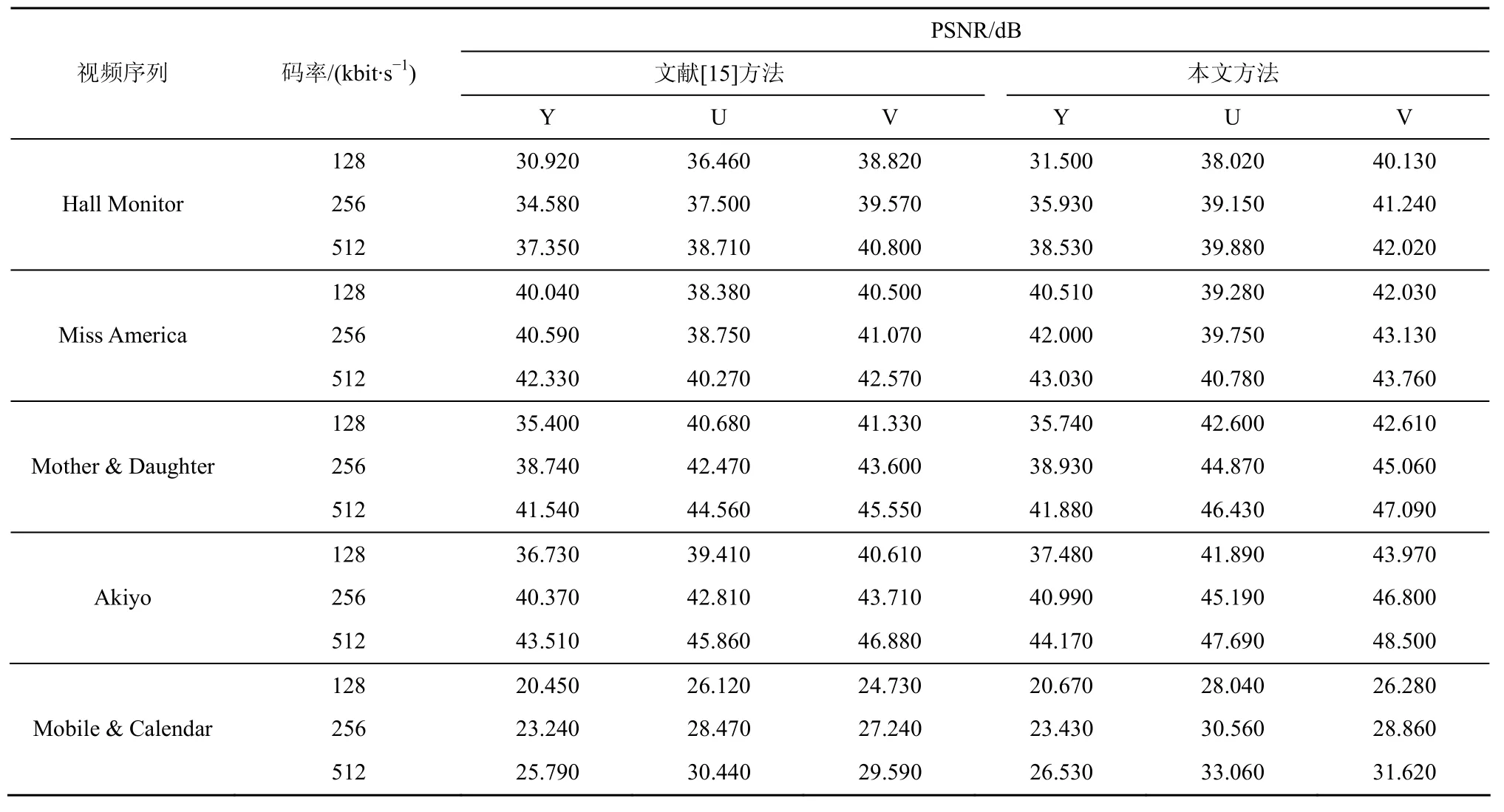
表2 不同码率下所提出算法与非对称树结构算法的重构结果比较

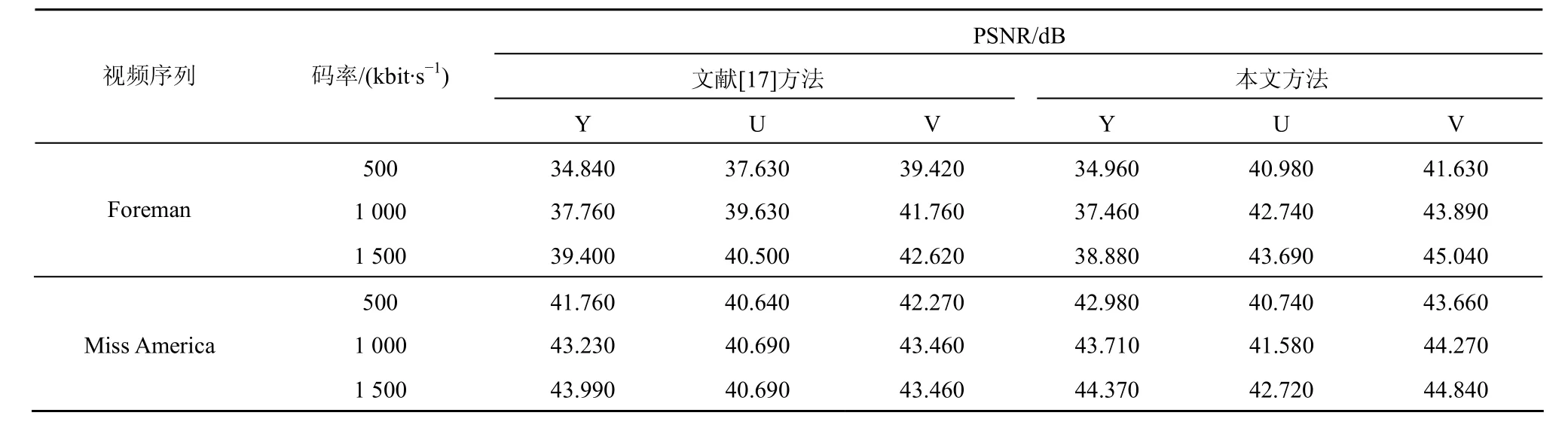
表3 不同码率下所提出算法与时空方向树结构算法的重构结果比较

表4 本文算法与基于非对称树结构算法以GOP(16帧)为单位的平均编、解码时间比较

6.3 编、解码时间比较

表4给出了本文算法与基于非对称树结构算法以GOP(16帧)为单位，前96帧视频序列的平均编码解码时间比较，从表中可以看出，本文算法在编码方面所用时间要低于基于非对称树结构算法，解码时间与对比文献相差不大，而且从文献[17]可知，基于非对称树结构算法与基于时空方向树的编码算法在时间复杂度方面近似，因此本文算法的时间复杂度要低于基于非对称树结构与基于时空方向树结构的2种对比算法。分析原因主要在于本文算法提出的混合时空方向树结构更有利于定位重要系数，从而减少扫描次数，降低了编码时间。

7 结束语

本文在分析3D小波变换时域低、高频帧系数分布特点的基础上，提出一种混合时空方向树结构，并依据 HVS特性提出一种基于小波系数敏感函数的子带加权模型，进一步提出了一种视频可分级编码算法。所提出的算法的优点体现在：1）根据低、高频系数自相关特性，采用了相应的树形结构，减少了用于重要系数定位的同步信息；2）根据 HVS对不同频率分量的敏感差异，对小波系数进行了加权改造，提高了解码的主观视觉质量。

[1] SCHWARZ H, MARPE D, WIEGAND T. Overview of the scalable video coding extension of the H.264/AVC standard[J]. IEEE Trans on Circuits and Syst for Video Technol, 2007, 17(9):1103-1120.

[2] 王相海.视频细粒度可分级编码研究进展[J].计算机科学, 2006,33(7):75-80.WANG X H. Research progress on fine granularity scalability video coding[J]. Computer Science, 2006, 33(7):75-80.

[3] 王相海,宋传鸣. 图像及视频可分级编码[M]. 北京:科学出版社,2009.WANG X H, SONG C M. Image and Video Scalable Coding[M]. Beijing: Science Press, 2009.

[4] DAS A, HAZRA A, BANERJEE S. An efficient architecture for 3-D discrete wavelet transform[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2010, 20(2):286-296.

[5] KIM B, XIONG Z, PEARLMAN W A. Low bit rate, scalable video coding with 3-D set partitioning in hierarchical trees (3-D SPIHT)[J]. IEEE Trans on Circuits and Syst for Video Technol, 2000, 10(12): 1374-1387.

[6] 丁文奇, 胡佳, 张立明.充分减小树间冗余的优化三维 VSPIHT视频编码方法[J].计算机辅助设计与图形学学报, 2005, 17(3):563-569.DING W Q, HU J, ZHANG L M.Optimal 3D-SPIHT video coding method by reducing redundancy between tress[J]. Journal of Computer-Aided Design & Computer Graphics, 2005, 17(3):563-569.

[7] CHENG C C, PENG G J, HWANG W L. Subband weighting with pixel connectivity for 3-D wavelet coding[J]. IEEE Trans on Image Process, 2009, 18(1):52-62.

[8] WANG H M, PAN X Z. Video compression coding based on the improved 3D-SPIHT[A]. 2010 International Conference on Computer Application and System Modeling (ICCASM)[C]. Taiyuan, China 2010.108-111.

[9] ISO/IEC JTC 1/SC 29/WG 11. Wavelet Video Coding – an Overview:w7824[R]. MPEG 2006.

[10] ISO/IEC JTC 1/SC 29/WG 11. Status Report on Wavelet Video Coding Exploration: N7822[R]. MPEG 2006.

[11] 宋传鸣. 基于多尺度分析的视频可分级编码技术研究[D]. 南京:南京大学, 2010.SONG C M. Research on Scalable Video Coding Based on Multiscale Analysis[D]. Nanjing:Nanjing University, 2010.

[12] SHAPIRO J. Embedded image coding using zerotree of wavelet coefficients[J]. IEEE Trans on Signal Process, 1993, 41(12):3445-3462.

[13] SAID A, PEARLMAN W A. A new, fast, and efficient image codec based on set partitioning in hierarchical trees[J]. IEEE Trans on Circuits and Syst for Video Technol, 1996, 6(3):243-250.

[14] 张宗平, 刘贵忠, 侯兴松.一种改进的三维小波视频编码[J]. 西安交通大学学报, 2001, 35(6):595-599.ZHANG Z P, LIU G Z, HOU X S. Improved 3D-wavelet video coder[J]. Journal of Xi’an Jiaotong University, 2001, 35(6):595-599.

[15] HE C, DONG, ZHENG, GAO Z. Optimal 3-D coefficient tree structure for 3-D wavelet video coding[J]. IEEE Trans on Circuits Syst and Video Technol, 2003, 13(10):61-972.

[16] KHAN E, GHANBARI M. Very low bit rate video coding using virtual SPIHT[J]. IEE Electronic Letters, 2001, 37(1):40-41.

[17] ZHANG L, WANG D, VINCENT A. Decoupled 3-D zerotree structure for wavelet-based video coding[J]. IEEE Trans on Broadcasting, 2008,54(3):430-436.

[18] KASSIM A A, TAN E H, LEE W S. 3D color set partitioning in hierarchical trees[J]. Circuits Syst Signal Process, 2009, 28:41-53.

[19] MOINUDDIN A A, KHAN E, GHANBARI M. The impact of tree structures on the performance of zerotree-based wavelet video codecs[J]. Signal Processing:Image Communication, 2010,25(3):179- 195.

[20] 姚庆栋, 毕厚杰, 王兆华等. 图像编码基础[M]. 北京:清华大学出版社, 2006.YAO Q D, BI H J, WANG Z H, et al. Fundamentals of Image Coding[M]. Beijing: Tsinghua University Press, 2006.

[21] 李玲, 王向阳.基于视觉敏感特性的小波域图像编码算法研究[J].小型微型计算机系统, 2010, 31(4):780-783.LI L, WANG X Y. New image coding algorithm contrast sensitivity[J].Mini-MicroSystems, 2010, 31(4):780-783.

[22] BEEGANA P. Wavelet-based image compression using human visual system models[A]. Electrical Engineering Department of Virginia Polytechnic Institute[C]. Virginia, USA, 2001.