认知无线电中认知用户的重新建模与性能分析

林威，付宇，张钦宇，王野，王胜

（哈尔滨工业大学 深圳研究生院 通信工程研究中心，广东 深圳 518055）

1 引言

无线通信业务需求的快速增长，使频谱资源日益紧缺。目前采用的静态频谱分配政策常常导致某些时段和地区频谱使用频繁，而其他时段和地区频谱空闲。由于“独占”的授权工作方式不允许非授权用户使用空闲频段，频谱资源无法得到充分利用，造成了大量的资源浪费。根据美国联邦通信委员会(FCC)统计，现有已分配频谱的利用率在15%～85%之间[1]。为了公平、有效地使用频谱资源，FCC提出一种新型的频谱共享技术——认知无线电 (CR, cognitive radio)[2,3]。

CR技术能有效地解决频谱利用率低、频谱资源紧张的状况，并以灵活、低价等特点受到广泛关注。在感知共享的应用环境下，授权系统开放未被授权用户(PU, primary user)使用的频谱资源，支持认知用户(SU, secondary user)通信。PU是网络的合法用户，具有高优先级，随机接入未被其他PU占用的频谱；SU不具备频谱授予权，以不影响PU的正常通信为前提，利用频谱空穴检测技术[4]获取PU信息后接入空闲频谱。为了避免对PU产生干扰[5]，SU在PU再次出现时退避。

将PU和SU的行为映射为Markov模型[6]是分析认知网络(CRN, cognitive radio network）性能的有效方法。文献[7]提出的PU优先的Markov模型，能够使CR系统有效、公平地利用未被PU使用的频谱，但是该方案只针对单信道场景进行了分析，对多信道系统的参数设置和建模则比较复杂，没有给出解决方案。文献[8]使用基于 CR-OFDM 的Markov模型来讨论SU如何接入授权频段的问题，并在此基础上，提出一种基于退让机制的动态频谱接入方案，通过伺机利用频谱空穴来提高频谱利用率，但在PU出现时，SU没有机制切换到其他空闲频段继续通信，因此频谱利用率仍有进一步提升的空间。文献[9]和文献[10]均使用三维连续时间Markov链3D-CTMC模型来模拟CRN接入策略，清晰地刻画了PU和SU的行为，分析了基本频谱接入策略下认知系统的性能。文献[9]证明掉话率是限制CR系统吞吐量的主要因素，并提出信道预留频谱接入策略，该策略通过牺牲阻塞率换取掉话率，最大化系统吞吐量。而文献[10]通过引入频谱切换技术，使SU在信道被抢占后可再次接入空闲信道，降低了掉话率，保证了服务的完整性，并证明在掉话率和信道利用率方面频谱切换技术优于基本频谱接入策略和信道预留频谱接入策略。

但是，在文献[9]的基本频谱接入策略和文献[10]的频谱切换接入策略所使用的3D-CTMC模型中，掉话状态和阻塞状态均为瞬态，不存在稳态概率，导致衡量认知系统QoS的主要指标（阻塞率和掉话率）的定义不准确，无法求得系统性能参数。此外，文献[9]的信道预留频谱接入模型将系统中的PU总数目错误计为预留区域中PU数目，造成PU错误地使用非预留信道，产生不必要的掉话。

针对上述问题，为真实地刻画CRN接入过程，准确地模拟PU和SU的行为，本文对CRN接入部分PU和SU的行为重新进行了建模，并给出了阻塞率、掉话率的计算式。利用矩阵几何理论和离散事件仿真的事件调度法，求得该模型下各状态的稳态概率和衡量系统QoS的主要指标，验证了本文所提模型的可靠性。在此基础上，以最大认知系统吞吐量为目标，求解最优的预留信道数来设计信道预留频谱接入策略。对3种频谱接入策略进行了性能评估，针对不同的业务类型选取最佳的接入策略。

2 模型分析与重建

本节对第1节提到的3种接入策略进行深入地讨论，论证现存数学模型中存在的问题。针对此问题重新建模，给出阻塞率和掉话率的计算式。

2.1 基本频谱接入策略

采用PU占优的认知系统和授权系统共享频谱资源方式，对相同频带采用时分复用方式接入，每一频带同一时刻只容纳一个用户。系统中共有N个等带宽独立频带，假设PU和SU的到达速率分别为λp和λs，服从泊松过程，服务时间分别服从均值为的负指数分布。图1描述了基本频谱接入过程。在 t0时刻，SU利用空穴检测技术占用空闲频带F2和 F5；在t1时刻，系统无空闲频带，处于阻塞状态，拒绝SU接入；在t2时刻，PU随机选择频带接入，强制中断F2上通信的SU，SU退出系统，此时系统处于掉话状态；经过可忽略的延迟时间 △t，系统处于图1(d)所示稳定状态。

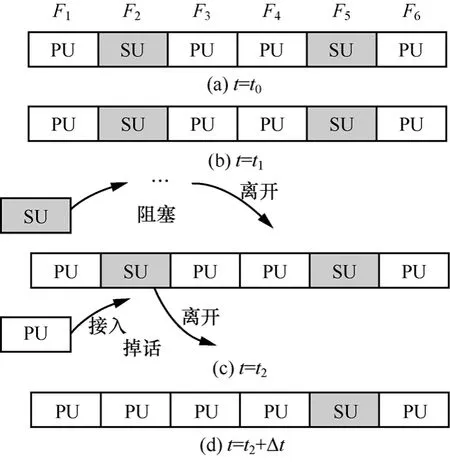
图1 基本CRN频谱接入

在文献[9]中采用的3D-CTMC模型中，状态表示为(i,j,k)，其中，i，j分别代表系统中PU和SU的数目；k表示系统发生的事件，k=0表示 PU和SU间无碰撞，k=1为发生掉话，k=2为系统阻塞；P( i , j, k)表示系统处于状态( i , j, k)的稳态概率。阻塞率和掉话率分别定义为所有阻塞状态和掉话状态的概率和，即文献[9]中式(9)、式(10)：

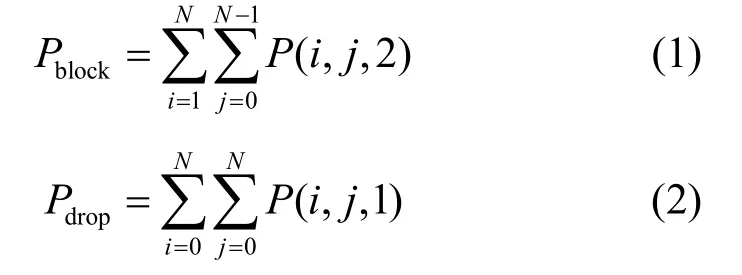
当系统中有1个SU时，如果新的PU抢占了SU信道，系统状态由(0,1,0)转移到状态(1,0,1)后以概率 1（速率∞）稳定在状态(1,0,0)，由此可知状态(1,0,1)为瞬态，存在时间极短，可忽略不计。在SU试图接入满载系统的过程中同样存在瞬态，例如：当系统处于状态(2,N - 2 ,0)时，拒绝新的 SU接入，转移到状态(2,N - 2 ,2)后以∞速率回到状态(2,N - 2 ,0)，其中，状态(2,N - 2 ,2)是瞬态。从上述状态转移过程来看，所有的掉话和阻塞状态（ k = 1 ,2）均是瞬态。由于瞬态不存在稳态概率，式(1)、式(2)作为 P ( i, j, 2 )和 P ( i, j, 1 )的函数没有理论解，因此阻塞率和掉话率的定义是不准确的。

针对上述 3D-CTMC模型存在的问题，采用2D-CTMC模型对PU和SU的行为重新建模，如图2所示，状态空间表示为

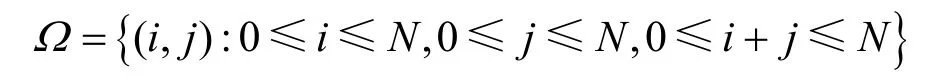
其中，i, j分别代表系统中PU和SU的数目，πi,j表示系统处于状态(i, j)的稳态概率。

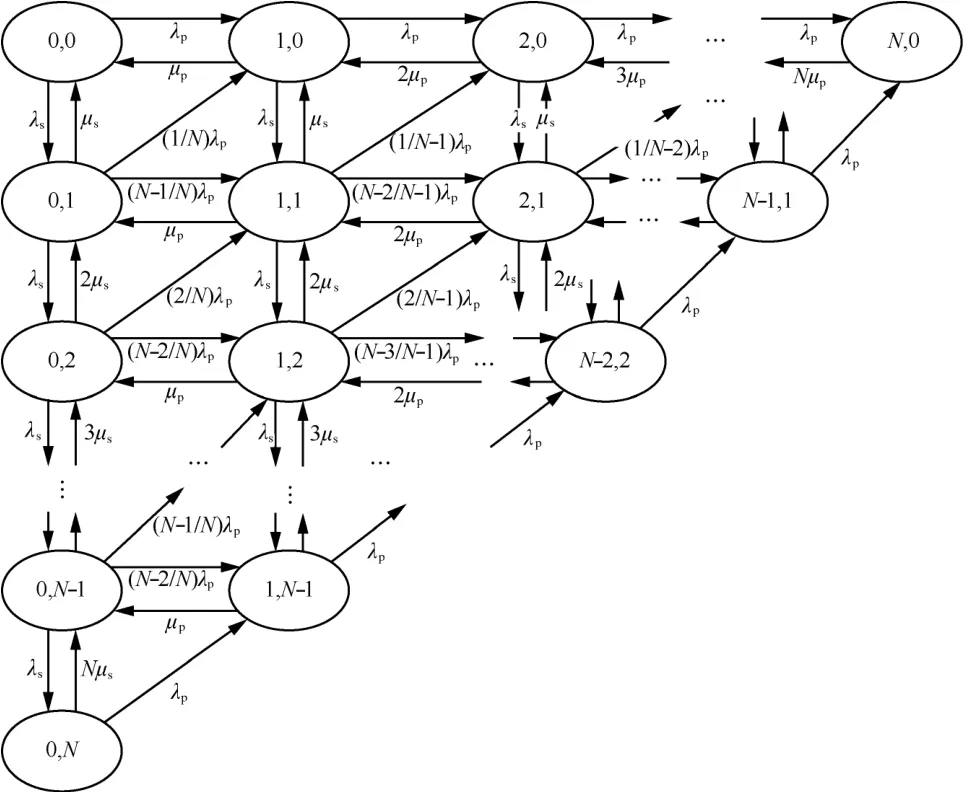
图2 修正后的2D-CTMC基本频谱接入模型

当i + j ≤ N , j ≥ 1时，若新的 PU接入空闲信道，系统状态(i,j) 将以转移率转移到状态(i+1,j) ；若新的PU抢占了SU信道，SU掉话，系统状态(i,j)将以转移率转移到状态(i + 1 , j - 1 )。当i+ j= N 时，新的PU抢占了SU的信道，系统处于阻塞状态，拒绝新的SU接入，系统状态不变。

这里重新给出阻塞率和掉话率的定义，并对文献[9]中的式(9)、式(10)进行修正。

阻塞率：单位时间内无法接入系统的SU数量与试图接入系统的SU数量之比。

掉话率：单位时间内通信被迫中断的SU数量与成功接入系统的SU总数量之比。

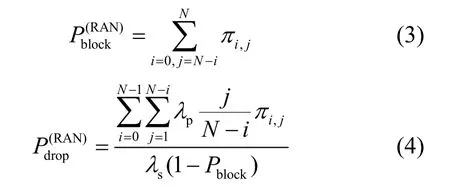
2.2 频谱切换接入策略

对于实时性要求较高的业务，通信被迫中断通常比阻塞更加难以接受。为保证服务的完整性，提高已接入系统的SU的服务质量，在基本频谱接入策略的基础上引入了频谱切换的概念[11,12]，使得SU在为PU让出频谱后可以寻找其他空闲频谱继续通信。

文献[10]采用的 3D-CTMC模型中，状态表示为(i,j,k)，其中，i，j分别代表系统中PU和SU的数目；k表示系统发生的事件，其中，k=0为PU和SU间无碰撞，k=1为频谱切换，k=2为掉话，k=3为系统阻塞；P(i,j,k)表示系统处于状态(i,j,k)的稳态概率。同理于2.1节对系统状态的分析，该模型中掉话状态、阻塞状态、延迟状态均为瞬态，不存在稳态概率。此外，由于频谱切换带来的延迟对系统性能的影响很小，（见附录），通过使用最优的频谱切换算法和有效的频谱切换技术可进一步优化延迟时间，因此，本文不考虑频谱切换带来的延迟，将延迟状态视为不存在。

下面采用2D-CTMC对频谱切换接入策略重新建模，如图3所示，状态空间表示为

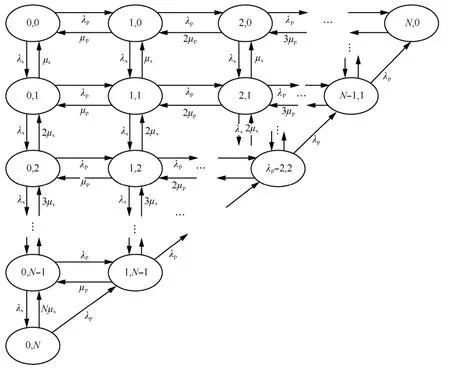
图3 修正后的2D-CTMC带切换频谱接入模型

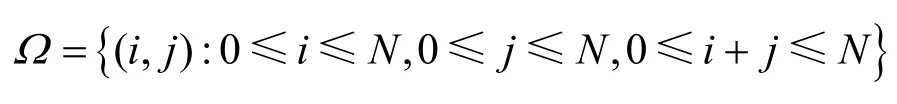
其中，i, j分别代表系统中PU和SU的数目。下文用πi,j表示系统处于状态(i, j)的稳态概率。

当i+ j≤ N - 1, j ≥1时，新的PU抢占了SU的信道或者接入空闲信道，系统状态将(i, j)以转移率λp转移到状态(i+1,j)。当i+j=N时，系统处于阻塞状态，拒绝新的SU接入，系统状态保持不变。当 i + j = N , j ≥ 1时，系统无法为被抢占信道的SU提供信道，SU掉话，系统状态(i, j)以转移率λp转移到状态(i + 1 , j - 1 )。

阻塞率的计算式与基本频谱接入策略的相同，由于掉话只发生在系统中无空闲信道时，因此掉话率不同。

此外，考查衡量频谱切换策略中另一个重要因素——频谱切换概率，指SU频谱切换次数与通信次数的比值。

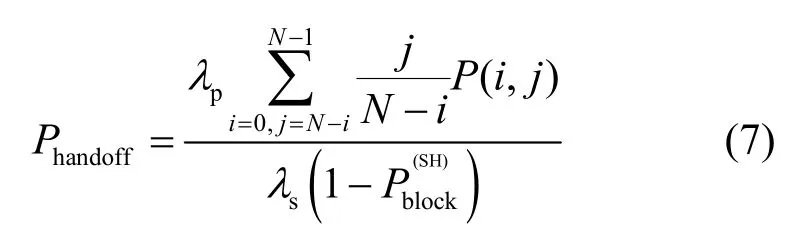
2.3 信道预留接入策略

在信道预留接入策略中，信道按位置被划分为预留区域和非预留区域2部分。授权基站安排PU优先接入预留区域的空闲信道，在PU和SU接满非预留区域的信道后，周期性地发送通告阻止 SU接入预留区域。

文献[9]采用的 3D-CTMC模型对预留信道[13,14]数为 R的 N信道系统进行建模。系统状态表示为(,,)i j k，其中，i，j分别代表系统中PU和 SU的数目；k表示系统发生的事件，其中，k=0为PU与SU间无碰撞，k=1为掉话，k=2为系统阻塞； (,,)P i j k表示系统处于状态(,,)i j k的稳态概率。

当iR≥时，若新的PU抢占SU的信道，SU掉话，系统状态(,,0)i j 以转移率转移到状态(i + 1 , j - 1 ,1)；若新的PU接入空闲信道，系统状态(,,0)i j 以转移率转移到状态但实际情况并非如此，在系统PU数目较多时，由于预留区域的PU完成服务后离开系统，非预留区域有PU存在，那么系统PU数目不少于R，预留区域仍可能有空闲信道，新的PU将接入预留区域，SU不掉话，此时系统状态将直接以转移率λp进入状态(i + 1 ,j,0)。由此可知系统中部分状态转移不正确，产生此错误的根本原因在于此模型将预留区域和非预留区域的PU一起计数，把PU总数错误地理解为预留区域中PU数，造成PU没有接入预留信道，产生不必要的掉话。此外，系统中部分状态仍为瞬态。

为了清晰地刻画预留区域和非预留区域中用户的行为，避免发生不必要的掉话，本文将2个区域中的PU分开计数。如图4所示，系统共有N个信道，为PU预留R个信道，系统状态空间表示为

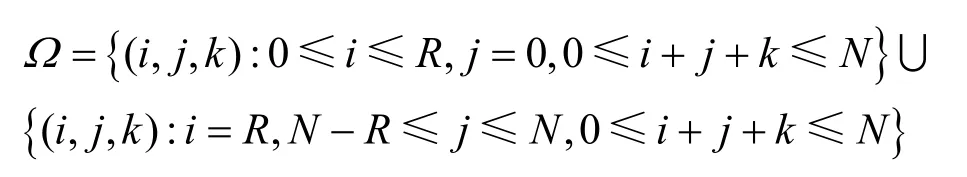
其中，i，j分别代表预留区域和非预留区域中 PU的数目，k代表非预留区域中SU的数目。下文用πi,i,k表示系统处于状态(i, j, k)的稳态概率。

当 i ≤R-1时，新的PU接入预留信道，不影响非预留区域的SU，系统状态(i, j, k)以转移率λp转移到状态(i + 1 ,j, k)。当 i = R, 1 ≤ j ≤ N -R 时，若新的PU使用非预留区域的空闲信道，则系统状态(,,)i j k以转移率转移到状态(i, j + 1 ,k)；若新的PU接入SU信道，SU掉话，系统状态(i, j, k)以转移率转移到状态(i, j + 1 ,k - 1 )；当 i = R , j+ k = N - R 时，系统阻塞，拒绝SU接入，系统状态不变。

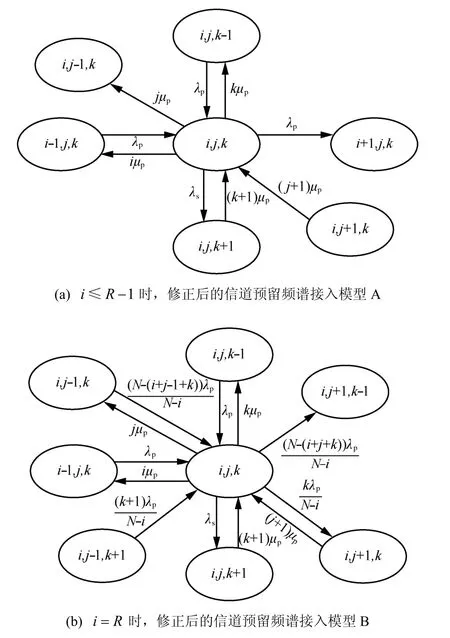
图4 修正后的信道预留频谱接入模型

根据图4得到阻塞率和掉话率的计算式为

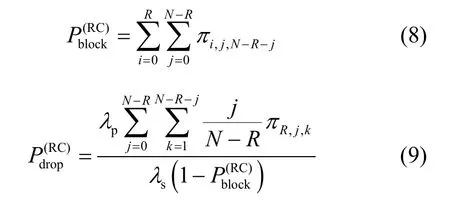
认知系统吞吐量作为系统性能的另一个重要指标，定义为单位时间内完成服务的SU数量。

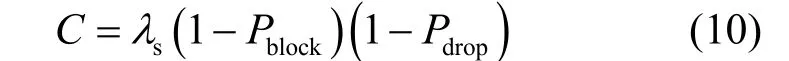
其中， λs( 1 - Pblock)为单位时间内成功接入系统的SU数量。

3 理论分析与离散事件仿真求解

本节以基本频谱接入策略为例，利用2.1节的数学模型进行理论分析和仿真实验，给出系统各状态的稳态概率、阻塞率、掉话率的求解方法。

3.1 矩阵几何法

矩阵几何法[15]作为研究随机模型的重要方法，可以求解多维Markov的稳态概率。

本文提出的数学模型表示的状态空间是一个拟生灭过程[16]。拟生灭过程是经典生灭过程从一维状态空间到多维状态空间的推广，其生成元矩阵为

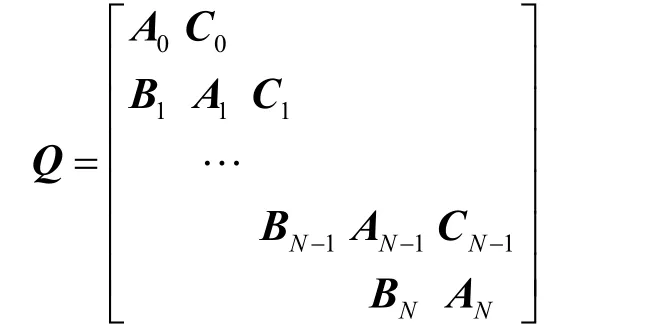
根据矩阵几何法，有如下关系式

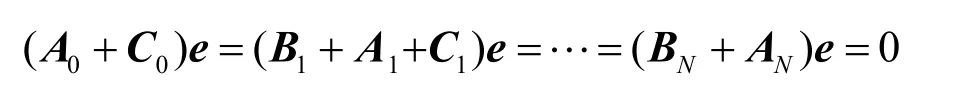
A具有负的对角线元素和非负的非对角线元素，其他矩阵是非负矩阵，e为元素全为1的列向量[15,17]。

为了适应分块的形式，将稳态概率写成一个1M×的向量（M为系统状态数）。

根据2.1节建立的基本频谱接入的状态转移图得到分块矩阵kA，kB和kC。

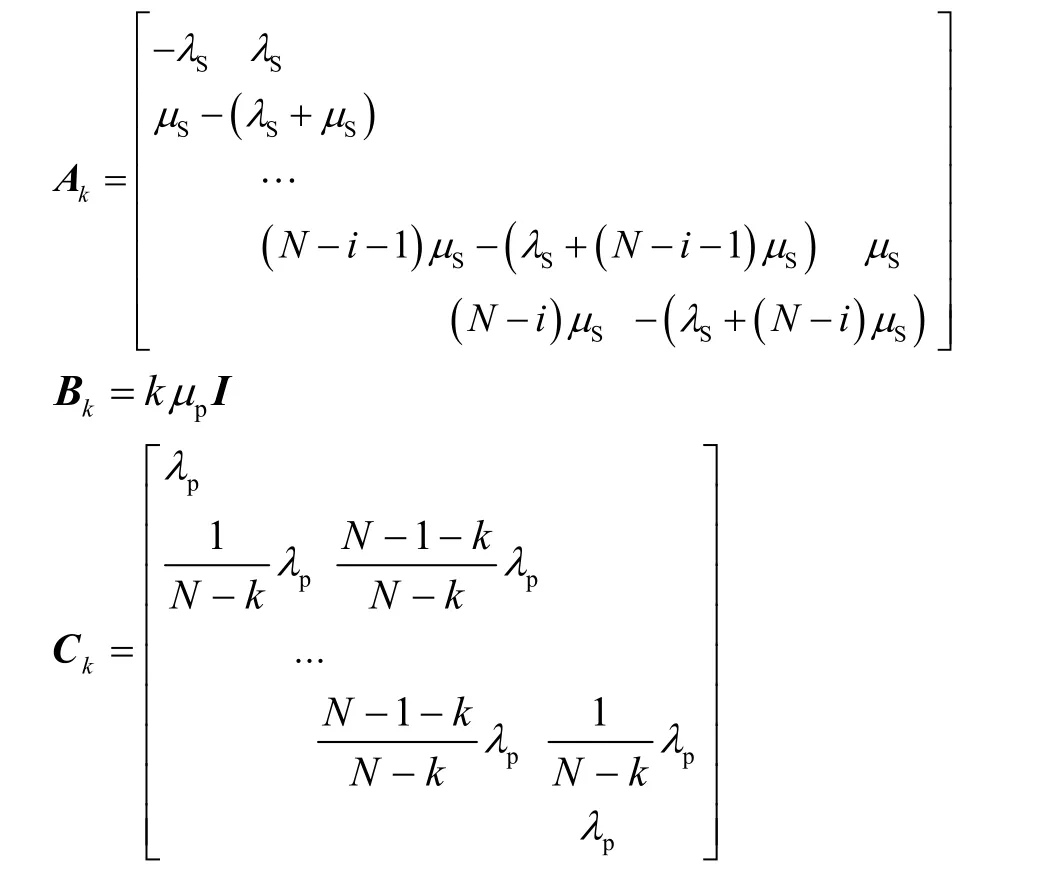
根据Netus理论[15]，由QBD过程稳态的边界条件πQ=0和正规化条件πe=1解得各状态的稳态概率 π0, π1, π2,… ,πN。将转移率矩阵Q的第一列替换为e，记作1Q。由于1=πe，可得到下列方程。

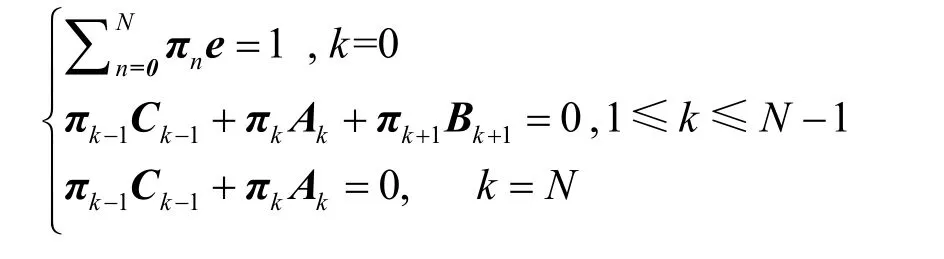
因此，有 π Q1= [ 1 , 0, … , 0,0]，对等式两边分别进行求逆运算，可得到系统的稳态概率为π=[1 , 0,0,… ,0] Q1-1。将π 代入式(2)和式(3)，求得阻塞率和掉话率。

这种方法简单易懂，但是只适用于Markov状态数较小的情况。当Markov状态数较多时，计算量极大，矩阵求逆极其耗费系统资源，稳态方程求解困难，甚至无法求解，因此采用计算机仿真法求解是有效的解决途径。

3.2 事件调度法

事件调度法[18]将事件例程作为基本仿真单元，按事件发生的先后顺序执行相应的事件例程。CRN接入过程分为接入系统、接受服务、退出系统3个事件，它们只在离散时间点发生变化，其变化域和空间状态具有离散性，因此采用离散系统仿真的事件调度法对该接入过程进行仿真，能够更真实地模拟系统中PU和SU的行为，具体步骤如下。

1) 设置仿真参数。包括仿真时间T、系统信道数目N、到达速率λP和λS、服务时间均值和

2) 初始化。生成用户的到达时间、服务时间、服务完成时间（到达时间间隔服从均值λP和λS的负指数分布，服务时间服从均值的负指数分布）放在事件发生时刻表中，将计数器归0。

3) 在规定的仿真时间内，进行时间扫描确定下一事件发生的时间，按时间顺序执行每个事件，更新相应的数据。

4) 在仿真时间到达时，统计数据（SU的总数量、阻塞数量、掉话数量），计算阻塞率和掉话率。

3.3 2种方法的结果评估

本节以基本频谱接入策略为例，采用以上2种方法求得阻塞率和掉话率，并分析与比较实验结果。为便于分析，将采用几何矩阵法和事件调度法得到的结果分别简写为理论解和仿真解。

由于部分用户（如话音业务）的服务时间由自身业务性质决定，不会发生变化，因此到达速率成为影响系统性能的重要因素。假设仿真时间 T=90 000s，λp=0～0.5个数/s，λs=0.4个数/s，的服务时间略低于PU的服务时间），在不同N值下分析阻塞率、掉话率随λp的变化规律。

在图5和图6中，随着λp的增大，更多的PU接入空闲信道和抢占SU信道，导致SU阻塞和掉话的数量增多，因此阻塞率和掉话率随λp呈上升趋势。在系统中的信道数较多时，用户可享用更多的资源，SU阻塞和掉话的数量会相应减少，阻塞率和掉话率较低。不同N值下，阻塞率和掉话率随λp的变化规律与理论分析结果相吻合，证实了利用的2D-CTMC模型的理论分析和实验仿真方法都是可靠的。

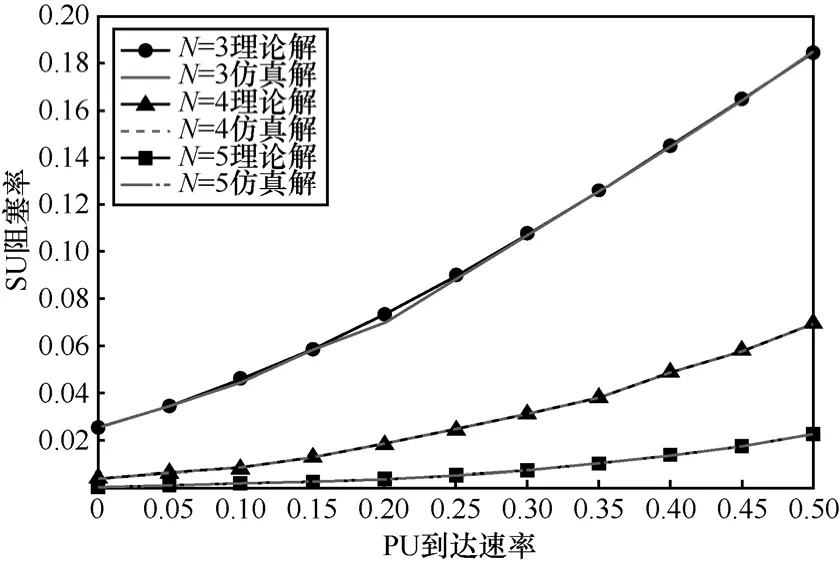
图5 以λp为变量的阻塞率

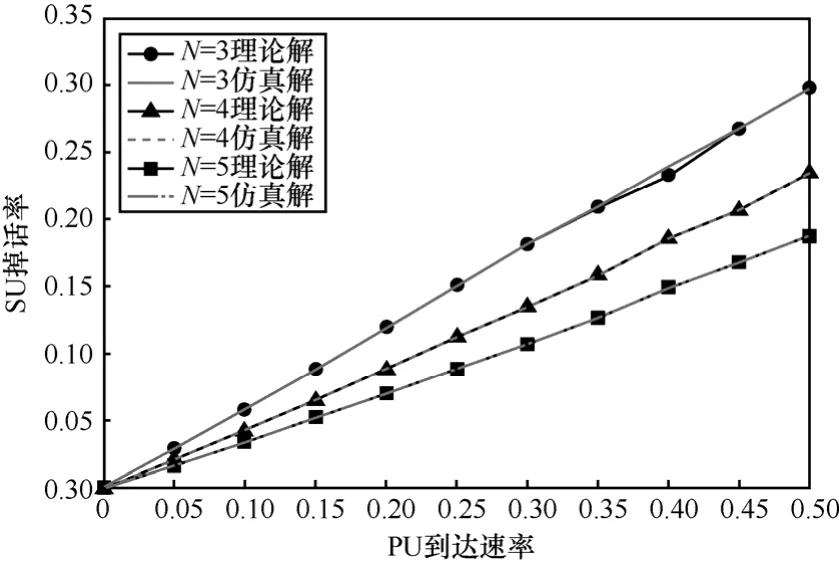
图6 以λp为变量的掉话率

4 3种接入策略实验分析

本节通过对第2节提出的3种CRN接入策略进行实验，得到阻塞率、掉话率、信道利用率的变化情况以及不同策略间的比较。在此基础上，以最大认知系统吞吐量为目标，运用拉格朗日松弛法找到最优预留信道数来设计最优的信道预留接入策略。最后，针对不同的业务类型，选择最佳的接入策略。

4.1 3种接入策略的性能分析

在本节，主要考虑2种参数情况下的阻塞率、掉话率、信道利用率：①p0～0.5=λ个数/s，s0.4=λ个数/s，

1）阻塞率

结合式(3)、式(5)和式(8)，得出上述参数情况下的阻塞率。如图7所示，3种接入策略的阻塞率均随 λp增大而增大。随着 λp增大，单位时间内 PU的到达频率加快、数量增多，PU占用了更多信道，相对SU的可用信道减少。如图8所示，3种接入策略的阻塞率均随 μp增大而减小，这是由于 μp的增大使得 PU的服务时间缩短，PU能在较短的时间内完成服务，信道处于空闲状态。

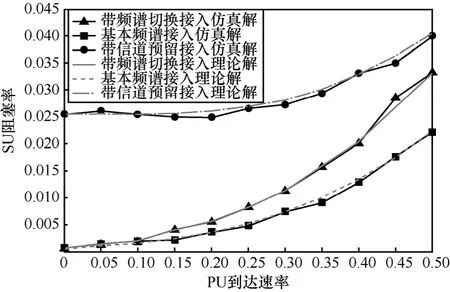
图7 以λp为变量的阻塞率

图8 以μp为变量的阻塞率

从图7和图8可以看出，在相同参数下，频谱切换接入策略阻塞率最大，信道预留接入策略次之。原因在于频谱切换技术允许被抢占了信道的SU可再次接入空闲信道，使得系统中空闲信道数量减少；信道预留策略将一部分信道分配给PU独享，只允许SU和PU共享非预留区域的空闲信道，SU的可用信道数量减少。

2) 掉话率

结合式(4)、式(6)和式(9)，得出上述参数情况下的掉话率。如图9所示，3种CRN接入策略的掉话率均随λp增大而增大。随着λp增大，更多的PU抢占了SU信道，导致被迫中断服务的SU数量增多。如图10所示，3种CRN接入策略的掉话率均随μp增大而减小。随着μp增大，PU的服务时间缩短使得系统中的空闲信道增多，SU在被PU抢占信道后可继续接受服务。

从图9和图10可以看出，在相同参数下，频谱切换和信道预留的接入策略均降低了掉话率，其中，频谱切换接入策略的掉话率最小。由于频谱切换接入策略下的SU在被迫让出信道后，可接入其他空闲信道，这使得掉话数减少。信道预留接入策略中PU优先接入预留信道，减少了占用非预留区域中SU信道，掉话数随之减少。

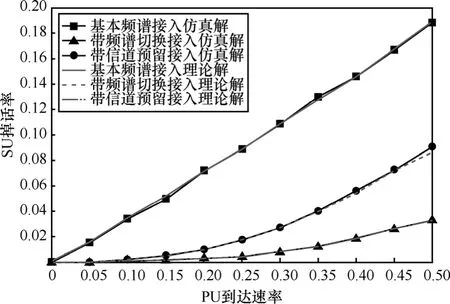
图9 以λp为变量的掉话率

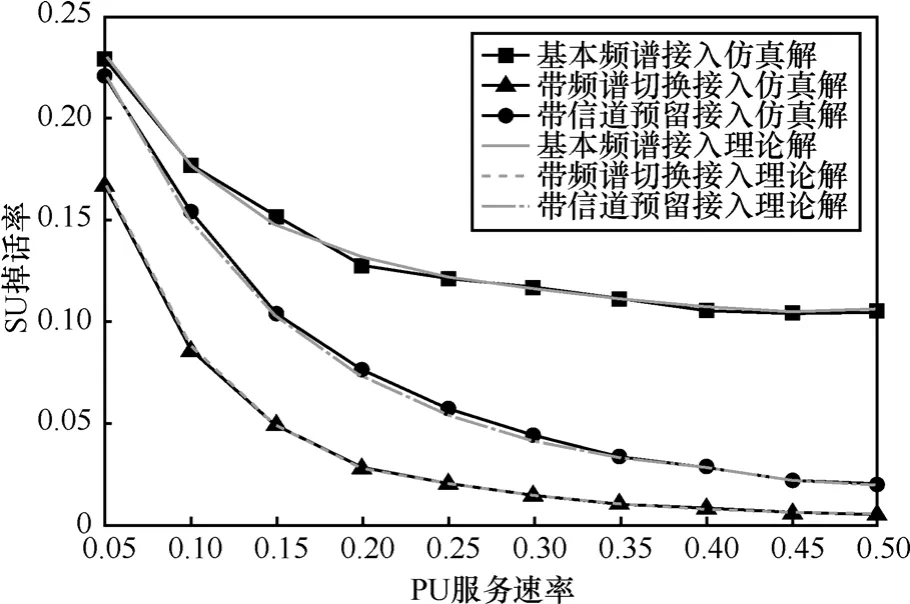
图10 以μp为变量的掉话率

3) 信道利用率

CR的提出旨在解决部分地区和时段频谱资源利用率低的问题，因此信道利用率成为衡量 CRN性能的重要指标。

信道利用率指信道平均被占用的程度，即系统中正在通信的用户数量与信道数目之比。根据定义给出3种策略下信道利用率的数学表达式。

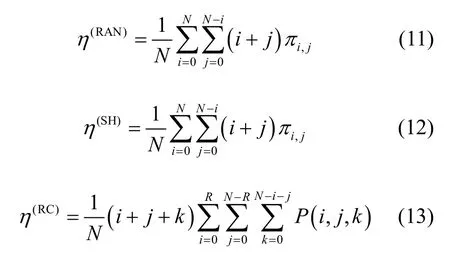
下面以λp为变量进行实验，考查3种接入策略下信道利用率的变化情况（参数设置与图7一致）。

结合式(11)、式(12)和式(13)得出上述参数下的信道利用率。如图 11所示，随着 λp增大，系统中更多信道被使用，那么3种接入策略的信道利用率均增大。从图11中可以看出，引入频谱切换后，SU在被迫让出信道后能再次接入空闲信道，信道利用率为基本频谱接入策略的2倍。信道预留接入策略由于只允许SU接入非预留区域，预留区域的信道没有得到充分利用，信道利用率与基本频谱接入策略近似。

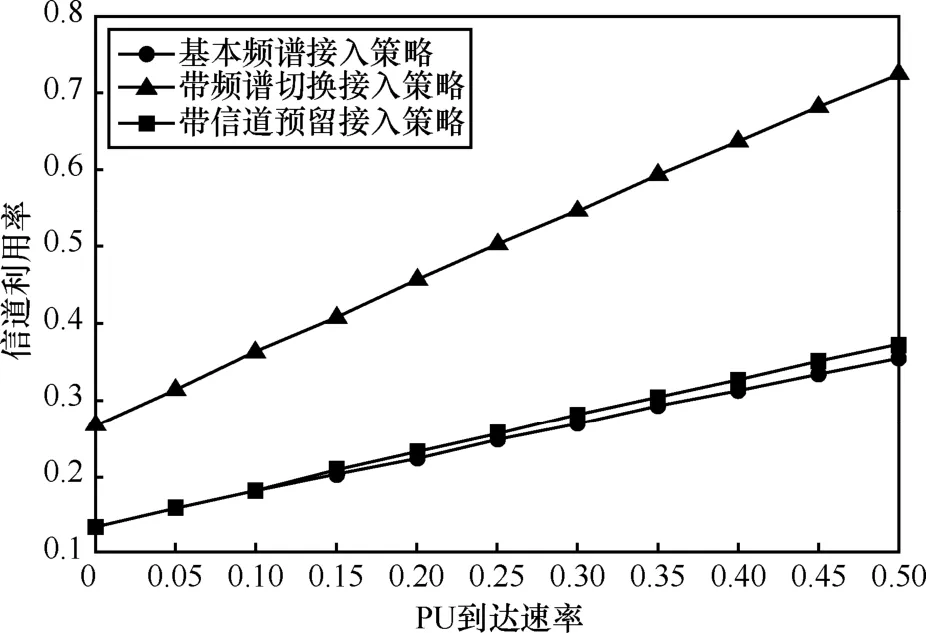
图11 以λp为变量的信道利用率

4.2 信道预留接入策略的优化

基于4.1节的分析，了解到信道预留接入策略以牺牲阻塞率来换取掉话率，不同的预留信道数将会带来不同的阻塞率和掉话率。那么，选取适当的预留信道数目成为设计该策略的关键问题。

首先，以预留信道数目为变量进行实验，考查阻塞率和掉话率的变化情况。参数设置如下：λp=0.3个数/s，λs=0.4个数/s，实验结果如图12所示，随着预留信道数的增多，SU可使用的信道数减少，导致SU无法接入系统，阻塞率逐渐增大；同时，PU独享的信道数目增多使得更多的PU可以接入预留信道，无需抢占非预留区域的SU信道，掉话率逐渐减小。

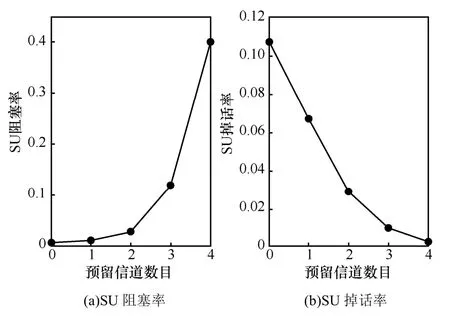
图12 以R为变量的阻塞率和掉话率

考虑到认知系统吞吐量作为阻塞率和掉话率的函数（由式(10)可知），对于不同的C值有唯一的R值与之对应，因此以最大认知系统吞吐量为目标，在满足业务对阻塞率和掉话率限制条件下，选取最优的R值是一个较为可行的方法，对此采用拉格朗日松弛法[19]进行求解。

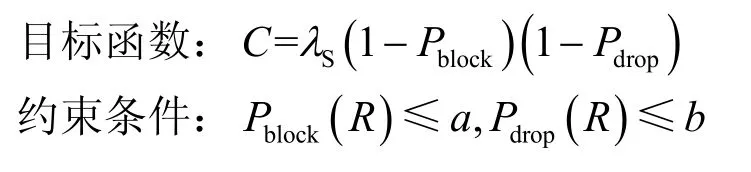
首先，给定拉格朗日乘子m和n，将约束条件松弛，得到拉格朗日函数

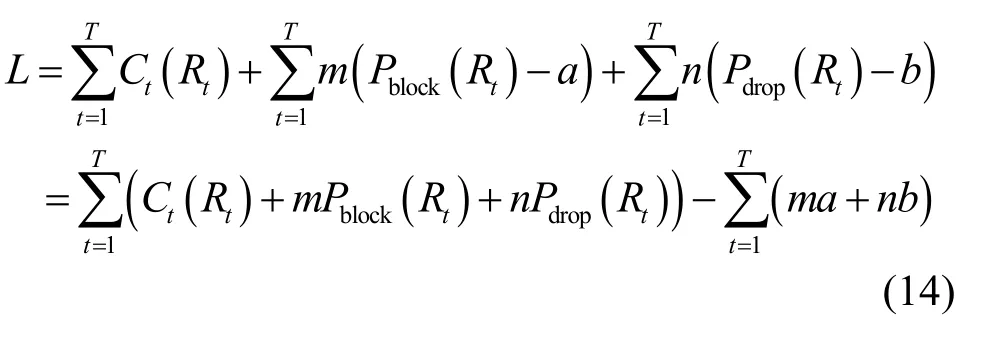
将式(14)分解为2层优化问题，分别进行求解。底层由T个子问题 Lt构成， t = 1,2,… ,T

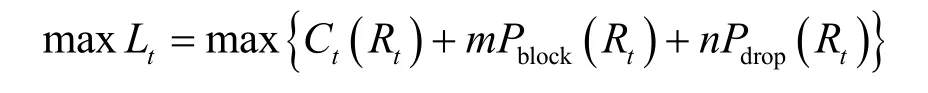
接下来，采用标准梯度法[19]修正拉格朗日乘子，在满足收敛条件时，获取原问题的最优解 Ropt及C的最大值。

1) 通过给定m、n的初值m0、n0，求得每个 Lt的最优解 Rt。

采用事件调度法进行求解的结果如图13所示，在为PU预留2个信道时，认知吞吐量达到最大值。此外，为PU预留0个信道时，该策略相当于基本频谱接入策略。结合图12和图13中可以看出为PU预留合适的信道有助于更多的SU完成服务，提高认知系统吞吐量。

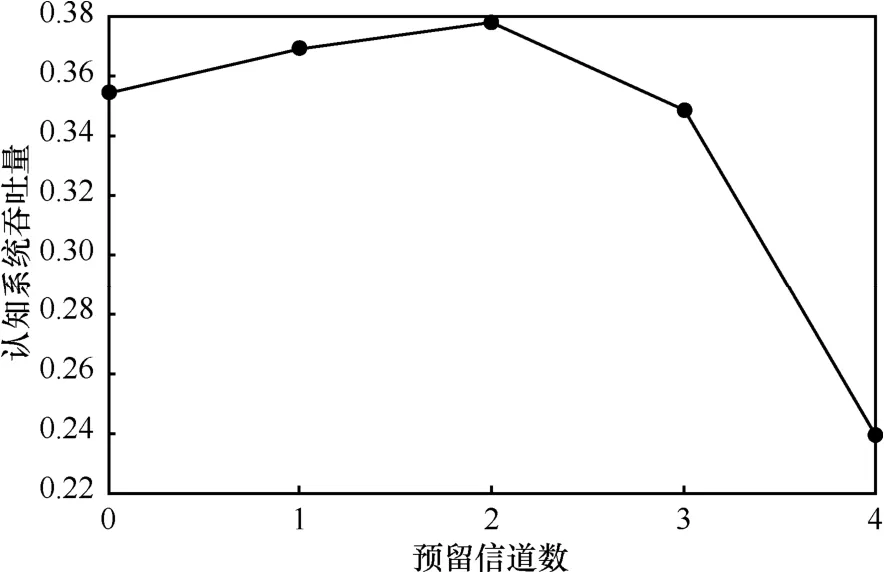
图13 以R为变量的认知系统吞吐量

4.3 不同业务对接入策略的选取

频谱切换接入策略使SU具有频谱切换能力，在可用频谱资源时变的情况下依然能维持正常通信。信道预留接入策略，通过改变信道分配政策，减少PU抢占SU信道的可能性，使得SU能顺利地完成服务。两者均以牺牲一定阻塞率获取较低的掉话率；相比之下，基本频谱接入策略则保持较低的阻塞率和较高的掉话率。3种接入策略各有优势，工作方式和应用场景有所不同，下面针对不同的业务类型选择最佳的频谱接入策略。

按业务接入性能的要求，将 3GPP和 IMTAdvanced定义的业务类型[20]划分为尽力而为型业务和实时型业务。

1) 尽力而为型业务

尽力而为型业务包括交互式业务和背景类业务，它们对阻塞率、掉话率要求严格，对频谱切换概率无限制。因此，阻塞率、掉话率成为该业务选择接入策略需要考虑的因素。

认知系统吞吐量是阻塞率和掉话率的函数，可以此为优化目标，在满足阻塞率和掉话率的限制条件下，选取最佳的接入策略。仿真参数设置如下：λp=0.3个数/s，λs=0.4个数/s，由4.2节的求解结果可知，R= 2 时信道预留接入策略的认知系统吞吐量最大，因此本节令 R = 2 。如图14所示，频谱切换接入策略的认知系统吞吐量最大，SU能完成更多的业务，因此，对尽力而为型业务而言是最佳的接入策略。

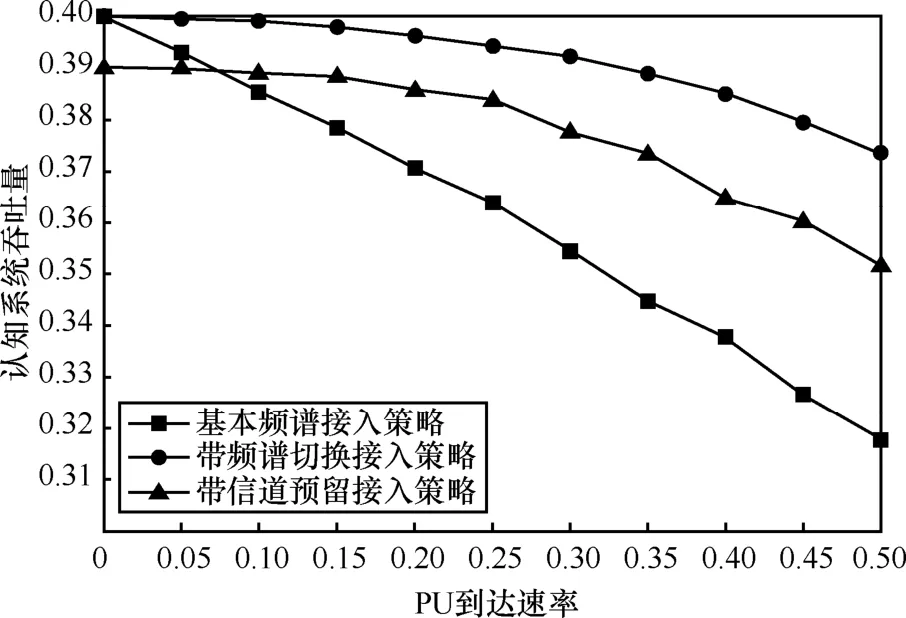
图14 以λp为变量的认知系统吞吐量

2) 实时型业务

实时型业务包括语音业务和媒体流业务，这些业务对掉话率、切换概率要求严格，对阻塞率要求较低。在选择最佳接入策略时需综合考虑这3个因素，将阻塞率、掉话率、切换概率分别加权求和，记作QoS效用函数U，U值越小，系统性能越优。

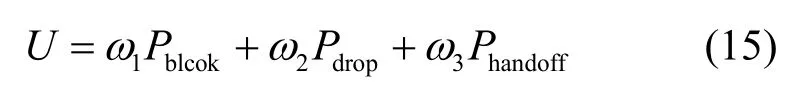
其中， ω1+ω2+ω3=1。考虑到阻塞率和掉话率对系统性能影响比较大，切换概率则对系统性能影响较小，并且实时型业务对各个指标的要求不同，设ω1=0.3，ω2=0.5，ω3=0.2，其他参数设置与图14一致。在上述参数下的QoS效用函数如图15所示，PU到达速率在0～0.1之间时，采用频谱切换接入策略的 U值最小；在0.1～0.5之间，采用信道预留接入策略的U值最小。因此，对实时型业务而言，当PU业务量较小时，选择频谱切换接入策略系统的性能最佳，当PU业务量较大时，选择信道预留接入策略系统的性能最佳。

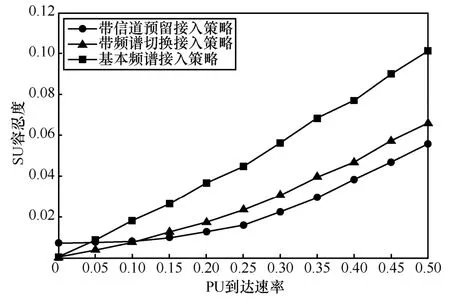
图15 以λp为变量的用户容忍度

5 结束语

本文讨论了文献[9]和文献[10]CRN接入模型中存在的问题，通过模拟PU和SU的行为重新进行建模，根据此模型修正了认知系统性能评估的重要指标的定义和表达式。采用矩阵几何法和离散系统仿真的事件调度法求得各状态的稳态概率，进一步重新评估了 CRN性能。理论分析和仿真结果一致，验证了所提的数学模型的可靠性。实验结果表明，频谱切换和信道预留接入策略，均以牺牲阻塞率换取掉话率，最大限度地维持SU服务；此外，频谱切换接入策略具有较高的信道利用率。针对不同业务类型的各性能指标的要求，选择最佳的接入策略，尽力而为型业务采用频谱切换接入策略；实时型业务在PU业务量较小时采用频谱切换接入策略，反之则采用信道预留接入策略。

附录

2.1节提到频谱切换技术给CRN接入带来一定的延迟，下面通过一组仿真实验说明延迟对系统性能的影响很小，可忽略不计。

假定仿真时间T=90 000s，N=5，p0～0.5=λ个数/s，λs= 0.4个数/s，（延迟时间为服务时间0.3倍）和D=0（无延迟）下，以λp为变量查看阻塞率和掉话率的变化情况。

如图16和图17所示，在相同参数下有延迟和无延迟的阻塞率和掉话率随 λp呈现相同的变化趋势，并且两者之间相差不到 0.5%。因此，可知频谱切换对系统性能的影响很小，可忽略不计。

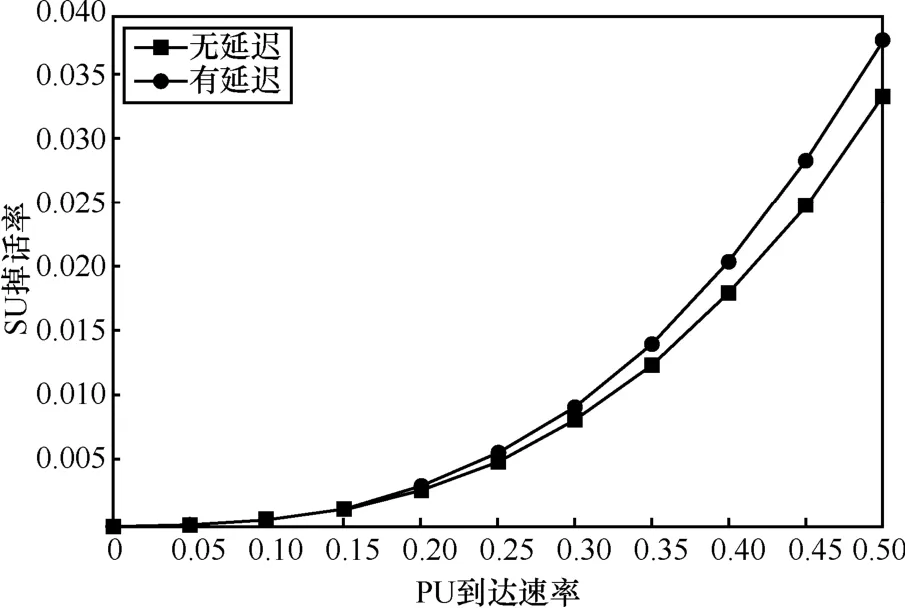
图16 以λp为变量的阻塞率

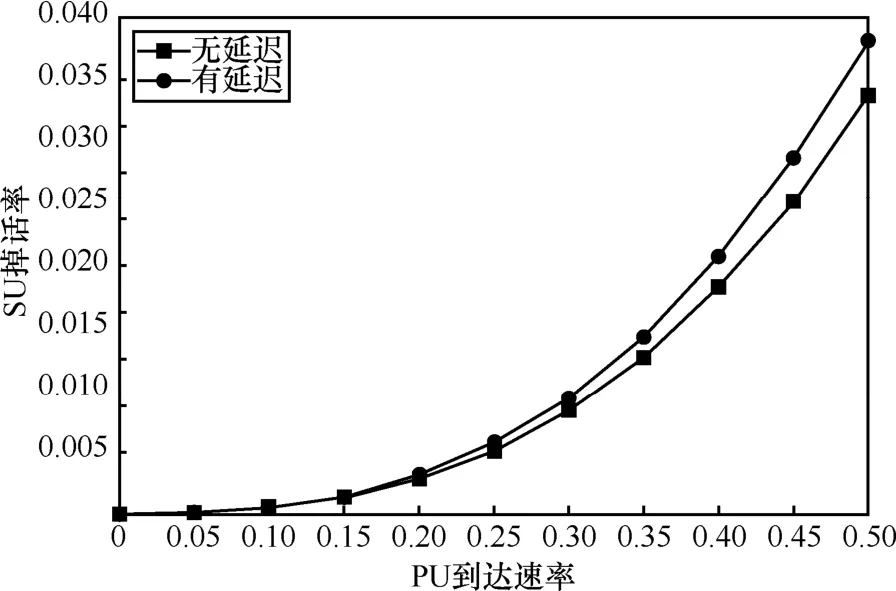
图17 以λp为变量的掉话率

[1] NTIA U S. Frequency allocations[EB/OL]. http://www.nita.doc.gov/osmhome/allochrt.pdf, 2010.

[2] MITOLA J. Cognitive Radio: An Integrated Agent Architecture for Software Def i ned Radio[D]. Sweden: Royal Institute of Technology(KTH), 2000.

[3] FRANK H P F, MARCOS D K. Cooperative and Cognitive Networks:A Motivating Introduction[M]. Springer, Netherlands, 2007.

[4] ARSHAD K, MOESSNER K. Collaborative spectrum sensing for cognitive radio[A]. Communications Workshops, 2009 ICC Workshops 2009. IEEE International Conference[C]. Dresden, Germany,2009. 1-5

[5] ZHANG L, ZHENG G X. Adaptive QoS-aware channel access scheme for cognitive radio networks[J]. Intenational Journal of Ad Hoc and Ubiquitous Computing, 2010, 6(3):172-182

[6] EDWARD P C K. An Introduction to Stochastic Processes[M]. Beijing: China Machine Press, 2003.

[7] WANG B B, ZHU J, LIU K. Primary-prioritized Markov approach for dynamic spectrum allocation[J]. IEEE Transactions on Wireless Communication, 2009,8(4):1854-1865 .

[8] 周来秀, 贺建军. 感知无线网络中频谱检测与动态接入技术研[D].长沙: 中南大学, 2008.ZHOU L X , HE J J. Research on Spectrum Sensing and DynamicSpectrum Access in Cognitive Radio Networks[D]. Changsha :Central South University, 2008.

[9] TANG P, CHEW Y, ONG L. Performance of secondary radios in spectrum sharing with prioritized primary access[A]. Military Communication Conference[C]. New York, USA, 2006. 1-7.

[10] KONDAREDDY Y R, ANDREWS N, AGRAWAL P. On the capacity of secondary users in a cognitive radio network[A]. Sarnoff Symposium[C]. Sarnoff Symposium, 2009. 1-5.

[11] 刘红杰, 李书芳. 基于认知无线电的动态频谱管理理论及相关关键技术的研究[D]. 北京:北京邮电大学, 2009.LIU H J, LI F S. Research on Theory and Related Key Techniques in Dynamic Spectrum Management Based on Cognitive Radio[D]. Beijing :Beijing University of Posts and Telecommunications,2009.

[12] LIANG Y H, CHANG B J, HSIEL S J. Analytical model of QoS-based fast seamless handoff in IEEE 802.16j WiMAX networks[J]. Vehicular Technology, 2010, 59(7):3549-3561.

[13] AHMED W, GAO J. Comments on “analysis of cognitive radio spectrum access with optimal channel reservation”[J]. IEEE Transactions on Wireless Communications, 2009, 8(9):4488-4491.

[14] HONG C P T, KANG H S, KOO I. An efficient radio resource management scheme for cognitive radio networks[J]. Advanced Intelligent Computing Theories and Applications, with Aspects of Artificial Intelligence Lecture Notes in Computer Science, 2010,6(21):376-383.

[15] NEUTS M F. Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach[M]. Baltimore: the John Hopkins University Press, 1981.41-66.

[16] WALLACE V. The Solution of Quasi Birth and Death Processes Arising from Multiple Access Computer Systems[M]. Michigan: Ph.D.Dissertation, Systems Engineering Laboratory, 1969.

[17] 田乃硕,岳德权.拟生灭过程与矩阵几何解[M].北京:科学出版社，2002.TIAN N S, YUE D Q. Quasi-Birth-Death Process and the Matrix Geometric Solution[M]. Beijing: Science Press,2002.

[18] 赵彤宇, 张乃通. 基于事件触发的通信业务量仿真方法[J]. 通信技术, 2002, 11(25):70-72.ZHAO T Y, ZHANG N T. Communication traffic simulation method based on event-triggering[J]. Communications Technology, 2002, 11(25):70-72.

[19] AHUJA R K. Network Flows: Theory, Algorithms and Applications[M]. Prentice Hall/Pearson, 1991.

[20] 惠蕾放,李建东.无线网络中兼顾业务类型及公平性的无线资源共享问题研究[J]. 通信学报, 2011, 32(4):39-46.HUI L F, LI J D. Radio resource sharing for wireless networks with traffic type and fairness consideration[J]. Journal on Communications,2011, 32(4):39-46.