基于直觉模糊c均值聚类核匹配追踪的弹道中段目标识别方法

雷阳，孔韦韦，雷英杰

(1. 武警工程大学 电子技术系网络与信息安全武警部队重点实验室，陕西 西安 710086；2. 武警工程大学 通信工程系，陕西 西安 710086；3. 空军工程大学 防空反导学院，陕西 西安 710051）

1 引言

弹道导弹自问世以来，以其射程远、威力大、精度高和生存能力强等优点成为战争中的“杀手锏”。作为对立面，弹道导弹防御系统应运而生。从20世纪60年代起，其研究热点几经调整，从对再入段“大气过滤”拦截的研究，到对天基助推段拦截的研究，直至近年来对大气层外中段拦截的研究，而如何解决目标识别一直是其核心难题之一。目前美国对国家导弹防御系统(NMD, national missile defense)有效性的怀疑也集中在对真弹头的有效识别上，因此目标识别问题仍是困扰NMD系统发展的一个“瓶颈”。

支撑向量机、相关向量机及核匹配追踪是近年来新兴的3种机器学习方法[1]，而核匹配追踪的提出为模式识别领域提供了一种崭新有效的核机器方法，它将某些在低维空间线性不可分的问题转化为高维空间线性可分的问题以期实现解决，核匹配追踪分类器的分类性能与支撑向量机基本相当，但却具有更为稀疏的解[2]，因而核匹配追踪的起步期发展已成功应用于目标分类[3]、图像识别[4～6]、雷达目标识别[7]、特征模式识别[8]、人脸识别、数据挖掘等领域。

虽然核匹配追踪的优良特性已成功服务于目标识别，但在处理大量数据集时，KMP为了在高度冗余函数字典中选取最佳匹配的数据结构，每一步搜索过程都需进行全局最优搜索，必然导致学习时间过长。而基于目标函数的 IFCM[9]这一局部最优的动态聚类算法，可通过多次修正聚类中心、直觉模糊划分隶属矩阵和直觉模糊划分非隶属矩阵进行动态迭代，可将粗糙的数据集分割成几个小型的字典空间进行局部搜索，从而减少了学习时间，降低了计算复杂度。因此，本文汲取IFCM算法的动态聚类优势，尝试将KMP算法中的核函数字典划分成若干个小型字典，从而进行局部搜索，克服全局最优搜索所致过长时间的学习过程。

在弹道导弹防御系统中段，目标飞行过程较之助推段、再入段，具有较长的识别及拦截时间，因此，导弹防御系统把更多的力量集中在中段，它被认为是导弹防御的关键阶段。但是由于没有大气阻力，诱饵、碎片、干扰物与真弹头的飞行速度是一致的，这给目标识别系统带来了极大的困难。高分辨一维距离像是目标散射点子回波在雷达射线上投影的向量和，可提供目标散射点的强度和位置信息，反映目标的形状和结构等特征。相对雷达目标像，HRRP更容易获取。因而本文选取HRRP这一弹道中段的常用特征属性，并对其进行特征子像提取，将所获得的数据用于进行目标识别。

本文的研究目的是将KMP与IFCM有效结合，用于进行HRRP特征子像数据的目标识别，为弹道中段目标识别提供一种新的尝试。鉴于此，本文提出了一种直觉模糊c均值聚类核匹配追踪的目标识别方法。首先，对UCI数据库中4组实际样本数据进行分类实验及有效性测试，验证 IFCM-KMP算法的有效性。其次，采用FCM，KMP，IFCM-KMP3种算法分别对真弹头进行目标识别仿真实验及结果对比分析，充分表明了 IFCM-KMP算法用于弹道中段目标识别较之FCM、KMP的优越性。

2 核匹配追踪算法

2.1 基本匹配追踪

给定 l个观测点{x1,…, xl}，相应的观测值为{y1,… yl}。基本匹配追踪(BMP, basic matching pursuit)的基本思想是：在一个高度冗余的字典(dictionary)空间D中将观测值{y1,…, yl}分解为一组基函数的线性组合来逼近yj(j=1～l)，其中，字典D是定义在Hilbert空间中的一组基函数[10,11]。假定字典包含 M个基函数： D = { gm}, m = 1 ,2,… , M 。对观测值yj(j=1～l)逼近的基函数向量的线性组合函数为

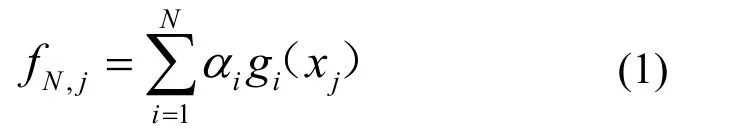
基本匹配追踪算法在每一步的优化迭代中，针对当前残差寻找与之相关系数最大的基函数Nmg 及其系数αN，观测值在第N代的逼近为

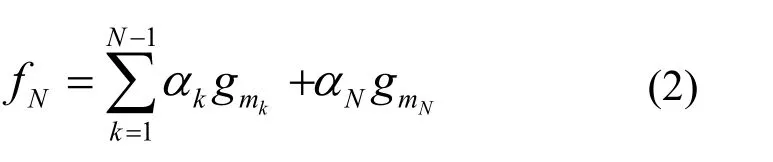
然而，当增加 αNgmN后，匹配追踪在第N代对观测值的逼近并一定是最优的；可以通过后拟合的方法修正fN，使其进一步逼近观测值[12]。所谓后拟合，就是增加 αNgmN项后，重新调整系数 α1,α2,…,αN,使得当前的残差能量最小，即

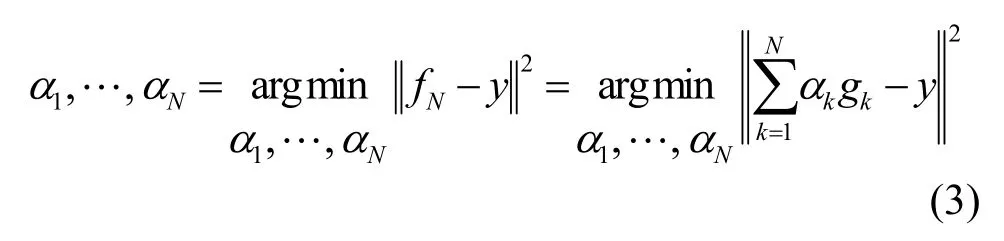
上式的优化过程是一个非常耗时的计算，通常采用折中的方法：匹配追踪算法在迭代运算数步后进行一次后拟合[11]。

2.2 核匹配追踪

核匹配追踪本质是采用核方法生成函数字典，它是一种利用核函数集进行寻优的匹配追踪方法，在 BMP算法的基础上，给定具体的核函数来代替函数 g，进而寻找权系数 ωi和基函数数据 xi，从而得到有效地分类器，再利用训练得到的分类器对目标进行分类识别。

假设L={(x1, y1),…,(xl, yl)}是一个含有l个输入输出，从一个未知的分布中独立采样出的数据对，基于训练数据的核函数集且考虑到常数项，则逼近函数可表示为

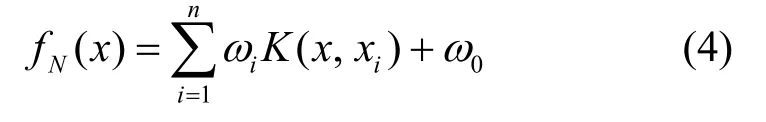
其中，xi是分类器基函数数据，训练过程是以L={(x1,y1),…,(xl, yl)}为训练集的有限维数据空间。

3 基于目标函数的直觉模糊 c均值聚类核匹配追踪算法

在处理大量数据集时，KMP为了在高度冗余的函数字典中选取最佳匹配的数据结构，每一步搜索过程都需进行全局最优搜索，因此KMP的学习时间是相当长的。因而结合基于目标函数的IFCM这一局部最优的动态聚类算法，通过多次修正聚类中心、直觉模糊划分隶属矩阵及直觉模糊划分非隶属矩阵进行动态迭代，可将核函数字典分割成几个小型的字典空间进行局部搜索，减少计算时间，降低计算复杂度。

3.1 IFCM-KMP算法及步骤

下面给出IFCM-KMP算法的详细步骤。

输入：样本数据集L={(x1, y1),…, (xl, yl)}，平滑参数 m(1＜m＜∞)，核参数 σ (σ≥0)，聚类类别数 c (2≤c≤n)。

输出：划分直觉模糊隶属矩阵Uμ，划分直觉模糊非隶属矩阵 Uγ，聚类原型 P，迭代次数 b、N，多个小型函数字典 D={d1,…, dc}，最优权系数 ωj和基函数数据，判决函数ft。

Step1 初始化。核函数K，此处选取高斯核函数K(x, xi)=exp(-‖x-xi‖2/2σ2)，设定核参数为直觉模糊聚类区间C的个数。计算样本数据个数n，设定迭代停止阈值ε、ηt，初始化聚类原型模式P(0)，设置迭代计数器b=0。

Step2 对于数据集X ={x1,…, xl}，利用IFCM算法计算更新聚类原型模式矩阵pi(b+1)，由于该聚类原型矢量pi(b+1)各维特征上的赋值是一直觉模糊数，需分别进行最优化从而得到其划分直觉模糊隶属矩阵 Uμ和划分直觉模糊非隶属矩阵 Uγ的迭代式(5)、式(6)，并求得 pμi(b+1)和 pγi(b+1)。在直觉模糊集中，已知隶属度与非隶属度可易得犹豫度，因此其迭代公式可通过式(5)、式(6)易得，如式(7)所示，并求得 pπi(b+1)。

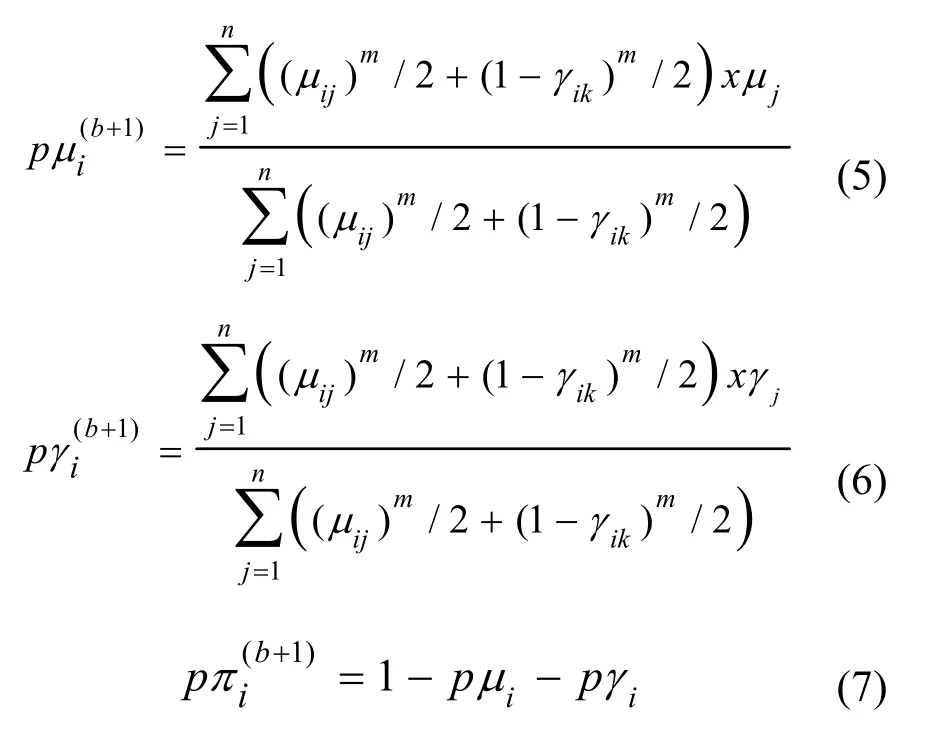
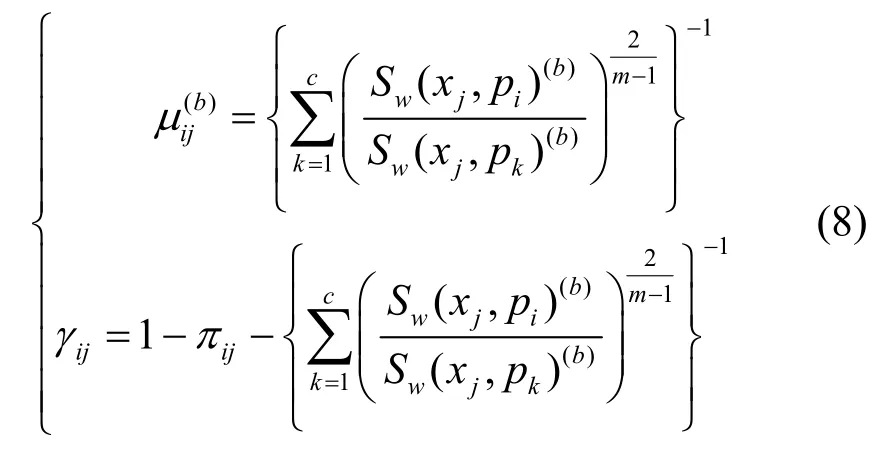
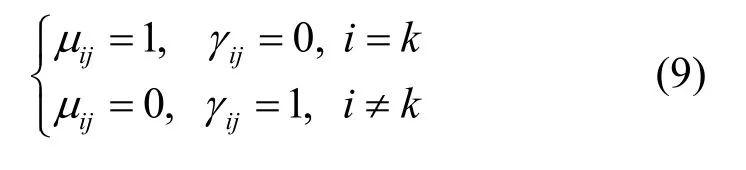
Step4 确定最优权系数ωj和基函数数据。从训练数据集中选 xi=x1，求出 y1(x)=K(x,x1)，利用极小值准则求出（本质上是一个求解最小二乘解问题），然后求出依次选xi=x2,…, xl，求出 Δy2, …, Δyl，取 Δy1, …, Δyl中最小的所对应的xi作为第一个基函数数据。

Step5 假设已求出L个权系数和基函数数据，利用 KMP思想，则第 L+1个求法如下：令采用 Step4中方法确定第L+1个基函数数据，进而对 yL进行一次后拟合：，j=1, 2, …, L+1，其中，

Step6 按照Step4、Step5依次计算D={d1, …,dc}中每个小型函数字典dj(j=1, …, c)的ωj，和，从核函数集中选取最小△yj所对应的ωj，和。

Step7 按照下式计算判决函数。

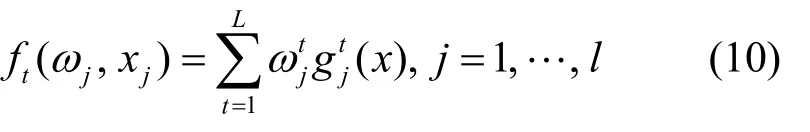
Step8 令 y=y-ft，若‖y‖≤ηt，则返回 Step4，且每一个dj的迭代次数N增大，直至算法收敛。

最后得到分类器ft后，目标可通过下式进行分类获得

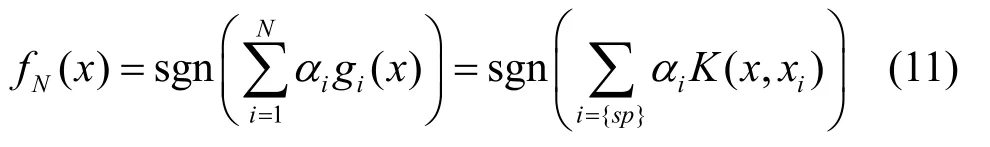
其中，{sp}表示核匹配追踪算法得到的支撑模式。

该算法涉及平滑因子参数m的数值选取。从数学角度看，参数m的出现并不自然且没有必要，但是对于从硬聚类准则函数推广得到的目标函数模糊聚类准则函数，如果不给隶属度赋一个权重，这种推广则是无效的。因而参数m又称为加权指数，控制着样本在模糊类间的分享程度。因此，要实现模糊聚类就必须涉及 m的数值选取，然而最佳 m的选取目前尚缺乏理论指导。参数m的取值范围大都来自实验及经验，均为启发式的，缺乏系统性，更无具体的优选算法及检验算法可循。这一系列的开放性问题，都值得进一步的探索，以便奠定m优选的理论基础。通常情况下选取m=2。

该算法也涉及核函数参数σ的选取。解决方法是先将数据集分为3组，分别是训练数据集、验证数据集和测试数据集。其中，训练数据集用于训练分类器，测试数据集用于评估分类器的性能，而验证数据集则是用于确定核参数σ的。实验验证是对给定的一组数据，将其分为2组，一组作为验证数据，一组作为测试数据，而训练数据是从验证数据中提取平均距离像得到的，这是由于平均距离像具有较好的目标方向变化稳定性，可以保证识别器具有良好的推广能力。

结论：总的来说，在日常使用pH计的过程中，一定要注重细节，规范程序，区分不同类型，注意pH计相关的校准和温度补偿等环节。

该算法输入的样本数据集 L={(x1, y1), …, (xl,yl)}，Y∈{-1, +1}是一个2类分类问题，当样本数据集为多类分类问题时，通常有2种解决方法：第一种方法把N类分类问题转化为N个2类分类问题，其中，第i个问题是把属于第i类和不属于第i类的分开，这种方法需要N个分类器；第2种方法是直接把这 N 类进行两两判决，即每两类就需要一个分类器进行一对一的判决，这种方法需要N (N -1) /2个分类器。为了减少计算复杂度，以下仿真实验均采用第一种方法通过训练N个分类器联合进行分类。

3.2 IFCM-KMP分类实验及有效性测试

选取 UCI数据库(http://www.ics.uci.edu/～mlearn/MLRepository.html)中 3组实际样本数据Iris，Wine，Breast Cancer Wisconsin(简记为 Wisc)及UCI库外其他实际数据Motorcycle，以上4组实际数据通常被用来检验聚类算法、分类算法的性能及有效性。Iris数据是由4维空间的150个样本组成，每一个样本的4个分量分别表示Iris数据的petal length、petal width、sepal length、sepal width。该数据共有3个种类setosa、versicolor、virginica，每一个种类均有50个样本。Motorcycle为一组实际生活中低维简单数据，共有134个样本数据，每个样本具有 3个不同特征属性。Wine和 Breast Cancer Wisconsin 2类样本数据的特征属性此处不再赘述。基于以上4组数据分别对FCM、KMP、IFCM-KMP算法的分类性能进行仿真实验。

选取Iris数据对IFCM-KMP算法进行仿真实验。实验中选取高斯核函数K(x, xi)=exp(-‖x- xi‖2/2σ2)，且设定核参数σ2=0.03，平滑参数m=2，聚类类别数(即样本种类数)c=3，样本数据个数 n=150，迭代停止阈值 ε=10-5、ηt=0.2，设置迭代计数器 b=0。Iris数据是由3个不同种类的150个样本组成，且每个样本是基于4个连续属性的，其原始样本分布为第1个种类与其他2类完全分离，第2个种类与第3个种类之间有交叉。3个种类在图 1中分别表示为“·”、“○”和“×”。采用IFCM-KMP算法进行分类时，由于Iris数据样本均是分布在4维空间中的，其分类效果通过4维或者3维空间都不易观察，因此将其映射到2维空间，产生PCA图对其分类样本的分布效果进行展示，如图1所示。由图清晰可见IFCM-KMP算法将3类样本明晰地分离开来，使得Iris样本中任意2类样本数据几乎没有交叉分布。

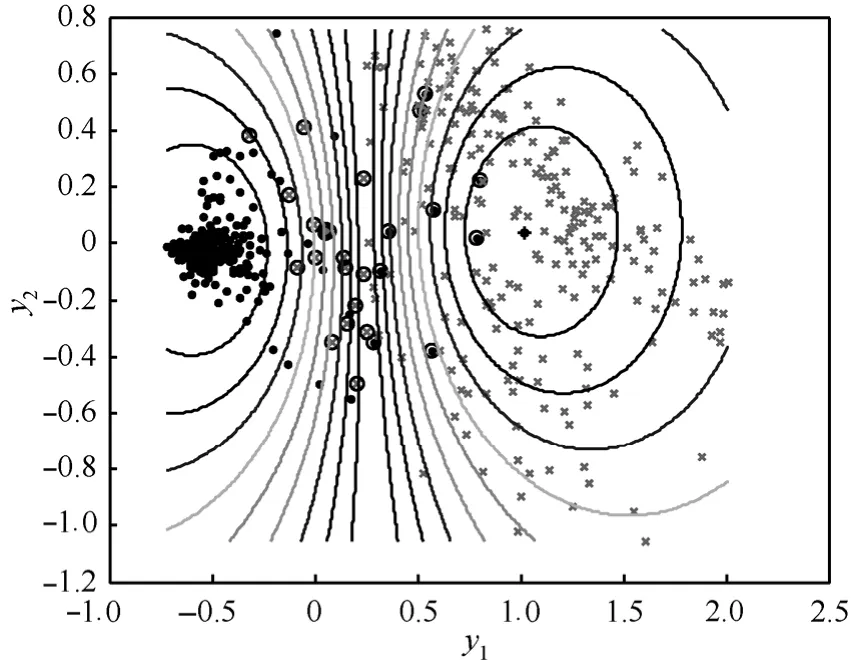
图1 Iris数据的IFCM-KMP 2维空间PCA映射

由于各参数设置不同，分类后的样本分布及错分误差也会不同，因而该算法的平均错分误差仅为ε1=0.031 1。同时采用FCM、KMP、IFCM-KMP算法分别对 Iris、Wine、Breast Cancer Wisconsin和Motorcycle 4组数据进行仿真实验，表1给出以上3种算法在相同实验平台下选取100次不同参数的平均错分误差。由表1可知IFCM-KMP算法的分类识别效果最好，KMP算法分类识别效果次之，FCM算法较之其他2种分类效果最差。

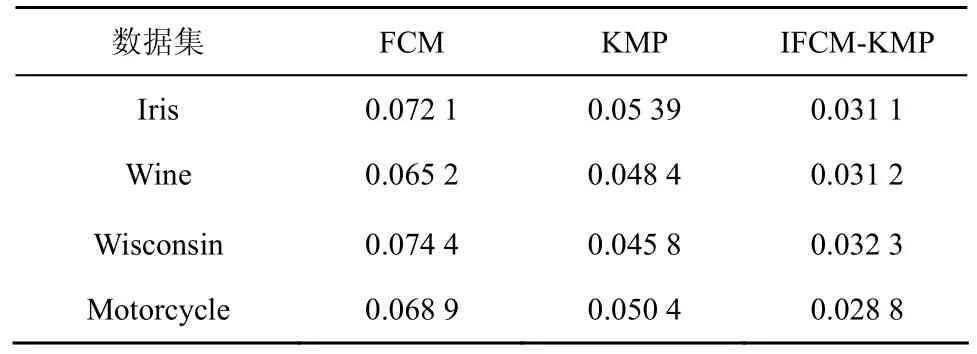
表1 3种算法的平均错分误差值

选取Motorcycle样本数据对该算法的有效性进行测试。在处理Motorcycle的134个样本数据时，首先采用IFCM算法将核函数分割成几个小型的字典空间并进行局部搜索，同时通过多次不断地修正聚类中心、划分直觉模糊隶属矩阵及划分直觉模糊非隶属矩阵进行动态迭代，如图 2所示，“·”和“*”分别表示样本数据和局部最优动态聚类点，经过数次迭代得到不同的局部最优动态聚类点，最后一次迭代得到的局部最优动态聚类点分布如图 2所示。此外，每次迭代会产生不同的7项有效性指标值(partition coefficient(PC)、classification entropy(CE)、partition index(SC)、separation index(S)、xie and beni’s index(XB)、dunn’index(DI)，alternative dunn index(ADI))。为比较FCM、KMP和IFCM-KMP算法的有效性能指标，3种算法均选取 Motorcycle样本数据进行实验，分别取最后一次迭代所得的 7项性能指标值如表2所示。

图2 局部最优动态聚类中心点分布

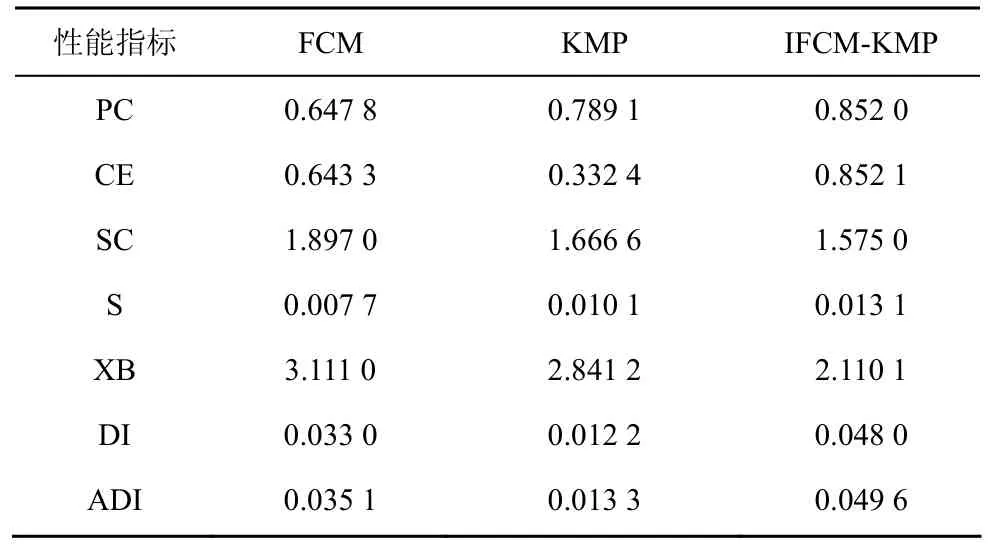
表2 Motorcycle数据的3种算法有效性指标比较

由表2中各项数据可知，该算法的PC值略大于FCM、KMP的PC值，说明该算法具有比其他2种算法更好的划分性能；FCM、IFCM-KMP算法的CE值均较为接近各PC值，说明它们均具有较好的模糊聚类划分性能，而KMP算法的CE值与其PC值相差较大，说明KMP算法模糊聚类划分性能较弱；该算法的SC值略低于FCM、KMP的SC值，说明该算法划分得到的聚类比FCM、KMP划分得到的聚类更具紧密性；相反的，该算法的S值则略高于FCM、KMP的S值，说明被FCM和KMP划分后的聚类数据样本之间的分离度大于 IFCM-KMP划分后的聚类数据样本；该算法的XB值略小于FCM、KMP算法的XB值，说明其局部搜索、动态聚类的性能较强；该算法的DI值略大于FCM、KMP算法的DI值，说明其兼顾紧密性与分离度的能力更好；ADI指标的作用是对DI指标进行修正，用更简单的计算方式将其值增大，3种算法均达到了增大各 DI值的效果。根据比较各算法的性能指标值可知，IFCM-KMP算法是有效的。

4 直觉模糊 c均值聚类核匹配追踪目标识别的仿真实验及分析

4.1 弹道中段目标识别

弹道导弹防御系统是指反洲际弹道导弹(ICBM,intercontinental ballistic missile)与反战术弹道导弹(TBM, tactical ballistic missile)，洲际弹道导弹与战术弹道导弹这2种导弹的基本飞行过程与模型体系相类似，均可在助推段、中段和再入段实现目标识别与拦截。在助推段(固体洲际导弹飞行时间在80～200s，液体洲际导弹飞行时间在 4～5min)，诱饵尚未放出，拦截虽无需进行真假目标识别，又可形成一种攻势防御，但拦截技术难度较大，往往难以实现。在再入段(持续时间不到 1min)，大气的过滤作用使目标识别相对容易，但拦截时间短，风险大，且很难做到一次精准拦截，一般须多层拦截，导致代价过大。在中段(飞行时间为20min或更长)，目标飞行具备较长的识别及拦截时间，因此，导弹防御系统把更多的力量集中在中段，它被认为是导弹防御的关键阶段。但是由于没有大气阻力，诱饵、碎片、干扰物与真目标飞行的速度是一致的，这给目标识别系统带来了极大的困难。目前在弹道导弹中段，雷达识别是主要途径，而根据所提取特征，识别方法大致分为3种[13]，分别是基于诱饵释放过程的识别方法、基于姿态特性的识别方法和基于结构特性的识别方法。而高分辨一维距离像是目标散射点子回波在雷达射线上投影的向量和，可提供目标散射点的强度和位置信息，反映目标的形状和结构等特征。相对基于雷达目标像，HRRP更容易获取。根据HRRP这一目标特征，本文方法属于基于结构特性的目标识别方法。

4.2 基于IFCM-KMP弹道中段目标识别的仿真实验及分析

弹道中段目标识别是在各种轻重诱饵(假目标)、末级运载火箭碎片及其他干扰物中识别真弹头。本文以锥球体所代表的弹头目标为例进行仿真实验，采用的数据(真弹头、假目标、碎片、干扰物)均是在微波暗室中对各类目标的缩比模型测量得到的。目标具体参数如下：总长60mm，直径140mm，锥角13.4°；雷达采用步进扫频测量方式，工作频率范围为 8.75～10.75GHz，步长 20MHz；目标横滚角和俯仰角均为0°，方位角范围是0～180°，平均方位角采样间隔为0.47°。该数据是121维的，各类样本数分别为65、77、58、50。实验中，采用等间隔从每类中选取一半作为训练数据，其余作为测试数据。

实验中，先提取数据特征子像。图3为弹道中段4类测试数据子像的空间散布，其中，“○”、“□”、“◇”、“*”分别表示假目标、碎片、干扰物、真弹头的子像。由图3可知，各类子像间存在个别混叠现象，说明FKOT-CC算法能提取可分性较强的鉴别特征，其中微小的差别主要是由计算误差引起的。

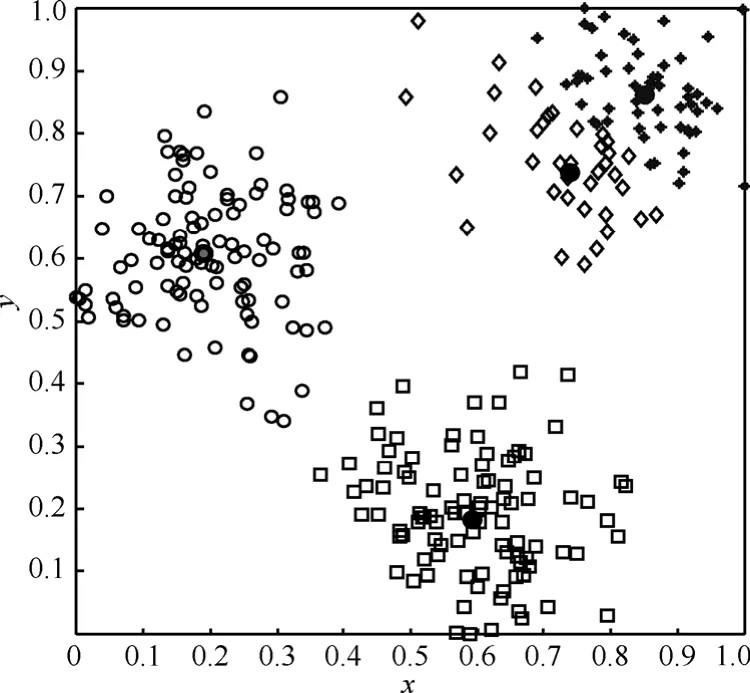
图3 微波暗室数据的子像散布

针对以上各类子像进行IFCM-KMP分类仿真实验。选取高斯核函数 K(x, xi)=exp(-‖x-xi‖2/2σ2)，且设定核参数σ2=0.03，平滑参数m=2，聚类类别数(即样本种类数)c=4，样本数据个数n=250，迭代停止阈值ε=10-5、ηt=0.2，设置迭代计数器b=0。图4为采用IFCM-KMP算法进行分类仿真实验且将其映射到2维空间的PCA结果分布图。针对各类子像分别采用 FCM，KMP算法进行分类仿真实验，同样得到图5、图6的2维映射结果展示。图4、图5、图6中，“⊕”、“⊗”、“·”和“×”分别表示假目标、碎片、干扰物、真弹头。显然，IFCM-KMP的分类效果最好，真弹头有效地被分离开来，其他3类样本也均聚集在各自聚类中心周围，错分误差ε1=0.233。KMP的分类效果较之IFCM-KMP次之，错分误差ε2=0.373。而 FCM 的分类效果最差，真弹头与假目标混叠样本较多，没有达到分离真弹头的效果，

错分误差ε3=0.741。

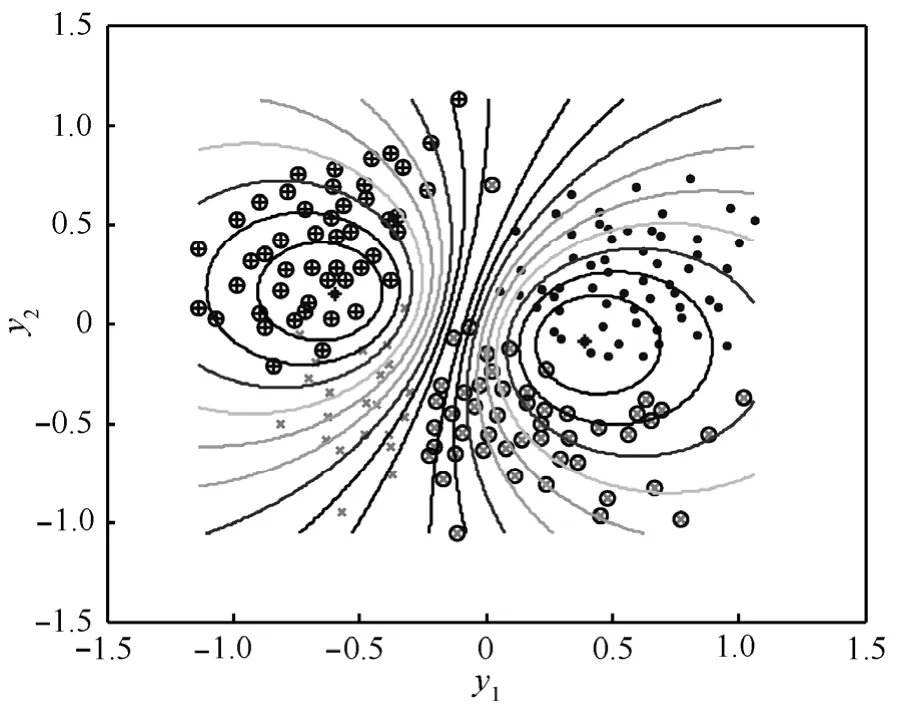
图4 各类子像的IFCM-KMP 2维空间PCA映射

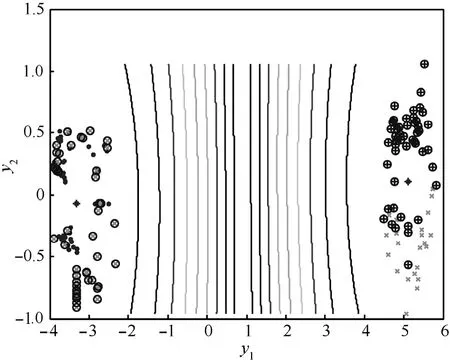
图5 各类子像的FCM 2维空间PCA映射

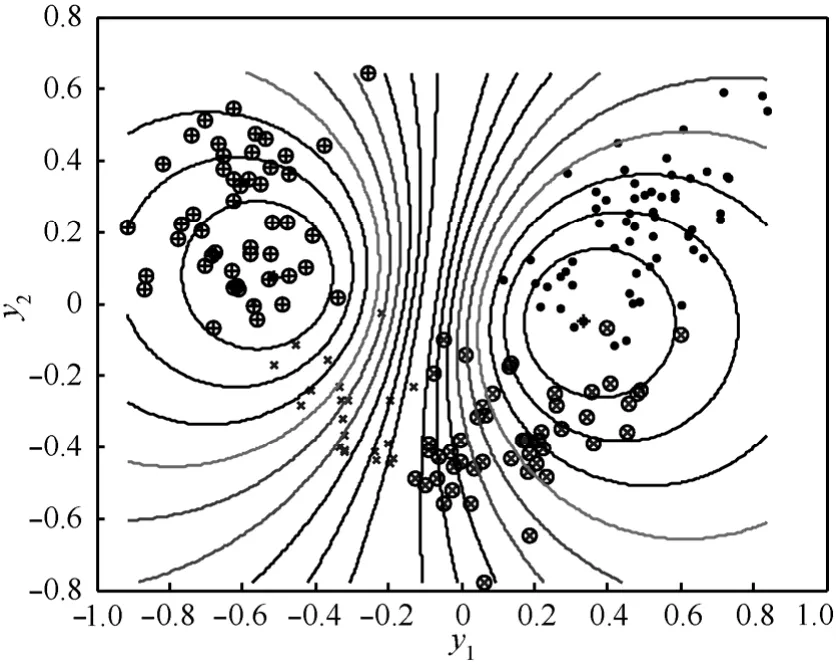
图6 各类子像的KMP 2维空间PCA映射

根据各参数设置的变化，各类样本分布及错分误差也会有所不同。表 3给出 FCM、KMP、IFCM-KMP 3种算法在相同实验平台下选取100次不同参数的平均错分误差及真弹头的平均识别率。由表3可知，IFCM-KMP对于真弹头的平均识别率较高，KMP次之，而 FCM 平均识别率最低。IFCM-KMP算法的运行速度较之FCM较慢，且在可承受的代价之内，但该算法较之 FCM 在分类性能上的明显优势，是经典 FCM 算法无法比拟的。该算法的运行速度是远远高于KMP算法的，可见该算法划分小函数字典进行局部搜索跳出KMP算法的全局搜索，确实有效地克服了全局搜索导致时间过长的缺陷。因此，较之KMP算法，该算法在时间复杂度及分类性能上都具有较大优势。因此，对于需兼顾识别效果及识别速度的弹道中段目标识别，IFCM-KMP算法不失为一种较好的选择。

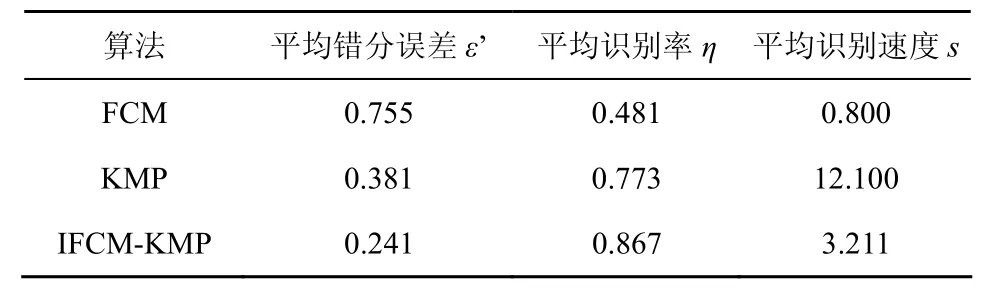
表3 3种算法的平均错分误差值、平均识别率及平均识别速度

5 结束语

本文的主要贡献是基于核匹配追踪这一理论，利用直觉模糊 c均值聚类算法的动态聚类优势将KMP算法中核字典划分成若干小字典并进行局部搜索，克服了KMP算法全局搜索的缺陷，大大地降低了算法复杂度，且得到了更好的分类识别效果。之后选取高分辨距离像这一弹道中段目标识别时常用的特征属性，通过对其进行特征提取获得子像，从而分别采用 FCM，KMP，IFCM-KMP 3种算法对真弹头进行目标识别仿真实验。仿真结果表明，虽然该算法的运行速度较之 FCM 较慢，且在可承受的代价之内，但该算法较之 FCM 在分类性能上的明显优势，是经典 FCM 算法无法比拟的。而较之KMP算法，该算法无论在时间复杂度及分类性能上都具有较大优势。因此，对于需兼顾识别率及时效性的弹道中段目标识别， IFCM-KMP算法不失为一种较好的选择。但该算法仍有一些需改进和完善的地方，如平滑因子m、核参数σ、停止阈值ηt的确定方法，选取不同参数对目标识别结果的影响以及在真实弹道中段复杂环境下(非仿真环境下)采用该算法对真弹头进行目标识别的分类效果均是下一步夯待探究的问题。

[1] POPOVICI V, BENGIO S, THIRAN J P. Kernel maching pursuit for large datasets[J]. Pattern Recgnition, 2005, 38(12):2385-2390.

[2] PASCAL V, YOSHUA B. Kernel matching pursuit[J]. Machine Learning, 2002, 48:165-187.

[3] LIAO X J, LI H, KRISHNAPURAM B. An M-ary kernel macthing pursuit classifier for multi-aspect target classification[A]. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP)[C]. Montreal, Canada, 2004. 61-64.

[4] 缑水平, 焦李成. 基于多尺度几何分析与核匹配追踪的图象识别[J].模式识别与人工智能, 2007, 20(6):776-781.GOU S P, JIAO L C. Image recognition based on multi-scale geometric analysis and kernel matching pursuit[J]. Pattern Recognition and Artificial Intelligence, 2007, 20(6):776-781.

[5] 缑水平, 焦李成, 张向荣. 基于免疫克隆与核匹配追踪的快速图象目标识别[J]. 电子与信息学报, 2008, 30(5):1104-1108.GOU S P, JIAO L C, ZHANG X R. Kernel matching pursuit based on immune clonal fast algorithm for image object recognition[J]. Journal of Electronics & Information Technology, 2008, 30(5):1104-1108.

[6] 缑水平, 焦李成, 张向荣. 基于免疫克隆的核匹配追踪集成图象识别算法[J]. 模式识别与人工智能, 2009, 22(1):79-85.GOU S P, JIAO L C, ZHANG X R. Image recognition with kernel matching pursuit classifier ensemble based on immune clone[J]. Pattern Recognition and Artificial Intelligence, 2009, 22(1):79-85.

[7] 马建华, 刘宏伟, 保铮. 利用核匹追踪算法进行雷达高分辨距离像识别[J]. 西安电子科技大学学报（自然科学版）, 2005, 32(1):84-88.MA J H, LIU H W, BAO Z. Radar HRRP recognition based on the kernel matching pursuit classifier[J]. Journal of Xi’an Electronic Technology University(Natural Science Edition), 2005, 32(1):84-88.

[8] 李青, 焦李成, 周伟达. 基于模糊核匹配追寻的特征模式识别[J].计算机学报, 2009, 32(8):1687-1694.LI Q, JIAO L C, ZHOU W D. Pattern recognition based on the fuzzy kernel matching pursuit[J]. Chinese Journal of Computers, 2009, 32(8):1687-1694.

[9] 申晓勇, 雷英杰, 李进. 基于目标函数的直觉模糊集合数据的聚类方法[J]. 系统工程与电子技术, 2009, 11(31):2732-2735.SHEN X Y, LEI Y J, LI J. A clustering technique to intuitionistic fuzzy sets based on objective function[J]. Systems Engineering and Electronics, 2009, 11(31):2732-2735.

[10] DAVIS G, MALLAT S, ZHANG Z. Adaptive time-frequency decompositions[J]. Optical Engineering, 1994, 33(7): 2183-2191.

[11] MALLAT S, ZHANG Z. Matching pursuit with time-frequency dictionaries[J]. IEEE Transactions on Signal processing, 1993, 41(12):3397-3415.

[12] PATI Y, REZAIIFAR R, KRISHNAPRASAD P. Orthogonal mathcing pursuit: recursive function approximation with applications to wavelet decomposition[A]. Proceedings of the 27th Annual Asilomar Conference on Signals, Systems and Computers[C]. CA, USA, 1993.40-44.

[13] 李康乐, 刘永祥, 黎湘. 弹道导弹中段防御系统目标识别仿真研究[J].现代雷达, 2006, 11 (28):12-19.LI K L, LIU Y X, LI X. A study on simulation of target discrimination in ballistic missile mid-course defense system[J]. Modern Radar, 2006,11(28):12-19.

[14] 赵峰, 张军英, 刘敬. 基于核最优变换与聚类中心的雷达目标识别[J]. 控制与决策, 2008, 23(7):736-740.ZHAO F, ZHANG J Y, LIU J. Radar target recognition based on kernel optimal transformation and cluster centers[J]. Control and Decision,2008, 23(7):736-740.