基于仿射和复合混沌的图像自适应加密算法

文昌辞，王沁，黄付敏，袁志树，陶春生

（1. 北京科技大学 计算机系，北京 100083；2. 中国医学科学院，北京 100005；3. 空军驻京昌地区军事代表室，北京 100009；4. 中国人民解放军驻二一八厂军事代表室，北京 100009）

1 引言

传统加密算法如DES、3-DES、IDEA、AES针对一维数据流而设计，没有考虑数字图像具有数据量大、相关性强、冗余度高的特点，加密效率不高，并且加密之后可能保留着物体的大致轮廓，因而不适用于加密数字图像。目前，数字图像加密主要有3种基本操作：1)置乱空域像素（或变换域系数）的位置；2)代换空域像素（或变换域系数）的值；3)在空域像素（或变换域系数）的值之间进行扩散。

使用以上3种操作（置乱、代换、扩散）在空域直接加密像素后，破坏了像素间的相关性，很难通过压缩编码算法进行压缩。它的优点是没有数据损失，能精确地恢复出明文，并且算法操作相对简单，不存在从空域映射到变换域的大量浮点运算。文献[1～8]没有综合运用置乱、代换和扩散3种操作，在明密文对中容易分析、构造出线性计算关系，因此安全性不高，算法容易被选择明文攻击破解出等效密钥。文献[1～4]都只置乱了像素的位置，没有代换和扩散。文献[5]改变了像素的值，但没有置乱像素的位置。文献[6]针对有限精度下单一混沌映射周期较短且易于破解的缺点，将 2个混沌系统串联起来，增强了混沌系统轨道的安全性；但是该算法采用了流密码的形式，在加密像图像这样的海量数据时，很难保证一次一密，而且它仅采用了与像素值相异或的代换操作，一对明密文即可破解出等效密钥。文献[7]提出了一种改变像素值的矩阵变换加密算法，没有改变像素的位置，通过选择明文求解同余方程组可以破解。文献[8]根据序列中元素的取值来控制图像进行自适应置乱，本意是想增强抵御选择明文攻击的能力，但由于缺少代换和扩散操作，自适应加密的优势没有得到发挥。文献[9]没有与明文相关的自适应操作，通过选择明文攻击可以破解出等效密钥；如果将图像数据通过一个不可逆的变换引入到加密过程中，就可能堵上这个漏洞。文献[10]对一个运用广义猫映射来加密图像的算法进行了分析，发现它虽然含有置乱、代换、扩散操作并且迭代多轮，但由于该算法中的置乱操作存在不动点而且代换和扩散操作比较简单，导致明密文中存在一定程度的线性计算关系，所以安全性不高，该文对其进行了破解。

由于计算机精度有限，基于变换（如 DFT、DCT、DWT、FRFT[11]、FRHT[12]、MPDFrRT[13]）域的加密算法在变换与反变换时存在数据精度损失，所以解密后的图像与明文不会完全相同。如果将从空域映射到变换域的浮点操作仅仅作为一个加密运算步骤[11～13]，而未将其结合到压缩编码中，那么所耗费的计算量就太大，加密效率很低。结合图像压缩的加密通常在变换域系数被量化后进行，这样可使压缩尽量不影响加密。此处不对基于变换域的加密算法作深入探讨。

基于有限整数域上的三维仿射变换和混沌，本文提出一种新的空域加密算法，先通过置乱变换打乱像素的位置并根据像素坐标混合像素值，然后依次进行非线性的扩散、代换、再扩散，代换时用图像当前数据扰动耦合的多个混沌系统以进行自适应加密，如此迭代3轮。

2 置乱变换

置乱变换可以快速地打乱像素位置，破坏图像中原有的相关性，把图像变得杂乱无章、无法识别，它既可以单独用于图像加密，也可以作为图像加密系统的一个功能部件。为了保证加密之后还能正确恢复，置乱变换必须可逆，即为一一映射。基于仿射变换、有限整数域上的二维非等长置乱变换和整数提升变换，定义有限整数域上的一种三维仿射变换，记为三维类仿射变换。通过对参数进行适当设置，该变换可以为一一映射。

定义1 定义三维类仿射变换为

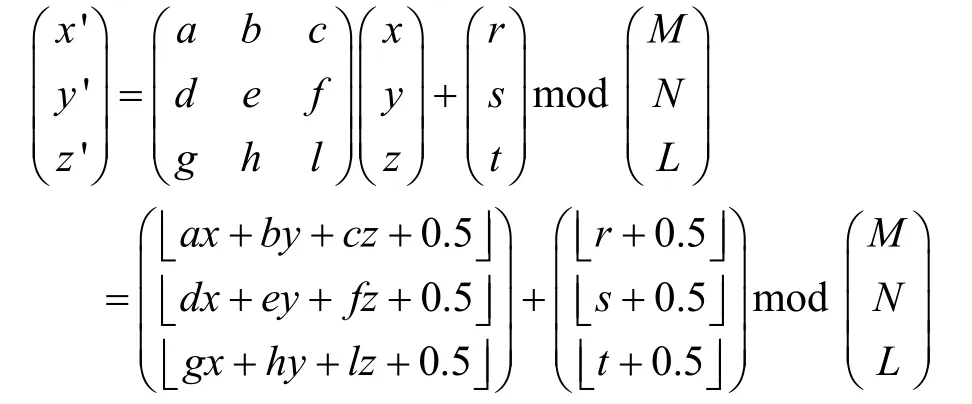
其中， a , b, c, d, e, f, g, h, l, r, s, t为实数， M , N, L为正整数， x, x', y, y', z, z'为非负整数且 x, x'∈ [ 0,M - 1 ],y, y'∈[0,N -1],z, z'∈[0,L-1]，表示取整运算。

在该变换中，对参数进行适当设置，可得到以下2个式子。

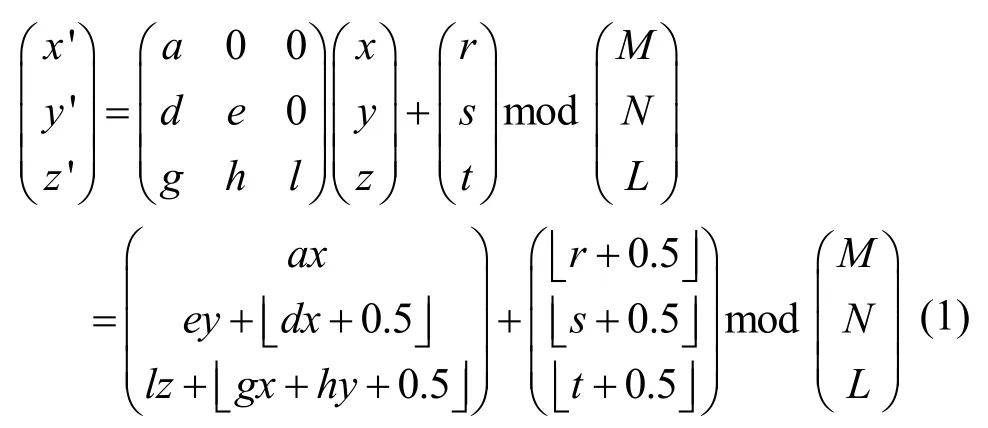
其中， a , e, l为非零整数且gcd(a, M ) =gcd(e, N)=gcd(l, L) = 1 ,d, g, h, r, s, t为实数。

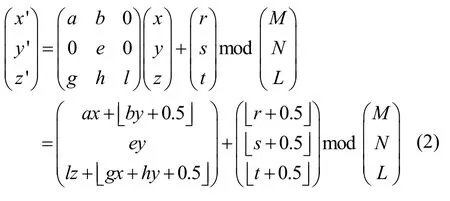
其中， a , e, l为非零整数且gcd(a, M ) = g cd(e, N)=gcd(l, L) = 1 ,b, g, h, r, s, t为实数。

可以证明，如果把式(1)，式(2)用于图像(M行N列)的置乱变换，其中(x, y, z)代表置乱前像素坐标和像素值，(x', y', z')代表置乱后像素坐标和像素值，那么该置乱变换是一一映射。

证明

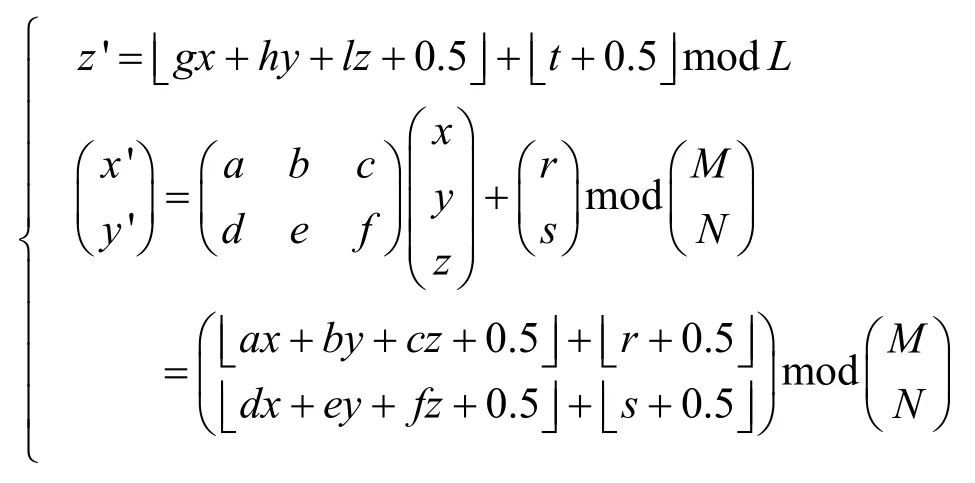
将三维类仿射变换改写为即将该变换分解为串行执行的2个操作：根据坐标混合像素值z得到 z ';置乱像素的坐标位置(x, y)到(x', y')。

2）取式（1）进行三维类仿射置乱时，像素坐标位置的变换为

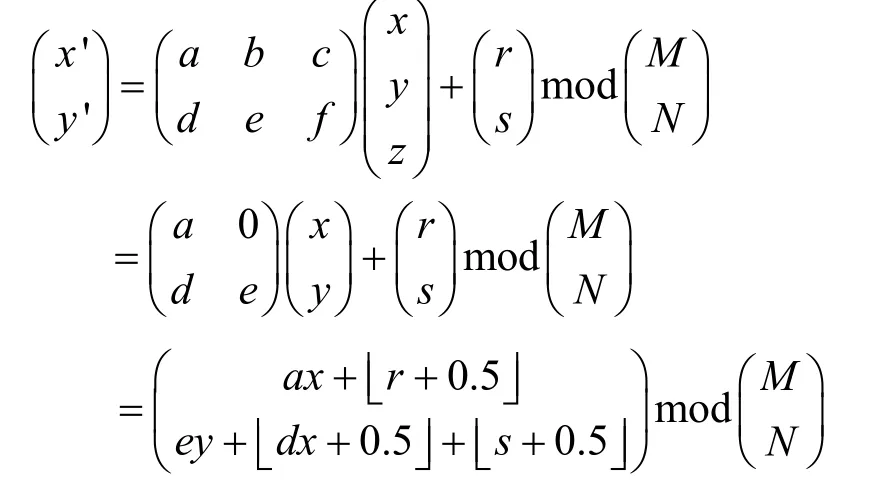
综上可知，置乱变换式（1）是(x, y, z)→(x', y', z')的一一映射。同理，置乱变换式（2）也是(x, y, z) → (x', y', z ')的一一映射。

三维类仿射置乱变换引入实数作为参数，与用整数作为参数相比，置乱的情况更加复杂。它在置乱像素位置的同时根据坐标混合像素值，可以加大图像的信息熵，均衡灰度直方图。较之于仅置乱像素位置的二维置乱变换，它相当于在MNL××的三维空间上进行置乱，具有更多大于0的Lyapunov指数，安全性更高。在实际中，可限制b (或d),,g h小数部分的二进制形式取00、01、或11， ,,r s t小数部分的二进制形式取0或1，使得置乱时乘积计算的复杂度相当于定点乘。

3 加密算法

采用上述置乱变换后，虽然像素位置和像素值被搅乱了，但像素之间没有任何计算关系，容易受到选择明文攻击，因此在三维类仿射变换的基础上引入扩散操作，并且根据加密过程中的数据扰动混沌系统，以进行自适应代换。如此进行三维类仿射置乱、扩散、代换和再扩散，迭代3轮后得到密文。算法综合使用了引言中提到的3种基本操作，充分发挥了扩散的作用，避免了文献[1～8]中算法设计的不足，并且吸纳了文献[8]中自适应加密的思想，使得在相同密钥情况下每一幅明文的等效密钥都不同，大大增强了算法的安全性。这种设计使得算法迭代1轮便可以把图像数据变成类似于随机噪声的形式，而且攻击者很难进行选择明文攻击。算法中迭代轮数越多，明密文之间的非线性关系越复杂，越难进行攻击。为进一步提高算法的安全性并使运算量不至于太大，设置迭代轮数为3轮。具体的加解密框架如图1所示。

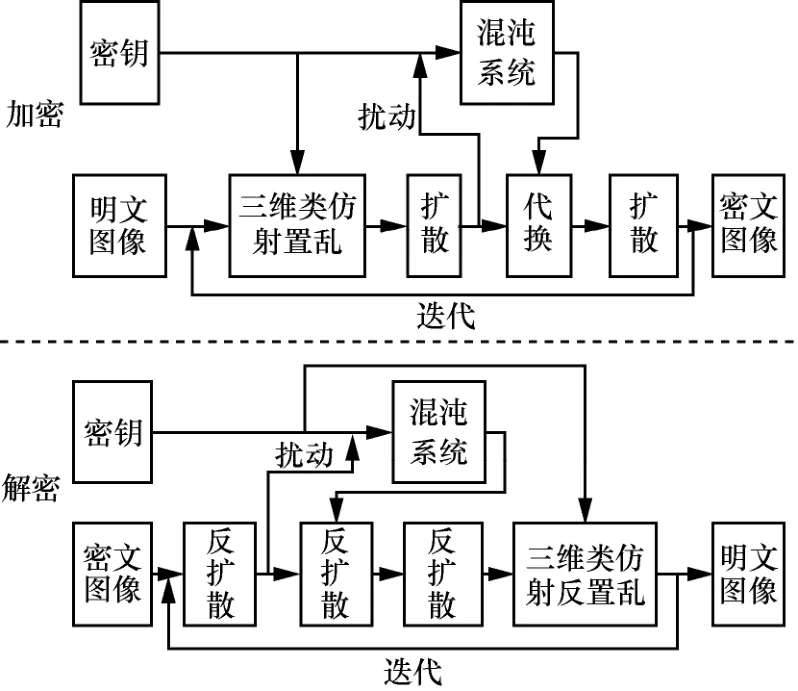
图1 加密解密框架

3.1 扩散

将图像(M行N列)中的像素按从左到右、从上到下的顺序，用逐个进行扩散， Pi代表第i个像素扩散之前的值， Ci代表扩散之后的值， i ∈[0,M N-1],⊕表示按位异或操作。当 i = 0 时，取 Ci-1= PMN-1。

3.2 混沌系统

混沌系统具有以下几个适用于加密的特性：1）对参数和初始条件极其敏感；2）输出有界，具有遍历性，类似于随机噪声；3）任意接近的 2点随着迭代的进行都会指数性发散。在实际中，一维混沌系统容易遭到相空间重构方法攻击，构造复合混沌系统可以解决这一问题。在文献[6]处理混沌系统的基础上，此处选用形式简单的三维Henon映射、Logistic映射、Tent映射、Cubic映射和Chebychev映射构造新的复合混沌系统。改写这 5种映射的形式并限制参数和初值的范围，分别记为混沌0、1、2、3、4，如图2所示。

图2 混沌系统

3.3 扰动混沌系统

在保证加密可逆的前提下，可用中间结果扰动混沌系统，使产生的混沌序列与图像数据密切相关，进一步增强抵御攻击的能力，如图3所示。

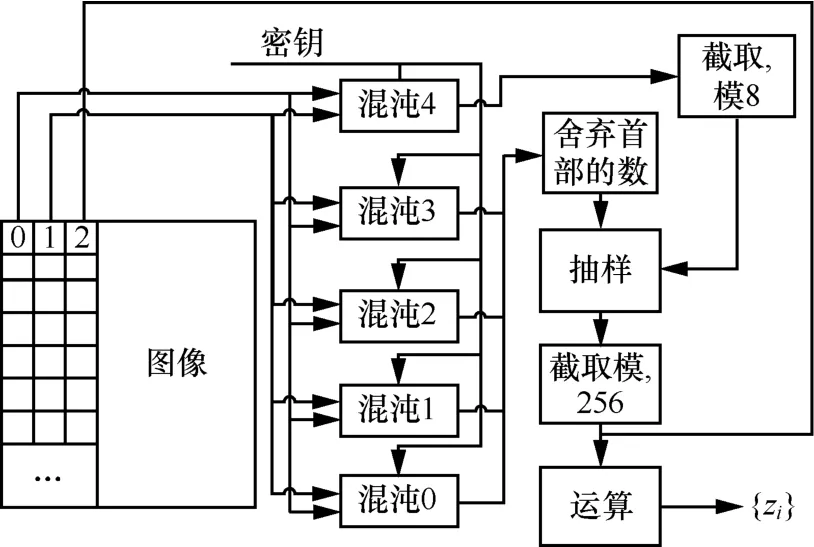
图3 扰动混沌系统

1) 设加密密钥为(k1k2,k3k4k5k6k7,k8k9, k10k11,k12k13, k14k15)，其中， k1代表三维类仿射变换的参数(a, b, c, d, e, f, g, h, l, r, s, t)， k2代表从混沌序列首部舍弃数值的个数，其余的子密钥分别代表混沌0、1、2、3、4的参数和初值。

2) 在对某一行像素进行代换之前，取该行前2个像素值 I0、 I1，调整子混沌系统的参数和初值，如图4所示。

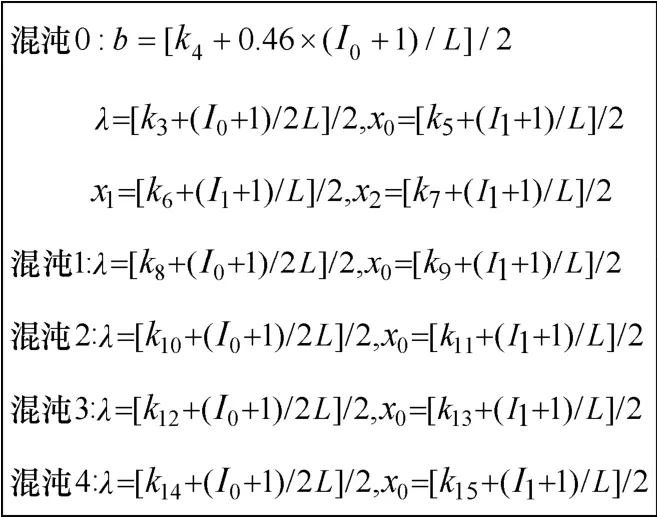
图4 调整参数和初值

3) 迭代混沌4得到十进制实数序列 { y '4,i}，取小数部分的第3位和第4位组成一个位于0 ～ 99之间的整数，模8映射为 { y4,i}。迭代混沌0、1、2、3，均舍弃前 k1个值，然后根据 { y4,i}对它们抽样，得到 { y '0,i}、{y'1,i}、{y'2,i}、{y '3,i}。提取这4个序列中每个实数的小数点后第2位到第4位组成一个整数，模256，对应映射为 { y0,i}、{y1,i}、{y2,i}、{ y3,i}。

4) 用该行第 3个像素值 I2控制混沌系统的耦合方式，计算产生{zi}，如图5所示。

3.4 代换

代换每一行像素时都用该行前3个像素重新扰动混沌系统，产生新的{zi} ，然后通过计算式对该行中前3个像素以外的所有像素进行计算，P 'i+3代表当前行第 i +3个像素代换之前的值， C 'i+3代表代换之后的值，i∈[0,N -4]。从上到下依次代换每一行。

图5 控制耦合方式

4 实验及算法评价

用VC++实现本文的加解密算法，按照图6设置密钥的初值，对1 024×1 024大小的256色图像man（如图7所示）加密，再解密，分别得到图8和图9。

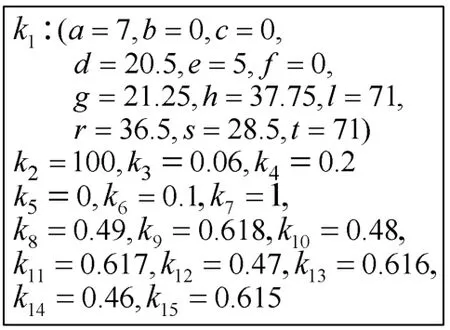
图6 密钥初值

图7 man

图8 man加密后

图9 正确密钥

4.1 加密视觉效果

数字图像加密要求密文与明文的视觉效果完全不同，目前可以从相邻像素相关性、明密文相似度、信息熵、峰值信噪比和自相关度这5个方面评判加密的视觉效果，相关的具体实验数据如图10～图18所示。

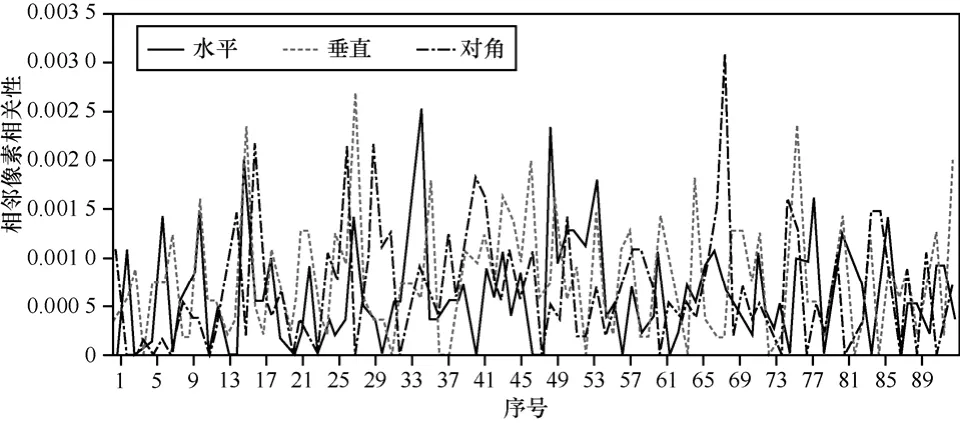
图10 相邻像素相关性

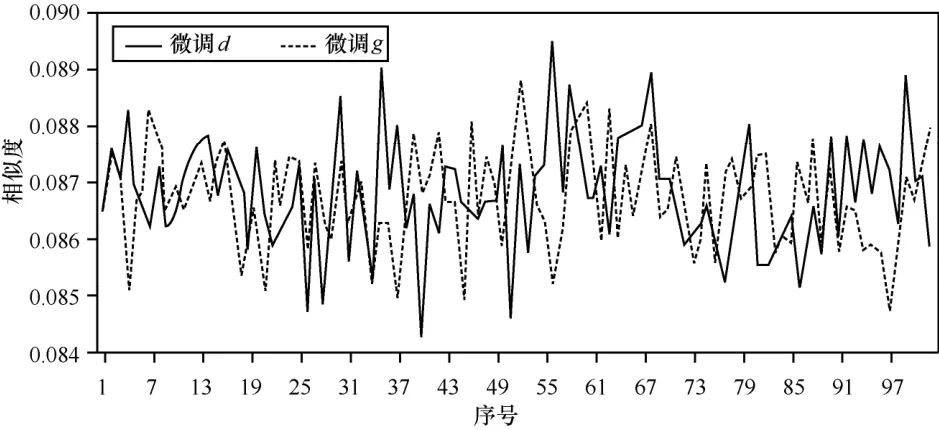
图11 相似度1

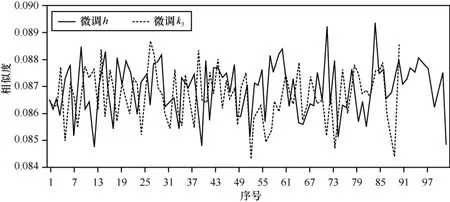
图12 相似度2

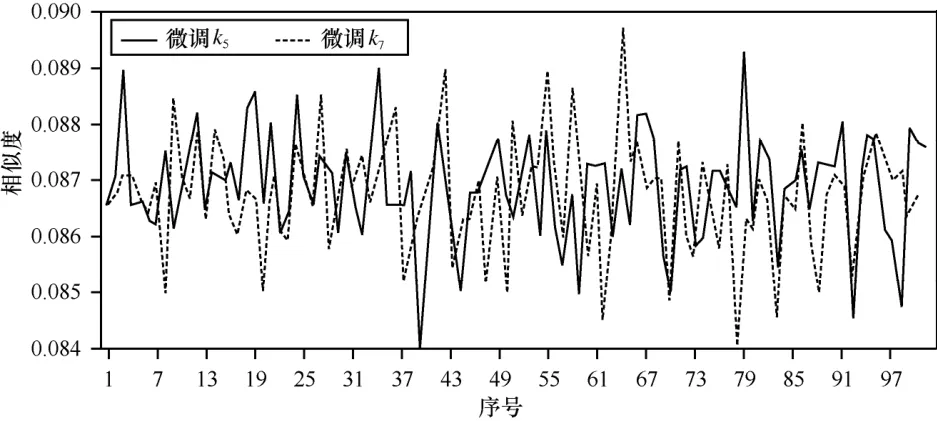
图13 相似度3

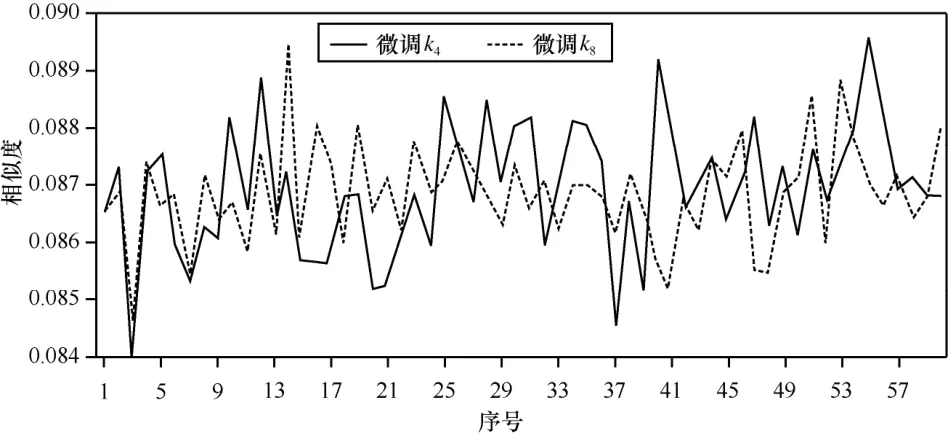
图14 相似度4

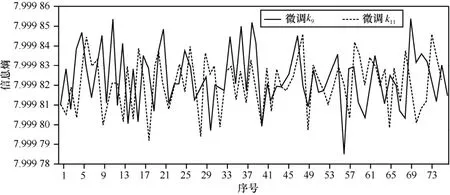
图15 信息熵1

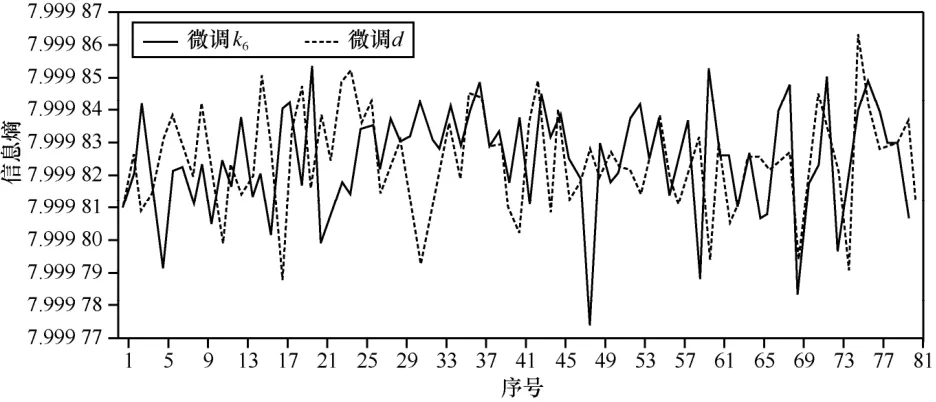
图16 信息熵2

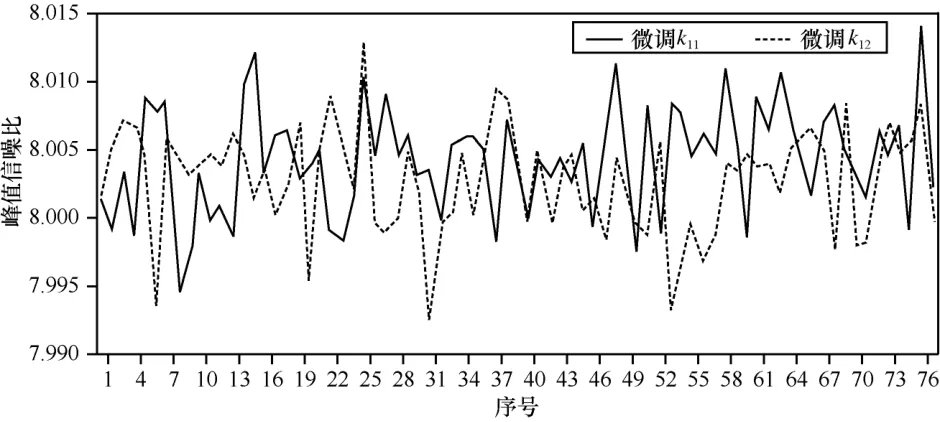
图17 峰值信噪比

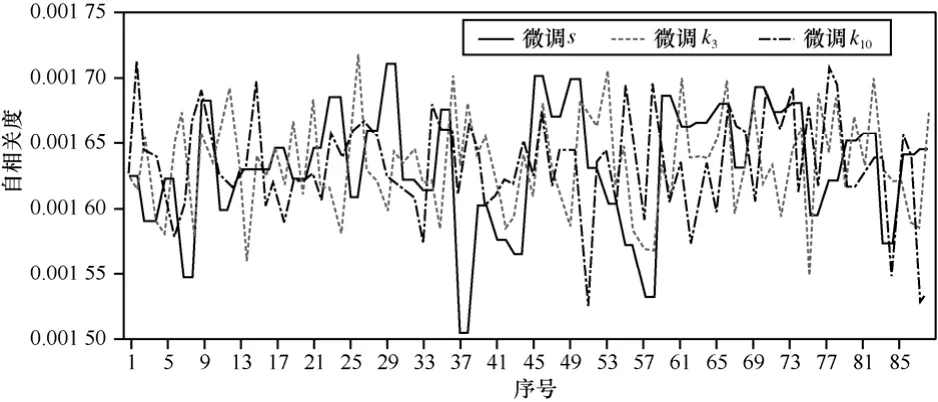
图18 自相关度

1) 相邻像素相关性

对于图像中的水平、垂直、对角相邻像素，相关性xyr通过下式计算：其中，xi、yi代表相邻的像素值。以上述密钥的取值为基数，不断微调14k，对man加密后相邻像素相关性如图10所示，微调其他参数略。图像man的水平相邻像素相关性为0.993 268，垂直为0.994 410，对角为0.990 168，加密后3个方向的相关性均小于0.003 5，密图无法辨认。

2) 明密文相似度

设明文图像为 P( M ×N)，密文图像为C( M ×N)，则两幅图像的相似度为XSD=1-2幅图像差别越大相似度越小，完全相同时相似度为 1。不断微调密钥中的参数d、g对man进行加密，计算得出的相似度如图11所示；微调h、3k，相似度如图12所示；微调5k、7k，相似度如图13所示；微调4k、8k，相似度如图14所示。可以看出，相似度均小于0.09，明密文差异显著。

3) 信息熵

设 vi表示L级灰度图象的第i个灰度值,p( vi)表示图像中具有第i个灰度值的像素所占的比例。图像的信息熵定义为：信息熵可以度量图像中灰度值的分布情况，灰度分布越均匀，信息熵越大，反之信息熵越小，它的最大值为 8。不断微调9k、11k对 man进行加密，计算得出的信息熵如图15所示；微调6k、d，信息熵如图16所示。图像man的信息熵为7.523 737，加密后信息熵均大于7.999 77，说明灰度分布很均匀，算法能有效地抵御统计攻击。

4) 峰值信噪比

5) 自相关度

设图像 P ( M ×N)是一灰度级为L的图像，(i, j)是其中的一个像素点， r, m均为整数，则点(i, j)的r- m 相关集为r和m分别称为像素间距和灰度差，0＜ r≤M/2，0≤m＜L。图像P的r-m自相关度定义为：表示集合中的元素个数。令r=1，m=60，不断微调s、 k3、 k10，对man加密后的自相关度如图18所示。图像man的自相关度为0.966 988，加密后自相关度均小于0.001 75，密文不可识别。

4.2 安全性分析

算法耦合了多个混沌系统，在每1轮迭代中都有1次三维类仿射置乱、2次非线性的扩散和1次自适应代换。其中的三维类仿射置乱采用了矩阵变换的形式，继承了二维非等长置乱变换的优点，能快速地打散并搅匀像素，具有混沌特性；它还继承了拟仿射变换的优点，没有不动点。实验证明，仅1次三维类仿射置乱便能使图像完全不可识别并且灰度直方图趋向于均衡化。在三维类仿射置乱的基础上，算法用图像中的像素值扰动敏感性强的混沌系统以进行自适应的代换，而且尽可能多地穿插使用了非线性的扩散操作，这种设计使得明密文对之间的映射关系非常复杂，具有很强的密钥敏感性和密文敏感性，符合密码学中的扩散与混淆原则。

1) 密钥空间

k1中的b(或者d),g, h, r, s, t均用8位二进制数表示，k1中的l用7位二进制数表示，k2用10位二进制数表示，k3、k4、k5、k6、k7、k8、k9、k10、k11、k12、k13、k14、k15这 13个参数均用15位二进制数表示，再加上 k1中的a与e，密钥长度大于8×6 + 7+10+13× 15=260bit，密钥空间巨大。DES算法密钥长度为56bit，3-DES为112bit或168bit，IDEA 为 128bit，AES 为 128bit、192bit或 256bit，文献[4]小于200bit。260bit已超过目前可接受的安全长度，假设攻击者以每秒搜索1 000万亿个密钥的速度穷举攻击，需要 3 .324 8× 1055年以上才能搜索完所有密钥，算法能够有效地抵御穷举攻击。

2) 密钥敏感性

令密钥中的参数 k8= k8+ 2-15，解密图8得到图19；令 k9= k9+ 2-15，解密得到图20；令 k13= k13+2-15，解密得到图 21；令 k15= k15+2-15，解密得到图 22，扰动其他参数略。可以看出，算法具有很强的密钥敏感性，密钥的微小改变都会导致解密失败。

图19 微扰k8

图20 微扰k9

图21 微扰k13

图22 微扰k15

3) 密文敏感性

攻击者可能对明文图像作微小改动并观察密文的变化，以发现明密文之间的某些关系。如果微小的改动导致密文很大的变化，那么这种差分攻击就会非常无力，可采用像素改变率NPCR 、平均变化强度UACI 来衡量这种敏感程度。设明文对应密文1C，将明文中某一个像素点的灰度值加1后再加密得到2C，则其中，当1(,)C i j时 (,)q i j=0，否则 (,)q i j=1。改动man中不同像素，计算出一系列NPCR 和UACI ，如图23和图24所示。可以看出NPCR ＞0.991 85，UACI ＞0.332 4，即明文中1个像素的微小改变将带来密文中99.185%以上像素的变化，变化幅度在 33.24%以上。密文敏感性强，算法有很强的抗差分攻击能力。

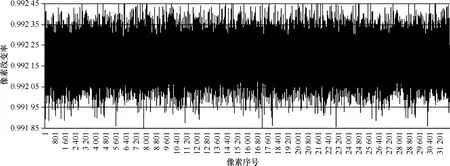
图23 像素改变率

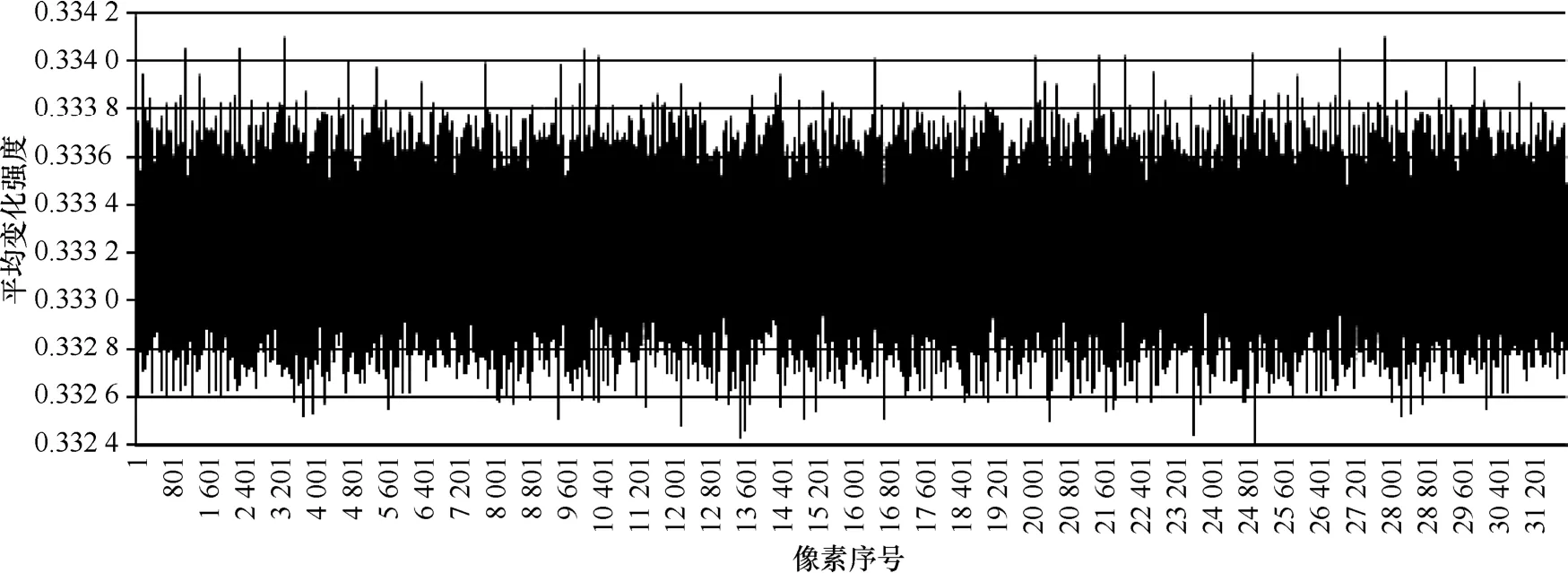
图24 平均变化强度

5 结束语

本文的加密算法首先采用三维类仿射变换打乱像素的位置并根据像素坐标混合像素值，然后依次进行非线性的扩散、代换、再扩散，在代换时根据图像当前数据扰动耦合的多个混沌系统，使产生的混沌序列与图像本身密切相关。其中的置乱操作可以直接作用于任意大小、任意宽高比的图像，不需要预处理；构造的混沌系统形式简单，符合模块化设计思想，易于并行实现，计算复杂度较小。算法加密视觉效果好，密图无法识别；密钥空间巨大，

可有效抵御穷举攻击；密钥敏感性和密文敏感性强，符合密码学中的扩散与混淆原则，可抵御选择明文攻击。进一步的研究内容是在算法中融入更高维的混沌系统，用于产生三维类仿射变换的参数，并且使置乱操作也受图像数据扰动。

[1] HUANG F, FENG Y. An image encryption approach based on a new two-dimensional map[A]. Proceedings of International Conference on Intelligent Information Hiding and Multimedia Signal Processing 2006[C]. CA, USA, 2006. 125-130.

[2] MENG J L, PANG H J, GAO W Q. New color image encryption algorithm based on chaotic sequences ranking[A]. Proceedings of International Conference on Intelligent Information Hiding and Multimedia Signal Processing 2008[C]. Harbin, China, 2008. 1348-1351.

[3] HANG H Y. A new image scrambling algorithm based on queue transformation[A]. Proceedings of the Sixth International Conference on Machine Learning and Cybernetics 2007[C]. Hong Kong, China,2007. 1526-1530.

[4] SHANG Z W, REN H E, ZHANG J. A block location scrambling algorithm of digital image based on arnold transformation[A]. Proceedings of the 9th International Conference for Young Computer Scientists 2008[C]. Hunan, China, 2008. 2942-2947.

[5] BIBHUDENDRA A, SARAT K P, GANAPATI P. Image encryption by novel cryptosystem using matrix transformation[A]. Proceedings of First International Conference on Emerging Trends in Engineering and Technology 2008[C]. Nagpur, Maharashtra, 2008. 77-81.

[6] 王培荣,徐喆,付冲等.复合混沌数字图像加密算法[J].通信学报,2006,27(11A):285-289.WANG P R, XU Z, FU C, et al. Composed chaos-based image encryptionalgorithm[J]. Joumal on Communications, 2006, 27(11A): 285-289.

[7] WANG F C, BAI S, ZHU G B, et al. An image encryption algorithm based on N-Dimension affine transformation[A]. Proceedings of the Eighth IEEE/ACIS International Conference on Computer and Information Science 2009[C]. Shanghai, China, 2009. 579-585.

[8] CHEN G, ZHAO X Y, LI J L. A self-adaptive algorithm on image encryption[J]. Journal of Software, 2005, 16(11):1975-1982.

[9] CHEDDAD A, CONDELL J, CURRAN K, et al. A Hash-based image encryption algorithm[J]. Opt Commun, 2010, 283:879-893.

[10] 郭建胜,金晨辉.对基于广义猫映射的一个图像加密系统的已知图像攻击[J]. 通信学报, 2005, 26(2):131-135.GUO J S, JIN C H. An attack with known image to an image cryptosystem based on general cat map[J]. Journal on Communications, 2005,26(2):131-135.

[11] TAO R, MENG X Y, WANG Y. Image encryption with multiorders of fractional Fourier transforms[J]. IEEE Transactions on Information forensics and Security, 2010, 5(4):734-738.

[12] LI X X, ZHAO D M. Optical color image encryption with refined fractional Hartley transform[J]. Optik, 2010, 121(7):673-677.

[13] ZHOU N R, DONG T J, WU J H. Novel image encryption algorithm based on multiple-parameter discrete fractional random transform[J].Optics Communications, 2010, 283(11):3037-3042.