四维余代数的分类

2017-02-07范中平

浙江大学学报（理学版） 2017年1期

关键词：同构等价代数

范中平

(中国海洋大学数学科学学院，山东青岛 266100)

四维余代数的分类

范中平

(中国海洋大学数学科学学院，山东青岛 266100)

利用余代数的树结构基，得到了余代数同构的等价条件，从而完成了四维余代数的分类，并针对更高维的余代数分类给出了一般方法.

余代数；余根滤链；树结构基

The classification of 4-dimensional coalgebra. Journal of Zhejiang University(Science Edition), 2017,44(1):028-032

0 引言

余代数结构的研究是含幺结合代数、双代数和Hopf代数相关研究中的重要部分，受文献[1-3]中非点态非余半单的Hopf代数分类方法的启发，通过余代数的余根滤链分层考虑余代数的结构.余根滤链中上层元素的余结构要涉及下层元素需满足某些特定条件；反之，给定了余根滤链中的下层下元，可以按这些特定条件穷举可能的余根滤链中的上层元素，进而给出整个余代数的余结构.则称这种上下紧密关联的结构为树结构.通过这种树结构给出的基称为树结构基.

本文定义了树结构的等价关系，使得树结构基的等价类与余代数的同构类一一对应.通过穷举树结构基的等价类完成四维余代数的分类，这种分类方法对更高维的余代数具有通性.由于有限维情形下，余代数与含幺结合代数互为对偶，则相同维数的含幺结合代数的分类亦可借助此方法.

假设k是一个特征为零的代数闭域.在下文的讨论中，如不另作说明，线性空间在k上都是有限维的.

1 余代数的树结构基

本节定义余代数的树结构基.

对于余代数(C,Δ,ε)，由文献[4] Theorem 5.4.2给出的余根分解知，存在一个余理想I和一个C到其余根C0的满同态π:C→C0,使得C=C0⨁I和ker π=I.固定此余理想I，并定义

ρL=(π⊗id)Δ和ρR=(id⊗π)Δ.

(1)

容易验证，(C,ρL,ρR)为一个C0-双余模.

定义一组C的子空间Pn,n≥0如下：

P0=0,

P1={c∈C|Δ(c)=ρL(c)+ρR(c)}= Δ-1(C0⊗I+I⊗C0),

Pn={c∈C|Δ(c)-ρL(c)-ρR(c)∈

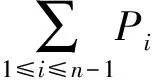
记C的余根滤链为{Cn}n≥0.由文献[1] Lemma 1.1知，Pn=Cn∩I.

则有

命题1(文献[3]Lemma 3.1) 如果对c∈Pn,n≥2,有c∉Pn-1，那么对所有的n′∈{1,2,…,n-1}，有

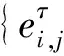
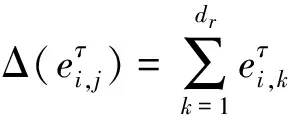
对一个余代数的单左余模，其对偶空间为此余代数的单右余模.且一个单余代数有唯一的单左余模和唯一的单右余模同构类，所以对τ∈，可以固定Vτ和分别作为Dτ-单左余模和Dτ-单右余模同构类的代表元.则有

(2)

任意的C0-双余模可以分解成其C0-单双余子模的直和.对任意的C0-单双余模M，存在τ,μ∈，使得作为C0-双余模,有

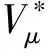
(3)

容易验证，对n≥1,有Pn关于ρL,ρR是C的C0-双余子模，则Pn可以分解成C0-单双余子模的直和.对τ,μ∈,记为Pn同构于Vτ⊗的C0-单双余子模的和，有

注意到Pn-1⊆Pn是一个C0-双余子模，那么存在一个Pn的C0-双余子模Qn，使得

Pn=Pn-1⨁Qn.

注意Qn的选取不是唯一的.

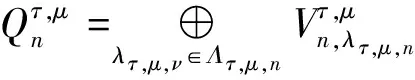
C=C0⨁I=C0⨁∪n≥1Pn=C0⨁⨁n≥1Qn=

⨁σ∈Dσ⨁

⨁σ∈Dσ⨁).

由式(2)知，有C0-双余模同构：

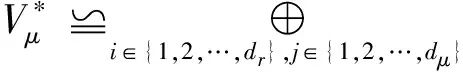
(5)

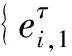
ρL(ωi,j)=(id⊗f-1)(Δ⊗id)f(ωi,j)=

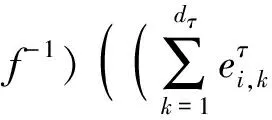
(6)

和

ρR(ωi,j)=(f-1⊗id)(id⊗Δ)f(ωi,j)=

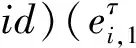
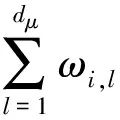
(7)

并且由Pn的定义知

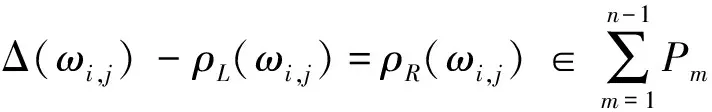
(8)

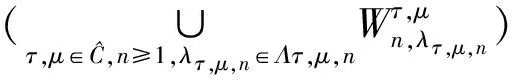
(9)

由式(4)知，WC是余代数C的一组基.

定义1 对余代数C,继承前面讨论中的记号，称WC为C的一个由W0和I构造的树结构基.

2 树结构基的等价类

本节给出树结构基的等价关系，使得研究余代数的同构类与此等价关系下树结构基的等价类一一对应.

令W为由W0和I构造的余代数C.树结构基W的余结构指双线性集合FW={Fω:kW×kW→k|ω∈W},这里kW是以W为基生成的线性空间.其中的双线性型由下式定义：对任意的ω0∈W,

对余代数C和D，称C的树结构基WC与D的树结构基WD有一致的余结构，如果存在线性映射θ:C→D,使得θ(WC)=WD且对ω∈W，有

ΔDθ(ω)=(θ⊗θ)ΔC(ω).

显然θ是C到D的余代数同构，且对任意的ω0,ω1,ω2∈WC,Fω0∈FWC,Fθ(ω0)∈FWD，有

Fω0(ω1,ω2)=Fθ(ωυ)(θ(ω1),θ(ω2)).

接下来分三方面讨论树结构基之间的联系.

(a)首先给出一个余代数在同一余根分解下的不同树结构基之间的联系.

仅改变C的单余子代数标准基的选取不会影响C的C0-双余模结构，所以与I和不同单余子代数标准基构造的树结构基相差一个线性双射.以下讨论中都不改变C的单余子代数标准基的选取，所以与I和不同的单余子代数标准基构造的树结构基之间有一致的余结构.

假设W′为由W0和I构造的但不同于W的C的树结构基.

(10)

(b)然后给出一个余代数在不同余根分解下的树结构基之间的关系.

假设存在余代数满同态π1:C→C0和余理想I′⊂C，使得C=C0⨁I′,kerπ1=I′.则存在自然的投射π2:C→I′，使得对任意的x∈C，有

c=π1(c)+π2(c).

(11)

定义一个线性映射φ:C→C如下：

对ω∈W,

(12)

容易验证，φ是双射，且φ(W)是C的一组基.

命题2 对余代数(C,Δ,ε)，由式(12)定义的φ是C的余代数自同构.

证明由φ|C0=id知，证明此命题等价于证明对任意的ω∈WW0，有

Δ(φ(ω))=(φ⊗φ)Δ(ω).

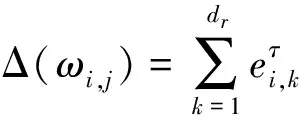
这里kωi,j,ω1,ω2∈k，且只有有限个非零.则有

Δ(φ(ωi,j))=Δ(ωi,j-π1(ωi,j))=

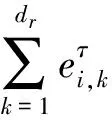
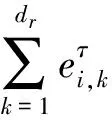
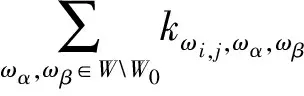
显然，上式中第1项属于I′⊗C0,第2项属于I′⊗I′，第3项属于I′⊗I′,而最后1项属于C0⊗C0.由I′为余理想知，Δ(φ(ωi,j))⊂I′⊗I′+I′⊗C0+C0⊗I′.则最后一项为0.

所以有

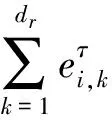
命题得证.

由命题2,有φ(W)是一个由W0和I′构造的C的树结构基，且W与φ(W)的余结构一致.

(c)最后考虑同构的余代数间的树结构基的关系.

假设f:C→D为一余代数同构.显然有f(C0)=D0,f(I)为D的一个余理想，且D=D0⊗f(I).

容易验证，f(W)是一个由f(W0)和f(I)构造的D的树结构基.且由f为余代数同构知，W和f(W)有一致的余结构.

下面给出树结构基的等价类的概念，并将其与余代数的同构类联系起来.

定义2 对任意的W1,W2∈Ωm，假设W1为余代数C的树结构基，W2为余代数D的树结构基,如果存在一个线性双射φC:C→C,使得φC(W1)是C的树结构基，且φC(W1)与W2有一致的余结构，称W1与W2是等价的.

注2 此等价关系的定义良好；自反性与传递性显然.要说明对称性，即说明如果W1与W2是等价的，那么存在一个线性双射φD:D→D，使得φD(W2)是D的树结构基，且φD(W2)与W1有一致的余结构.

显然由φC(W1)与W2有一致的余结构知，C与D之间存在余代数同构θ.由(c)知，θ(W1)是D的树结构基且与W1有一致的余结构.由(a)知，存在线性双射φ′:D→D,使得φ′(W2)=θ(W1).令φD=φ′，则φD(W2)是D的树结构基，且φD(W2)与W1有一致的余结构.

综合(a),(b)和(c)，显然同一余代数的树结构基是等价的，且有

定理1 余代数C和D是同构的等价于对任意的WC∈ΩC和WD∈ΩD，有WC等价于WD.

由此，分类m维的余代数就等价于给出Ωm的所有等价类，且穷举Ωm的等价类分为以下几步：

步骤1 确定W0的余结构；

步骤2 对n≥1，确定|Wn|；

步骤3 从n=1开始依次确定Wn的余结构，这里分成2步：对ω∈Wn,

步骤3a 确定ρL(ω)和ρR(ω)；

步骤4 验证由以上几步给出的W=W0∪∪n≥1Wn的余结构，使得以W为基生成的线性空间kW成为余代数；如成立，则W是kW的一组树结构基.

3 四维余代数的分类

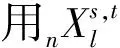
(13)

对于四维余代数，共有16个树结构基的等价类.

A 类群元有4个的情形：

第1类 W0={g0,g1,g2,g3}，则W=W0.

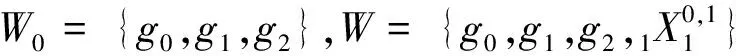
C 类群元有2个，|W1|=2的情形：

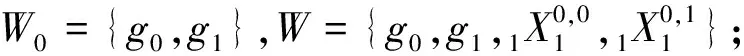
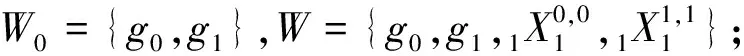
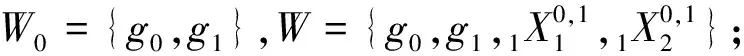
(0,0,0,0)～(1,1,1,1)；

(0,0,0,1)～(0,1,0,0)～(1,1,1,0)～(1,0,1,1);

(0,0,1,0)～(1,0,0,0)～(1,1,0,1)～(0,1,1,1);

(0,0,1,1)～(1,1,0,0);

(0,1,0,1)～(1,0,1,0);

(0,1,1,0)～(1,0,0,1).

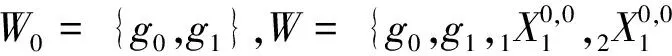
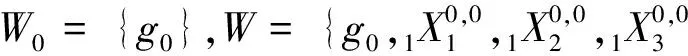
F 类群元有1个，|W1|=2，|W2|=1的情形：

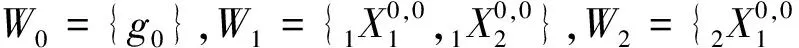
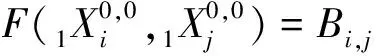
(14)

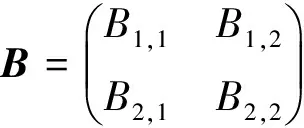
当P1的基固定时，P1×P1到k的双线性型与其度量矩阵一一对应，即

进行穷举过程的步骤5.令φ为任一满足步骤5要求的线性变换.记

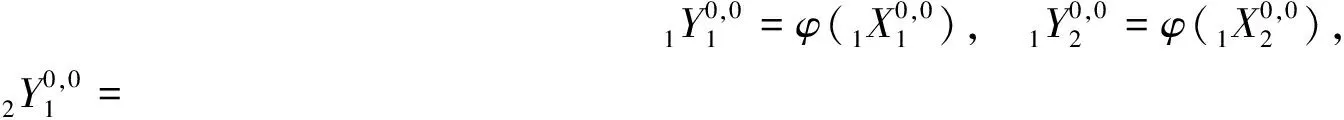
W′=φ(W).

记φ的基变换矩阵为Pφ,有Pφ∈GL2(k)且

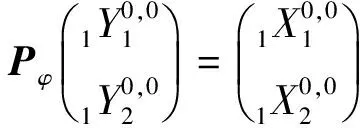
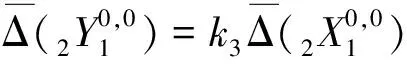
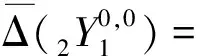
所以有

(15)

即矩阵B与B′是合同等价的.反过来每个合同变换的P矩阵都对应一个步骤5中的线性变换.所以，四维矩阵全体M2(k)的合同等价类与四维余代数的类群元有1个，|W1|=2,|W2|=1的情形的树结构基的等价类一一对应.

M2(k)的合同等价类如下：

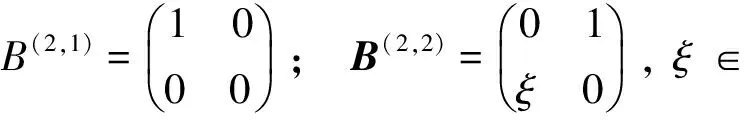
G 类群元有1个，|W1|=1,|W2|=2的情形：

H 类群元有1个，|W1|=1,|W2|=1,|W3|=1的情形：

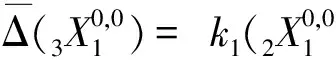
I 没有类群元的情形：

第16类 W0={ei,j}i,j=1,2,这里{ei,j}i,j=1,2为一个四维单余代数的标准基.

综上所述，有定理2 所有k上的四维余代数同构类如下，这里省略了自明的余结构：

(1)C[4.1]=k{g0,g1,g2,g3}.

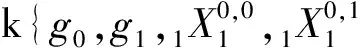
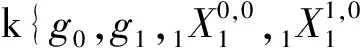
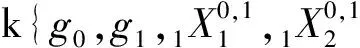
(16)C[4.16]=M*(2,k),这里M(2,k)表示一个k上的四维矩阵代数.

[1] ANDRUSKIEWITSCH N, NATALE S. Counting arguments for Hopf algebras of low dimension[J]. Tsukuba Journal of Mathematics, 2001,25(1):187-201.

[2] BEATTIE M, DSCLESCU S. Hopf algebras of dimension 14[J]. Journal of the London Mathematical Society,2004,69(1):65-78.

[3] FUKUDA D. Structure of coradical filtration and its application to Hopf algebras of dimensionpq[J]. Glasgow Mathematical Journal, 2008,50(2):183-190.

[4] MONTGOMERY S. Hopf Algebras and Their Actions on Rings[M]. Providence:American Mathematical Society, 1993.

FAN Zhongping

(SchoolofMathematicalSciences,OceanUniversityofChina,Qingdao266100,ShandongProvince,China)

By employing the tree structure basis of coalgebra, an equivalent condition for coalgebra being isomorphic is achieved. The list of all isomorphism classes of 4-dimensional coalgebra is completed, and a general method for the classification of larger dimensional coalgebra is provided.

coalgebra; coradical filtrations; tree structure basis