基于OFDM协作中继的机会主义频谱共享协议及其最优资源分配

卢为党，吴宣利，沙学军，张乃通

（1. 浙江工业大学 信息工程学院，浙江 杭州 310023；2. 哈尔滨工业大学 通信技术研究所，黑龙江 哈尔滨 150080）

1 引言

随着无线通信服务的爆发式发展，无线电频谱资源变得越来越紧张。而在现有的频谱授权机制中，为了使各个系统之间不产生干扰，每个系统都独自占有一段频谱，没有授权的系统不允许接入这些频谱。这种固定的频谱分配方式使得频谱利用率很低，造成了频谱资源的大量浪费。美国联邦通信委员会（FCC, federal communications commission)的研究报告中指出现有的授权频谱的利用率只有15%～85%[1]。认知无线电技术具有在不影响授权用户即主用户性能的前提下允许非授权用户即认知用户接入授权用户的频谱，可以有效地提高频谱资源的利用率[2～4]。国内外已有不少文献对认知无线电中的频谱接入技术进行了研究[5～7]。当认知用户发现主用户中有频谱空洞时，认知用户就可以接入这段空闲的频谱[5]。之后又有学者提出,只要认知用户对主用户造成的干扰小于一定的门限时，认知用户就可以共享主用户正在使用的频谱[6,7]。

最近，协作中继技术在认知无线电频谱接入中得到了广泛应用[8～11]。Simeone等研究了集中式的协作频谱租赁协议，在该协议中，主用户租赁自己的一部分发送时间给认知用户，而认知用户则利用一部分获得的发送时间帮助主用户中继信息作为回报[9]。在文献[10]和文献[11]中提出了一种基于协作中继的分布式频谱共享协议，认知用户接入主用户的频谱后，在协作的第2个阶段利用自己的一部分功率中继主用户信息帮助其达到要求的速率，利用剩余的功率来发送自己的信息。但是在文献[10]和文献[11]中，认知用户在第 2阶段同时发送主用户和自己的信息，在主用户和认知用户的接收端都会造成干扰，没有最优地利用资源。

针对以上问题，本文提出了一种基于 OFDM（orthogonal frequency division multiplexing）协作中继的机会主义频谱共享协议。在该协议中，当主用户的信道不好，不能达到要求速率时，如果认知用户能够协作帮助主用户达到其要求速率，则该认知用户就可以以协作的方式接入主用户的频谱。在该接入方式中，认知用户利用接入获得的一部分子载波中继主用户的信息，帮助其达到要求的速率，而利用剩余的子载波发送自己的信息。由于认知用户利用不同的正交子载波分别发送主用户和自己的信息，所以在主用户和认知用户的接收端均不会产生干扰。本文提出了在保证主用户达到要求速率的前提下，以最大化认知用户速率为目标的最优子载波分配和配对算法以及子载波上的功率分配算法。如果认知用户不能够协作帮助主用户达到其要求速率，为了有效地利用频谱资源，主用户停止发送信息，认知用户以非协作的方式接入主用户的频谱，利用接入的全部频谱来发送自己的信息。

2 系统模型及协议描述

2.1 系统模型

如图1所示，在一个基于OFDM的认知无线电系统中，主系统由一个主用户发送端(PT, primary transmitter)和主接收端(PR, primary receiver)组成，该系统是一个延迟受限的系统。主系统支持中继功能，有一段K个子载波组成的授权频谱。认知系统由一个认知用户发送端（CT, cognitive transmitter）和认知接收端（CR, cognitive receiver）组成。该系统只有在主用户达不到要求速率时才有机会接入主系统的频谱进行工作。假设认知系统能够模拟主系统中的无线电协议和系统参数。同时假设主系统和认知系统都经历独立的频率选择性衰落。

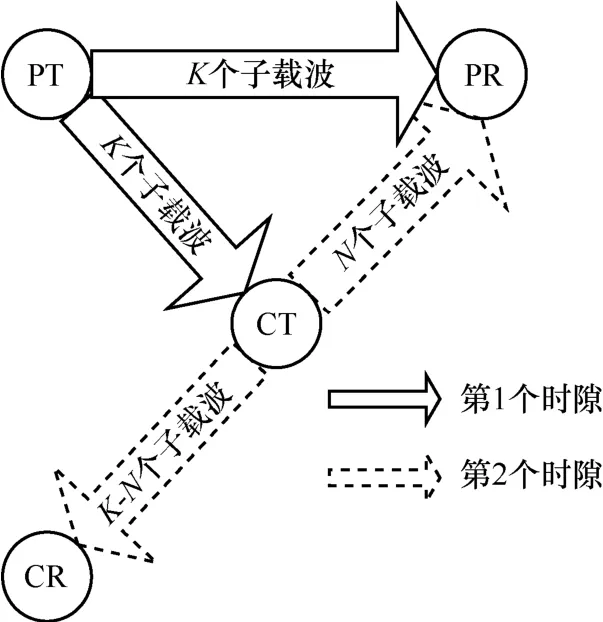
图1 系统模型

2.2 协议描述

1) 当没有认知用户接入时，主用户通过直传发送自己的信息，主用户的速率可以表示为

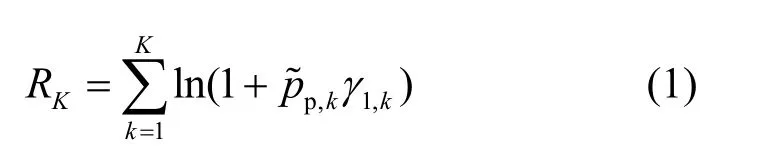
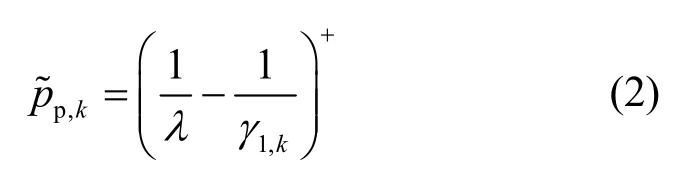
2) 当PR收到RTC后，PR就可以对PT-PR的信道进行估计，然后向周围用户广播应答协作信息(acknowledge-to-cooperate) ATC，其中，ATC中包含了PT-PR的信道信息。

3) 当 CT收到 RTC和 ATC后，CT可以对PT-CT和CT-PR的信道进行估计，并且能够获得主用户的要求速率 RT、功率 Pp和PT-PR的信道信息。得到这些信息后，CT就可以通过计算 Rmax来判断自己是否能够帮助主用户达到其要求速率 RT。其中， Rmax为CT完全作为PT中继时主用户所能获得的最大即时速率，即CT把自己所有的子载波和功率都用来帮助主用户中继时主用户所能达到的速率，在 3.2节中对 Rmax进行详细描述。如果Rmax≥RT，则CT向周围用户广播同意协作信息CTC (confirm-to-cooperate)，表示认知用户能够帮助主用达到其要求速率，认知用户以协作的方式接入主用户的频谱。其中，CTC中包含了认知用户的功率 Ps、PT-CT和CT-PR的信道信息。收到CTC后，主用户切换到协作模式。如果认知用户不能帮助主用达到其要求速率，为了有效地利用频谱资源，主用户停止发送信息，认知用户以非协作的方式接入主用户的频谱，利用接入的全部频谱来发送自己的信息。

3 认知用户接入频谱后主用户和认知用户可获得的速率

在协作接入方式下，信息的发送过程分为2个时隙。在第1个时隙，如图1中的实线箭头所示，PT用全部的K个子载波发送信息给PR和CT。PR和CT在第1个时隙子载波k上接收到的信息可以分别表示为

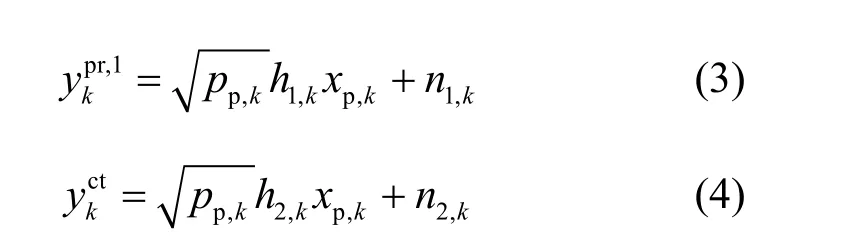
其中， xp,k表示主用户子载波k上的信息， h2,k表示PT在子载波k到CT的信道增益，n1,k和 n2,k分别表示PR和CT在子载波k上的加性高斯白噪声。这里的 pp,k是协作模式下PT在子载波k上的功率分配，和式(2)中的相比，直传时的功率分配不同。这里分别用Ωp和Ωs分别表示主用户和认知用户上的子载波集合， Ωp= {1,2,3,… ,K }，Ωs= {1,2,3,… ,K }。

在第2个时隙中，如图1中的虚线箭头所示，PT停止发送信息，CT用一部分接入获得的子载波帮助把 PT的信息中继转发给 PR。具体来说，CT利用子载波 k '( k '∈Gs)和在第1个时隙中收到的在载波k ( k ∈Gp)进行配对，然后放大转发给PR，其中，| Gp|=| Gs|=N 。假设 Gp中的一个子载波最多只能被 Gs中的一个子载波中继，而且 Gs中的一个子载波最多只能中继 Gp中的一个子载波。所以PR在第2个时隙接收到的信息可以表示为

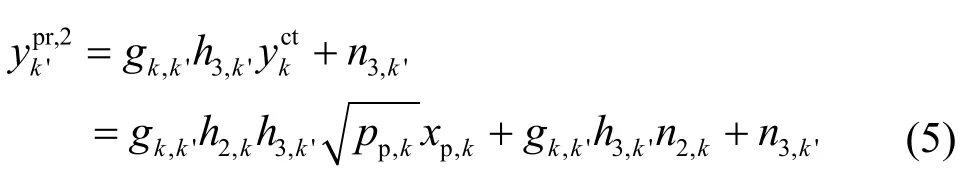
其中， h3,k'表示CT在子载波 k '到PR的信道增益，n3,k'表示 PR在子载波 k '上的加性高斯白噪声，为功率归一化参数，sp,'kp 表示在CT分配给用于协作的子载波 'k的功率。

PR通过2个时隙收到的信息可以表示为

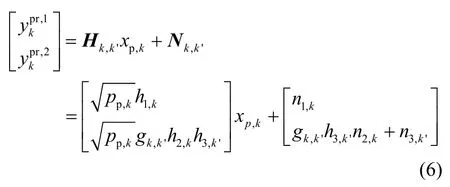
通过最大比合并，主用户在子载波k上通过CT子载波 'k中继帮助获得的速率可以表示为

3.1 协作接入方式下主用户和认知用户可获得的速率

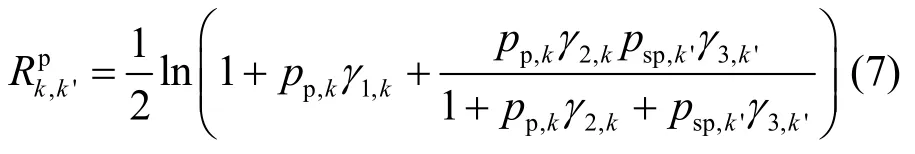
这里用 ρk,k'∈ { 0,1}表示子载波配对，如果在第1个时隙PT的子载波k和第2个时隙CT的子载波k'配对，则 ρk,k'= 1 。否则 ρk,k'= 0 。

所以主用户经过2个时隙后在所有子载波上可获得的速率可以表示为

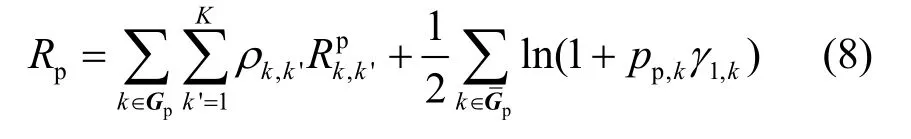
在第2个时隙中，CT同时利用剩余的子载波发送自己的信息，则认知用户可获得速率可以表示为

3.2 协作接入方式下主用户可获得的最大速率

当认知用户完全作为主用户的中继时，即把所有的子载波和功率都用来帮助中继主用户信息，Gp=Ωp，Gs=Ωs，主用户获得最大速率Rmax。此时主用户的速率可以表示为

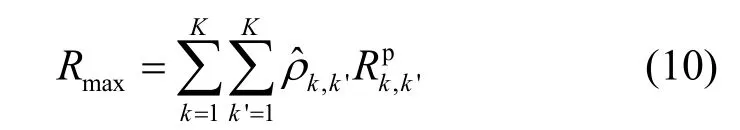
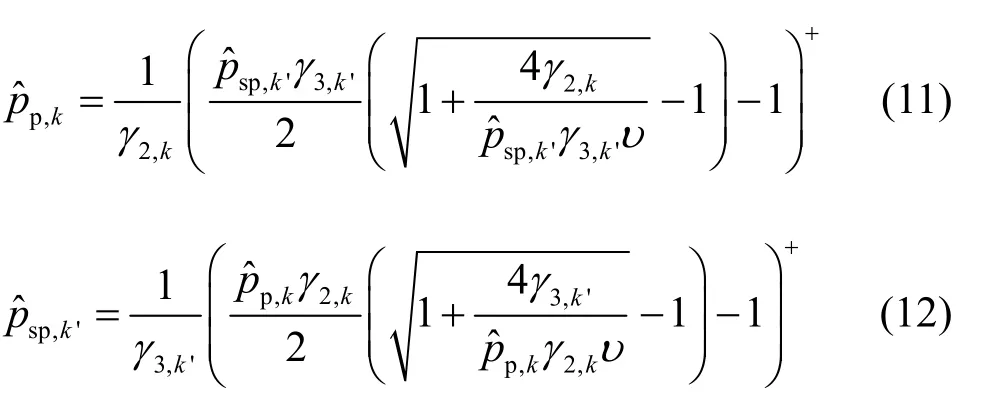
3.3 非协作接入方式下认知用户可获得的速率

在该方式下，认知用户不能帮助主用达到其要求速率，为了有效地利用频谱资源，主用户停止发送信息，认知用户以非协作的方式接入主用户的频谱，利用接入的全部频谱来发送自己的信息。认知用户可获得速率可以表示为

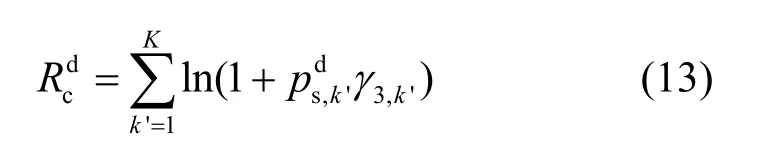
4 协作接入方式下最优资源分配算法

4.1 协作接入方式下的资源优化

这里研究在协作接入方式下，在保证主用户达到要求速率，认知用户的速率最大化为原则的最优资源分配，包括分配给主用户用于协作的最优子载波集合 Gp，最优子载波配对 ρ = {ρk,k'}和子载波功率分配 p ={ pp,k, psp,k', pss,k'}，即

满足以下条件：

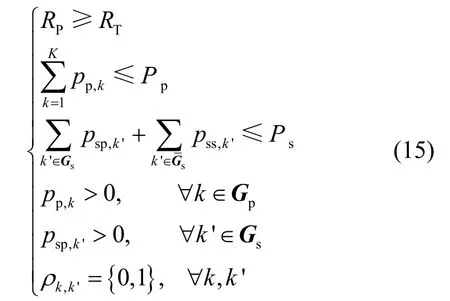
上述优化问题是一个NP问题，可以通过穷举方法求解，但是复杂度很高。而且由于主用户速率要求 RP≥RT的限制，使得该问题不是一个凸优化的问题。W. Yu等在文献[15]中证明，对偶算法可以用来等价求解上面这个非凸优化问题，只要该问题满足分时条件且子载波数足够多。很明显本文的问题满足分时条件，所以可以用对偶算法来求解式(14)中的问题。将上述这个问题分为2个步骤，首先优化对偶函数中的对偶变量，然后再对问题中的资源分配进行优化。

4.2 对偶变量优化

获得式(14)中的拉格朗日对偶函数为

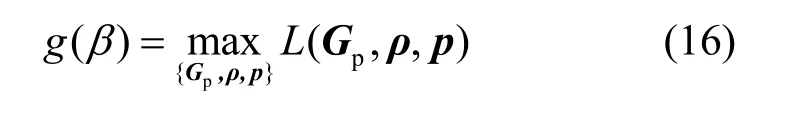
其中，拉格朗日算子 L ( Gp,ρ, p)为

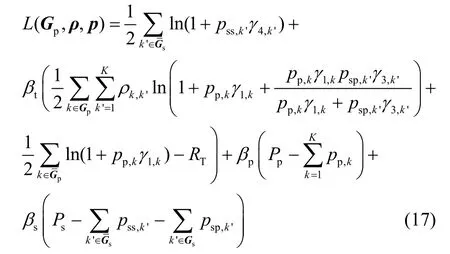
满足条件

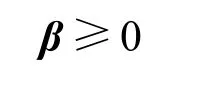
由于对偶函数是个凸函数[16,17]，所以可以利用次梯度法求解对偶变量。

g(β)的次梯度可以表示为

令 Δβ=(Δ βt, Δ βp, Δ βs)， β 通过 βt+1= βt+ξtΔβ来更新，其中，ξt为更新的步长大小。通过次梯度法可以获得收敛的最优对偶变量β。

4.3 资源分配优化

获得最优对偶变量β后，可以通过3个步骤分别得到分配给主用户用于协作的最优子载波集合Gp，最优子载波配对 ρ = {ρk,k'}和子载波功率分配p={ pp,k,psp,k', pss,k'}。首先对于给定的 Gp和ρ，可以获得最优p；然后对于给定的 Gp可以获取最优ρ；最后得到最优 Gp。

1) 给定 Gp和ρ，获得最优p：假设给定 Gp和ρ，式(17)可以变为

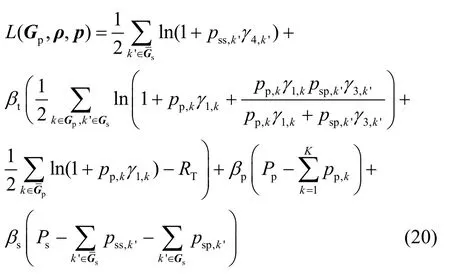
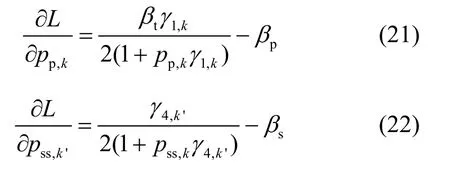
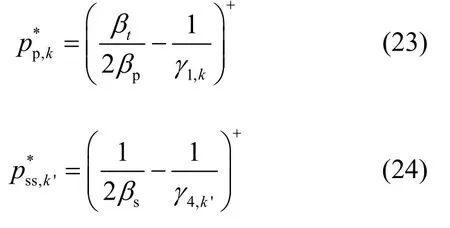
然后对PT中的子载波 k ∈Gp和CT中的子载波k'∈Gs进行功率优化，这部分子载波被用于协作传送主用户的信息。把式(20)分别对 pp,k,k∈Gp和psp,k', k'∈Gs求偏导，可以得到

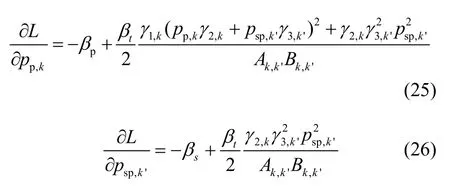
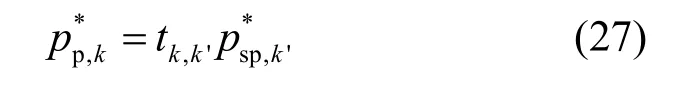
其中，

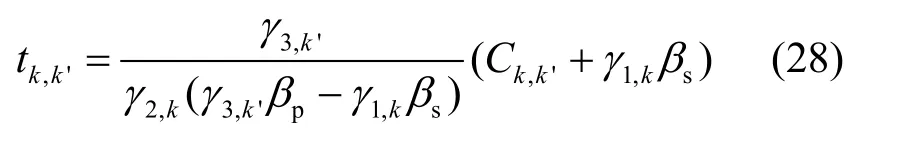
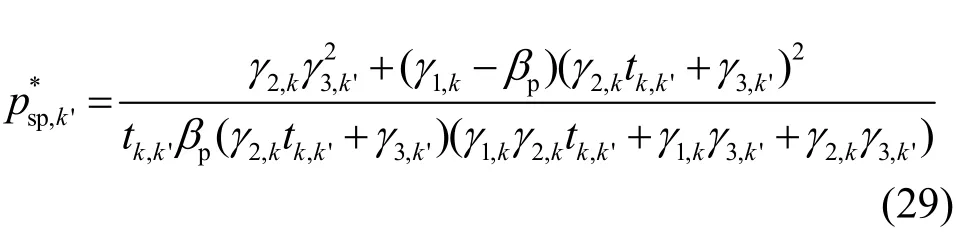
2) 给定 Gp，获取最优ρ：把式(23)、式(24)和式(27)、式(29)代入式(17)后，式(17)可变为

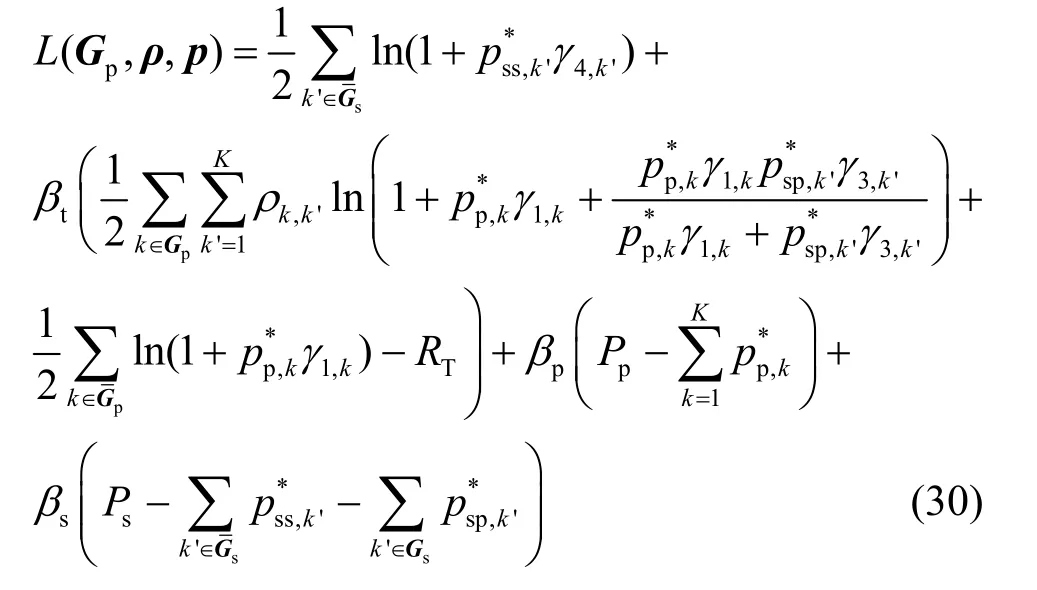
通过数学变换，可以得到

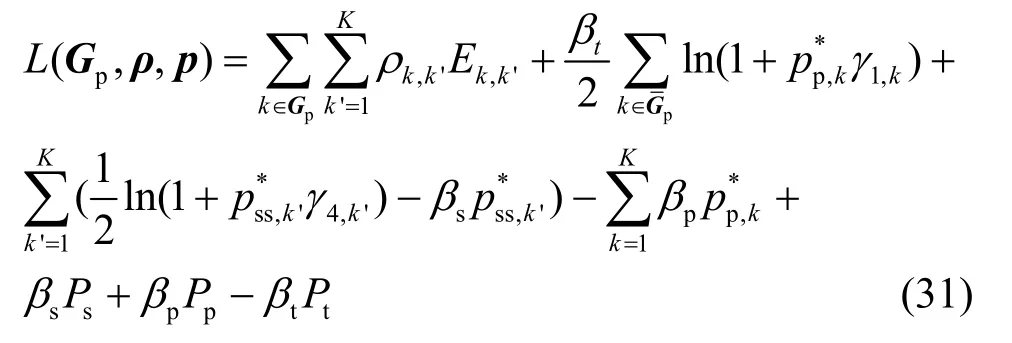
其中，

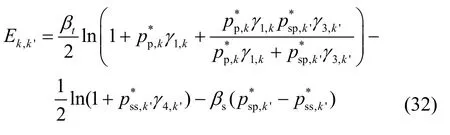
从式(31)中可以看出只有第1项跟ρk,k'有关，所以可以得到最优的子载波配对方法，对于每一个k∈Gp，只要在所有的子载波Ωs中找到一个使得Ek,k'最大的一个子载波 k ' *，即

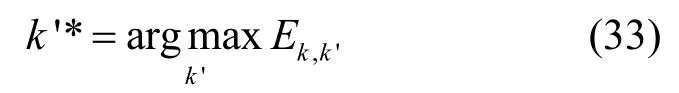
则这个子载波 '*k 与k配对：

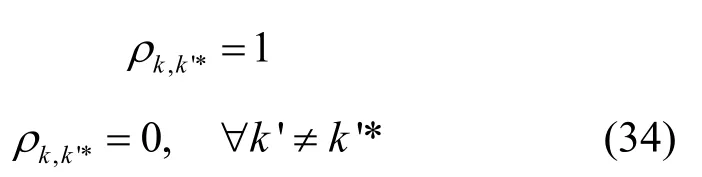
3) 最优pG：获得最优子载波配对后，把式(34)代入式(31)后可得到

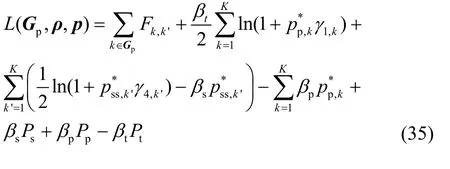
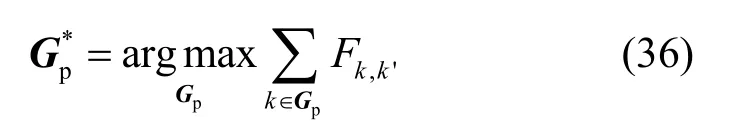
所以只要在所有的子载波 k ∈Ωp中找出所有能够使得 Fk,k'大于0的子载波，这些子载波就组成所需要的最优 Gp*。

4.4 算法比较

为了进行性能比较，同时给出其他几种子载波配对和功率分配算法。

1) 算法 1： pp,k按照不同用处分别根据PT→PR ，PT→CT的不同信道按照注水算法进行分配，psp,k'和pss,k'分别根据CT→PR和CT→CR的不同信道按照注水算法进行分配。CT的子载波和PT的子载波按照各自的信道增益大小进行配对[13]，即CT中信道增益最大的子载波和PT中信道增益最大的子载波进行配对，CT中信道增益第2大的子载波和PT中信道增益第2大的子载波配对，依次类推, 直到所有的子载波都配对完。

2) 算法2：PT和CT上子载波的功率分配按照算法1中的方法进行分配。CT的子载波和PT的子载波随机进行配对。

5 仿真结果

在仿真中，无线信道为频率选择性衰落信道，子载波数K为32。分别用来表示PT→PR、PT→CT、CT→PR和CT→CR的信道方差。假设同时假设主用户的功率 Pp= 1 0dB 。用中断速率和中断概率来表示主用户的性能，用平均速率来表示认知用户的性能。认知用户的平均速率可以表示为

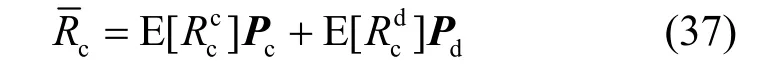
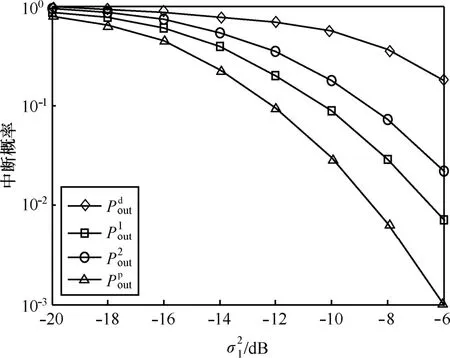
图2 主用户中断概率随信道变化（ Ps= 2 0 dB ）

图 2显示了认知用户功率 Ps= 2 0 dB ，RT=3bit/s/Hz时不同算法主用户的中断概率随着信道的变化。图中，为主用户没有认知用户接入直传时的中断概率，分别为算法 1、算法2和本文所提算法主用户的中断概率。从图中可以看出，相比于其他2种算法，本文所提的算法可以使得主用户的中断概率得到更显著地提升。当时，主用户直传时的中断概率为0.38，本文所提算法可以帮助主用户的中断概率改善到0.006 7，而其他2种算法只能帮主用户的中断概率分别改善到0.03和0.08。这是由于本文所提的算法在认知用户进行了最优的子载波分配和配对，而且对子载波的功率进行了最优分配。而其他2种算法都没有进行最优分配。导致子载波没有被最优利用，帮助主用户达到要求速率的机会变小，从而使得中断概率变大。

图3 主用户中断速率随信道变化（RT=3bit·s-1/Hz）

图 3显示了 RT=3bit/s/Hz时主用户中断速率C10%随着信道的变化。从图3中可以看出，当主用户的信道 σ12＜- 4 .6 dB ，主用户的中断速率小于其要求速率，认知用户就能接入主用户的频谱。如图3所示，随着主用户信道变差，主用户的中断速率改善得就越多。这是因为随着主用户信道的变差，主用户的中断速率就会变得越来越小，小于主用户的要求速率RT，只要认知用户有足够的功率，就能够帮助主用户达到其要求速率，接入主用户的频谱。从图中还可以看出，随着认知用户功率的变大，认知用户就能够帮助更差信道的主用户达到其要求速率RT。但是，如果主用户的信道已经足够好，当 σ12≥-4.6 dB 时，主用户的中断速率已经大于要求速率RT，则认知用户无法接入主用户的频谱。

图4显示了RT=3bit/s/Hz，=10%ε时本文算法所能帮助主用户达到要求速率 RT的区域随着认知用户功率的变化。从图中可以看出，主用户可以从本文所提的算法中获得好处。在主用户直传且没有认知用户接入时，只有主用户的信道大于-4.6dB时（即区域 I），主用户的中断速率才能达到3bit/s/Hz，当主用户的信道低于-4.6dB时（即区域II和III），主用户的中断速率不能达到要求速率。所以在这部分区域（即区域II和III），认知用户就有机会接入主用户的频谱，帮助其达到要求速率。但是认知用户的功率有限，只能帮助一部分信道条件的主用户达到要求速率，即图中的区域 II，而帮不到更差信道条件的主用户，即图中的区域III。从图中可以看出，随着认知用户功率的增大，认知用户就能够帮助更差信道的主用户达到其要求速率。这是因为随着认知用户功率的变大，就会有更多的功率帮助主用户发送信息，从而可以帮助信道更差的主用户达到要求速率。

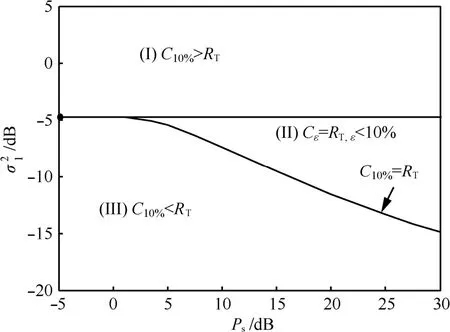
图4 临界区随功率变化（RT=3bit(s·Hz)-1）

图5显示了σ12=- 8 dB 时认知用户以协作和非协作方式接入主用户概率随着认知用户功率的变化。图中显示了不同主用户要求速率 RT=2bit/s/Hz和RT=3bit/s/Hz时的接入概率。从图5中可以看到，当 σ12= - 8 dB 时，主用户的中断速率小于 RT=2bit/s/Hz，所以当RT=2bit/s/Hz和RT=3bit/s/Hz时，主用户的中断速率小于要求速率，此时认知用户就可以接入主用户的频谱。从图5中可以看出，随着认知用户功率的增大，认知用户以协作方式接入的概率变大，而以非协作方式接入的概率变小。这是因为随着认知用户功率的增大，认知用户就能用更多的功率帮助主用户达到要求速率，从而使得以协作接入方式的概率变大。如果认知用户的功率太小，大部分情况下认知用户不能帮助主用户达到要求速率，导致认知用户以协作方式接入的概率很低，大部分认知用户以非协作方式接入主用户的频谱。从图中还可以看出要求速率RT越低，认知用户以协作方式接入的概率就越大。这是因为对于给定的功率，要求速率RT越低，认知用户就能更多地帮助主用户达到要求速率RT，所以以协作方式接入的概率就会越大。

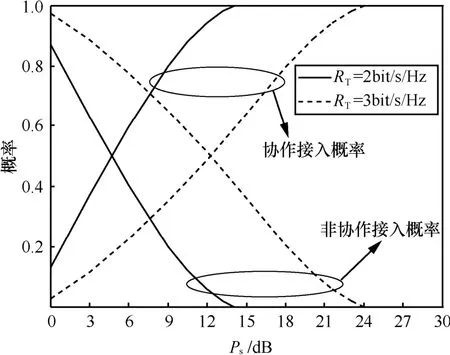
图5 认知用户接入概率随功率变化（ σ12= - 8 dB ）

图6显示了 σ12= - 8 dB 时认知用户平均速率概率随着认知用户功率的变化。从图6中可以看出，随着认知用户功率的增大，认知用户的平均速率就会变大。这是因为对于给定信道的主用户，帮助主用户达到要求速率 RT的功率是固定的，所以随着认知用户功率的增大，用来发送自己信息的功率就会变大，从而使得认知用户的平均速率变大。从图中还可以看出，RT=2bit/s/Hz认知用户的平均速率大于 RT=3bit/s/Hz。这是因为对于给定信道的主用户和给定功率的认知用户，随着 RT的变小，认知用户用来帮助达到 RT的功率就会变少，从而就会有更多的功率用来发送自己的信息，导致 RT=2bit/s/Hz的认知用户平均速率大于RT=3bit/s/Hz的认知用户平均速率。

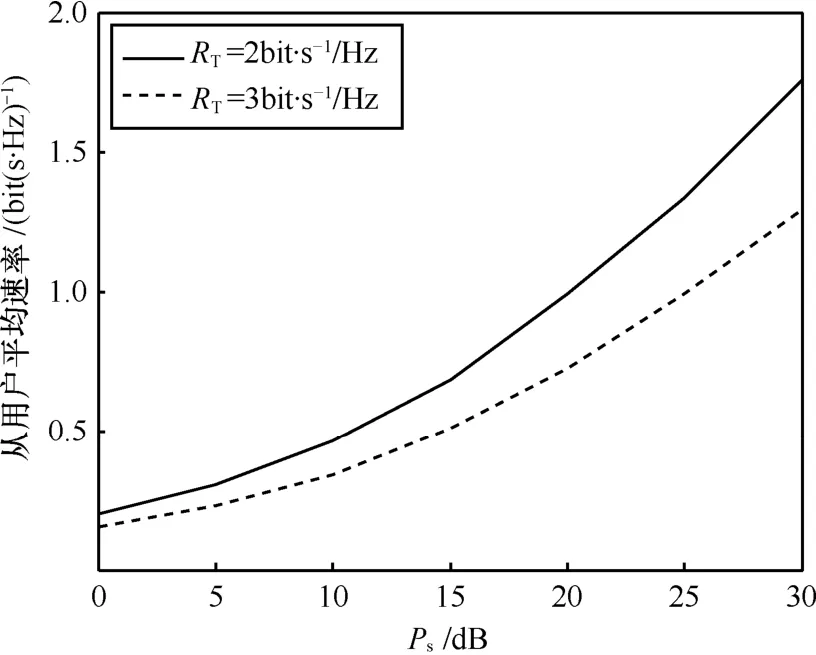
图6 认知用户平均速率随功率变化（ σ12= - 8 dB）

6 结束语

本文提出了一种基于OFDM协作中继的机会主义频谱共享协议。在该协议中，如果主用户的中断速率不能达到要求速率TR，则认知用户就能接入主用户的频谱。如果认知用户能够协作帮助主用户达到要求速率，则认知用户就以协作的方式接入主用户的频谱。在该接入方式中，认知用户通过利用一部分的子载波放大转发主用户的信息，帮助其达到要求速率。然后利用剩下的子载波来发送自己的信息。否则，如果认知用户不能帮助主用户达到要求速率，为了有效地利用频谱资源，认知用户以非协作方式接入主用户的频谱，在该接入方式中，主用户停止发送信息，认知用户利用接入获得的全部频谱发送自己的信息。由于本文所提的算法在认知用户的子载波进行了最优分配和配对，同时对子载波的功率分配进行了优化，所以相比其他算法，本文所提的算法能够获得更好的性能。仿真结果验证了本文所提频谱共享协议的有效性，并能够看出主用户和认知用户都能够从该协议中获得好处。

[1] FCC. Spectrum Policy Task Force Report[R]. 2002.

[2] MITOLA J, MAGUIRE G Q. Cognitive radios: making software radios more personal[J]. IEEE Personal Communication, 1999, 6(4):13-18.

[3] HAYKIN S. Cognitive radio: brain-empowered wireless communications[J]. IEEE Journal on Selected Areas in Communication, 2005,23(2):201-220.

[4] JOVICIC A, VISHWANATH P. Cognitive radio: an information- theoretic perspective[J]. IEEE Transactions on Information Theory, 2009,55(9):3945-3958.

[5] PANDHARIPANDE A, HO C K. Stochastic spectrum pool reassignment for cognitive relay systems[A]. IEEE Wireless Communications and Networking Conference[C]. Las Vegas, NV, USA, 2008.588-592.

[6] KANG X, LIANG Y C, NALLANATHAN A. Optimal power allocation for fading channels in cognitive radio networks: ergodic capacity and outage capacity[J]. IEEE Transactions on Wireless Communication, 2009, 8(2):940-950.

[7] KANG X, GARG H K, LIANG Y C. Optimal power allocation for OFDM-based cognitive radio with new primary transmission protection criteria[J]. IEEE Transactions on Wireless Communication, 2010,9(6): 2066-2075.

[8] LETAIEF K B, ZHANG W. Cooperative communications for cognitive radio networks[J]. IEEE: Special Issue on Cognitive Radio, 2009,97(5):878-893.

[9] SIMEONE O, STANOJEV I, SAVAZZI S. Spectrum leasing to cooperating secondary ad hoc networks[J]. IEEE Journal on Selected Areas in Communications, 2008, 26(1): 203-213.

[10] HAN Y, PANDHARIPANDE A, TING S H. Cooperative decode-andforward relaying for secondary spectrum access[J]. IEEE Transactions on Wireless Communication, 2009, 8(10): 4945-4950.

[11] HAN Y, PANDHARIPANDE A, TING S H. Cooperative spectrum sharing via controlled amplify-and-forward relaying[A]. IEEE 19th International Symposium on Personal, Indoor and Mobile Radio Communications[C]. Cannes, France, 2008. 1-5.

[12] PUN M O, MORELLI M, KUO C J. Multi-carrier Techniques for Broadband Wireless Communications: a Signal Processing Perspective[M]. London: Imperial College Press, 2007.

[13] LI Y, WANG W, KONGONG J. Subcarrier pairing for amplify-andforward and decode-and-forward OFDM relay links[J]. IEEE Communication Letters, 2009, 13(1): 209-211.

[14] HAMMERSTROM I, WITTNEBEN A. On the optimal power alloca-tion for nonregenerative OFDM relay links[A]. IEEE International Conference on Communications[C]. Istanbul, Turkey, 2006.4463-4468.

[15] YU W, LUI R. Dual methods for nonconvex spectrum optimization of multicarrier systems[J]. IEEE Transactions on Wireless Communication, 2006, 54(7): 1310-1322.

[16] DANG W B, TAO M X, MU H. Subcarrier-pair based resource allocation for cooperative multi-relay OFDM systems[J]. IEEE Transactions on Wireless Communication, 2010, 9(5):1640-1649.

[17] BOYD S, VANDENBERGHE L. Convex Optimization[M]. Cambridge: Cambridge University Press, 2004.