基于摩擦滑动的低应力区岩石变形记忆性机理

王海军 ，任旭华，陶冉冉，张继勋

(1.河海大学 水利水电学院，江苏 南京，210098；

2.西澳大学 土木与资源工程学院，珀斯 6009，澳大利亚)

岩石记忆性是指岩石储存外界对其影响信息并能在一定条件下通过某种物理量显示这些信息的特性。岩石记忆性有多种，如变形记忆性[1]、声发射记忆性(又称Kaiser效应)、离子发射记忆性和导电率记忆性等[2]。变形记忆性是指可通过岩石变形数据获取其记忆信息的特性，与Kaiser效应通过声发射获取记忆信息具有相似性。以单轴循环压缩试验为例，当后续加载应力超过先期加载应力最大值时，表现为应变曲线发生变化，由变化点得到先期加载最大应力信息，此为变形记忆性；若初始加载位于裂纹初始应力以上的应力区，应力达到先期加载最大应力时，声发射现象明显增加，此为Kaiser效应。地应力大小及方向的准确测量对于地震预报及各种地下工程的开挖设计具有重要意义[3]，初始地应力信息同样储存在岩芯中。变形率变化法(Deformation rate analysis，DRA)和声发射法(Acoustic emission，AE)是分别基于岩石变形记忆性和Kaiser效应获取地应力信息的方法。与ISRM推荐且应用最为广泛的水力致裂法和套芯应力解除法不同，DRA法及AE法通过在室内试验室对岩芯试样进行循环单轴压缩试验实现地应力测量。岩石试样可来自前期探洞开挖积累下的岩块或者岩芯。具有简易、经济、高效率的优势；且可进行大量的实验，用于统计分析以提高结果的精确度；同时，不受岩石参数各向异性的影响。岩石变形记忆性及DRA法被提出后，在日本[4-9]、俄罗斯[2]、澳大利亚[10-12]和中国台湾[13-14]有大量研究与应用；韩国、中国大陆[15]有少量研究。其中绝大部分研究重点为其物理现象特征或地应力测量的应用，涉及其形成机理的研究较少。Yamamoto等[1]在1990年提出DRA法时推断岩石变形记忆性的力学机理与Kaiser效应一样，为岩石内部新微裂纹的产生和原有微裂纹扩展。他们认为微裂纹扩展所造成的非线性应变包含可逆应变和不可逆应变2部分。在不改变微裂纹尺寸的情况下所产生的非线性应变都属于可逆应变。在连续加载中，应力超过初始加载最大应力时，新裂纹产生，已有裂纹扩展，所造成的应变为不可逆应变，进而形成变形记忆性。部分研究者[16]沿用了此描述。基于Kuwahara等[17]的剪切裂纹理论模型，Tamaki等[18]指出当加载应力低于历史应力最大值时，非弹性应变与应力呈线性关系。当加载应力超过该方向历史应力最大值时，应力-应变曲线的斜率将产生变化，造成变形记忆性。Tamaki等[19]和Yamamoto等[5]采用了与Tamaki等[18]类似的解释。Yamamoto[6]于2009年进一步指出当加载应力大于该方向初始加载应力最大值时，应变差对应力的微分值变为负值，进而产生岩石变形记忆性，并认为其原因为：(1)当超过历史最大应力值时，微裂纹将产生；(2)新微裂纹的产生会造成非弹性应变率增加。Hunt等[10,20]认为DRA折点是Kaiser效应的一个表现。他们基于PFC2D软件，对Kaiser效应和岩石变形记忆性进行了模拟。基于模拟结果，确认Kaiser效应与微裂纹的产生和扩展有关，指出当初始加载应力小于微裂纹初始应力时，岩石变形记忆性并不存在。由以上研究可知：研究者基本遵从一种模式来解释岩石变形记忆性的形成机理，伴随加载应力增高，微裂纹的产生及扩展将造成非弹性应变率增加并表现在应力-应变曲线的变化上，从而形成岩石变形记忆性。但是，大量研究[1,2,10,13]表明：岩石变形记忆性在低于裂纹初始应力的低应力区仍然存在。在此低应力区域，微裂纹产生及扩展模型并不起作用。对物理现象内在机理的正确把握是人们理解及利用这一外在现象的基础。变形记忆性机理研究的缺失严重阻碍着人们对岩石变形记忆性的正确认识及对DRA法应用技术的改进与推广。本文作者认为微裂纹的产生及扩展前的裂纹及颗粒接触面间的摩擦滑动为低应力区变形记忆性的形成机理。为验证此机理，首先综述了裂纹初始应力值的相关研究及已有研究中低应力区存在岩石记忆性的证据，同时，通过物理实验验证了低应力区岩石记忆性的存在性。基于接触面摩擦滑动理论，采用Hook体和圣韦南体(St.V体)组合建立了单接触面上摩擦滑动的基本单元；最终建立含有多裂纹及颗粒接触面的理论模型，并分析其力学特性及岩石变形记忆性的表现，进而验证摩擦滑动可以产生低应力区岩石记忆性。

1 DRA法及低应力区变形记忆性

1.1 DRA法

岩石所储存信息一般是通过实验室内单轴压缩实验获得。最直接方法是检测单轴压缩实验的应力-应变曲线的斜率变化，但是识别难度很高，常不可靠[1]。为解决此问题，Yamamoto等[1]于1990年提出了变形率变化法。首先定义单轴循环压缩实验中的应变差为：

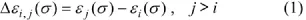
式中：εi(σ)和 εj(σ)分别代表第i次和第j次加载中的轴应变；σ为相应的应力。压应力及压应变为正。式(1)消除了连续2次压缩应变曲线中的可逆应变部分，得到非可逆应变差。应变差及变形率变化法描述如图1所示。从图1可见：应变差-应力曲线(DRA曲线)出现1个折点(DRA折点)，对应的应力σDRA即为试样在加载方向上所记忆的历史最高应力。

图1 应变差及变形率变化法Fig.1 Illustration of deformation rate analysis (DRA)

采用DRA法进行地应力测量时，一个基本假设是σDRA对应于试样轴向方向的正应力分量。因此，只需测出同一区域岩芯6个不同方向的正应力分量，即可计算出地应力状态。

地应力真实值一般未知，因此，在研究岩石记忆性时，研究者一般采用一次预加载(多为单轴压缩)以形成可知的记忆信息(或对地应力进行模拟)。此时，DRA法所得σDRA对应轴方向预加载的最大应力。

1.2 低应力区变形记忆性

岩石在单轴压缩下的变形及破坏过程在近几十年得到大量研究。一般认为，单轴压缩下岩石应力-应变曲线可分为5个阶段[21-22]：(1)裂纹闭合阶段；(2)线弹性变形阶段；(3)裂纹产生及稳定扩展阶段；(4)裂纹非稳定扩展阶段；(5)破坏或峰后软化阶段。(2)和(3)阶段的分界点称为裂纹初始应力。研究表明：裂纹初始应力一般为试样单轴抗压强度(Unconfined compression strength,σUCS)的30%～60%[21-23]。在低于裂纹初始应力的应力区，并不发生微裂纹的产生及扩展，此区域为低应力区。

如前所述，大部分文献将岩石变形记忆性的形成归因于新裂纹的产生及已有裂纹扩展。若此模型成立，与Kaiser效应一样，岩石变形记忆性应该存在于阶段(3)和(4)中，即至少大于30%σUCS的应力区间。但是，实验表明：在低应力区仍然存在岩石变形记忆性。

Yamamoto等[1]证实DRA法可以从花岗闪长岩的岩芯试样中测出1～6 MPa的地应力；Seto等[16]的实验结果表明：当历史最大应力小于单轴抗压强度的15%时，岩石仍然具有变形记忆性。Hunt等[10,13]的实验表明：岩石记忆性存在于低于单轴抗压强度的20%的应力区域。Yamshchikov等[2]指出岩石变形记忆性在弹性变形区仍然存在。

1.3 实验验证

试样材料为砂岩，取自于澳大利亚北部一矿场76 mm标准岩芯。试样为圆柱体，上下表面平整度为0.01 mm，如图2所示。试样从岩芯钻取后，在常温条件下放置时间为7 d。试样密度为2.85 t/m3, 长度为39.9 mm, 直径为18.3 mm，弹性模量为44 GPa，σUCS大于80 MPa。采用4对应变片采集应变数据。4对应变片在圆柱试样侧表面按照0°，90°，180°和270°的顺序黏贴在试样中间。加载过程由伺服加载控制系统控制，采用位移加载控制模式，为0.14 mm/min，加卸载速度相同。加载及数据采集系统如图2所示。

图2 砂岩试样及加载仪器Fig.2 Sandstone sample and loading machine

图3所示为实验的加载方式。从图3可以看出：实验采用三次循环单轴压缩。预加载最高应力σp为8.3 MPa(＜10.4%σUCS)，用来形成试样记忆信息。第2和3次称为测量加载，为DRA法中的Δε2,3(σ)提供应力-应变数据，用来获取试样对σp的记忆信息。测量加载一般为连续加载，最高应力σm相同，本实验中为75 MPa。

应力-应变曲线如图4所示，从应力-应变曲线上很难识别记忆信息。DRA曲线如图5所示。从图5可见：在8.3 MPa附近有清晰折点(箭头标注)，由此证明在历史应力小于10.4%σUCS的应力区域内，岩石仍然有变形记忆性。

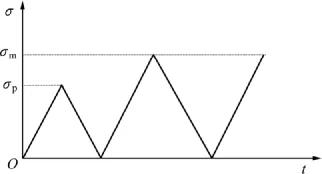
图3 加载方式Fig.3 Loading cycles

图4 砂岩试样的应力-应变曲线Fig.4 Strain-stress curve of sandstone sample

图5 砂岩试样的DRA曲线Fig.5 DRA curve of sandstone sample

2 基于摩擦滑动的理论模型

2.1 接触面的摩擦滑动

岩石是一种含有大量随机分布微裂纹接触面及颗粒接触面的材料。考虑一个单位体积的此类材料的平均应力-应变状态[24]为：

式中：σik为单位体积所受应力张量；ε0ik和σ0ik分别为弹性基质的应变与应力张量，并不受微裂纹及颗粒接触面的影响；ni为微裂纹及颗粒接触面外法线单位矢量；Vi是沿接触面的应变积分；α代表微裂纹或颗粒接触面序号。

由式(2)可知：含有微裂纹及颗粒接触面的弹性材料应变包含2部分：一部分为弹性基质产生，另一部分为接触面产生。影响第2部分的力学行为的因素很多，如微裂纹的方向和尺寸等。在低应力区，在加载作用下，裂纹及颗粒接触面产生摩擦滑动，并不造成微裂纹的产生与扩展[25]。本研究将低应力区岩石变形记忆性的产生机理归为摩擦滑动。基于以上理论，采用Hook体及St.V体的组合构建模型，实现对裂纹及颗粒接触面摩擦滑动的模拟。

2.2 基本单元模型

图6所示为含有单接触面的单位体积岩石的基本单元模型。其包括串联的2部分：一是为上部Hook体，用来模拟弹性基质的变形；二是Hook体与St.V体并联，用于模拟接触面的摩擦滑动对总应变的贡献。为了简便，本研究用“||”表示并联，第2部分称之为“Spr||St.V”体。在“Spr||St.V”体中，St.V体用来模拟摩擦滑动，当其承受应力超过黏聚力时，将开始滑动并保持应力值不变。k2为顶部串联Hook体刚度；k1为并联Hook体刚度；c1为St.V体的黏聚力。

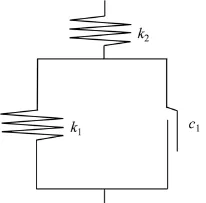
图6 基本单元模型Fig.6 Basic element

Hook体 2 与“Spr||St.V”体串联，因此，两者应力相同，模型应变为两者应变之和：

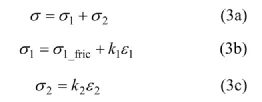
对于St.V体，有静止和滑动2种状态：滑动状态：

静止状态：

式中：σ为加载应力；ε为模型总应变；σ2和ε3分别为Hook体2的应力和应变；σ1和ε1分别为“Spr||St.V”体的应力和应变。σ1_fric是St.V体的应力，当|σ1_fric|＜c1时，“Spr||St.V”体被St.V体锁定，保持初始应变ε1(0)不变。

数值试验的加载方式如图3所示，加载应力为时间的函数。预加载最高应力值σp，用以形成记忆信息；后2次为测量加载，最大值为σm(σm＞σp)。2次测量加载的应变差Δε2,3(σ)曲线为DRA曲线。

数值实验结果表明：基本单元中Hook体并不影响其变形记忆性，随着加载区域的不同，基本单元的DRA曲线最多可出现2个折点，其对应的应力值按其出现顺序记为σDRA1和σDRA2，如图7和8所示。从图7和图8可见：

(1)当σp＜σm＜c1时，“Spr||St.V”体未滑动，无DRA折点，模型无记忆性；当2c1＜σp＜σm时，2次测量加载应力-应变曲线为完全重合的循环加卸载滞回环，此时也没有DRA折点。

(2)当c1＜σp＜σm＜2c1时，如图7 所示，DRA曲线有1个折点，此折点对应应力值σDRA1=σp。在此加载区域里，DRA法精确测出了预加载应力值。

(3)当c1＜σp＜2c1＜σm时，DRA曲线如图8所示，DRA曲线存在2个折点：第1个折点为σDRA1=σp，是对预加载应力的记忆；第2个折点为σDRA2=2c1，是对2倍黏聚力的记忆，此折点与变形记忆性无关。

图7 σp/c1=1.5和σm/c1=1.8时的DRA曲线Fig.7 DRA curve under condition of σp/c1=1.5 and σm/c1=1.8

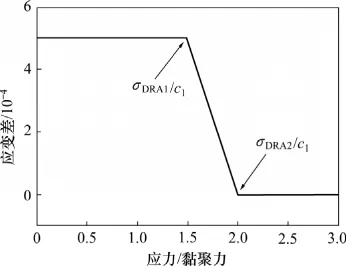
图8 σp/c1=1.5和σm/c1=3时的DRA曲线Fig.8 DRA curve under condition of σp/c1=1.5 and σm/c1=3

2.3 多接触面的摩擦滑动模型

含有n个裂纹及颗粒接触面的单位体积岩石材料的理论模型如图9所示。不考虑接触面之间的相互影响，由式(2)可知：对基本单元采用串联方式组合进行含有多裂纹及颗粒接触面岩石材料的模拟：

图9 含多接触面的理论模型Fig.9 Model for rock with many interfaces

式中σ为施加应力；α为接触面序列数。每个接触面的力学性质符合式(3a)～(3f)。

在数值分析中，选择n=500。由基本单元可知：黏聚力对DRA折点有控制作用，本研究选用均匀分布与正态分布2种分布的黏聚力。其均值和标准差设置相同，用以比较2种分布对结果的影响。多接触面模型的其余参数都相同。加载方式如图3所示。黏聚力均匀分布的范围为0～5 MPa；2种分布均值为2.505 MPa，标准差为1.444 8 MPa；正态分布如图10所示。

典型应力-应变曲线如图11(a)和12(a)所示，所对应的DRA曲线如图11(b)和12(b)所示。结果如下：

(1)多裂纹及颗粒接触面模型可形成下折的DRA曲线，即可产生变形记忆性。同时，黏聚力的分布范围的增大拓宽了模型变形记忆性的可记忆范围，DRA折点存在于最小黏聚力到2倍最大黏聚力之间。在此区间，DRA法可精确测出预加载应力。

(2)与基本单元模型相比，多接触面模型中由于接触面数目增加，DRA曲线在折点前为水平线，下折后的曲线部分呈现光滑下凹的特性，此特性和试验中DRA曲线特性相吻合(图5)。

(3)黏聚力的正态分布及均匀分布并不影响DRA曲线的形状，如图11(b)和12(b)所示。

图11 黏聚力均匀分布下的结果Fig.11 Results under uniformly distributed cohesions

图12 黏聚力为正态分布时的结果Fig.12 Results under normally distributed cohesions

3 结论

(1)岩石微裂纹产生及扩展并不能解释低应力岩石变形记忆性，本研究给出低应力区岩石存在变形记忆性的实验证据，并提出了岩石内部原有微裂纹及颗粒接触面上的摩擦滑动为低应力区形成变形记忆性的机理，揭示了岩石对于所承受加载应力包括地应力具有普遍记忆性的深层原因。

(2)基于摩擦滑动理论，构建了模拟单接触面摩擦滑动的基本单元。结果表明：在一定条件下，基本单元可以形成变形记忆性，记忆范围位于1～2倍黏聚力之间的应力区域内。

(3)基于基本单元，构建多接触面理论模型，结果证明模型可形成记忆性。DRA曲线在DRA折点前为水平线，折点后为光滑下凹曲线，与物理实验中DRA曲线特性吻合。同时，黏聚力不同分布规律并不影响DRA曲线形状。

(4)低应力区微裂纹及颗粒接触面的摩擦滑动可以形成岩石变形记忆性。下一步工作将在模型中纳入时间因子，以研究变形记忆性的时间效应如失忆性。

致谢：

本文作者感谢国家留学基金委提供国家建设高水平大学公派项目奖学金，感谢澳大利亚地质力学中心(Australian Centre for Geomechanics)提供奖学金支持作者在西澳大学完成相关研究。验证实验由西澳大学Ariel Hsieh完成，数据由西澳大学Ariel Hsieh，Arcady Dyskin和Phil Dight提供，在此表示感谢。

[1]Yamamoto K, Kuwahara Y, Kato N, et al.Deformation rate analysis: A new method for in situ stress estimation from inelastic deformation of rock samples under uni-axial compressions[J].Tohoku Geophysical Journal, 1990, 33:127-147.

[2]Yamshchikov V S, Shkuratnik V L, Lavrov A V.Memory effects in rocks (review)[J].Journal of Mining Science, 1994, 30(5):463-473.

[3]Fairhurst C.Stress estimation in rock: A brief history and review[J].International Journal of Rock Mechanics and Mining Sciences, 2003, 40(7/8): 957-973.

[4]Yabe Y, Yamamoto K, Sato N, et al.Comparison of stress state around the Atera fault, central Japan, estimated using boring core samples and by improved hydraulic fracture tests[J].Earth,Planets, and Space, 2010, 62: 257-268.

[5]Yamamoto K, Yabe Y.Stresses at sites close to the Nojima Fault measured from core samples[J].Island Arc, 2001, 10(3/4):266-281.

[6]Yamamoto K.A theory of rock core-based methods for in-situ stress measurement[J].Earth Planets Space, 2009, 61(10):1143-1161.

[7]Yabe Y, Song S R, Wang C Y.In-situ stress at the northern portion of the Chelungpu fault,Taiwan, estimated on boring cores recovered from a 2-km-deep hole of TCDP[J].Earth Planets Space, 2008, 60(8): 809-819.

[8]Yabe Y, Omura K.In-situ stress at a site close proximity to the Gofukuji Fault, central Japan, measured using drilling cores[J].Island Arc, 2011, 20(2): 160-173.

[9]Seto M, Villaescusa E, Utagawa M, et al.In situ stress evaluation from rock cores using AE method and DRA[J].Shigen-to-Sozai,1998, 114(12): 845-855.

[10]Hunt S P, Meyers A G, Louchnikov V.Modelling the Kaiser effect and deformation rate analysis in sandstone using the discrete element method[J].Computers and Geotechnics, 2003,30(7): 611-621.

[11]Dight P M, Dyskin A V.On the determination of rock anisotropy for stress measurements[C]//SHIRMS 2008.Perth, Australia,2008: 575-585.

[12]Dight P.Stress states in open pits.Keynote lecture-Slope Stability in Mining and Civil Engineering(Report)[R].2011.Perth.

[13]Chan S C.Investigating the laboratory experiments to estimate pre-stress on Changchikeng sandstone[D].Tainan: National Cheng Kung University, 2008: 57-85.

[14]Wu J H, Jan S C.Experimental validation of core-based pre-stress evaluations in rock: A case study of Changchikeng sandstone in the Tseng-wen reservoir transbasin water tunnel[J].Bulletin of Engineering Geology and the Environment, 2010,69(4): 549-559.

[15]谢强, 邱鹏, 余贤斌, 等.利用声发射法和变形率变化法联合测定地应力[J].煤炭学报, 2010, 35(4): 559-564.XIE Qiang, QIU Peng, YU Xian-bin, et al.Initial-stress measurements with AE and DRA combined technique[J].Journal of China Coal Society, 2010, 35(4): 559-564.

[16]Seto M, Nag D K, Vutukuri V S.In-situ rock stress measurement from rock cores using the acoustic emission method and deformation rate analysis[J].Geotechnical and Geological Engineering, 1999, 17(3): 241-266.

[17]Kuwahara Y, Yamamoto K, Hirasawa T.An experimental andtheoretical study of inelastic deformation of brittle rocks under cyclic uniaxial loading[J].Tohoku Geophys J, 1990, 33(1): 1-21.

[18]Tamaki K, Yamamoto K, Furuta T, et al.An experiment of in situ stress estimation on basaltic rock core samples from Hole 758A,Ninetyeast Ridge, Indian Ocean[C]//Proc ODP, 121: College Station.TX(Ocean Drilling Program), 1991: 697-717.

[19]Tamaki K, Yamamoto K.Estimating in situ stress field from basaltic rock core samples of Hole 794C, Yamato Basin, Japan Sea[C]//Proceedings of the Ocean Drilling Program.San Francisco, 1992: 1047-1059.

[20]REN Xu-hua, WANG Ha-jun, ZHANG Ji-xun.Numerical study of the AE and DRA method in sandstone and granite in orthogonal loading directions[J].Water Science and Engineering,2012, 5(1): 93-104.

[21]Martin C D.The strength of massive Lac du Bonnet granite around underground openings[D].Manitoba: University of Manitoba, 1993.

[22]Eberhardt E, Stead D, Stimpson B, et al.Identifying crack initiation and propagation thresholds in brittle rock[J].Canadian Geotechnical Journal, 1998, 35(2): 222-233.

[23]Alkan H, Cinar Y, Pusch G.Rock salt dilatancy boundary from combined acoustic emission and triaxial compression tests[J].International Journal of Rock Mechanics and Mining Sciences,2007, 44(1): 108-119.

[24]Salganik R L.Overall effects due to cracks and crack-like defects[C]//Proceedings of First International Symposium on Defects and Fracture.Tuczno, Poland: 1982: 199-208.

[25]David E C, Brantut N, Schubne A, et al.Sliding crack model for nonlinearity and hysteresis in the uniaxial stress–strain curve of rock[J].International Journal of Rock Mechanics & Mining Sciences, 2012, 52: 9-17.