一种验证网格质量与CFD计算精度关系的方法

董亮，刘厚林，谈明高，王勇，王凯

(江苏大学 流体机械工程技术研究中心，江苏 镇江，212013)

网格质量对计算的精度和效率有显著的影响。劣质单元的出现将导致在CFD计算时出现刚度矩阵病态，严重影响计算结果的精度，甚至可能导致无法计算[1-3]。因此，在CFD计算之前，需要对网格质量进行评估，以判断其是否能够满足求解器要求。四面体网格因其对复杂边界有较强的适应性，已成为CFD数值计算中最常用的网格单元。虽然公认正四面体是四面体单元的理想形状，但长期以来，对四面体单元质量的度量或评判并没有公认的或绝对的标准[4-6]。在计算几何和计算科学等领域，所谓“高质量”单元并没有一个明确的定义，而是将与规则形状偏离较大的单元认为是“劣质”单元，而将接近于规则形状的单元认为是“高质量”单元。目前，大多数针对网格质量衡量准则的研究工作，主要集中在各衡量准则对于劣质单元的评判效果以及它们是否等价等方面[7-10]。如Parthasarathy等[11]研究了7种常用的网格质量衡量准则判别劣质单元的敏感性问题。Liu等[12]对3种网格质量衡量准则之间的关系进行了研究，认为这些网格质量衡量准则在某种意义上是相互等价的，即对形状较差单元，若一种度量值趋于0，则其他2种度量值也趋于0。文献[13]也认为这几种衡量准则是相互等价的，并通过算例表明，采用任何一种衡量准则优化，都可以获得更高质量的网格。聂春戈等[14]通过数值试验发现，采用不同的准则评判单元形状的变化,有可能产生矛盾的评判效果，从而影响网格质量优化的过程和结果。然而，网格单元质量的提高与CFD计算精度提高的关系研究较少。本文作者以90°弯管为研究对象，探讨构建网格独立解的方法，并对比4种网格质量衡量准则与计算精度的关系。

1 四面体质量衡量准则

判断单元质量最直接的标准是数值计算模块利用该单元进行求解时的精度和速度。这个衡量标准并不适合直接作为网格生成和网格优化调整的准则，因此，从不同角度考虑的四面体单元质量衡量准则被提出。一般而言，一个合理的四面体网格质量衡量准则应满足以下原则：

(1)单元的平移、旋转、均匀缩放都应不改变其度量值；

(2)退化单元(单元体积为0)的质量度量值为0，正四面体的度量值最大为1；

(3)反转单元(单元体积为负)的度量值为负；

(4)衡量准则应为四面体各个节点坐标的函数，并且能够反映单元形状的变化；

(5)能够检测出易导致计算发散的劣质单元。

各种质量衡量准则如表1所示。其中，QEVS和QEAS 2种网格质量衡量准则为商业网格划分软件GAMBIT[15]中EquiSize Skew和EquiAngle Skew准则的变形，它们分别用来验证单元等尺寸和等角度的失真程度。同时，本文提出了QNEW1和QNEW2 2种质量衡量准则，用来验证单元的形状和尺寸特性，大量数值实验表明它们满足作为一个合理质量衡量准则的所有特性。衡量准则的度量值越大，说明单元质量越好；且当单元为正四面体时度量值达到最大值1，单元为退化单元时度量值达到最小值0。

表1 各种单元质量衡量准则Table1 Different quality metrics

2 网格独立解

2.1 计算模型及数值方法

为了验证网格质量衡量准则与计算精度之间的关系，以90°弯管作为研究对象，其几何尺寸如图1所示[16]。为了便于分析，将弯管分成上游直线段、弯曲段和下游直线段3部分。并定义弯曲段的主流入口截面处θ=0°，弯曲段出口截面处θ=90°，坐标系原点O位于圆管的圆心，有关90°弯管具体参数如表2所示。

图1 90°弯管结构示意图Fig.1 Sketch of 90°bending duct and definition of coordinates

应用商业软件Fluent，计算采用RNGk-ε湍流模型，非耦合隐式方案进行求解。通过有限体积法进行空间离散，对控制方程中的源项和扩散项应用二阶中心差分格式，对流项应用二阶迎风格式，采用SIMPLE算法来实现速度和压力的耦合求解。具体边界条件如下。

进口边界条件：流体均匀地进入管道中，初始速度为1 m/s。

出口边界条件：压力出口。

壁面条件：固体壁面采用边壁无滑移条件；靠近固体边界区域，采用标准壁面函数处理。

表2 90°弯管参数Table2 90° bending duct parameters

2.2 获得网格独立解的方法

2.2.1 算法流程

本文网格独立解的获得是基于各套网格数值解计算得到的相应速度误差。通过调整网格步长使网格加密，然后比较相邻网格中各单元的速度，进而得到相应的误差。当所有单元的平均相对误差小于某一规定值ε时，即可认为计算结果是网格独立解。具体过程如下。

步骤1 生成初始四面体(作为第k套网格)，进行数值计算并记录网格中各节点的速度(作为第k套网格数值解)；

步骤2 按照第k套网格单元数的1.3倍增加网格单元数作为第k+1套网格单元数，进行数值计算并记录网格中各节点的速度(作为第k+1套网格数值解)；

步骤3 采用三维线性插值算法将k+1套数值解映射到k套的数值解中，获得第k+1套网格在第k套网格中相应的数值解；

步骤4 计算第k+1套与第k套的速度相对误差：

其中：vk，i为第k套网格节点i的速度；vK+1，i为第k+1套网格映射后在节点i处的速度；N为k套网格节点总数。

步骤5 如果小于给定的误差ε(本文取ε=2%)，那么就认为第k套网格计算结果是网格独立解，否则重复步骤1～4。

2.2.2 映射获得相邻数值解的算法

将k+1套网格的数值解映射到k套数值解中，获得第k+1套网格在第k套网格中相应数值解的具体过程如下。

步骤1 将k套网格中的所有节点的坐标存储到Φ1中；

步骤2 将k+1套网格中的所有节点的坐标和速度存储到Φ2中；

步骤3 依次读取Φ1中的节点P，并以该节点为球心，R为半径，找出Φ2中所有位于该球内的节点，如果Φ2中存在于P点重合的节点，则将其速度存储到Ω中，并接着执行步骤7；

步骤4 判断位于球内节点的个数，若小于给定值N，则继续增加区间，直到位于球内的节点数大于N为止；

步骤5 若位于球内的节点数大于N，则只取最近的N个节点；

步骤6 采用三维线性插值算法计算出节点P在k+1套网格相同位置的速度，并将其存储到Ω中；

步骤7 重复步骤3～6，直到Φ1中没有节点为止。

其中R和N为预先给定值，从模型尺寸以及计算精度考虑，本文取R=0.015m，N=20。

2.3 结果统计及分析

图2所示为90°弯管在不同网格等级下的网格单元以及节点数，其中相邻网格的单元数比值大约为1.3。各套网格的最差单元质量和平均网格单元质量如图3所示。从图3可以看出，随着单元数的增加，网格最差单元质量以及平均网格质量都随之增加。

图4所示为相邻网格之间计算得到的速度相对误差，从图4可以看出，网格数较小时，相邻网格之间速度存在较大的误差，如第2套网格与第1套网格的速度相对误差达到24.59%，然而，随着网格数的增加，相邻网格之间的速度相对误差逐渐减少，第10套网格与第9套网格之间的速度相对误差为1.64%，小于给定的误差2%，因此，可以将第9套网格计算得到的数值解作为90°弯管的网格独立解。

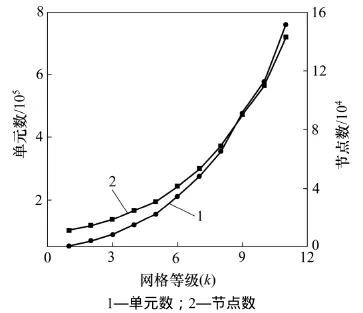
图2 网格划分结果Fig.2 Mesh generation results

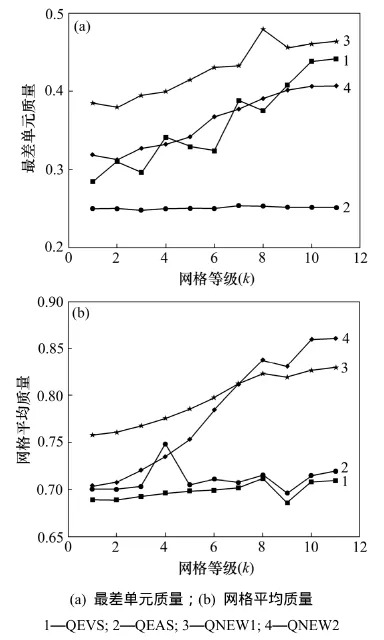
图3 各网格等级质量Fig.3 Quality for different levels of mesh

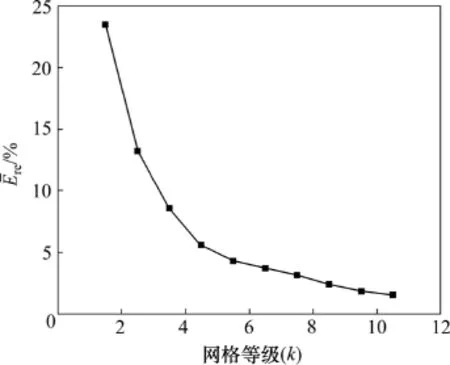
图4 相邻网格之间计算得到的速度相对误差Fig.4 Average relative error between adjacent meshes

3 分析与讨论

3.1 验证方法

将单元质量的度量值以及相对于独立解的速度相对误差组成一个数据库，通过研究该数据库来获得网格质量衡量准则与计算精度之间的关系。具体步骤如下。

步骤1 获得不完善网格(前8套网格)中各单元的网格质量度量值(采用表1中的4种衡量准则分别进行计算)；

步骤2 获得不完善网格中各单元相对于独立解(第9套网格)的速度相对误差(与2.2节方法一致)；

步骤3 将算例中所有单元质量的度量值和相对于独立解的误差建立一个数据库；

步骤4 按照单元的速度相对误差从小到大顺序对数据库中的数据重新排列；

步骤5 将该数据库分为若干区间(本文取20)，并计算各个区间的统计数据值(本文采用该区间中数据的平均值或最小值)。

3.2 结果统计

图5所示为将前8套网格中所有单元质量度量值和计算误差建立的1个数据库，获得4种质量衡量准则与计算精度之间的关系。从图5可以看出：当采用区间最小值表示该区间的趋势时，这4种衡量准则与计算精度没有任何规律。而当以区间平均值表示该区间的趋势时，QEVS和QEAS这2种准则在误差较小的区间内(＜0.1)，与计算精度有较好的关系(随着误差的增加，单元的度量值降低)；然而在其他区间内，随着误差的增加，它们的度量值出现了波动，也就是说在网格生成或优化的过程中，使用这2种准则可能会使网格朝着误差较大的方向进行优化。对于QNEW1和QNEW2，除了某些区间外(0.1＜＜0.12)，在其他区间内，它们与计算精度具有较好的关系，尤其在计算误差较大的区间内(＞0.15)，变化更加明显。因此，QNEW1和QNEW2这2种衡量准则能够较好地区分计算误差较大的单元，更加准确地指导网格的生成。

图5 网格质量衡量准则与计算精度之间的关系Fig.5 Relationship between four metrics and errors

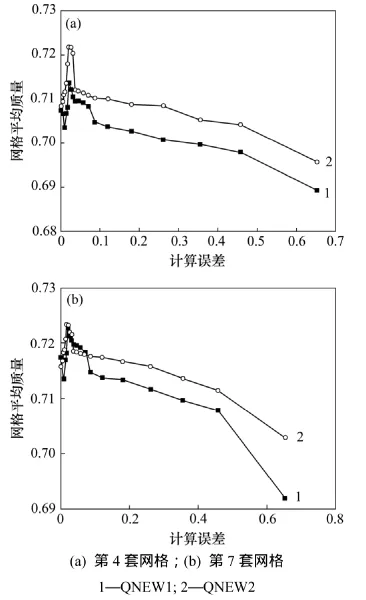
图6 QNEW1与QNEW2计算精度之间的关系Fig.6 Relationship between two metrics (QNEW1 and QNEW2)and errors

为了进一步验证QNEW1和QNEW2这2种衡量准则与计算精度之间的关系，以第4套与第7套算例作为研究对象，且采用区间的平均值表示该区间的趋势，结果如图6所示。由图6可知：两者的变化规律与图5(c)和5(d)变化规律基本一致，都是在误差较大的区间内，QNEW1和QNEW2 2种衡量准则与计算精度有较好的关系，且在相同误差的情况下，QNEW2的度量值大于QNEW1的度量值。

4 结论

(1)提出了2种四面体网格质量衡量准则QNEW1和QNEW2，研究了它们及衡量准则QEAS，QEVS与CFD计算精度之间的关系。

(2)为了准确地验证网格质量衡量准则与计算精度之间的关系，提出了一种通过数值计算构建网格独立解的方法，由于该方法考虑了每个单元的计算误差，因而获得的独立解更加接近真实解。

[1]Munson T.Mesh shape-quality optimization using the inverse mean-ratio metric[J].Mathematical Programming, 2007, 110(3):561-590.

[2]黄晓东, 杜群贵.二维有限元网格的局部加密方法[J].华南理工大学学报: 自然科学版, 2004, 32(12): 56-60.HUANG Xiao-dong, DU Qun-gui.Local refinement of 2D finite element meshes[J].Journal of South China University of Technology: Natural Science Edition, 2004, 32(12): 56-60.

[3]Park J, Shontz S M.Two derivative-free optimization algorithms for mesh quality improvement[J].International Conference on Computational Science, 2010, 1(1): 387-396.

[4]Hetmaniuk U, Knupp P.A mesh optimization algorithm to decrease the maximum interpolation error of linear triangular finite elements[J].Engineering with Computers, 2010, 27(1):3-15.

[5]Knupp P M.Algebraic mesh quality metric[J].SIAM Journal on Scientific Computing, 2001, 23(1): 193-218.

[6]Babuska I, Flaherty J E, Henshaw W D, et al.Modeling, mesh generation, and adaptive numerical methods for partial differential equations[M].New York: Springer, 1995: 97-127.

[7]Gosselin S, Ollivier-Gooch C.Tetrahedral mesh generation using Delaunay refinement with non-standard quality measures[J].International Journal for Numerical Methods in Engineering,2011, 87(8): 795-820.

[8]Dompierre J, Vallet M G, Labbé P, et al.An analysis of simplex shape measures for anisotropic meshes[J].Computer Methods in Applied Mechanics and Engineering, 2005, 194(48/49):4895-4914.

[9]Freitag L A, Knupp P M.Tetrahedral element shape optimization via the Jacobian determinant and condition number[C]//Proceedings of the 8th International Meshing.California, 1999:247-258.

[10]董亮, 刘厚林, 谈明高, 等.离心泵四面体网格质量衡量准则及优化算法[J].西安交通大学学报, 2011, 45(11): 31-36.DONG Liang, LIU Hou-lin, TAN Ming-gao, et al.Quality measurement criteria and optimization algorithm of tetrahedral mesh for centrifugal pumps[J].Journal of Xi’an Jiao Tong University, 2011, 45(11): 31-36.

[11]Parthasarathy V N, Graichen C M, Hathaway A F.A comparison of tetrahedron quality measures[J].Finite Elements in Analysis and Design, 1993, 15(3): 255-261.

[12]Liu A, Joe B.Relationship between tetrahedron shape measures[J].BIT Numerical Mathematics, 1994, 34(2):268-287.

[13]Lo S H.Optimization of tetrahedral meshes based on element shape measures[J].Computers& Structures, 1997, 63(5):951-961.

[14]聂春戈, 刘剑飞, 孙树立.四面体网格质量度量准则的研究[J].计算力学学报, 2003, 20(5): 579-582.NIE Chun-ge, LIU Jian-fei, SUN Shu-li.Study on quality measures for tetrahedral mesh[J].Chinese Journal of Computational Mechanics, 2003, 20(5): 579-582.

[15]Fluent Inc, Gambit User’s Guide[EB/OL].[2003-12-30].http://combust.hit.edu.cn:8080/fluent/Gambit13_heop/users_guide.

[16]Taylor A, Whitelaw J H.Curved ducts with strong secondary motion: Velocity measurements of developing laminar and turbulent flow[J].Journal of Fluids Engineering, 1982, 104:350-359.