中立型双时滞微分系统Hurwitz稳定性的代数判据

员陈鑫， 蒋 威

（安徽大学 数学科学学院，安徽 合肥 230601）

中立型双时滞微分系统Hurwitz稳定性的代数判据

员陈鑫， 蒋 威

（安徽大学 数学科学学院，安徽 合肥 230601）

文章讨论了一类线性双时滞中立微分系统的渐近稳定性。首先给出系统的特征方程，进而根据相关引理得到初步判定系统的Hurwitz稳定的充分条件；并以矩阵模的半径为研究中介，通过构造矩阵的方法最终得到简单的判定系统Hurwitz稳定的判据；借助矩阵谱半径的形式给出结论，从而更加方便验证。

中立系统；代数判据；时滞；稳定性

0 引 言

时滞普遍存在于现实系统中，而且几乎在所有的系统中都在一定程度上制约着系统的结构、性质和性能，直接影响系统的结果。关于时滞微分系统的稳定性研究取得了一定的进展［1－9］。但从已有的研究成果看，关于Hurwitz稳定性的研究尚不多见。

本文考虑一类双时滞线性中立微分系统：

其中，x（t）∈Cn×1为系统的状态向量；τ1，τ2≥0为2个非负时滞常量，记τ＝max｛τ1，τ2｝；矩阵A，B1，B2，C1，C2∈Cn×n，本 文 假 定 系 统 矩 阵A为Hurwitz矩阵，即所有A的特征值都具有负实部。

1 预备知识及引理

本文分别用λj（A）和ρ（A）来记矩阵A的第j个特征根和谱半径；｜A｜表示矩阵A的模，即若矩阵A＝（aij），则定义｜A｜：＝（｜aij｜）；A≤B表示A矩阵的元素aij和B矩阵的元素bij对所有的i和j满足aij≤bij；R（s）表示复数s的实部。

利用Laplace变换容易得到中立系统（1）的特征方程为：

其中，P（s）为系统（1）的特征函数。

引理1 如果aD＝sup｛R（s）：P（s）＝0｝，且有aD＜0，那么系统（1）是渐进稳定的［1］。

引理2 假设矩阵A∈Cn×n，若有ρ（A）＜1，那么（I－A）－1存在，且有［8］：

引理3 设矩阵G，H，K∈Cn×n，如果有｜G｜≤K，则有［8］：

定理1 若矩阵A为Hurwitz矩阵，并且（4）式成立，则中立系统（1）为渐近稳定的。

证明 记ξ1（s）＝e，ξ2（s）＝，则对于 R（s）≥0，｜ξ1（s）｜≤1，｜ξ2（s）｜≤1，有

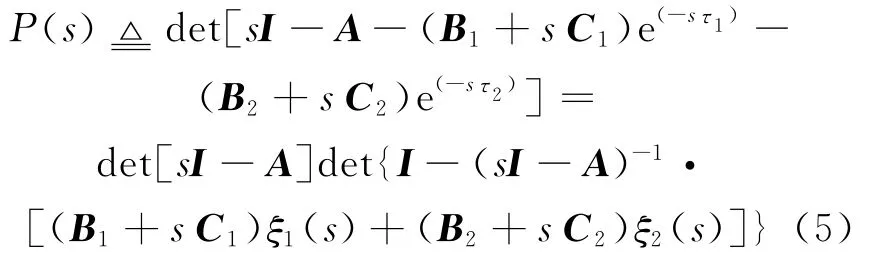
而矩阵A为Hurwitz矩阵，则有：

成立，那么对于R（s）≥0，有P（s）≠0。由引理3，对于s满足R（s）≥0，有

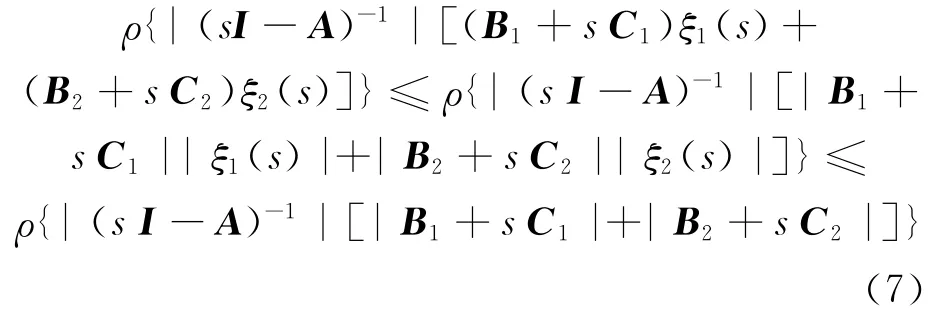
因此条件（4）成立意味着不等式（6）必然成立，即R（si）＜0，其中si为特征方程（2）的第i个特征根。假设存在一个满足特征方程（2）的特征根序列sn，满足R（sn）→0，且R（sn）＜0。因为矩阵A为Hurwitz矩阵，则A的每个特征根为：

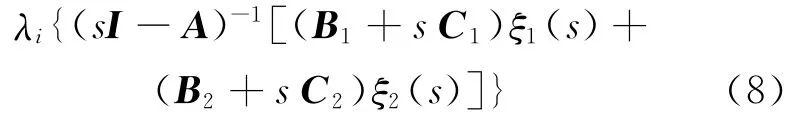
在R（s）≥0时，（8）式是解析函数，则意味着条件（4）存在ε＞0，使得：

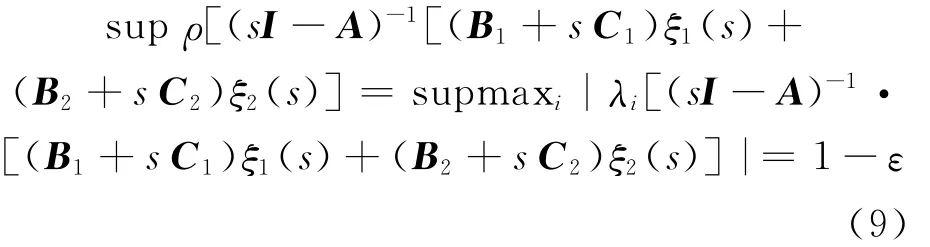
对于满足R（s）≥0的s成立。因此对于R（ξ）＝0，则有：

因为R（sn）→0，则对于给定的足够小的正数ε1＜ε，存在整数n＊，使得｜R（sn）｜足够小并且成立，对任意的n＞n＊以及R（ξ）＝0，有

进而可以得到对于n＞n＊以及R（ξ）＝0有：

当n（＞n＊）充分大时，必然有：

因此，对于R（sn）→0且R（sn）＜0，有

这与假设存在的特征根序列sn满足R（sn）→0且R（sn）＜0是矛盾的。依据引理1，定理1得证。

系统（1）中的系数矩阵A为Hurwitz矩阵，则矩阵I－A是非退化的，即（I－A）－1存在。本文定义R＝（I－A）－1（I＋A），且满足，

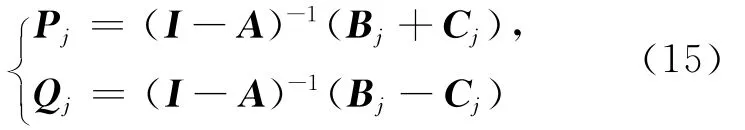
其中，j＝1，2。

引理4 若系统矩阵是Hurwitz矩阵，则对于R（s）＞0，｜z｜≤1以及j＝1，2，有

成立［7］，其中，Pj和Qj的定义参见（15）式，并且满足：

定理2 系统 （1）是渐进稳定的充分条件为矩阵A为Hurwitz矩阵，且有：

2 主要结果

假设ρ（｜R｜）＜1，根据引理2可知，（I－｜R｜）－1存在。对于整数q≥1，定义矩阵：

引理5 对于整数q≥1，Xj（q＋1）≤Xj（q），j＝1，2。

证明 根据（19）式有：

则对于任意整数q≥1，Xj（q＋1）≤Xj（q）。证毕。

引理6 假设ρ（｜R｜）＜1，那么对于任意z∈C，｜z｜≤1，整数q≥1，j＝1，2，有不等式：

成立。

证明 对于｜zR｜≤｜R｜，∀z∈C且｜z｜≤1时，有

由引理2知，（I－zR）－1存在，并且有：

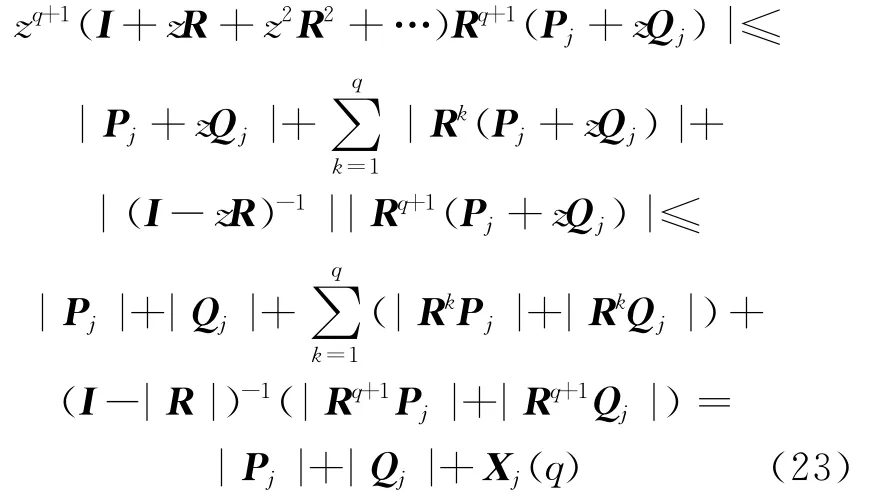
根据引理1可得，对于整数q≥1和j＝1，2有Xj（q）≤Xj（0），则（21）式成立，定理得证。

定理3 系统（1）是渐近稳定的充分条件为：矩阵A为Hurwitz矩阵，并对于整数q≥1有：

［1］Hale J，Verduyn Lunel S M.Introduction to functional differential equations［M］.New York：Springer－Verlag，1993：20－560.

［2］Lancaster P，Tismenetsky M.The theory of matrices［M］.Orlando：Academic Press，1985：124－193.

［3］Hale J K，Infante E F，Tsen F S P.Stability in linear delay equations［J］.Journal of Mathematical Analysis and Applications，1985，105（2）：533－555.

［4］Li L M.Stability of linear neutral delay－differential systems［J］.Bulletin of the Australian Mathematical Society，1988，38：339－344.

［5］Zhou X，Wei J.Eigenvalue distribution of degenerate NFDE with delay［J］.Math Appl，2002，15（2）：48－51.

［6］Wei J.Eigenvalue and stability of singular differential delay systems［J］.J Math Anal Appl，2004，297（1）：305－316.

［7］蒋 威.退化时滞微分系统［M］.合肥：安徽大学出版社，1998：55－90.

［8］郑祖庥.泛函微分方程理论［M］.合肥：安徽教育出版社，1992：121－135.

［9］王晓华，奥 顿，吴忠强，等.不确定非线性时滞系统的时滞依赖保性能控制［J］.合肥工业大学学报：自然科学版，2010，33（3）：387－390，395.

Algebraic criteria of Hurwitz－stability of neutral differential system with double time delays

YUAN Chen－xin， JIANG Wei
（School of Mathematical Sciences，Anhui University，Hefei 230601，China）

The asymptotic stability of linear neutral differential system with double time delays is investigated.The characteristic equation of the system is given，and according to related lemmas，the tentative sufficient condition of Hurwitz－stability of the system is gotten.By the method of constructing matrices，the simple delay－independent Hurwitz－stability criteria are derived in terms of the spectral radius of modulus matrices.The conclusions are drawn based on the spectral radius of modulus matrices which makes the validation easier.

neutral system；algebraic criteria；time delay；stability

O178

A

1003－5060（2012）11－1574－03

10.3969／j.issn.1003－5060.2012.11.031

2012－03－30；

2012－09－10

国家自然科学基金资助项目（11071001）；高等学校博士学科点专项科研基金资助项目（2009340111000）；安徽省高校重大资助项目（KJ2010ZD02）和安徽省高校自筹经费资助项目（KJ2012Z338）

员陈鑫（1984－），男，安徽马鞍山人，安徽大学硕士生；

蒋 威（1959－），男，安徽五河人，博士，安徽大学教授，博士生导师.

（责任编辑 闫杏丽）