基于混合二元缺向量值有理插值的图像修复

胡大海， 朱晓临

（合肥工业大学 数学学院，安徽 合肥 230009）

基于混合二元缺向量值有理插值的图像修复

胡大海， 朱晓临

（合肥工业大学 数学学院，安徽 合肥 230009）

文章提出了一种基于二元缺向量值有理插值的彩色图像修复方法，该方法将数字图像的每个像素点看成定义在一个平面域上以R、G、B为分量的一个向量，根据已知像素的变化趋势，相应地采用二元缺向量值Newton－Newton插值、Newton－Thiele插值、Thiele－Newton插值或 Thiele－Thiele插值构造向量值插值曲面，然后对插值曲面进行采样以实现修复。实验结果表明，该算法比TV方法和CDD方法修复的效果更好，所用时间更短。

二元缺向量值有理插值；混合向量值连分式插值；彩色图像修复

图像修复主要是对图像破损部分进行修复，使得在与原始图像风格保持一致的前提下，人眼觉察不到修复的痕迹。目前主要有用于修复小尺度缺损的数字图像修补（inpainting）技术和用于填充图像中大块丢失信息的图像补全（completion）技术。数字图像修补技术最早是由文献［1］引入图像处理的，文献［1］首次提出了一种利用偏微分方程，模仿职业修复者对图像进行修复，开创了偏微分方程修复图像的先河，主要采用将待修复区域外部的信息沿着轮廓法向扩散至修补区域。随后更多改进的PDE模型［2－3］被提出。但是该类方法缺乏稳定性，尤其在修复区域很大而且背景为纹理图案时，会产生模糊的现象。

图像补全技术包含以下2种方法：基于块的纹理合成技术来填充丢失信息；基于图像分解的修复技术，其主要思想是将图像分解为结构部分和纹理部分，其中结构部分用inpainting算法修补，纹理部分用纹理合成法填充。

向量值有理插值在图像处理中的应用还很少，而且主要集中在图像的放大方面。文献［4］讨论了自适应图像缩放的切触有理混合插值算法；文献［5］在行和列上分别构造一元Thiele连分式或Newton多项式，对图像进行放大；文献［6］通过在行和列上构造一元Thiele型向量连分式对图像进行放大；文献［7］通过在矩形插值模块上构造二元向量Newton－Thiele型有理插值曲面或Newton－Newton插值曲面，然后对插值曲面进行重采样实现图像缩放。而将二元向量值有理插值运用于彩色图像修复的相关研究并不多。

本文将二元混合缺向量值有理插值方法用于彩色图像的修复，将数字图像的每个像素点看成定义在一个平面域上以R、G、B为分量的一个向量，对彩色图像进行整体插值修复。

在修复过程中，将待修复区域根据不同破损特征分成若干小的矩形块，在每个小块上分别构造不同的二元混合缺向量值有理插值函数，再对插值曲面进行重采样，从而实现图像的修复。实验结果显示，本文方法不仅在修复后的视觉效果和峰值信噪比（PSNR）上都比TV方法和CDD方法优越，而且修复时间也相应地节约了很多。

1 二元混合缺向量值有理插值

1.1 二元缺向量值T－N型混合有理插值

设给定点集［8］为：

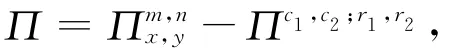
其中，＝｛（xi，yj）｜i＝0，1，…，m；j＝0，1，j＝r1＋1，…，r2－1｝。

向量数据集V＝｛vij∈Vm，n｜（xi，yj）∈Π｝，Π的结构如图1所示。

图1中，B为（c2－c1－1）×（r2－r1－1）的子矩阵，为缺失部分。构造点集Π上的二元缺向量值Thiele－Newton型混合有理插值为（1）式，使之满足R（xi，yj）＝vij，i＝0，1，…，m；j＝0，1，…，n。

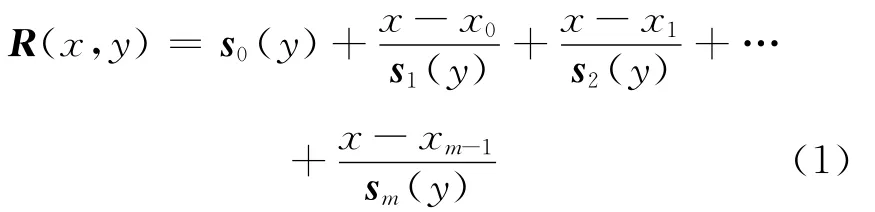
其中，当i＝0，1，…，c1，c2，c2＋1，…，m时，

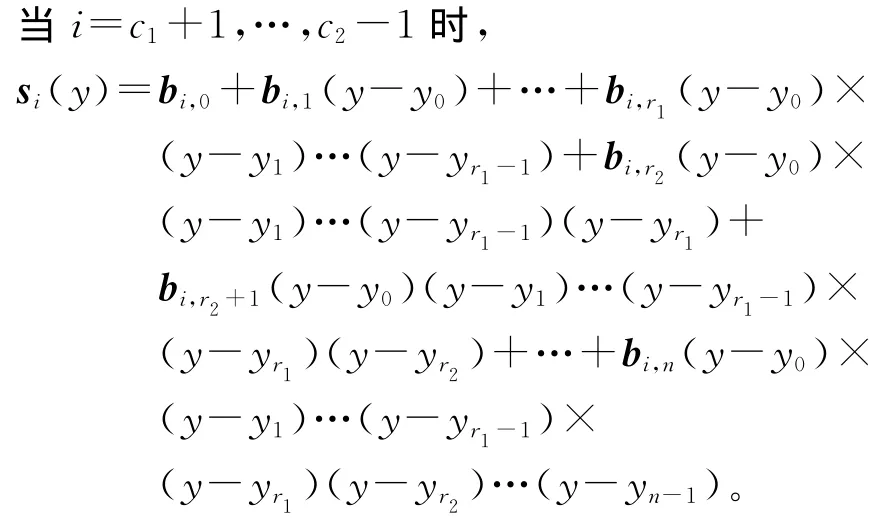
图1 Π的结构示意图

1.2 算法的实现

算法步骤［8］为：

（1）对于（i，j）∈｛（k，l）｜k＝0，1，…，m；l＝0，1，…，n｝－｛（k，l）｜k＝c1＋1，…，c2－1；l＝r1＋1，…，r2－1｝，令

（2）对于j＝0，1，…，r1，r2，…，n；p＝1，2，…，c2－1；i＝p，…，c2－1及j＝r1＋1，…，r2－1；p＝1，2，…，c1；i＝p，…，c1，令

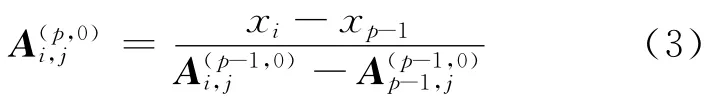
（3）对于i＝0，1，…，c1；q＝1，2，…，n；j＝q，…，n及i＝c1＋1，…，c2－1；q＝1，2，…，r1，r2，…，n；j＝q，…，r1，r2，…，n，令

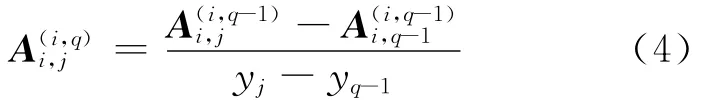
其中，当q＝r2时，令（4）式中的q－1取r1。

（4）当i＝c1＋1，…，c2－1；q＝r1＋1，…，r2－1时，计算

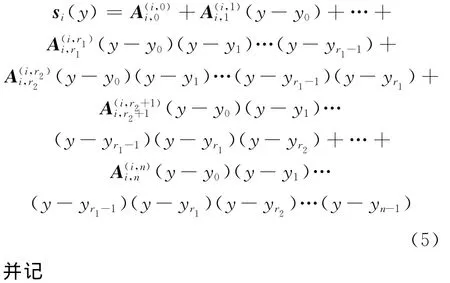
（5）当i＝c2，…，m；p＝1，2，…，i；j＝0，1，…，n时，计算（3）式。

（6）当i＝c2，…，m；q＝1，2，…，n；j＝q，…，n时，计算（4）式。

（7）由（1）式，当i＝0，1，…，c1，c2，…，m时，有

当i＝c1＋1，…，c2－1时，si（y）按（5）式计算。

1.3 奇异点的消除

在构造向量值有理插值函数时，可能产生奇异点，本文采用文献［9］的方法来解决，即根据插值节点的分布状况，通过调节插值节点的顺序，采用向量值混合有理插值的方法消除奇异点。

2 模块的划分

图像数据具有区域性，可以在分析图像数据局部特征的基础上，将图像数据划分为不同的区域模块，依据各模块的统计特征，分别采用不同的插值方法进行插值处理，以便提高图像插值的速度和效果。插值模块如图2所示。

图2中，B为要修复的部分，周围＊部分为像素已知区域。令vij＝（rij，gij，bij）表示第i行、第j列的像素，rij为红色分量，gij为绿色分量，bij为蓝色分量。

图2 插值模块

根据不同模块的特征，将图像模块分为平坦模块、边缘模块和纹理模块3类。

2.1 平坦模块

设¯r、¯g、¯b分别表示已知像素的红色、绿色和蓝色分量的平均值，ε为给定的域值，M为模块的像素平均向量值，即

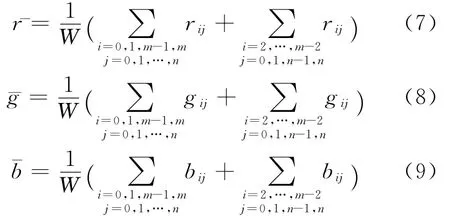
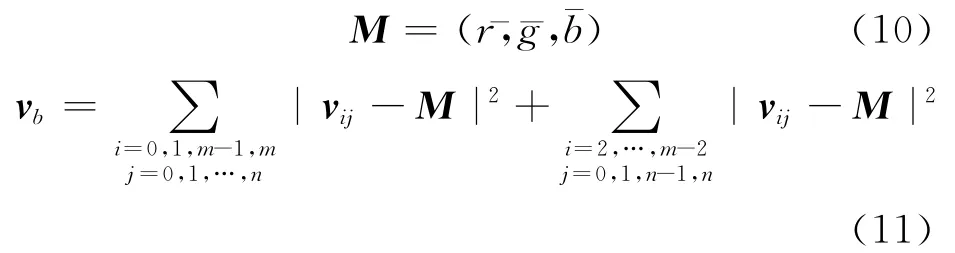
其中，｜·｜表示取模；W＝4m＋4n－8。

若vb＜ε，则像素块定义为平坦模块。

2.2 边缘模块与纹理模块

对于图像模块中的每个像素，对其位置进行标记，即

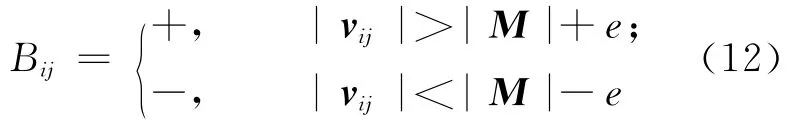
其中，i＝0，1，m－1，m；j＝0，1，n－1，n；Bij表示图像模块中的（xi，yj）位置处像素的标记；｜·｜表示取模；e为一个小的正数。

模块的划分情况如图3所示。

图3 模块的划分

如果图像的模块出现了如图3所示的4种情况，则认为该模块是边缘模块。

既不具备平坦模块特征，又不具备边缘模块特征的模块定义为纹理模块。

3 利用混合缺向量值有理插值修复图像

（1）对要修复的小区域，用矩形块去遮盖（块的大小不能超过4×4），如图2中的B。

（2）将矩形方块向外扩2个像素。如果扩充的像素为未知信息，则运用一元混合向量有理插值方法填充外扩的像素。

（3）根据上面模块的划分将图像进行分类，针对不同特征的模块采取不同的插值方法构造相应的向量值插值函数。平坦模块采取Newton－Newton型缺向量值插值形式，纹理模块采取缺向量值的Thiele－Thiele型向量值有理插值形式。而边缘模块采用沿边缘方向的缺向量值Newton－Thiele型或Thiele－Newton型混合向量值有理插值形式。

（4）对上述混合向量值有理插值曲面进行采样，然后进行修复。

4 图像质量的评估与实验结果

峰值信噪比（Peak Signal to Noise Ratio，简称PSNR）是评鉴画质的客观量测法。2个m×n单色图像I和K，如果I为原始图像，K为破损后修复的图像，则其均方差定义为：

峰值信噪比为：

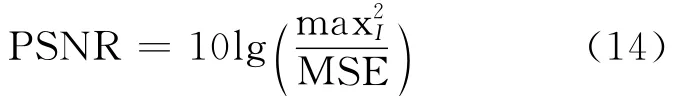
其中，maxI为表示图像点颜色的最大数值，如果每个采样点用8位表示，那么就是255。更为通用的表示是，如果每个采样点用B位线性脉冲编码调制表示，那么maxI就是2B－1。

对于每点有R、G、B 3个值的彩色图像来说，峰值信噪比的定义类似。

本文相关实验均在Windows XP系统下完成的，机型为Intel酷睿双核、CPU 为 T6670、2.2GHz主频、2G内存和320G的硬盘。为了验证本文方法的有效性，本文在破损程度低的情况下进行图像修复，并且对比了本文算法与TV算法、CDD算法的性能。本文主要从时间和PSNR上对3种算法进行了对比，结果见表1所列，如图4、图5所示。

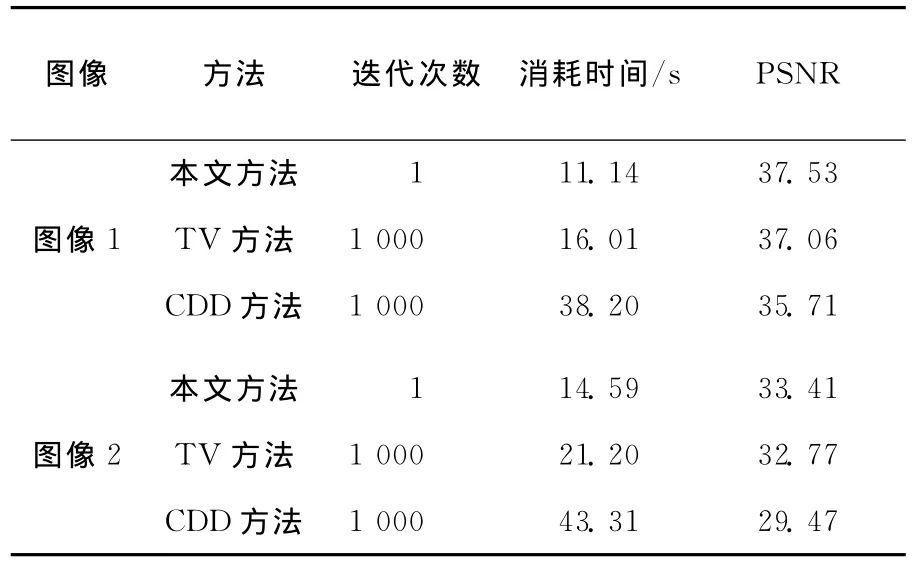
表1 3种算法的比较

从图4、图5及表1可以看出，本文算法的修复结果比TV方法和CDD的效果要好，时间更短。

图4 3种方法对图像1进行迭代修复的比较

图5 3种方法对图像2进行迭代修复的比较

5 结束语

目前的彩色图像修复多是对R、G、B颜色分量分别进行处理，割裂了3个分量之间的关系，从而使修复的图像产生一定程度的失真。本文应用二元混合缺向量值有理插值的方法，将R、G、B 3个颜色分量作为一个向量整体进行处理，使修复效果更好。

［1］Bertalmio M，Sapiro G，Caselles V，et al.Image inpainting［C］／／Proceedings of International Conference on Computer Graphics and Interactive Techniques，New Orleans，Louisiata，USA，2000：417－424.

［2］Chan T F，Shen J H.Mathematical models for local nontexture inpaintings［J］.SIAM Journal on Applied Mathematical，2002，62（3）：1019－1043.

［3］Chan T F，Shen J H.Non－texture inpainting by curvaturedriven diffusions［J］.Visual Communication and Image Representation，2001，12（4）：436－449.

［4］苏本跃，盛 敏.自适应图像缩放的切触有理混合插值算法［J］.计算机工程与应用，2010，46（1）：196－199.

［5］胡 敏，张佑生.Newton－Thiele插值方法在图像放大中的应用研究［J］.计算机辅助设计与图形学学报，2003，15（8）：1004－1007.

［6］胡 敏，檀结庆.基于Thiele型向量连分式插值的彩色图像放大方法［J］.合肥工业大学学报：自然科学版，2003，26（6）：1137－1140.

［7］胡 敏，檀结庆.保持轮廓清晰的有理－线性彩色图像内插放大方法［J］.系统仿真学报，2004，16（12）：2857－2863.

［8］檀结庆，朱晓临，唐 烁，等.连分式理论及其应用［M］.北京：科学出版社，2007：247－269.

［9］Zhu Xiaolin，Zhu Gongqin.A Study of the existence of vector valued rational interpolation［J］.Journal of Information＆ Computational Science，2005，1168（1）：631－640.

Image inpainting based on blending bivariate lacunary vector－valued rational interpolants

HU Da－hai， ZHU Xiao－lin
（School of Mathematics，Hefei University of Technology，Hefei 230009，China）

A method of color image inpainting based on the bivariate lacunary vector－valued rational interpolants is presented.In this method，each pixel of the digital image is viewed as a vector of R，G，B values defined on a planar domain，and Newton－Newton，Newton－Thiele，Thiele－Newton，or Thiele－Thiele vector－valued interpolants are applied to constructing a vector－valued interpolation surface according to the variation trend of the known pixels，and then the damaged areas are restored based on the sampling of the interpolation surface.Experimental results show that this algorithm is more efficient and less time consumption than TV method and CDD method.

bivariate lacunary vector－valued rational interpolant；blending vector－valued continued fraction interpolant；color image inpainting

O173.2

A

1003－5060（2012）11－1577－05

10.3969／j.issn.1003－5060.2012.11.032

2012－03－19；

2012－05－14

教育部科学技术研究重大资助项目（309017）；第38批留学回国人员科研启动基金资助项目（2010JYLH0322）；安徽省自然科学基金资助项目（11040606M06）和国家大学生创新性实验计划资助项目（101035937）

胡大海（1988－），男，安徽亳州人，合肥工业大学本科生；

朱晓临（1964－），男，安徽池洲人，博士，合肥工业大学教授，硕士生导师.

（责任编辑 闫杏丽）