基于半平面上的不重叠Schwarz交替法

刘红梅， 王寿城

（合肥工业大学 数学学院，安徽 合肥 230009）

基于半平面上的不重叠Schwarz交替法

刘红梅， 王寿城

（合肥工业大学 数学学院，安徽 合肥 230009）

文章讨论了基于半平面上自然边界归化的无界区域上不重叠Schwarz交替法及其离散化，对于区域的分解方法是将无界的半平面分解为不重叠的2个区域，即很小的有界区域和无界的半平面，并且在有界区域和无界区域上分别交替利用有限元法和自然边界元法求解，对于其中离散情形的不重叠型区域，分解算法利用极值原理证明其在最大模意义下的几何收敛性。

不重叠Schwarz交替法；半平面；自然边界元；离散化；极值原理；几何收敛

0 引 言

文献［1－4］给出了有界区域的不重叠Schwarz交替法，基于自然边界归化处理无界区域问题的理论，本文将不重叠Schwarz交替法推广到无界区域上，即将无界半平面Ω分解为一个很小的有界区域Ω1和一个无界区域Ω2，在Ω1上可用标准有限元方程，而在Ω2上则可直接通过自然边界归化得到的Poisson积分公式。

本文考虑Possion方程的外边界问题，即

其中，Ω为适当光滑的曲线Γ0下方的无界区域，Γ0＝Γ01∪Γ02，Γ01为在上半平面中的简单开曲线段，且的左右端点A和B在x轴上，Γ02＝｛（x，y）｜y＝0｝／，如图1所示。

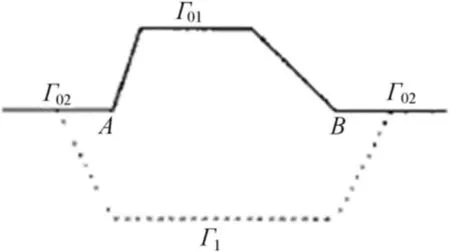
图1 无界区域及其分解Ω＝Ω1∪Ω2

对于问题（1），本文给出连续情形的不重叠Schwarz算法和离散情形的不重叠Schwarz算法，并在线性元的情况下利用离散极值原理证明离散情形的几何收敛性。

1 算法及其离散化

不妨在Γ01下方作简单曲线Γ1，使得Γ0和Γ1所围的区域Ω1的边界∂Ω1适当光滑，记下半平面为Ω2，Γ2＝∂Ω1／Γ1。

对应（1）式的弱形式是求u∈H1（Ω），满足

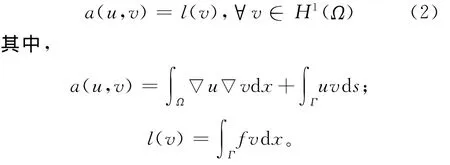
本文采用

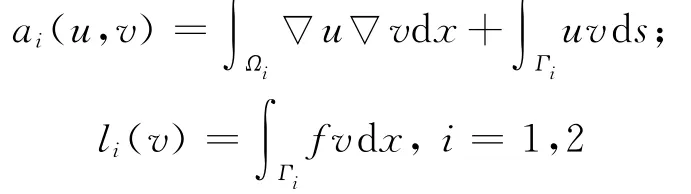
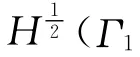
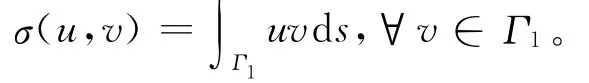
下面构造（1）式的解的迭代过程。

算法1 不重叠Schwarz交替法。其迭代步骤为：

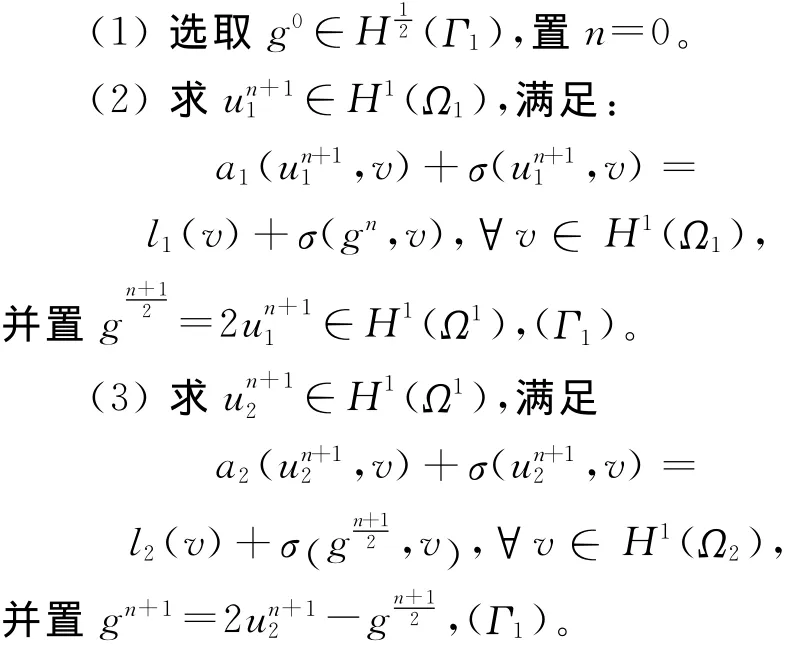
（4）置n＝n＋1，转步骤（2）。

算法1的有限元模拟为：首先对Ω1作正则三角形剖分（或四边形剖分），Pi（i＝1，2，…，N）为内结点，Pi（i＝N＋1，N＋2，…，N＋M）为边界结点，即Ω1h上的线性元空间为Sh（Ω1h），用Γ1h表示剖分在Γ1上的分划，Γ2h表示剖分在Γ2上的分划，Φh表示Sh（Ω1h）在Γ1上的迹空间［5－6］。

（1）式的有限元近似为求uh∈Sh（Ω1h），满足a（uh，v）＝l（v），∀v∈Sh（Ω1h）。

下面对算法1进行离散模拟。

算法2 离散不重叠Schwarz交替法。其迭代步骤为：

（1）选取初始g0∈Φh，置n＝0。

（2）求∈Sh（Ω1h），满足：

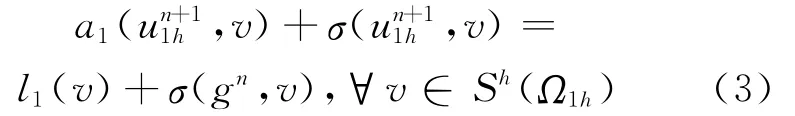
并置

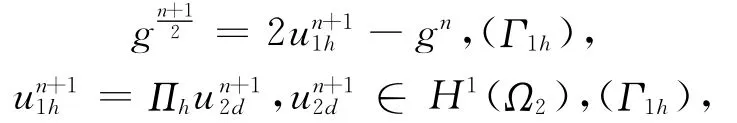
其中，Πh：C（Γ1）→Sh（Ω1h）上的插值算子。

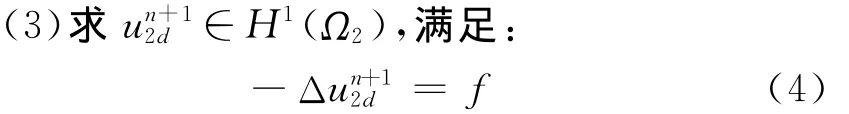
（4）转步骤（2）。

对于离散的不重叠Schwarz算法中的（3）式在Sh（Ω1h）上利用有限元求解，（4）式在下半平面利用Poisson积分公式求解［7］，即

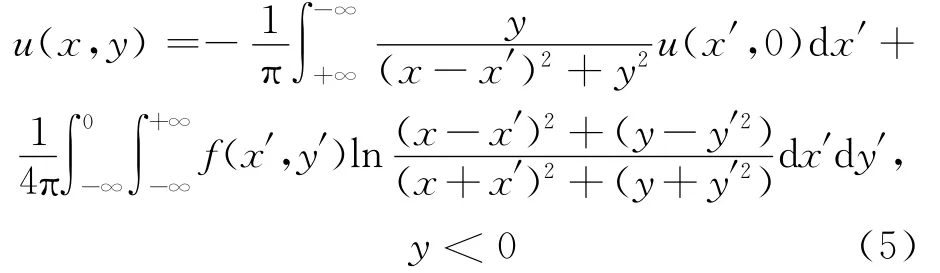
2 离散情形的几何收敛性

从而离散强极值原理成立［8－9］。

引理1 设ωh∈Sh（Ω1h），且满足：

若令q0h＝sup｛ωh（x，y）｜（x，y）∈Ω1h｝，则0＜q0h＜1。

定理1 由（3）式和（4）式给定的序列｛｝和｛｝分别在Ω1h和Ω2上几何收敛，若分别设收敛解为uh和ud，则

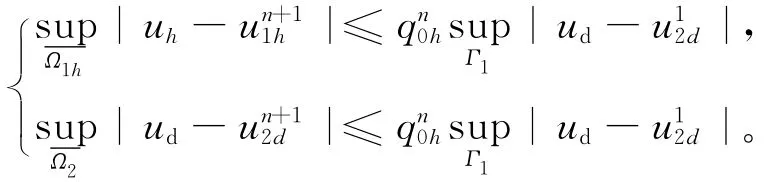
由（3）式和（4）式可得：

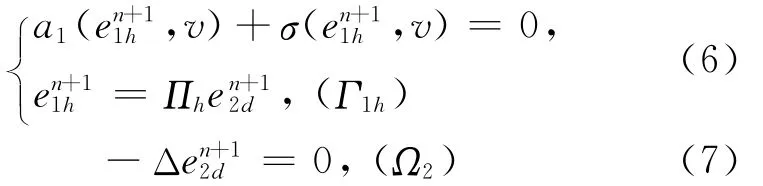
由（6）式和引理1得：

利用离散极值原理可得：

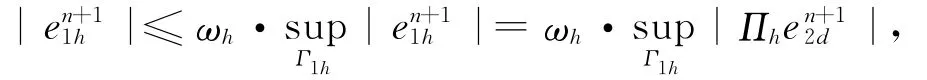
在Ω1h内，由引理1得：

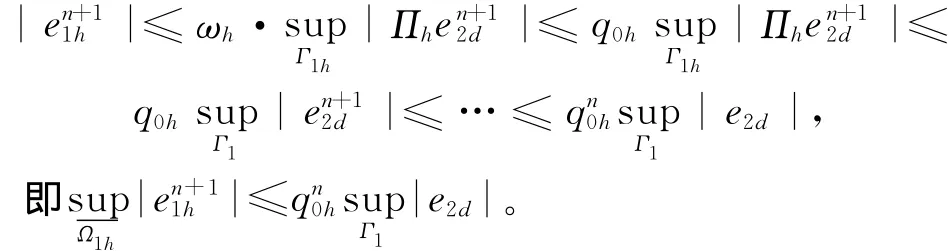
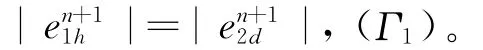
2d｜，定理1得证。

对于算法1的收敛性，可以通过算法2的收敛性及h→0的极限过程得到。

3 结束语

本文证明了无界区域的Schwarz迭代是几何收敛的，且离散情形的算法在有界区域和无界区域是不对称的，在有界区域上可用标准有限元方程求解，而在无界区域上则可直接应用Poisson积分公式直接求解。

［1］吕 涛，石济民，林振宝.区域分解算法：偏微分方程数值解新技术［M］.北京：科学出版社，1992：227－231.

［2］余德浩.无界区域上基于自然边界归化的区域分解算法［J］.计算数学，1994，16（4）：448－459.

［3］余德浩.无界区域非重叠区域分解算法的离散化及其收敛性［J］.计算数学，1996，18（3）：328－336.

［4］蒋美群，邓庆平.一个双调和方程的Schwarz交替法［J］.计算数学，1994，16（1）：93－101.

［5］余德浩.自然边界元方法的数学理论［M］.北京：科学出版社，1993：71－103.

［6］数学手册编写组.数学手册［M］.北京：高等教育出版社，1979：559－593.

［7］郑 权.余德浩.基于半平面上自然边界归化的无界区域上的Schwarz交替法及其离散化［J］.计算数学，1997，19（2）：205－218.

［8］Ciarlet P G，Raviart P A.Maximum principle and uniform convergence for the finite element method［J］.Comput Methods Appl Mech Engrg，1973，2：17－31.

［9］Wang Leiheng.On the max－min principle for the linear finite element equation for the Dirichlet problem of Laplace equation［C］／／Proc of China－France Symp on FEM.Beijing：Science Press，1983：1019－1026.

An underlapping Schwarz alternating method over half－plane

LIU Hong－mei， WANG Shou－cheng
（School of Mathematics，Hefei University of Technology，Hefei 230009，China）

In this paper，an underlapping Schwarz alternating method of unbounded domains based on natural boundary reduction over half－plane and its discretization are discussed.The unbounded halfplane is decomposed into two underlapping domains，namely a bounded domain and an unbounded domain，and the finite element method and natural boundary element method are used in these two domains respectively for their solutions.And the geometric convergence of the underlapping Schwarz alternating method in discrete problem under the maximum module is shown by the extremum principle.

underlapping Schwarz alternating method；half－plane；natural boundary element；discretization；extremum principle；geometric convergence

O241.82

A

1003－5060（2012）11－1582－03

10.3969／j.issn.1003－5060.2012.11.033

2012－03－16

刘红梅（1987－），女，安徽六安人，合肥工业大学硕士生；

王寿城（1956－），男，安徽寿县人，合肥工业大学副教授，硕士生导师.

（责任编辑 闫杏丽）