基于决策偏好距离的多阶段群决策快速集结方法

卢志平， 陆成裕

（1.合肥工业大学 管理学院，安徽 合肥 230009；2.广西工学院 管理系，广西 柳州 450006）

基于决策偏好距离的多阶段群决策快速集结方法

卢志平1，2， 陆成裕2

（1.合肥工业大学 管理学院，安徽 合肥 230009；2.广西工学院 管理系，广西 柳州 450006）

针对具有互反判断矩阵偏好信息的多阶段群决策问题，文章提出了一种基于决策偏好距离的快速集结方法。首先对决策偏好距离相关概念进行定义，阐述了基于决策偏好距离的多阶段群决策集结过程；其次，利用决策偏好距离算法对单一专家的阶段内权重和阶段间权重进行测度，得出最优的专家权重；然后，通过加权几何平均算子拟合出最优的专家判断矩阵和最优的群体决策偏好；最后，给出算例，分析结果表明该方法具有合理性。

群体决策；多阶段群决策；决策偏好距离；专家阶段权重

由于具有个体决策所不具有的优势，群体决策已成为社会生活中很重要的决策方式。目前群体决策的相关研究成果主要集中在群体决策环境分析［1－2］、决策问题分解与集结［3－5］、群体偏好集结［6－8］和群体决策支持系统设计［9－10］等方面。群体决策过程之所以采用多阶段的形式，其目的在于使决策专家之间多多沟通与交互，充分共享决策知识，以获取高质量的决策结果。因此，在群体决策问题研究上，如何实现多阶段、交互式的决策过程，快速、高效地集结群体的决策意见，属于该研究领域的热点问题。文献［11］针对传统群决策中全局反馈方式的不足，提出了一种阶段反馈式群决策模型，并通过群成员间多阶段的交互和启发，产生满足群体期望要求的群体满意解，从二元语义的角度探讨了决策专家间相对评价一致性问题。文献［12］考虑到决策信息集结过程中存在信息的疏密程度，提出一种基于密度算子的信息集结方法，对多阶段群体评价数据从横向与纵向进行集结。文献［13］研究了群决策过程中决策者基于多个决策阶段、多种结构形式的判断偏好集结方法，利用决策者判断偏好的一致性水平和与群体综合偏好偏差的距离，提出了确定决策者权重的方法。文献［14］对多轮群体决策问题进行研究，讨论利用多轮偏好信息获取决策者满意偏好的具体方法。上述文献均从多阶段的角度对群体决策过程中决策专家的决策偏好集结进行分析与研究，文献［11］仅考虑到群体决策过程的信息反馈交互问题，通过迭代的方式获取群体最优集结评价结果，未考虑到决策专家的权重。文献［12，14］仅研究了多阶段群体决策中不同阶段间专家意见的直接集结方法，未考虑到单一专家的阶段间权重差异问题。而文献［13］对不同阶段间的群体决策权重问题展开了分析，通过先验信息和方案区分度进行阶段赋权，具有较好的现实意义，但是未考虑到单一专家的阶段间权重问题，同时偏好集结算法过于复杂，不便于快速地集结决策者的决策偏好。

在上述文献的基础上，本文针对现实生活中一类具有互反判断矩阵偏好信息的多阶段群决策问题，提出一种基于决策偏好距离的集结算法，采用简单而且常用的加权平均算子对阶段内的专家权重和单一专家的阶段间权重进行测度，快速地拟合出群体最优决策偏好，充分体现出群体决策的优势。

1 相关理论基础

1.1 满意一致性矩阵

［15］，有定义1。

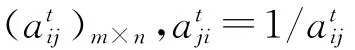
1.2 决策偏好距离

（1）决策满意偏好。

定义2 设某一决策专家对某一多属性决策问题进行决策。在每个决策中均给出一个决策方案间两两对比的判断矩阵At＝（）m×n，其中t表示第t个决策阶段，t＝1，2，…，T。假定判断矩阵At具有满意一致性，则称w为决策满意偏好，而且有：

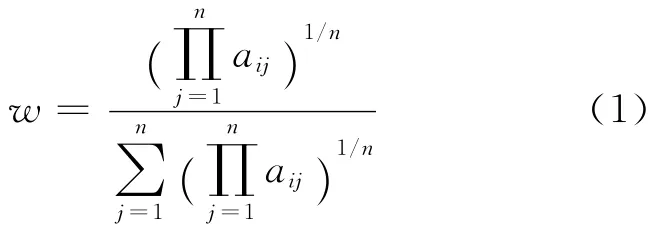
决策满意偏好包括了单一决策阶段内的群体满意偏好和多个决策阶段的专家满意偏好。群体满意偏好可以通过决策过程的横向决策偏好集结而得，专家满意偏好可以通过决策过程的纵向决策偏好集结而得。

（2）决策偏好距离。

定义3 假设存在2个决策偏好向量为X＝（x1，x2，…，xm）T和Y＝（y1，y2，…，yn）T，其中m，n∈N，m＝n，则称D为2个决策偏好的距离，而且有：

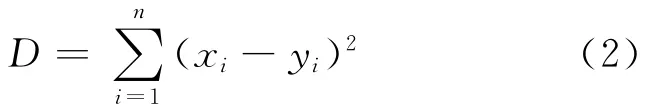
（3）专家阶段权重。

定义4 假设第t个决策阶段内，若决策偏好向量X为某一专家偏好向量，Y为某相关满意偏好向量（包括横向的群体满意偏好和纵向的专家满意偏好），D为X与Y的偏好距离，则称为专家阶段权重（包括横向的专家阶段内权重和纵向的专家阶段间权重），而且有：

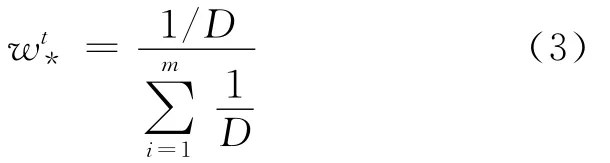
2 基于决策偏好距离的群体决策集结

2.1 问题描述

某一个多阶段多属性群决策问题，设m个决策专家G＝｛d1，d2，…，dm｝对n个备选方案P＝｛p1，p2，…，pn｝进行T个阶段的多次交互决策。决策专家在每个阶段均给出一个决策方案相对比较的判断矩阵＝（）m×n。其中，t＝1，2，…，T；k＝1，2，…，m。根据以上信息进行决策计算。

2.2 单一专家的阶段内权重测度

通过计算单一专家的阶段内偏好与阶段内群体偏好之间的距离大小来确定专家的阶段内权重。计算思路为：首先采用几何平均法对每个阶段的专家判断矩阵进行计算，得到单一专家的阶段内偏好；然后计算阶段内的群体偏好；最后计算单一专家阶段内偏好与群体偏好的距离，并得出专家的阶段内权重。具体计算过程如下。

（1）采用几何平均算子计算阶段内专家偏好。利用（1）式对阶段内的专家判断矩阵At＝）m×n进行计算，得出阶段内的专家偏好。

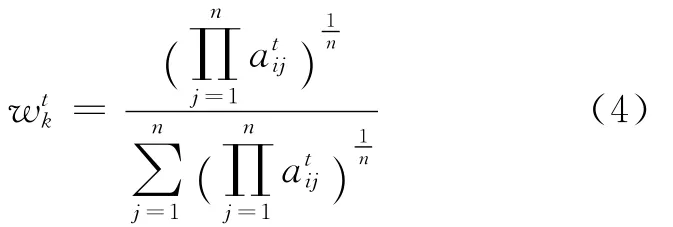
（2）采用几何平均算子WGA计算阶段内群体偏好。由步骤（1）得到的专家偏好构成一组偏好矩阵Ht＝（）m×n，利用（1）式计算阶段内群偏好。

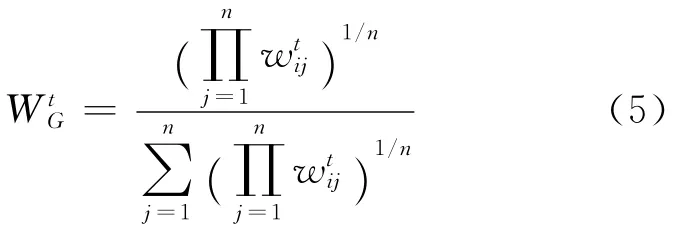
（3）根据（2）式计算阶段内的专家偏好与本阶段群体偏好之间的偏好距离，并结合（3）式得出本阶段内的专家权重。

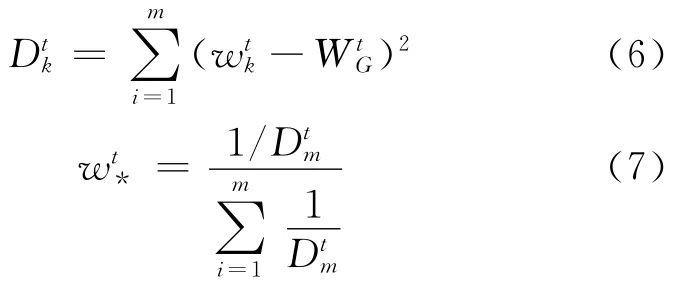
2.3 单一专家的阶段间权重测度

通过计算阶段之间单一专家偏好的距离大小来确定专家的阶段之间权重。计算思路为：首先采用几何平均算子对单一专家的每阶段判断矩阵进行计算，得出每阶段的单一专家偏好；然后采用几何平均算子计算出多阶段的专家满意偏好；最后根据偏好距离法计算出每阶段专家偏好与专家满意偏好的偏好距离，并计算单一专家的阶段之间专家权重。具体计算过程如下。

（1）采用类似于阶段内的专家偏好计算办法生成多阶段单一专家的专家偏好。利用（1）式对由每阶段的单一专家判断矩阵＝（）m×n进行计算，得出每阶段的单一专家偏好。

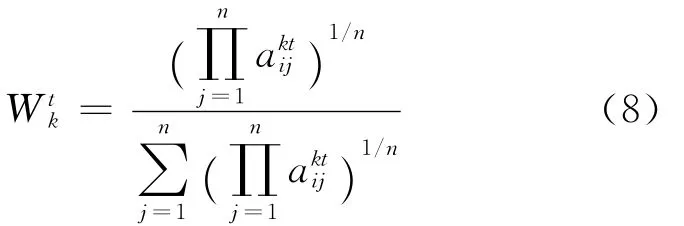
（2）将单一专家在每个阶段的偏好构成偏好矩阵Hk＝（）m×n，利用几何平均算子计算出单一专家的满意偏好Wk。

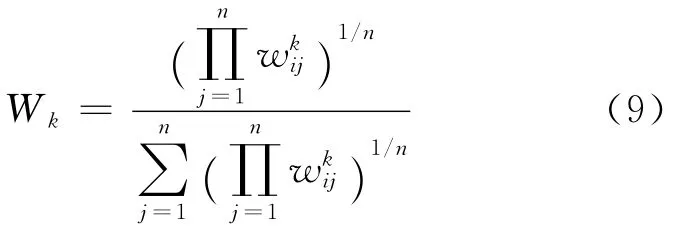
（3）根据偏好距离法计算出每阶段专家偏好与该阶段专家满意偏好的偏好距离Dk，并计算出阶段间的单一专家权重。

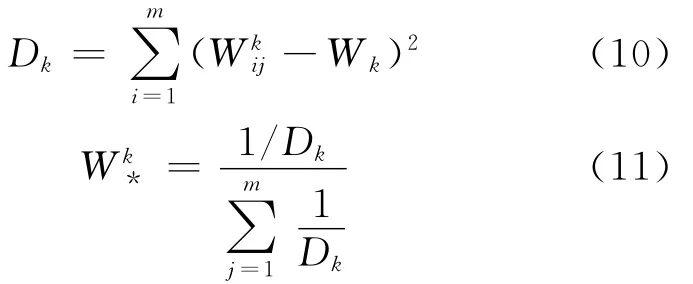
2.4 最优专家权重拟合

首先根据上述得到的阶段内专家权重，组成多阶段权重矩阵＝（）m×n。然后结合阶段之间的单一专家权重，采用加权几何平均算子拟合出专家权重W＊，归一化后即得专家的综合权重V＊。

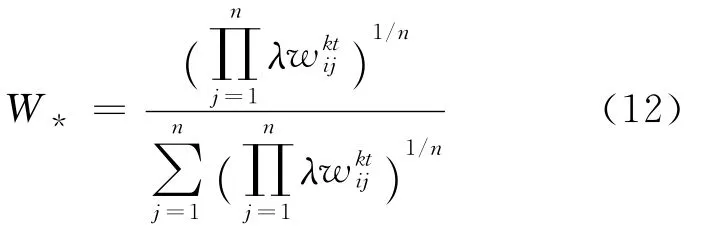
其中，λ为阶段之间的单一专家权重，由确定。

2.5 最优专家判断矩阵拟合

根据计算出的阶段间专家权重，采用加权几何平均法拟合出专家的最优判断矩阵＝（）m×n。

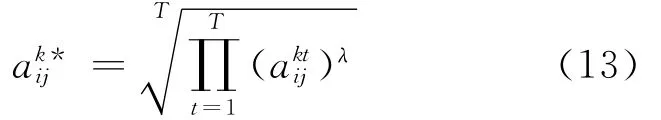
2.6 最优群体偏好拟合

根据最优的专家拟合判断矩阵＝（）m×n，采用加权几何平均算子拟合出最优的群体满意判断矩阵B＝（bij）m×n，再采用几何平均算子计算出最优群体偏好W＊。

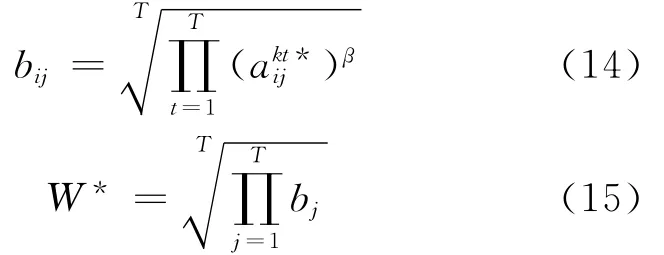
其中，β为最优专家权重，由V＊确定。

3 算 例

某单位为了选拔某部门的中层干部，组成了由3位专家构成的考核评价小组，对4位候选人的能力水平进行3个阶段考核评价，以选出综合能力最优的候选人。决策专家集为G＝｛d1，d2，d3｝，备选方案集为P＝｛p1，p2，p3，p4｝，T＝3。每轮考核的专家评价数据［14］，即每位专家对各个方案进行两两比较得出的互反判断数据如下。

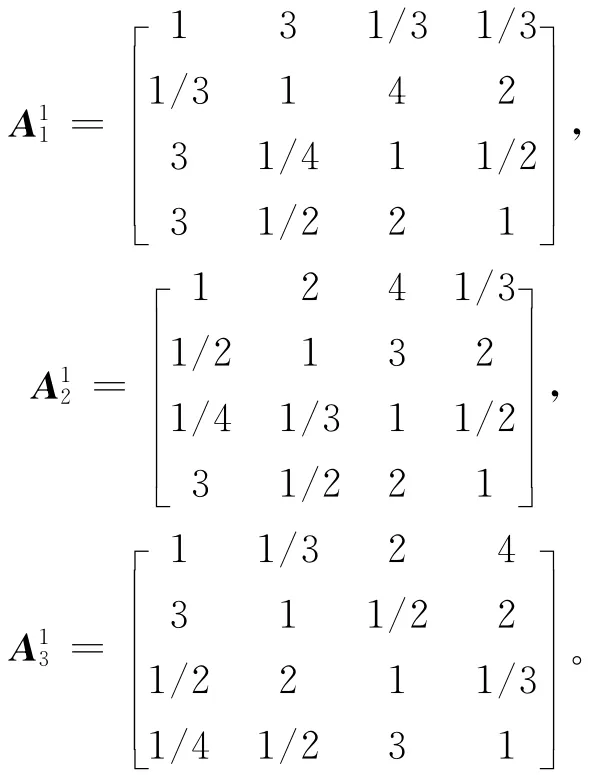
第1阶段的专家互反判断矩阵为A、。

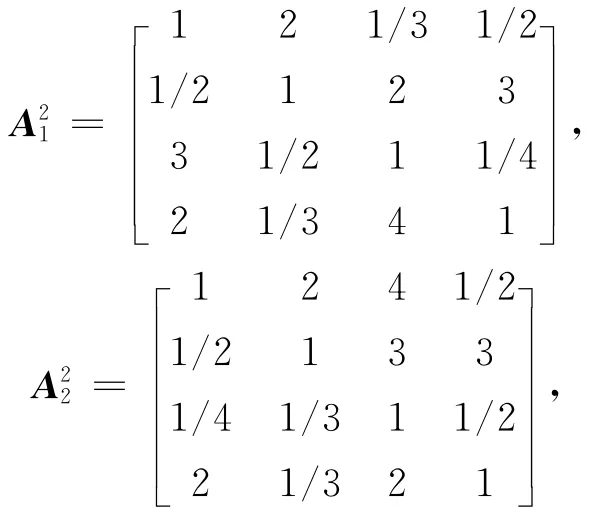
第2阶段的专家互反判断矩阵为。

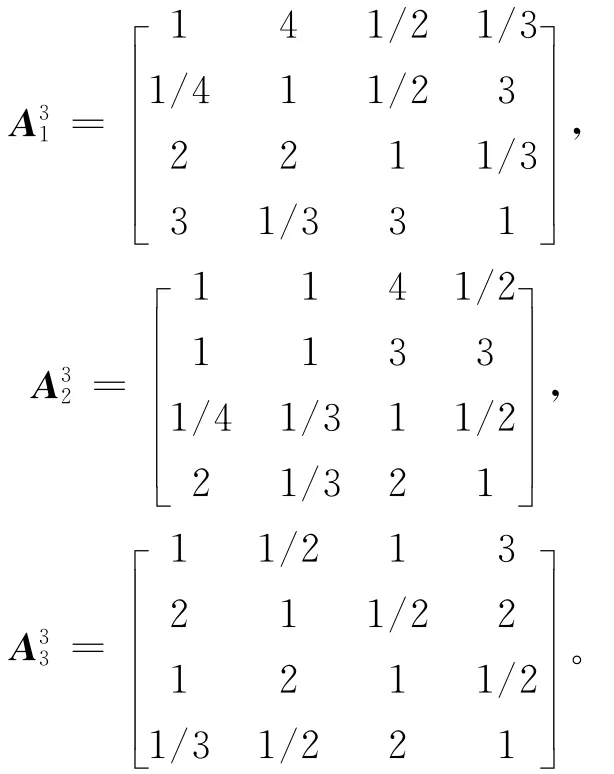
第3阶段的专家互反判断矩阵为。

具体计算过程如下：

（1）对每个阶段内评价过程的专家偏好、专家权重以及群偏好进行计算。利用（4）～（7）式可得数据，见表1所列。

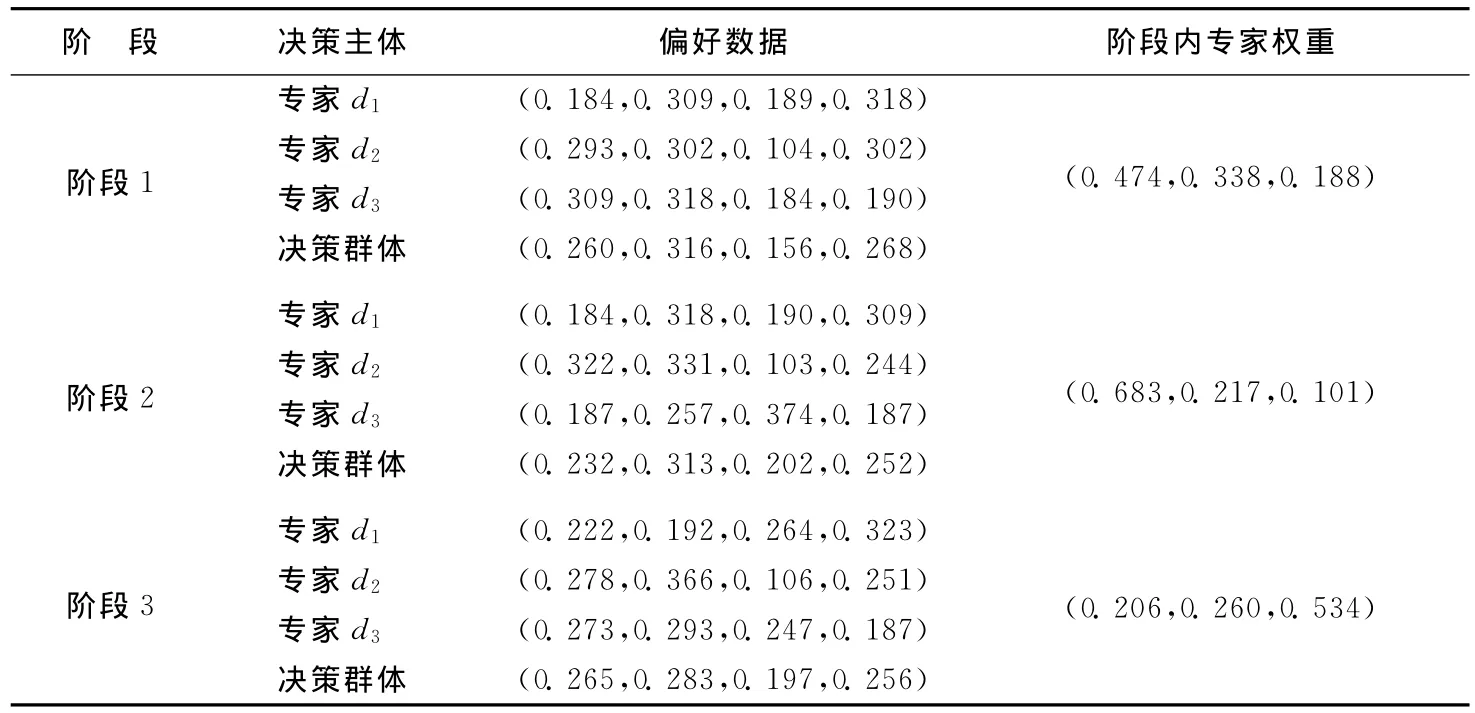
表1 阶段内数据计算结果

（2）对前后阶段之间单一专家的阶段权重和单一的专家满意偏好Wk进行计算。利用（8）～（11）式可得数据，见表2所列。

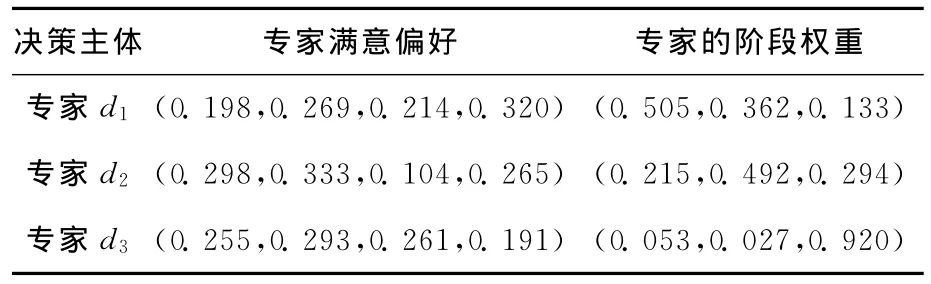
表2 阶段间数据计算结果

（3）利用（12）式对专家的阶段权重进行拟合并进行归一化，得到最优专家权重V＊，即

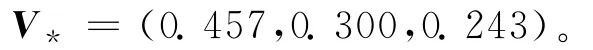
（4）利用（13）式对专家判断矩阵进行拟合，得到最优专家判断矩阵。

（5）利用（14）式对最优专家判断矩阵进行拟合，得出最优群体判断矩阵B＝（bij）m×n，并利用（15）式拟合出最优群体偏好W＊。

由此可得3位候选人的综合能力评价排序为：p2≻p4≻p1≻p3，即第2位中层干部候选人为最优选择结果。

可见，该决策偏好集结结果与文献［14］的决策结果一致，均选择第2位候选人为最优结果。虽然文献［14］的偏好集结算法亦较为简洁，但由于未考虑到多阶段群体决策过程中单一专家阶段之间的权重，未能充分地体现出决策信息的交互性、共享性以及专家权重差异性。相比之下，本文所提出的决策偏好快速集结方法没有涉及太复杂的算法，能考虑到单一专家的阶段权重问题，因此更具有合理性和现实意义。

4 结束语

多阶段交互式的群体决策问题主要体现在阶段之间的决策者偏好集结研究上。针对一类以互反判断矩阵为决策信息多阶段群体决策问题，本文提出了一种基于决策偏好距离的快速集结方法。首先，对满意一致性矩阵、决策满意偏好、决策偏好距离以及专家阶段权重等概念进行定义。然后，详细分析了阶段内的专家权重和单一专家的阶段间权重的测度方法，得出最优专家权重。最后，拟合出最优专家判断矩阵和最优群体偏好。算例分析结果表明，本文提出的决策偏好快速集结模型简单易行，且更具有合理性。

［参 考 文 献］

［1］Surowiecki J.The wisdom of crowds［M］.Anchor，2005：27－33.

［2］高 波，费 奇，陈学广.面向分布式决策环境的主体结构模型［J］.科技进步与对策，2008，25（10）：135－139.

［3］张志强，张朋柱.面向复杂决策任务的综合集成决策研讨总体 框 架 设 计 ［J］.系 统 工 程 理 论 与 实 践，2006，1（1）：9－17.

［4］于长锐，罗 艳，徐福缘.复杂决策问题的多元化模型体系研究［J］.管理科学学报，2004，7（2）：88－94.

［5］于长锐，徐福缘，向 阳.复杂决策问题形式化方法研究［J］.管理科学学报，2002，5（6）：9－16.

［6］郑文婷，刘红美，余 真.多阶段群体满意决策最优算法［J］.数学的实践与认识，2008，38（16）：44－48.

［7］和媛媛，周德群，王 强.基于模糊判断矩阵的群决策方法研究［J］.中国管理科学，2008，16（2）：128－131.

［8］梁昌勇，戚筱雯，张 鑫.一种基于不同粒度且属性权重未知的群决策方法［J］.运筹与管理，2010，19（1）：43－48.

［9］徐振宁，张维明.基于 MAS的群决策支持系统研究［J］.管理科学学报，2002，5（1）：85－92.

［10］徐选华，陈晓红.复杂大群体决策支持系统结构及实现技术研究［J］.计算机工程与应用，2009，45（13）：16－19，41.

［11］金 伟，付 超.基于二元语义和T－OWA算子的阶段反馈式群决策模型［J］.合肥工业大学学报：自然科学版，2009，32（6）：851－856.

［12］张发明，郭亚军，易平涛.基于密度算子的多阶段群体评价信息集结方法及其应用［J］.控制与决策，2010，25（7）：993－997.

［13］朱建军，刘思峰，李洪伟，等.群决策中多阶段多元判断偏好的 集 结 方 法 研 究 ［J］.控 制 与 决 策，2008，23（7）：730－734.

［14］彭 怡.动态群体决策理论及其应用研究［D］.成都：西南交通大学，2006.

［15］樊治平，姜艳萍.语言判断矩阵满意一致性的判定方法［J］.控制与决策，2004，19（8）：903－906.

Quick preference aggregated method for multi－stage group decision－making based on decision preference distance

LU Zhi－ping1，2， LU Cheng－yu2
（1.School of Management，Hefei University of Technology，Hefei 230009，China；2.Dept.of Management，Guangxi University of Technology，Liuzhou 450006，China）

In order to solve the multi－stage group decision－making problems of preference information in the form of reciprocal judgment matrix，this paper proposes a quick aggregated model based on decision preference distance.Firstly，the related concepts of the decision preference distance are defined，and the whole process of multi－stage group decision－making based on decision preference distance is stated.Then，based on the decision preference distance algorithm，a single expert’s weight of in－stage and between－stage can be measured to gain the optimized expert’s weight.Thirdly，the optimized judgment matrix of experts and the optimized decision－making preference of groups are computed out by weighted geometric averaging operator.Finally，an analytical example proves that the decision preference distance model is very effective.

group decision－making；multi－stage group decision－making；decision preference distance；stage weight of experts

C934

A

1003－5060（2012）03－0398－05

10.3969／j.issn.1003－5060.2012.03.025

2011－07－07；

2012－01－04

国家自然科学基金资助项目（90718037）；高等学校博士学科点专项科研基金资助项目（200803590007）

卢志平（1977－），男，瑶族，广西来宾人，合肥工业大学博士生，广西工学院副教授.

（责任编辑 张淑艳））