非良基公理的本质及其应用

姚从军

（湖南科技学院思政部，湖南 永州 425100）

一、图、装饰及精确图

埃泽尔（Aczel）方法的基本思想是使用有向图描述集合。一个图由一个结点集和一个边集组成，每一条边都是一个由结点组成的序对＜n，n′＞。如果＜n，n′＞是一条边，那么我们写成 n→n′。一条路径是一个由＜n0，n1＞，＜n1，n2＞，……连接的有穷或无穷序列 n0→n1→n2…；一个点图是带一可区分结点的图，这一可区分结点称为该图的始点；一个点图是可达的仅当对于每个结点n都有一个从该图的始点n0到结点n的路径n0→n1→…→n。对于图G的一个已知结点n，n的后继集用nG表示，即如果n→n′，那么n′∈nG。对于一个结点n，如果nG=φ，我们称n为死结点。如果从结点n0到结点nk之间存在一条路径，我们就称nk是从n0可通达的[1]3～4。我们用NG表示可达点图G的结点集。

如果一个可达点图的装饰把集合x指派给它的始点，我们称该可达点图是集合x的图像；如果该装饰把不同的集合指派给它的不同结点，我们称这个可达点图是集合x的一个精确图。

例如，图1左图就是序数3的精确图，右图是它的非精确图。

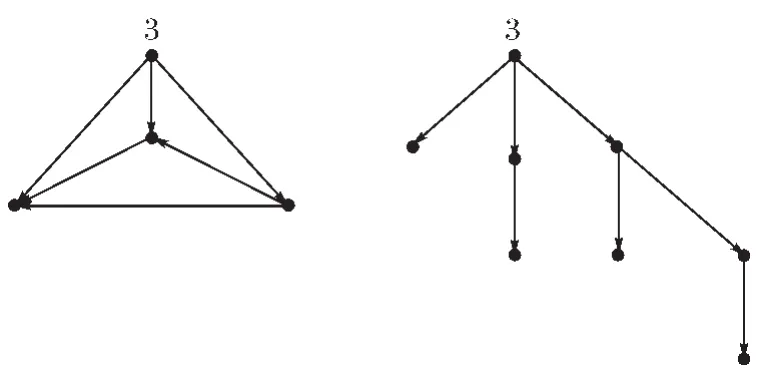
（图1）序数3的图像

不计同构（把同构的对象看作同一个对象），每个集合的精确图是唯一的。因此，如果我们知道哪个图是精确图，那么我们就知道存在什么样的集合，确定存在什么样的集合，必须先确定什么样的图是精确图。如何确定精确图呢？在良基背景下，我们通过外延性来确定精确图：一个良基图G是精确图当且仅当G是外延的。那么由该精确图类确定的良基的集合类Vwf={G|G∈V0∧G是良基的∧G是外延的}（这里的“=”不是真正意义上的相等，可以理解成这样的一种对应性：右边的每个可达点图唯一地对应于Vwf中的某个集合，Vwf的每个集合的精确图都是右边的元素，此处V0是可达点图集），这就决定了良基集合的域。在非良基背景下，如何确定精确图呢？

二、精确图与非良基公理

（一）外延性与BA1（BAFA的弱形式）

首先，应该除去非外延的图，非外延的图存在两个不同结点有相同的后继集，如图2：

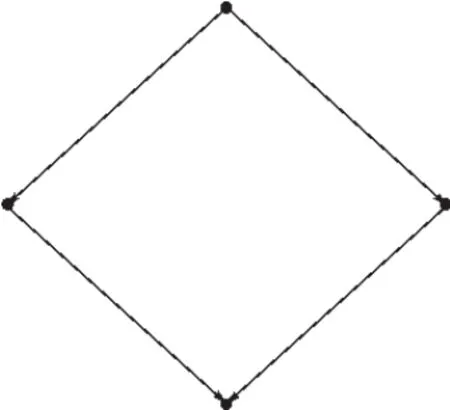
（图2）一个非外延的可达点图

中间的两个结点都只有一个后继，即底端的结点，因此这两个结点一定被指派相同的装饰集合（实际上是{Ø}），该可达点图不是一个精确图。如果只用外延性来刻画精确图，就得到布法（Boffa）的一个弱的反基础公理BA1：一个可达点图是精确图当且仅当它是外延的[2]。并因此形成相应的反良基集合的域B={G∈V0|G是外延的}。把BA1加在系统ZFC-就构成了一个非良基公理系统，考虑图3：

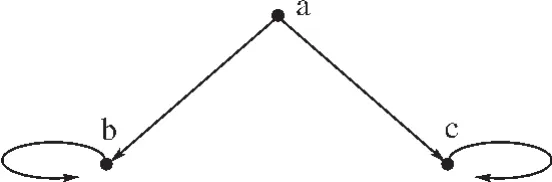
（图3）一个Boffa集合的精确图

这是一个外延的可达点图，并且是满足A={B，C}、B={B}、C={C}的一个集合A的图像，B和C相等吗？这里外延公理失去效用，因为它仅仅告诉我们B=C当且仅当B=C。在反基础公理BA1的假设下，自反集B={B}和C={C}是互不相同的集合。事实上，可以证明，在BA1中像x={x}这样的自反集有无穷多个，图3是上面所描述的集合A的精确图，这里B≠C。然而从直觉上看B应该和C相等，为了刻画这种思想，需要比外延性公理更强的公理。问题是，这个公理是什么？

（二）外延的且严格的与YAFA

可以用另一个方式来解释图3作为意欲的精确图是有问题的，即说它是非严格的（non-rigid）。如果一个图具有非恒等映射作为自身的同构映射，那么这样的同构也叫真自同构，这样的图被称为非严格的图。而图3有一个使b和c互相映射的真自同构，根据它们在图中的作用，这两点不该区分开来，并因此应该用相同的集合来装饰它们。因此，在寻找精确图的时候，要排除非严格图。注意严格性也不蕴涵外延性（见图5），因此仅用严格性来确定精确图也是外延公理不允许的。但是可把二者合起来形成新的反良基公理YAFA：一个可达点图是精确图当且仅当它是外延的且严格的；并因此形成了相应的反良基集合的域Y={G∈V0｜G是外延的且严格的}；把YAFA加入ZFC-中就可以形成新的非良基集合论。这样形成的精确图还是不太合理，考虑图4：

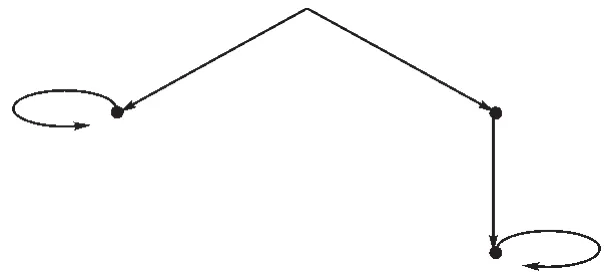
（图4）一个严格的但不是同构外延的可达点图

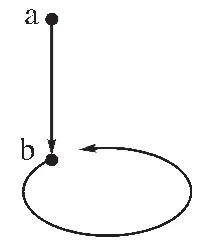
（图5）一个同构外延的但非外延的可达点图

这是严格的且外延的图。底端的每个结点被一个等于自己的单元素集所装饰，装饰这两个结点的集合似乎应该相等，需要更严格的精确图概念。

随着中国城镇住房金融制度的改革，改革开放40年中，住房金融市场逐步衍生、发展和繁荣。纵观改革开放40年，我们不难发现，中国城镇住房金融对开发商获得土地、商品房开发、商品房购买和消费提供了金融支持。

（三）芬斯勒外延的与FAFA

一个合适的性质是同构外延性。已知一个图G和G的一个结点a，我们可以形成可达点图Ga如下：Ga的结点和边是G中从a点出发的那些路径上的结点和边，其中a是Ga的始点。对任意的结点a，b∈G，如果Ga≌Gb，那么a=b，我们就说G是同构外延的。

同构外延的意味着：在一个同构外延的图里面，绝不可能存在不同的结点a和b使得以a为始点的子图同构于以b为始点的子图。明显同构外延性蕴涵严格性，但同构外延性也不蕴涵外延性，如图5。

所以仅用同构外延性来确定精确图也是外延公理不允许的。可以说一个可达点图是精确图当且仅当它是外延的和同构外延的，这就是反基础公理FAFA。此公理还有一种等价的表述：“一个可达点图是精确图当且仅当它是芬斯勒外延的”。这就形成了芬斯勒集合的域F={G∈V0|G是外延的且同构外延的}，把FAFA加在ZFC-上就形成了芬斯勒非良基集合论[3]683～173。

（四）斯科特外延的与SAFA

已知一个可达点图，如果从它的始点到它的所有结点的路径是唯一的，我们就称该可达点图是一棵树图。树本身也是一种可达点图。一个可达点图的展开把可达点图的从始点开始的有穷路径作为结点，把形如（a0→…→a，a0→…→a→a′）路径有序对作为边，把长度为1的路径a0作为始点。因此，展开总是一棵树。可以用一种明显的方式从一个原始可达点图的装饰诱导出它的展开图的装饰，也就是指派给树的结点a0→…→a的集合就是通过原始可达点图的装饰指派给结点a的集合。图1中序数3的精确图（左图）被展开成3的树图（右图）。

一棵树是严格的（或非冗余的）仅当该树不存在真自同构。令Ga是一个可达点图，可以证明：如果它的展开（Ga）t是严格的，那么Ga是同构外延的和外延的。Ga是斯科特外延的当且仅当对该图的任意结点 b，c，（Gb）t≌（Gc）t蕴涵 b=c[4]。如果 Ga是斯科特外延的，那么（Ga）t是严格的，所以斯科特外延的蕴涵同构外延的和外延的。斯科特反良基公理SAFA可陈述为“一个可达点图是精确图当且仅当它是斯科特外延的”，这就形成了斯科特集合的域S={G∈V0|G是斯科特外延的}，把SAFA加到ZFC-得到斯科特非良基集合论。为显示SAFA和FAFA的差异，考虑图6：

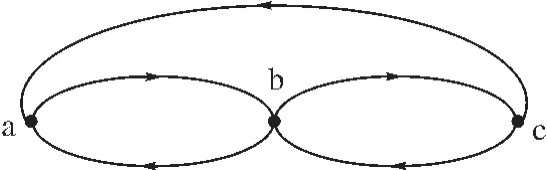
（图6）芬斯勒外延图

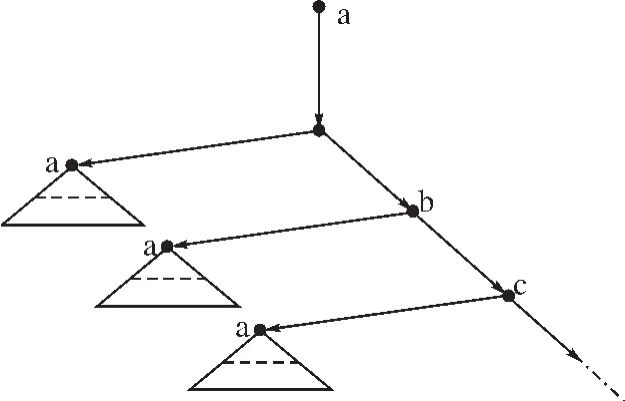
（图7）Ga的展开图（Ga）t

既然所有的结点之间彼此可通达，此图可被看作始点为a，b，或c的图。易证此图是外延的和同构外延的，根据 FAFA，它是满足 A={B}，B={A，C}和 C={A，B}的三个不同集合 A、B、C 的精确图；但是，以 b和c为始点的两个可达点图的展开（Gb）t和（Gc）t是同构树（见图7），公理SAFA强迫b=c，故它不是SAFA下的精确图。

（五）强外延的与AFA

对于任意一个可达点图Ga，Ga的任意结点b和c来说，如果b和c具有互模拟关系，那么b=c，我们就说Ga是强外延的。最后，我们看看受到广泛关注的非良基集合论——AFA集合论。AFA公理被描述为：一个图是精确图当且仅当它是强外延的。埃泽尔本人将该公理表示为“每个可达点图是唯一集合的图像”，或者“每个图都有唯一装饰”。这些描述都是等价的。这样就可以得到埃泽尔非良基集合的域A={G∈V0|G是强外延的}。把AFA加到ZFC-就得到埃泽尔非良基集合论。

再看看图6。存在一个把Ω={Ω}指派给每个结点的装饰；根据AFA这个装饰是唯一的。因此在AFA的域中，既没有FAFA允许的不同的集合A、B、C，也没有SAFA允许的不同的集合A、B。a、b、c三点都具有互模拟关系，所以图6不是强外延的。这些公理给出了递降的集合论域：B⊇Y⊇F⊇S⊇A。

三、FAFA或AFA

尽管FAFA断定的是最自然的非良基集合论系统，但是事实上AFA在近几年最引人注目。是什么理论在支持AFA呢？埃泽尔自己几乎没有给予讨论，但他在《非良基集合论》中给出了莫斯托夫斯基（Mostowski）坍塌引理：每个良基图有一个唯一装饰。这里的唯一性明显是为了导出在AFA下相对应的唯一性。但是，莫斯托夫斯基坍塌引理中的唯一性根源何在呢？准确地说，良基性允许我们递归地定义唯一装饰。在非良基情况下，唯一性需要一个不同的论证。但是，埃泽尔没有提供。

支持AFA的另一来源是巴威斯和莫斯的《恶性循环》，但在这里，支持AFA的理由同样是简单的。他们考虑了满足d={q，d}的集合d的数量（可把q看作某个固定的集合）。

假定d1和d2都是这个方程的解，那么无限地展开这些集合，我们看到：di={q，{q，{q，…}}}。

这里i=1、2。直观上说，没有什么东西可以把这两个集合区分开来。沿着此路线展开下去，它们都是相同的。除字母之外，承认任意差别都会违反外延公理的精神，外延公理的精神实质是说“集合由它的元素完全确定”。于是巴威斯和莫斯断言仅仅存在一个这样的d，并且那个装饰总是唯一的。

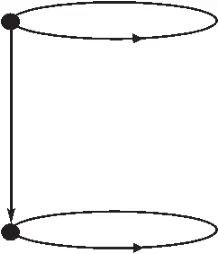
（图8）Ω＊的一个图像

需要指出两点，一是这个论证几乎能够支持“同构的集合是相等的”原则，FAFA是这一原则的形式化版本，但是它不能支持更强的原则：集合只要有可能就相等；二是连d1、d2是否同构也不是很清楚。假设d1=q，d2≠q，那么d1只有一个元素，d2有两个元素。为明白这一点，取q=Ω。因此我们正在寻找方程d={Ω，d}的解。这个解是图8中那个顶点的可能装饰。

一个解d=Ω。另一个可能的解d=Ω*，这里Ω*≠Ω，Ω*={Ω，Ω*}。尽管Ω和Ω*都满足：

d={Ω，{Ω，{Ω，…}}}。

但是Ω和Ω*不同构。当然，在AFA的域中，不存在Ω*，因为图8的唯一装饰把Ω指派给每一个结点。但是巴威斯和莫斯在证明AFA（每个图有唯一装饰）成立时假定了方程解的唯一性，而现在证明这个方程有唯一解时又假定AFA成立，这就给人有乞题之嫌。

所有这些似乎相当抽象，现在看看在一个相对具体的背景下FAFA与其他公理有什么不同。迄今为止，众所周知的对非良基集合的应用是巴威斯和莫斯提出的用来解释说谎者悖论，这里只需要他们的基本理论。在这个理论中，命题可以用一个n-元组描述。例如，“巴黎是浪漫的”可以用一个有序对来描述p=＜ro，pa＞，这里ro和pa是原子。关于其他命题的命题，还需要表示真和假的原子。因此命题断定“命题p 是真的”可以模型化为＜tr，p＞。

当允许自我指谓时，悖论就出现了。因此，一个断定自己假的说谎者命题p1被模型化为p1=＜fa，p1＞。如果把有序对模型化为集合的话，如＜x，y＞={{x}，{x，y}}，那么p1一定是非良基的。巴威斯和埃切门第（Etchemendy）使用的非良基集合论实际上是带有原子的AFA集合论。这个集合论把有互模拟关系的集合看作是同一集合（而FAFA仅仅把同构的集合看作同一集合），巴威斯和埃切门第被迫把具有互模拟关系的不同结构的命题看作是同一命题。沿着图8的思路，我们给出一个例子。首先可能尝试给出两个命题：

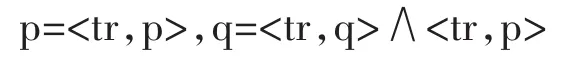
一个包含合取式，另一个没有，这两个命题在理论上就是不同的，我们把它们修改成：

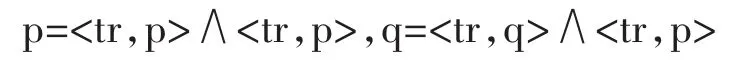
AFA强迫p=q。存在一个唯一的p满足第一个方程，并且埃泽尔1988年给出的及巴威斯、埃切门第1987年给出的解引理也保证了这两个方程形成的方程组的唯一解的存在性[5]241～253（这个引理等价于AFA，它断言“任意这样的方程组有唯一解”）。很明显，一个解可通过允许p=q获得，因此，这就是唯一解。然而直观上，p和q应该有不同的结构，并因此应该表达不同的命题，实际上，直观上可以有p为真q为假。

在非良基集合的应用中，解引理是很方便的。当我们能够使用ZF的归纳定义的时候，解引理保证了这些定义仍然是唯一的，但是这个唯一性以丧失域的丰富性为代价。如果能够证明与FAFA相对应的某个解引理版本，运用FAFA会更容易达到我们的目标。一个可能的方法是证明在众多的解中，总存在一个具有特定性质的唯一解。这些应该得到进一步研究。显然，如果接受所有的非良基集合，那么应该接受的不仅仅是AFA域中的东西。

[1] Peter Aczel.Non-Well-Founded Sets[D].Stanford：CSLI Publications，1988.

[2] M.Boffa.Forcing et negation de 1’axiom de fondement[J].Memoire Acad，Sci.Belg.XL，1972，（7）.

[3] P.Finsler.Uber die Grundlagen der Mengenlehre[J].I.Math Zeitschrift，1972，（25）.

[4] D.Scott.A different kind of model of set theory[C].unpublished paper presented at the 1960 Standford Congress of Logic，Methodology and Philosophy of Science.

[5] Adam Rieger.An Argument for Finsler-Aczel Set Theory[J].Mind，2000，109（434）.