自适应波束形成算法工程应用中的关键技术研究

徐 伟

(西安电子工程研究所 西安 710100)

1 引言

自适应波束形成技术是阵列天线系统中一项有效的抗干扰措施，可广泛应用于雷达、通信、声纳等领域。目前数字波束形成技术在阵列天线系统中已有了大量的应用。然而从数字波束形成到自适应数字波束形成的大量应用还有差距。自适应数字波束形成工程应用遇到的主要问题是算法实现所需资源与性能之间的矛盾。算法实现所需资源主要包括硬件运算量和存储量。算法的性能主要包括稳健性、收敛速度和收敛精度。其中运算量和稳健性是自适应数字波束形成能否工程应用的关键问题。一般来说，运算量小的算法稳健性较差，稳健性好的算法运算量又较大。于是作为自适应数字波束形成技术的特例，自适应旁瓣对消技术得到了广泛的应用。

经典的自适应波束形成算法以最大信噪比为准则计算最优波束形成权值。全自适应算法运用所有可能的自由度来抑制干扰和噪声，导致算法运算量较大，收敛速度慢，所需快拍数量大。为减少运算量，可采用部分自适应算法。部分自适应算法可分为两大类:降维处理和降秩处理。降维处理先做物理上的确知变换，再做自适应处理，如子阵方法和子波束方法。降秩处理先构造降秩矩阵或增加约束，再做自适应处理，如特征干扰相消器、直接主分量法、正交投影法和GSC框架主分量法。随着大规模集成电路的发展，数字电路系统的运算处理能力有了很大的提高，但同时阵元数量也在成倍增加，自适应算法要求的运算量与数字电路系统处理能力之间的矛盾依然存在。将自适应算法与现场可编程逻辑阵列(FPGA)器件相结合，是提高自适应算法实时性的一条途径。由于目前基于FPGA的矩阵运算处理程序还不完备，所以还有大量工作要做。

在自适应算法工程应用中，由于实际系统本身存在误差，如通道幅相误差、位置误差、频率特性失配、阵元互偶，以及外部环境，如多径引起的信号扩散、相干，都会影响自适应算法性能下降甚至失效。此外还有信号的工作带宽、有限采样数据长度、干扰估计数据中存在有用信号、数据运算处理精度等因素也会影响自适应算法的稳健性。为提高算法的稳健性可采用部分自适应、对角加载、线性约束等方法。稳健的波束形成算法也有适用条件，如基于特征子空间的算法在低信噪比环境下性能下降［1］。

对于单脉冲雷达而言，在信号检测同时需要测量到达角度。这就不仅要关心波束形成器输出信噪比，同时还要保持主瓣形状，以保持测角精度。基于以上原因目前主要考虑了自适应旁瓣对消算法的工程实现。

2 稳健的自适应算法概述

最具代表性的稳健自适应算法是线性约束最小方差(LCMV)波束形成算法。其基本思想是增加一系列的线性约束，以增加主瓣的宽度，控制零点的位置和宽度。这些约束条件可以是信号导向矢量，也可以是信号导向矢量的高介导数。线性约束最小方差算法描述如下:

其中w为最优化的权矢量，R为阵列接收数据的自相关矩阵，C为N×M维的约束矩阵，f为M×1维的约束值矢量。这里N为矩阵维数，M为约束条件个数。利用拉各朗日数乘法求解，得到最优化权值矢量:

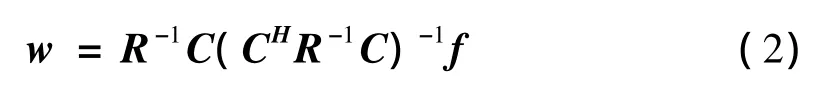
由此可见线性约束最小方差算法求解中需要矩阵求逆运算，算法稳健性会受R特征值分布影响。

为减少R特征值分布对算法稳健性的影响，通常采用对角加载的方法。对角加载波束形成算法描述如下:

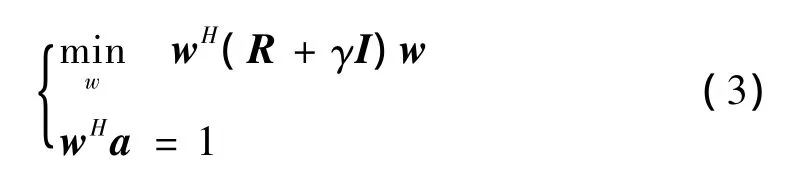
其中γ为加载量;a为信号导向矢量。对角加载算法通过加载量γ增加白噪声方差，提高对噪声的抑制，降低对干扰的抑制，从而提高算法稳健性。对角加载方法存在的主要问题是加载量的选取，目前的研究已经给出加载量为负值的近似解［1］。

基于特征空间(ESB)的自适应波束形成算法，描述如下:先分解阵列自相关矩阵，

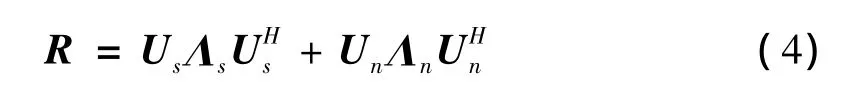
其中Us和Un分别为信号和噪声特征矢量矩阵，Λs和Λn分别为信号和噪声特征值对角矩阵，舍去其中噪声子空间对权值矢量的贡献，得到下式:

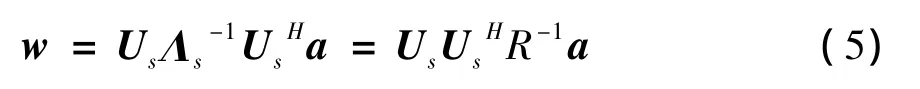
由此可见基于特征空间的算法也可看作是最小方差算法权值向信号加干扰子空间投影。基于特征空间的算法适用于有用信号较强的环境，能改善阵列数据包含有用信号带来的信号相消损失。当信噪比较低时，使得信号加快子空间估计不准，导致性能性能会恶化。

较新的自适应算法采用最差性能最优通用信号模型［2］，其最优化问题描述如下:

上式中建立了无数的约束条件，保证了在最差失配条件下的无失真响应。其中Δ1描述了自相关矩阵估计误差，Δ2描述了信号协方差矩阵估计误差，γ和ε为约束常数，分别限制了误差矩阵的范数。上式的解为矩阵(R+γI)-1(Rs-εI)的最大特征向量。

对比以上几种稳健的自适应波束形成算法可见，大多数采用了增加约束的策略提高算法稳健性。增加约束会增加运算量，给工程应用中算法实现带来困难，增加了系统所需硬件资源，降低了系统处理实时性，并且这些稳健的算法还需满足一定条件，在很大程度上限制了其工程应用。于是我们从减少运算量的思路出发，在部分自适应波束形成算法的基础上，采取一些提高稳健性的措施，使自适应波束形成算法即便于工程实现又具有较好的稳健性。

3 广义旁瓣对消结构的自适应算法

广义旁瓣对消器结构如图1所示。在k时刻，阵列接收数据矢量x(k)从上支路经过导向矢量a0加权得到主波束d0(k)，x(k)从下支路经过阻塞矩阵B0和自适应加权得到对消信号d0(k)，主波束减去对消信号得到对消结果y(k)。自适应权值计算公式为:

其中Rx0为阻塞矩阵处理后数据的自相关矩阵;rx0d0为阻塞矩阵处理后数据与主通道输出数据的互相关矢量。广义旁瓣对消结构与线性约束最小方差等价的权值为:

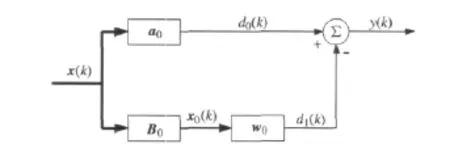
图1 广义旁瓣对消器结构

阻塞矩阵的选取是旁瓣对消技术的一个重点，关系到系统的性能和运算量。通常要求阻塞矩阵与主波束导向矢量正交，从而下支路不含期望信号，不会引起期望信号对消。构造阻塞矩阵有多种方法，如期望信号补空间、期望信号方向置零、辅助阵元、辅助波束等［3］。根据参考文献［4］结论，旁瓣对消系统的对消比上限取决于辅助通道的干噪比和辅助通道个数。同时为了降维处理方便，选择若干辅助波束构成阻塞矩阵，要求辅助波束指向干扰。由于辅助波束有一定宽度，因而对干扰方向估计精度要求不高，运算量不大。采用辅助波束相对于单个阵元，一个明显的好处是，能够较好的保持主通道波束形状。单个干扰在不同方向时，辅助阵元法和辅助波束法对比结果如图2和图3所示。

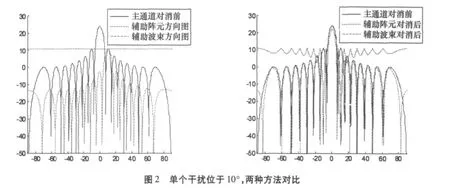
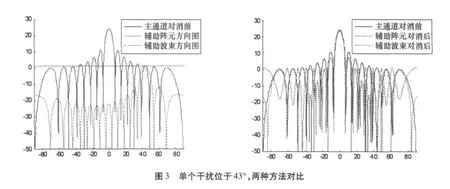
权值计算是旁瓣对消技术的另一个重点。根据权值计算表达式(7)，由于需要进行矩阵求逆处理，会影响算法的运算量和稳健性。当辅助波束数量增大时，系统自由度越大，可对消干扰数量越大，运算量越大。自适应权值的运算量随辅助波束数量会显著增加，尤其是矩阵求逆处理的运算量。硬件电路上可根据系统对权值更新速度的要求选用DSP或者FPGA器件来完成运算。DSP器件编程灵活但运算速度较慢，适合自适应权值更新速度要求不高的场合。FPGA器件运算速度高，但程序开发难度较大。算法的稳健性仍然受自相关矩阵特征值分布的影响，这里仍可采用对角加载方法来提高稳健性。

4 算法应用及试验结果

基于以上结构的广义旁瓣对消器已应用于某信号处理机。其中辅助通道采用辅助波束法，权值计算使用FPGA器件完成。为提高算法稳健性，先根据干扰侦察期间的天线接收数据判断有无干扰，确定是否开启自适应旁瓣对消。如果有干扰，再判断干扰的数量和方向，设置参与对消处理的辅助波束的数量和方向。根据干扰数据、主波束指向和辅助波束指向，旁瓣对消器计算权值并完成干扰对消。辅助波束数量较少时，权值计算可直接采用矩阵求逆公式。辅助波束数量较多时，宜采用矩阵分块、矩阵分解、线性变换等间接的方法进行矩阵求逆处理。为提高自适应权值更新的实时性，设计了基于FPGA的4维复数矩阵求逆处理软件单元，并可以方便的增加处理矩阵维数。

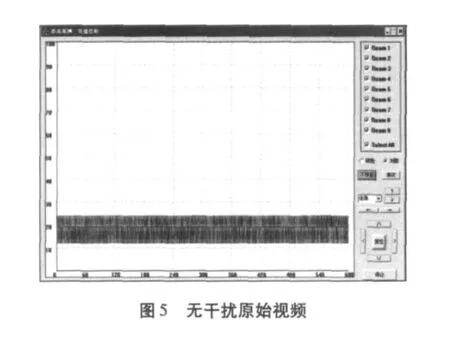
在外场环境中对一个干扰情况进行了实测试验。一个远场点频干扰经过阵列天线接收处理形成9个波束原始视频送给终端显示界面。测试方法为:固定9个主波束指向如图4所示，转动天线观察自适应开启和关闭时的原始视频输出。终端显示界面横轴表示距离，纵轴表示幅度，不同颜色代表不同波束，残留显示模式下多次原始视频同时显示。

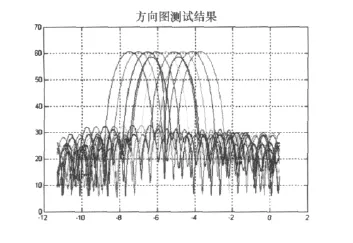
图4 主波束方向图

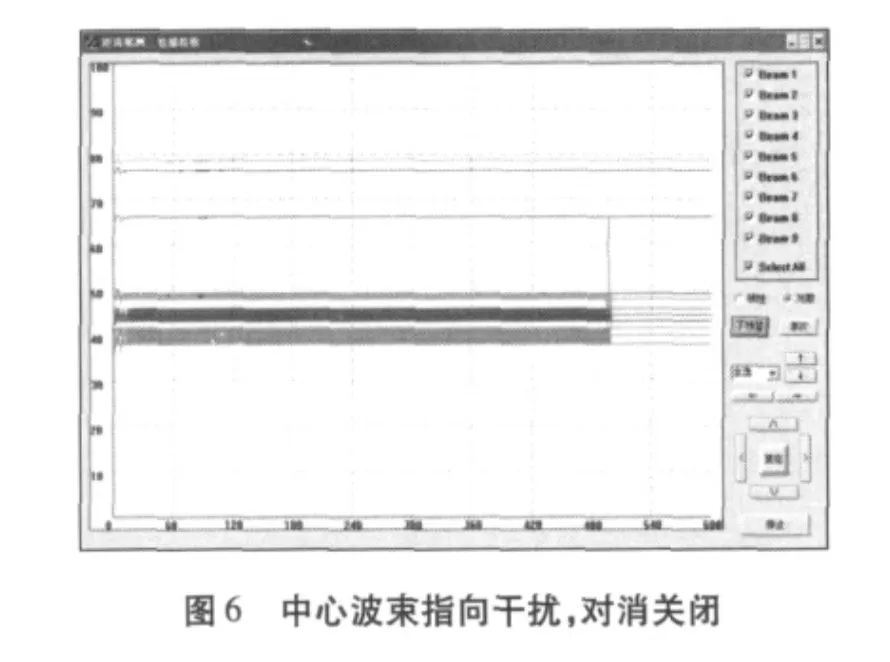
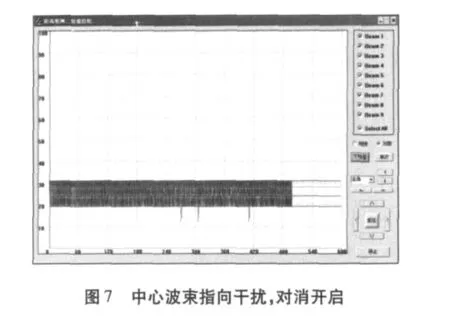
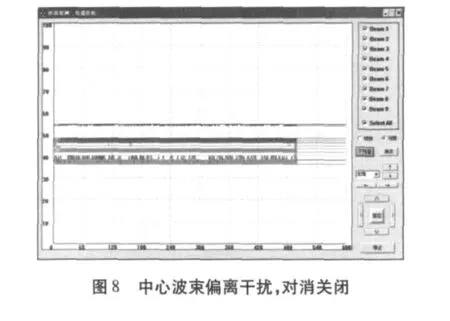
图5 为无干扰情况下的原始视频，输出噪声幅度小于25dB。图6和图7为中心波束指向干扰时的原始视频，对消前最大波束输出接近80dB，对消后所有波束输出小于35dB。图8和图9为中心波束偏离干扰5°指向时的原始视频，对消前最大波束输出接近55dB，对消后所有波束输出小于35dB。由图可见，对于单个干扰源，旁瓣对消算法有较好的稳健性。

5 结束语

本文在了解MIMO雷达发射正交信号的基础上，采用相位编码信号设计MIMO雷达的正交波形，通过分析其原理，构造目标函数，设计产生一组相位编码信号，再采用遗传算法对其进行优化，然后通过分析其自相关和互相关特性，并验证了这样设计的信号具有很好的正交性能。在设计产生正交相位编码信号的基础上，分析了信号码长、信号个数、信号的相位数对雷达性能的影响，这些在用相位编码信号设计MIMO雷达发射信号中都是必须考虑的问题，通过分析这些因素，为MIMO雷达在发射信号设计方面提供了一定的理论支持。

［1］强勇，张冠杰，李斌.MIMO雷达进展及其应用研究［J］.火控雷达技术，2010，39(1):1-10.

［2］Hai Deng，Polyphase Code Design for Orthogonal Netted Radar Systems［J］.IEEE Transaction on signal Processing，2004，52(11):3126-3135.

［3］张宇，王建新，孙锦涛，MIMO雷达的相位编码信号设计［J］.兵工学报，2010，31(1):109-112.

［4］吕红芬，宋万杰，张子敬等，基于遗传算法和贪心算法正交多相码设计［C］.第十一届全国雷达学术年会论文集，2010.11:377-381.

［5］李明，郝明，基于混合遗传算法的正交相位编码波形设计［J］.电子工程师，2007，33(10).

［6］陈金立.相位编码MIMO雷达信号处理技术研究［D］.南京理工大学博士论文，2010.

［7］刘波.MIMO雷达正交波形设计及信号处理研究［D］.电子科技大学博士论文，2008.

［8］雷英杰，张善文，李续武等.MATLAB遗传算法工具箱及应用［M］.西安:西安电子科技大学出版社，2004.