MIMO雷达目标检测问题研究

游 俊 强 勇 董 国 师志荣

(西安电子工程研究所 西安 710100)

1 引言

MIMO雷达是在系统中采用多个发射单元和多个接收单元的新体制雷达。与传统雷达不同，MIMO雷达系统的多个发射单元发射波形不同(理想情况正交)的信号，同时各接收单元接收多种波形，并通过分离获得多个通道数据，最后对这些通道数据进行融合处理，从而提高系统的检测能力。由于在接收端的信号分离，MIMO雷达系统能够形成远多于传统雷达系统的通道数，MIMO雷达的这种多通道获取数据的能力正是其根本优势所在。

由于系统采用多发多收的形式，当收发各单元之间间距足够大［1，2］时，雷达就能从多个不同角度对同一目标进行观察，而多个观测角度上获得的回波同时衰落的概率很小，从而降低了因目标散射系数随观察角度变化而剧烈变化对雷达检测性能的影响，MIMO雷达正是这样利用空间分集来改善目标RCS起伏特性的。

如果要形成完全的空间分集，MIMO雷达各收发单元之间必须有较大间距，这样就需要考虑各单元之间的排布以及各单元之间的通信同步等问题，加大了雷达的设计难度。同时形成空间分集后各接收信号之间相互独立的关系导致信号难以进行相干处理［3］，以空间分集增益换取相干处理增益是否值得，也是要是需要考虑的。

文献［4］基于目标的空间分布源模型研究了SwerlingⅠ模型在N-P准则下的最优检测——最大似然比检测，本文在此基础上从目标散射系数分布的角度研究了两大类SwerlingⅠ、Ⅲ模型的检测问题，并分析了其检测性能。

2 信号模型

假设MIMO雷达由M个发射单元和N个接收单元构成，各单元到空间中一点目标的距离分别为dTm，m=1，2，…，M 和 dRn，n=1，2，…，N，工作示意图如图1所示。

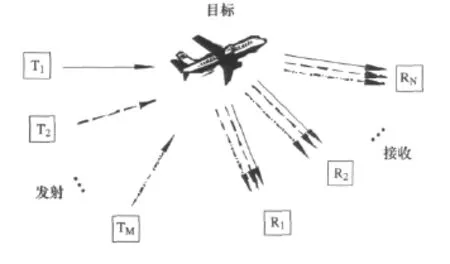
图1 MIMO雷达系统工作示意图

在不考虑多普勒频率以及杂波的影响下，接收单元Rn接收到的信号可以表示为:

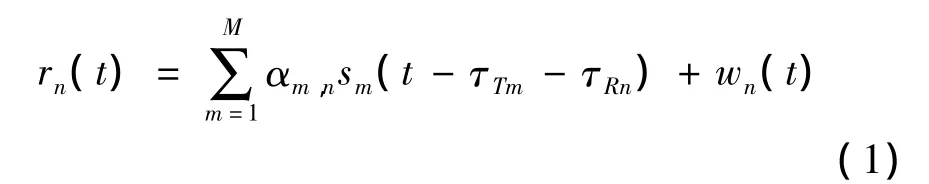
其中:αm，n表示电磁波从发射单元Tm经过目标到达接收单元Rn的传输系数，包括传输引起的信号幅度变化以及目标散射引起的相位变化;sm(t)表示发射单元Tm发射的信号;τTm、τRn分别表示信号从发射单元Tm到目标以及信号从目标散射到接收单元Rn的传输延时;wn(t)表示均值为0方差为的复高斯白噪声，且wn(t)(n=1，2，…，N)之间相互独立，这里假设各单元接收到的噪声能量相同，即=ο2，n=1，2，…，N。

根据雷达方程［5］如果用Pt表示总发射功率，对发射同载频信号的MIMO雷达系统，假设各发射单元天线增益为GtM、各接收单元天线增益为GrN，则

其中，σm，n表示从发射单元Tm经目标到接收单元Rn这一通道对应的目标RCS，φm，n表示通道对应的散射相位变化。

代入(1)，在距离得到补偿的前提下，最终简化得到

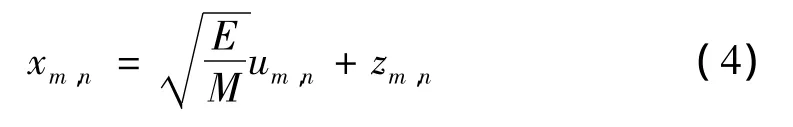
这里的xm，n表示回波信号与噪声电平的比，zm，n表示标准复高斯变量。

3 检测方法及性能分析

首先假定H1表示目标存在;H0表示目标不存在。似然比检测［6］为:

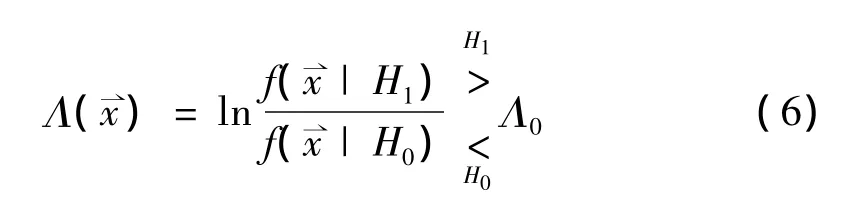
3.1 目标模型

由于雷达探测的目标复杂多样，很难准确得到目标散射系数的概率分布，这里主要根据常用的目标RCS起伏模型——Swerling模型研究目标散射系数的分布情况。

首先假设散射的相位变化 φm，n服从［0，2π］范围内的均匀分布，根据概率论知识可知Re(um，n)和Im(um，n)是独立同分布(用f(μ)表示概率密度函数)的随机变量，这样Re(xm，n)和Im(xm，n)也是独立同分布的(用f(x)表示分布概率密度函数)。按照Swerling起伏模型划分，目标RCS分别服从自由度为2和4的χ2分布，以下对两种目标起伏分布分别讨论:

a.SwerlingⅠ、Ⅱ型

b.SwerlingⅢ、Ⅳ型

3.2 MIMO雷达空间分集

通道数据之间的相关性是受空间分集的自由度影响的，因此下面对几种极端的空间分集情况进行讨论。

a.收发全不分集

当发射(接收)各单元之间间距很小(远小于到目标距离)时，所有通道传播路径一致，即各通道散射系数完全相关，空间自由度为1。

b.接收全分集

当发射各单元之间间距很小(远小于到目标距离)而接收各单元间距满足空间分集条件时，同一接收单元对应的通道传播路径一致，不同接收单元对应的通道传播路径完全独立，空间自由度为N。

c.发射全分集

当发射各单元间距满足空间分集条件而接收各单元之间间距很小(远小于到目标距离)时，同一发射单元对应的通道传播路径一致，不同发射单元对应的通道传播路径完全独立，空间自由度为M。

d.收发全分集

当发射(接收)各单元间距均满足空间分集条件时，所有通道传播路径完全独立，即各通道散射系数完全不相关，空间自由度为MN。

3.3 检测性能分析

根据不同的目标模型以及工作模式下的f(x⇀|H1)可以得到相应的统计检测量如表1所示。

表1 特殊情况下的统计检测量

其中g(x)=h(Re［x］)+h(Im［x］)。而h(x)表示检波函数，并与目标模型有关:对SwerlingⅠ、Ⅱ型有h1(x)=x2;对SwerlingⅢ、Ⅳ型有这里k=MN、M、N、1分别对应四种不同的工作模式的信噪比相干积累增益。以上是最大似然比检测下的统计量，可以看到SwerlingⅢ、Ⅳ型目标的检测量较复杂，而且对雷达来说一般采用一种检测方式，因此这里仅讨论平方律检波下两大目标类型检测概率:

对SwerlingⅠ、Ⅱ型目标:

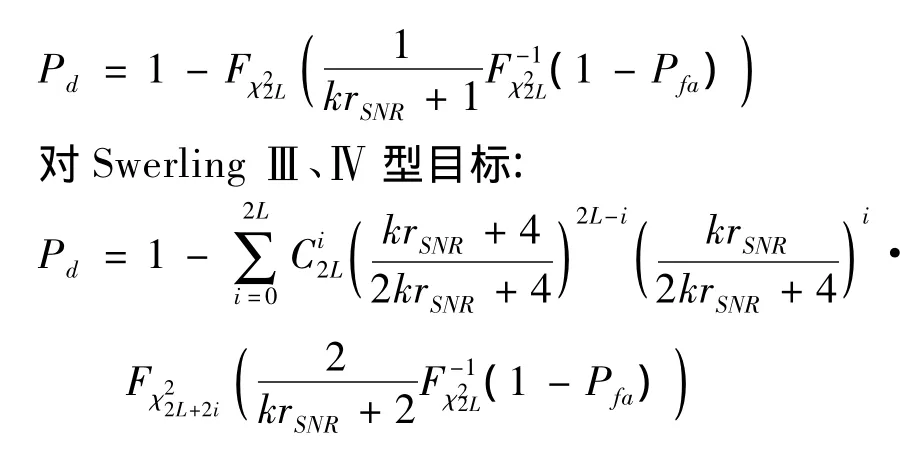
其中L=MN/k可以看成是MIMO雷达空间分集的自由度。一般来说，相干积累增益越大检测概率越高，也就是说SISO模式应该具有比MIMO模式更高的检测概率，但事实并不如此。图2是2发4收的MIMO雷达在虚警概率为10-5条件下四种模式分别对两大类型目标检测概率与信噪比的关系。可以看到在低信噪比的情况下SISO模式对SwerlingⅠ、Ⅱ型目标的检测概率确实较高，但随着信噪比的提高MIMO模式有更好的检测能力。如果将MIMO模式检测概率的提高归功于所谓的空间分集增益，而空间分集增益主要受空间自由度的控制，由于空间自由度和相干积累增益之间存在反比关系，因此空间分集增益与相干积累增益是无法兼得的。为了获得最佳的检测性能需要结合噪声环境选择合适的空间自由度。根据图2还可以知道在相同条件下MIMO雷达对SwerlingⅢ、Ⅳ型目标的检测性能和对SwerlingⅠ、Ⅱ型目标的检测性能基本一样甚至略优，而这里采用的还不是最优的检测方法。

图2 MIMO雷达检测概率与信噪比的关系

4 结论

MIMO雷达由于空间分集增益和相干积累增益的反比关系，对噪声环境作出估计以合理选择空间自由度才能获得最佳的检测性能。在N-P准则下，MIMO雷达对SwerlingⅢ、Ⅳ型目标的最优检测器较SwerlingⅠ、Ⅱ型目标的复杂得多，而在相同的检测条件下雷达对SwerlingⅢ、Ⅳ型目标比SwerlingⅠ、Ⅱ型目标具有更好的检测性能。

［1］E.Fishler，et al.MIMO radar:an idea whose time has come［C］.Proceedings of the IEEE Radar Conference，2004:71-78.

［2］E.Fishler，et al.Spatial Diversity in Radars-Models and Detection Performance［J］.IEEE Trans.on Signal Processing，2006:823-838.

［3］梁百川.对统计MIMO雷达的干扰［J］.舰船电子对抗，2009，32(1):5-8.

［4］戴喜增，彭应宁，汤俊.MIMO雷达检测性能［J］.清华大学学报，2007，47(1):88-91.

［5］丁鹭飞，耿富录，陈建春.雷达原理(第四版)［M］.北京:电子工业出版社，2009，3.

［6］张明友，吕明.信号检测与估计(第二版)［M］.北京:电子工业出版社，2005，2.