带冷罩的自旋弹头在液氮消耗时的姿态模型

余正宁 赵育善

（北京航空航天大学 宇航学院，北京 100191）

带冷罩的自旋弹头在液氮消耗时的姿态模型

余正宁 赵育善

（北京航空航天大学 宇航学院，北京 100191）

研究了带液氮冷屏蔽罩（冷罩）的自旋弹头在自由飞行段中，冷罩多孔介质层内液氮不断消耗时弹头姿态的变化规律.针对工程上无法利用数值计算直接研究多孔介质中液氮消耗对弹头姿态运动影响的问题，以均相模型分析多孔介质层内气液混合物的运动规律，建立了均相介质在离心力作用下的渗流运动方程.对此方程进行无量纲化，分析了均相介质的运动规律，得到了变质量弹头的姿态动力学模型.通过分析与仿真发现，自旋角速度随冷罩内液氮消耗而不断增大，非自旋方向角速度不为零时，其运动频率不断增大，且会产生运动阻尼，但频率变化很小，运动阻尼量级也极小，工程中可忽略冷罩中液氮消耗对非自旋方向的影响.

冷屏蔽罩;渗流;多孔介质;姿态动力学模型

为了达到弹头红外隐身的目的，美国物理学家协会提出了用液氮冷屏蔽罩（简称冷罩）冷却弹头的方案［1］.冷罩由双壁面锥体构成，内外壁之间形成空腔，通入液氮，液氮在双壁面形成的空隙间流动与蒸发，使冷罩维持在低温条件下，进而实现红外隐身的目标.为使液氮在空腔中分布均匀，在腔内填充多孔介质材料.

研究表明［2］:携带冷罩的弹头在5μm波段的红外辐射能量比没有携带冷罩的普通弹头低1012倍，对于导弹拦截器上5 μm波段红外探测器，这意味着原来可发现距离1 000 km处的普通弹头，却只能发现距离1 m处的携带冷罩的弹头.因此，冷罩在弹道导弹红外隐身方面非常有应用前景.

当前，国内外有关冷罩的研究资料很少，仅有的资料也只是针对冷罩的热交换机理［2］、结构设计与热应力［3－4］等进行分析.总体设计师们则更关心冷罩及其内部液体对弹头轨道、姿态的影响，而这方面的研究尚无公开报导.液氮在冷罩多孔介质内运动极其复杂，不仅需要考虑液氮挥发后的气液混合物的运动、还要分析混合物在多孔介质中的渗流运动，很难用数值仿真直接对其动力学特性进行研究，而工程应用中希望建立简单、有效的力学模型来描述液氮运动对弹头运动的影响，目前为止，并未发现相关的工程模型.

本文以两相均相模型分析多孔介质层内气液混合物的运动规律，建立了离心力作用下的均相介质渗流运动方程.经无量纲化分析，总结出多孔介质层中气液混合物的运动规律，得到均相介质在冷罩中的质量变化模型，进而建立了可用于工程实际的姿态动力学模型.

1 多孔介质中的液氮运动分析

1.1 两相均相模型

液氮在多孔介质层中蒸发、流动，表现为气液两相.处理两相流问题有两种模型:两相均相模型与两相分相模型，前者指的是把两相介质看成均匀介质，介质的参数取两相平均参数，然后再根据单相均匀介质建立两相流基本方程;后者把两相分成两种单相流动（气相和液相），介质参数分别取各自的介质参数.

两相均相模型认为相变过程没有严格的气液界面存在，气态和液态共同存在，该模型计算简单;两相分相模型能较精细地反映出相变的过程，但计算量和难度都较大，不便工程应用.本文采用两相均相模型.

1.2 多孔介质中渗流方程

工程上一般采用渗流力学来研究液体在多孔介质中的运动，其对大量流体质点利用统计平均方法来定义流体的速度、压力、密度等宏观物理量，并对这些物理量在空间的分布规律和随时间的变化规律进行理论研究和数值计算.

各向同性多孔介质中，液体渗流运动方程［5］为

式中，u为渗流速度;μ为流体的动力粘性系数;ρ为密度;p为流体压力;ε为多孔介质的孔隙率;fg为离心加速度;κ为渗透系数;CF为无量纲常数.

方程式（1）中等号右边依次为离心力项、压力降项、粘性力项、渗透阻力项.渗透阻力可由Darch定律或者加上非线性修正的Darch-Forchheimer定律［6－7］得到，其第 1 部分是与速度成正比的线性部分，第2部分是当速度较大时作修正而附加的非线性部分.

渗透阻力可以根据厄贡（Ergun）方程［8］进行描述，即

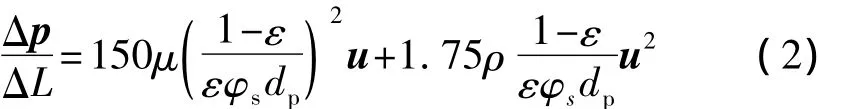
式中，Δp为流体通过厚度为ΔL的多孔介质层的压力降;φs为多孔介质中固体颗粒的形状系数;dp为多孔介质颗粒的当量直径.

1.3 渗流方程的无量纲化

液体渗流运动受液体各运动参数以及多孔介质性质影响，直接求解极其困难，本文对其进行定性分析.为使分析更具一般性，将渗流运动方程进行无量纲化.首先引进无量纲物理量（带*表示）:

式中，T为特征时间;L为特征长度;U为特征速度;P为特征压力.

引进无量纲参数:

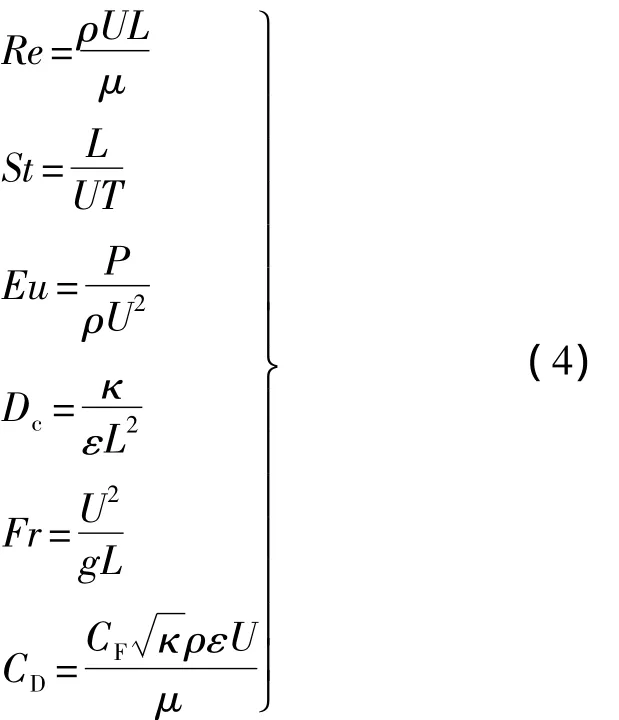
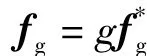
将式（4）代入渗流运动方程式（1）中，可得无量纲运动方程:

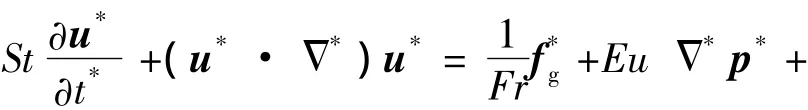
1.4 无量纲方程简化

式（5）中的渗透阻力项，其非线性项系数为

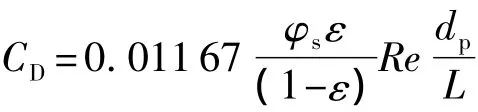
由于 dp/L很小，而 φsε/（1－ε）和 Re不是非常大，所以渗透阻力中非线性项远小于线性项，可将非线性项忽略.

式（5）中粘性力项与渗透阻力项的比可写为

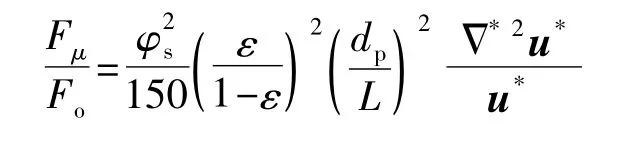
由于dp远远小于L，所以粘性力远小于渗透阻力，可以将其忽略.因此，可将式（5）写为

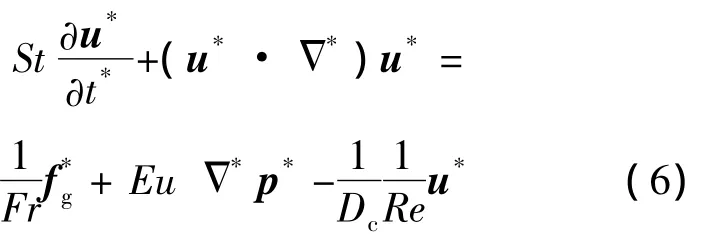
1.5 液氮运动分析

1）离心力分析.离心力只受弹头自旋角速度影响，与渗流性质无关，相对于液体运动来说，可以认为其为恒定值.将离心惯性力分解为沿腔方向的力F1与垂直于腔方向的力F2，如图1所示.

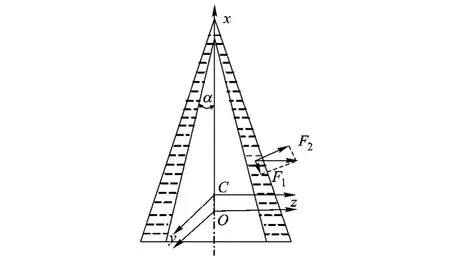
图1 离心力分解图

腔的厚度很小，所以在垂直于腔的方向，可以忽略液体运动.沿腔的方向，因为锥角很小，所以离心力分量F1也很小，离心力对该方向的液体运动的影响也可以忽略.

2）压力与渗透阻力分析.压力降变化值与欧拉数Eu有关，Eu数越大，其影响越大.由于沿速度方向压力变小，所以压力梯度为负值，即方程式（6）中压力降项为负.

由方程式（6）可得，渗透阻力不仅受多孔介质材料特性Dc影响，还与流体流动特性Re有关.一般情况下，Dc很小，而工程上常见的渗流Re也不是非常大，所以二者乘积仍然很小，故而导致渗透阻力很大，且其始终与速度方向相反.

由以上分析可知，压力降与渗透阻力导致的加速度均为负，即液体运动要克服较大的阻力，始终为减速运动.初始时液体运动速度不大，因此，在整个飞行过程中，液体均不会有太大的运动，即液氮分布变化不大.

3）液氮运动情况.综上所述，多孔介质层内液体分布在各项力的作用下不会发生太大变化，即均相介质的运动很小，可忽略其速度变化，但均相模型的参数，如密度，会随着液氮蒸发而改变.

由以上理论分析，可以合理假设冷罩多孔介质内一直充满均匀介质，该介质不发生对流等相对于弹头的运动，但密度会随液氮消耗而变化，导致弹头转动惯量变化，进而导致姿态改变.

2 弹头姿态动力学模型

2.1 坐标系定义

固连坐标系S1:原点O与不考虑液氮情况下弹头质心重合，x轴指向弹头前方，Oy垂直于弹头纵轴指向上，Oz与Ox，Oy成右手系.

本体坐标系S2:原点C位于弹头真实质心（考虑液氮），各轴与S1系各轴方向平行.

S1系与S2系如图1所示.

2.2 惯性矩阵计算

关于S2系3个坐标轴的转动惯量可写为

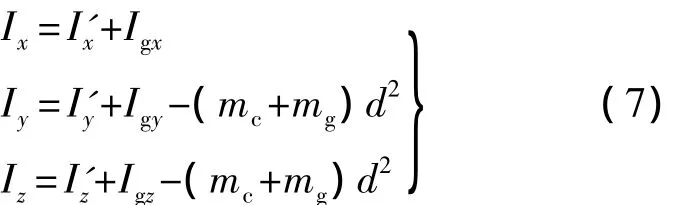
式中，mg为弹头刚性部分（包括多孔材料）的质量;mc为 t时刻均相介质质量;I'x，I'y，I'z以及 Igx，Igy，Igz分别为均相介质、弹头刚性部分（包括多孔材料）对S1系3个坐标轴的转动惯量;d为弹头质心C与S1系原点O点之间的距离.

2.3 均相介质密度变化

设液氮受热后均匀蒸发，消耗速率恒定，为Δm，g/s，初始时腔内充有质量为m1的液氮，则腔内液氮质量变化可写为

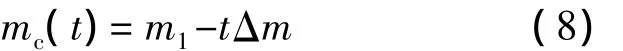
进而可得密度变化为

式中，ε为孔隙率;V为多孔介质层的体积.

由于多孔介质层体积、孔隙率均一定，液氮质量呈线性变化，所以均相介质密度也呈线性变化.

2.4 姿态方程

对冷罩质心应用动量矩定理，可得自旋弹头的姿态方程为

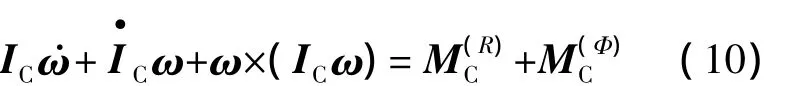
式中，IC为关于质心的惯性矩阵;为作用于刚体上的所有外力对质心的主矩;为所有反推力对质心的主矩.

3 姿态运动分析及仿真

3.1 理论分析

将其写为分量形式，有

由式（12a）可得

式中，Cx为常数，可通过初始转动惯量和角速度求得.将式（12b）变形为

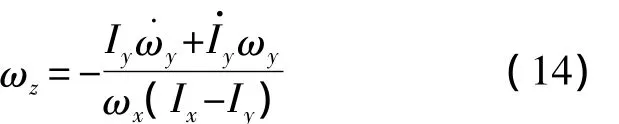
两边求导后，将求导结果与式（14）代入（12c）可得有关ωy的二阶微分方程，同样的方法可得到ωz的表达式.由于二者形式相同，可将其写为

其中

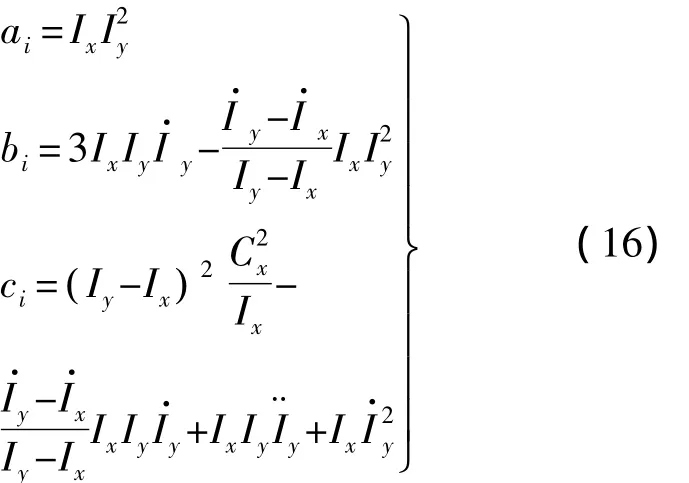
由式（13）、式（15）可知，非自旋方向姿态角速度变化为有阻尼振荡，频率与阻尼分别为

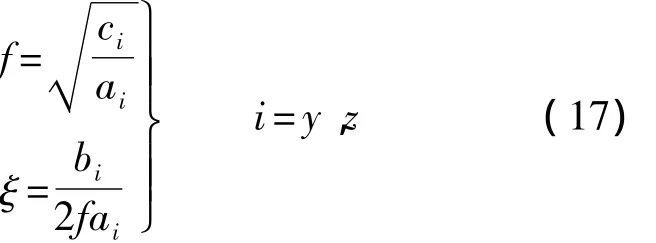
若无冷罩影响，则角速度为等幅无阻尼振荡，频率为

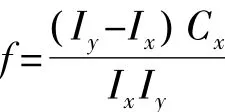
可见，冷罩的加入，不但使系统产生阻尼，而且也使频率随液氮消耗不断变化.

3.2 数值仿真

假设弹头质量为2000kg，高2.0m，弹头与冷罩的半锥角（图1中α）均为15°，多孔介质层厚度为1 cm.初始转动惯量为Ix=400，Iy=Iz=1000，初始姿态角速度为 ωx=2π rad/s，ωy=0.01 rad/s，ωz=0.02 rad/s.初始时刻多孔介质层内充满液氮，飞行过程中液氮以15 g/s的消耗量减少，则液氮、弹头的转动惯量变化如图2、图3所示.

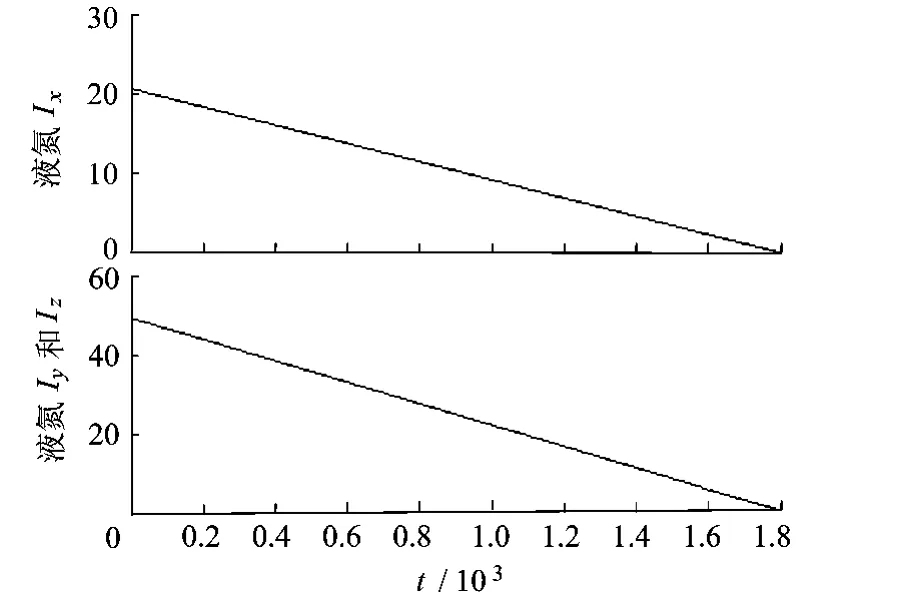
图2 液氮的转动惯量变化

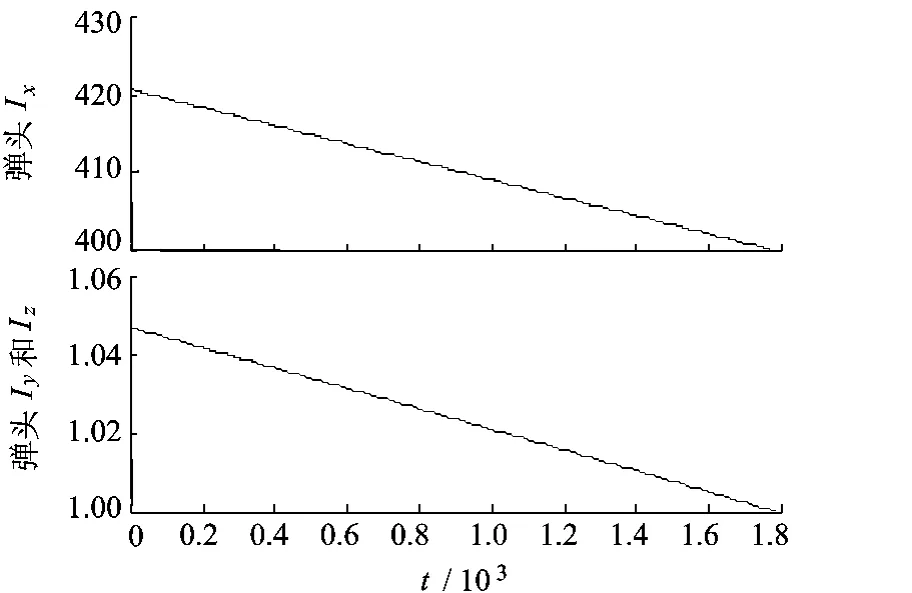
图3 弹头的转动惯量变化

由图2、图3可以看出，对3个坐标轴的转动惯量基本都是线性变化.其原因在于，多孔介质层内液氮消耗速度均匀，则腔内均相介质密度线性变化，导致其对各轴的转动惯量也线性变化.式（7）虽然不是线性表达式，但弹头质心距原点O的距离d太小，其影响可以忽略，则计算所得的转动惯量基本呈线性.

不考虑冷罩时，角速度变化频率为

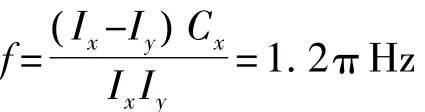
冷罩内液氮分布对弹头的姿态角速度变化频率、阻尼及角速度大小影响如图4所示.

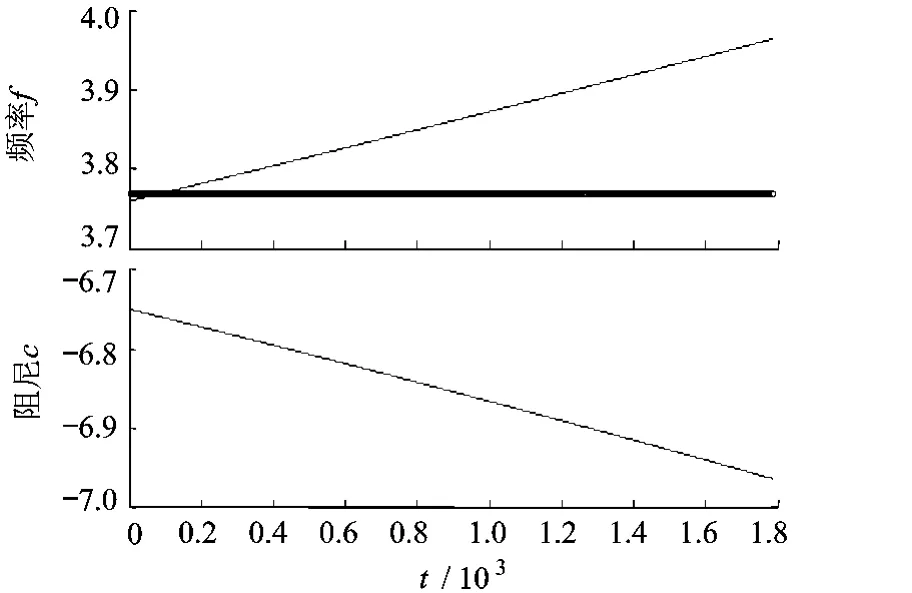
图4 频率、阻尼变化图

由图4可知，非自旋方向姿态角速度的运动频率随着液氮消耗不断增大，由约3.76 Hz增大到约3.96 Hz，接近线性增长，但影响作用不是很大，每百秒增大约0.1 Hz.角速度运动阻尼非常小（量级为10－6），对姿态角速度的影响可以忽略，角速度仍近似为等幅振荡，如图5所示.

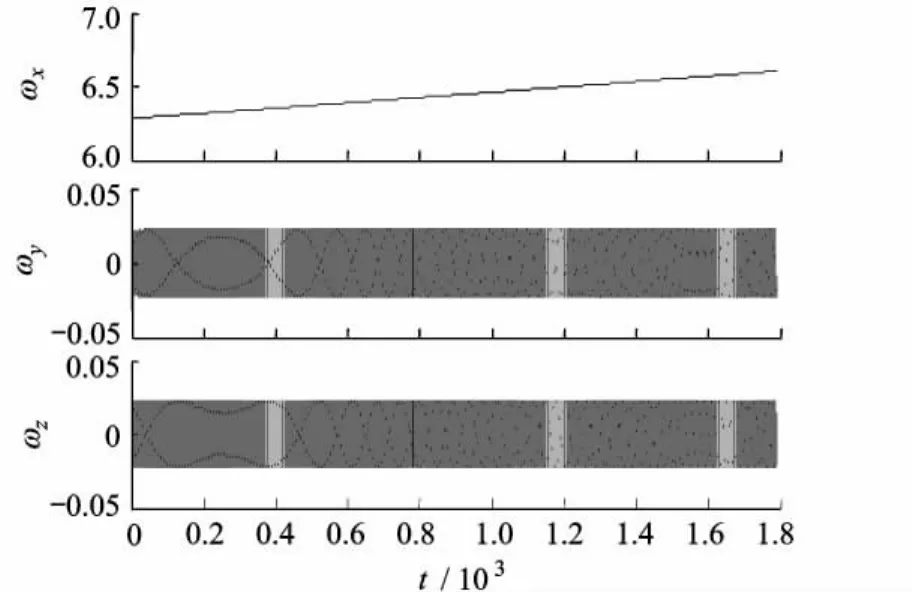
图5 姿态角速度

自旋方向的角速度随液氮消耗而不断增大，究其原因，是因为该方向转动惯量随液氮消耗而减小，根据式（13）可知，转动惯量减小时角速度增大.

4 结论

由本文中液氮均相模型以及弹头姿态动力学模型可得以下结论:

1）均相模型在多孔介质层内的速度变化不明显，故认为腔内介质不发生运动，充满整个多孔介质层，仅随着液氮消耗而发生密度改变，进而导致腔内质量分布变化，影响弹头姿态运动.

2）液氮的消耗使得自旋方向转动惯量不断减小，导致自旋角速度不断增大.

3）非自旋角速度不为零时，液氮消耗使得角速度运动频率有所改变，但改变缓慢且幅度不大，同时，会使角速度运动方程中出现阻尼项，但阻尼值很小，可以忽略其对非自旋方向角速度的影响，角速度仍近似做等幅振荡.

综上所述，带冷罩的自旋弹头在自由飞行过程中，液氮消耗仅会影响到自旋方向运动，对非自旋方向运动影响很小，工程应用中可以忽略.

致谢 感谢骆振华师弟在研究过程中所做的相关配合工作.

（References）

［1］Sessler A M，Cornwall J M，Dietz B，et al.A nuclear warhead with a cooled shroud［J］.Countermeasures，2004，4:105－113

［2］杨昌宝.液氮冷屏蔽罩换热机理研究［D］.南京:南京理工大学动力工程学院，2007

Yang Changbao.Mechanism investigation on heat transfer of Liquid-nitrogen cooled shroud［D］.Nanjing:School of Energy and Power Engineering，Nanjing University of Science ＆ Technology，2007（in Chinese）

［3］范燕萍.冷罩的结构设计与应力分析［D］.南京:南京理工大学机械工程学院，2007

Fan Yanping.Structure design and stress analysis of cooled shroud［D］.Nanjing:School of Mechanical Engineering，Nanjing University of Science ＆ Technology，2007（in Chinese）

［4］柴玉强.飞行器冷罩的结构设计与特性分析［D］.南京:南京理工大学机械工程学院，2008

Chai Yuqiang.Structure design and characteristic analysis of cooled shroud［D］.Nanjing:School of Mechanical Engineering，Nanjing University of Science＆ Technology，2008（in Chinese）

［5］陈金娥.关于渗流中流线不封闭的特性［J］.力学季刊，2003，24（3）:346－350

Chen Jine.Characteristics and conditions of unclosed flow streamline in porous media ［J］.Chinese Quarterly of Mechanics，2003，24（3）:346－350（in Chinese）

［6］Pascal J P，Pascal H.Pressure diffusion in unsteady non-Darcian flows through porous media［J］.Eur J Mech，B/Fluids，1995，14（1）:75－90

［7］Pascal J P，Pascal H.Non-linear effects on some unsteady non-Darcian flows through porous media［J］.Int J Non-Linear Mechanics，1997，32（2）:361－376

［8］霍华德F拉塞.化学反应器设计（I）:原理与方法［M］.北京:化学工业出版社，1982

Rase H F.Chemical reactor design for process plants:principles and techniques［M］.Beijing:Chemical Industry Press，1982（in Chinese）

Attitude model of spinning warhead with cooled shroud when liquid nitrogen is consuming

Yu Zhengning Zhao Yushan
（School of Astronautics，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

An attitude dynamics model of spinning warhead flying at free stage with a cooled shroud was established while liquid nitrogen filled in porous medium layer was consuming.The effect of liquid nitrogen movement to spinning warhead is difficult to calculate and simulate directly in engineering，according to this，an infiltration movement model of mixture in porous medium was gained by using homogeneous assumption，then was analyzed by applying dimensionless method，and an applied attitude model was obtained.Simulation shows that angular velocity is increasing in spinning direction，but in other directions，frequencies of angular velocities are increasing while these velocities are not zero，meanwhile，damp effects are appeared in the angular movement.Because of little impaction to attitude angular，both frequencies increase and damp effects could be ignored in practical project.

cooled shroud;infiltration;porous medium;attitude dynamics model

V 412.4

A

1001-5965（2012）02-0208-05

2010-11-03;< class="emphasis_bold">网络出版时间:

时间:2012-02-21 11:47;

CNKI:11-2625/V.20120221.1147.022

www.cnki.net/kcms/detail/11.2625.V.20120221.1147.022.html

余正宁（1984－），男（回族），宁夏海原人，博士生，null_yzn@139.com.

（编 辑:张 嵘）