MEMS 陀螺随机误差的建模与分析

王新龙 李 娜

（北京航空航天大学 宇航学院，北京 100191）

MEMS 陀螺随机误差的建模与分析

王新龙 李 娜

（北京航空航天大学 宇航学院，北京 100191）

为了更全面地了解微机电系统（MEMS，Micro-Electro-Mechanical Systems）陀螺仪的随机漂移误差随时间变化的特性，利用动态Allan方差分析法对MEMS陀螺仪输出信号特性进行了全面分析.首先介绍了Allan方差和动态Allan方差分析法原理，然后分别利用Allan方差分析法和动态Allan方差分析法对MEMS陀螺仪的实测数据进行了特性研究与性能分析.研究结果表明:速率斜坡、量化噪声和速率随机游走是MEMS陀螺的主要随机噪声，并且MEMS陀螺的随机漂移具有随时间变化的不稳定性.动态Allan方差不仅可以分离和辨识出MEMS陀螺的主要随机误差源，而且可以跟踪和描述信号随时间变化的稳定性，因此动态Allan方差较经典Allan方差分析法能够更全面地表征MEMS陀螺仪的性能.

MEMS陀螺;漂移误差;Allan方差;动态Allan方差

与传统陀螺仪相比，微机电系统（MEMS，Micro-Electro-Mechanical Systems）陀螺仪具有体积小、重量轻、成本低、抗冲击、可靠性高等优点，在低成本导航系统中获得了越来越广泛的应用.但MEMS陀螺仪的精度相对较低，这极大地限制了其应用范围.因此，如何补偿MEMS陀螺仪的漂移误差以提高陀螺仪的测量精度，已成为MEMS陀螺仪研究工作的重点之一.

陀螺仪漂移一般分为确定性漂移和随机漂移两部分，确定性漂移通过陀螺测试和标定试验加以补偿.随机漂移是无规律且随时间变化的，一般方法是通过建立陀螺的时间序列随机漂移模型，然后利用滤波器对建模后的残差进行滤波，以降低随机漂移误差对陀螺精度的影响.

目前绝大多数文献都是采用Allan方差法对MEMS陀螺仪随机噪声特性进行分析.Allan方差分析是在时域上对频率稳定性进行分析的一种通用方法［1］.然而 Allan方差也有不足之处，经典Allan方差一般用来分析信号的稳定性，它对理想的时变信号是有效的，而实际的误差信号，即使在极短的时间间隔内，信号也表现出不稳定性，况且在长时间内，被测信号受到温度、湿度和其他器件物理性能的改变而变化.动态Allan方差是用来测量原子钟时变稳定性的工具，它可以揭示受湿度变化、温度变化、辐射干扰、突然故障、老化等各种因素影响的原子钟平稳性的变化［2］.目前，动态Allan方差已被成功应用于伽利略实验卫星GIOVE的时钟监控［3］，同时也被用来监测 GPS（Global Positioning System）时钟的稳定性［4］.

本文应用动态Allan方差分析法对MEMS陀螺仪输出随机误差信号特性进行了建模与分析，结果表明动态Allan方差分析法不仅能确定MEMS陀螺仪各种随机漂移的系数，而且还可以跟踪和描述信号随时间变化的稳定性.

1 时间序列分析建模方法

采集到陀螺仪实测信号后，首先通过速率试验法对陀螺仪确定性误差分量进行标定.确定性漂移误差标定后，通常再利用时间序列分析法确定随机漂移误差的特性.MEMS陀螺仪随机误差时间序列分析法建模与补偿流程见图1，其建模步骤［5］可归纳为:首先对测得的数据样本进行预处理，包括奇点的剔除、趋势项的去除和周期项的去除;其次对预处理后的数据序列进行统计检验，包括平稳性检验、周期性检验和正态性检验.

图1 利用时间序列分析法的陀螺仪误差建模流程图

若经过上述预处理后的残差序列是平稳时间序列，则可利用平稳时间法建立其误差模型，首先确定所要拟合模型的类别和阶次;其次估计模型参数并进行适用性检验;最后对所建立的模型进行变换，使之成为连续微分方程，便得到可利用Kalman滤波器处理的系统状态模型和量测模型.

2 Allan方差和动态Allan方差原理

2.1 Allan 方差原理

Allan方差是一种在时域上对频域稳定性进行分析的方法.Allan方差的特点是它不仅能够确定产生数据噪声的基本随机过程的特性，而且能够识别给定噪声项的来源［6］.

在进行Allan方差的分析时，由于陀螺仪类型和数据测试环境等的不同，陀螺仪输出数据中可能存在各种成分的随机噪声.如果各噪声源统计独立，则计算的Allan方差是各类型误差的平方和［7］，即

式中，τ为相关时间，s.

式（1）中包含角随机游走（ARW，Angle Random Walk）（系数用N表示）、偏差不稳定性（BI，Bias Instability）（系数用 B表示）、速率随机游走（RRW，Rate Random Walk）（系数用 Kr表示）、速率斜坡（RR，Rate Ramp）（系数用 R表示）、量化噪声（QN，Quantization Noise）（系数用Q表示）、指数相关噪声（MN，Markov Noise）、正弦噪声（SN，Sinusoidal Noise）.

式（1）中各主要误差项都可表示成正比于τ的－2～+2次幂的系数表达式，因此式（1）可简化为

其中，An分别对应与 QN，ARW，BI，RRW，RR 各噪声相关的拟合多项式系数，n=－2，－1，0，+1，+2.

根据不同的τ对应的Allan方差，对式（2）进行最小二乘拟合，可以求得拟合多项式系数，进而求得各噪声源系数.

2.2 动态Allan方差原理

动态Allan方差是经典Allan方差的扩展，它是以一种非常直观的方式定义的:如果认为一个代表相位或频率误差（或任何其他物理量）的随机信号 （x t）具有时变特性，那么可以在不同的时间段内重复估计信号的Allan方差，例如在时间点t，以长度为N的矩形窗截断随机信号 （x t），估计此截断信号的Allan方差.在每个时间点t做同样的分析，然后综合每个时间间隔内获得的方差值，即可得到随机信号的动态 Allan方差［8－9］.

评估信号稳定性的标准是Allan方差［10］:

这里〈〉表示求时间段内的总体平均.

如果

则式（3）可以写成如下形式:

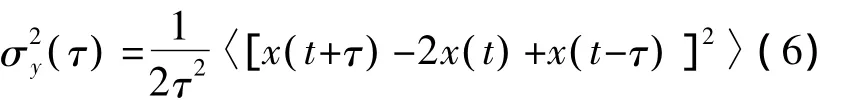
对于离散信号

Allan方差是在给定观测间隔τ的情况下，以二维图的形式描述信号的误差特性，而动态Allan方差是在给定时间t和观测间隔τ的情况下，以三维图的形式来描述随机信号的稳定性信息.

当存在外界干扰时，信号稳定性会随着时间而变化，可以用动态Allan方差描述这种变化:

由于动态Allan方差描述的是信号随着时间变化的平稳性信息，因此，利用动态Allan方差分析非平稳随机过程，既可以得到陀螺仪随机漂移的各噪声项系数，又可以分析随机误差随时间变化的稳定性.

3 MEMS陀螺实测数据分析

本文在实验室标准三轴转台上对MEMS陀螺仪进行速率实验，分别记录输入不同角速率时陀螺仪的输出数据.陀螺1随机误差输出如图2所示，其Allan方差分析和动态Allan方差（选取N=100）分析曲线如图3和图4所示.

图2 陀螺1随机误差输出曲线

图3 陀螺1随机误差Allan标准差相关时间曲线

图4 陀螺1随机误差的动态Allan方差曲线图

由图3可以看出:在τ=1～7 s内，曲线斜率近似为－1/2，主要表现为角随机游走噪声，说明陀螺受外界干扰影响较大，在τ=7～8 s内，曲线斜率趋近－1，主要表现为量化噪声，在τ=8～10 s内，曲线斜率近似为0，主要表现为零偏不稳定性噪声.在τ=10～30 s内，曲线斜率近似为－1/2，角随机游走在发挥作用，随后Allan标准差表现为速率随机游走、角度随机游走和速率斜坡交替出现，并与各种噪声叠加，而在曲线后段出现正弦状震荡，可以理解为信号中含有低频的正弦噪声并伴有一定的速率随机游走噪声.同时，也可看出MEMS陀螺随机误差的多样性.

通过以上分析可以得到:MEMS陀螺仪的角随机游走噪声分布在高频部分，量化噪声分布在略低频段，零偏不稳定性频率更低，而速率随机游走和速率斜坡频率最低.另外，由图4可以进一步看出:随着时间的变化，MEMS陀螺仪输出数据的动态Allan方差起伏较大，说明陀螺具有随时间变化的不稳定性.

为了进一步验证动态Allan方差在分析陀螺仪输出随机噪声信号特性方面的有效性，选取陀螺2的实测数据进行Allan方差和动态Allan方差分析，其结果如图5～图7所示.从图中可以看出:动态 Allan方差示意图 τ-σ（t，τ）坐标轴的投影即为经典Allan方差，动态Allan方差在时间轴上反映了噪声的突变，而经典Allan方差不包含此信息.

图5 陀螺2随机误差输出曲线

图6 陀螺2随机误差Allan标准差-相关时间曲线

图7 陀螺2随机误差的动态Allan方差曲线图

2组陀螺仪输出数据的Allan方差法拟合噪声项系数如表1所示.

表1 Allan方差拟合的陀螺噪声项系数

由表1可以看出，对于陀螺1而言，速率斜坡、速率随机游走和量化噪声的系数较大，因此它们是主要误差源.而陀螺2的主要噪声为速率斜坡、速率随机游走和偏差不稳定性.

比较2组MEMS陀螺仪输出噪声项系数可以得出:

1）陀螺2的量化噪声系数较小，说明其数据采集系统是比较理想的，而陀螺1量化噪声较大，可以通过提高采样系统的精度和缩短初始采样时间来减小此误差;

2）陀螺1的偏差不稳定性较陀螺2大很多，说明陀螺2电路部分存在较大误差，需要采取相应的滤波方法抑制此噪声;

3）陀螺2的速率随机游走较小，说明其漂移相对较小.随机游走噪声反映了MEMS陀螺仪的制造水平，因此，陀螺2的制造水平要高一些;速率随机游走占了误差较大部分，说明系统的马尔科夫过程是比较明显的，可用软件补偿的方法提高其精度;

4）可能由于外界环境影响陀螺温度的变化导致陀螺1的速率斜坡噪声较大.

利用动态Allan方差方法计算陀螺1的随机误差在不同时刻的噪声项系数如表2所示.

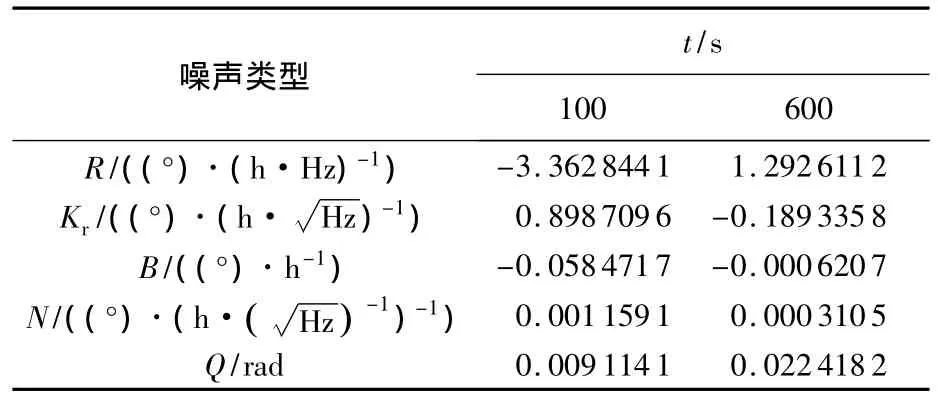
表2 动态Allan方差计算陀螺1噪声项系数

由表2可以得到，当t=100 s时，速率斜坡、速率随机游走和偏差不稳定性的噪声项系数较大，因此，它们是主要误差源.当t=600 s时，速率斜坡、速率随机游走和量化噪声是主要误差项.这说明了在不同的时刻，由于温度、湿度、干扰或器件物理性能等条件的变化，起主要作用的噪声项也在不断变化.

利用Allan方差以及动态Allan方差2种分析方法对MEMS陀螺仪输出的随机误差进行对比分析，可以看出:动态Allan方差在时间轴上反映了信号的瞬时稳定性，信号有突然变化时可以显示出来，而经典Allan方差却隐藏了这种变化.

4 结论

本文利用动态Allan方差法对MEMS陀螺仪实测数据进行了分析，结果表明:动态Allan方差法不仅可以分析陀螺仪的主要随机误差源，而且能够分析陀螺仪信号噪声的统计特性随时间的变化趋势.与传统的Allan方差分析法相比，它是一种更为有效的分析陀螺仪随机误差特性的方法.

将动态Allan方差应用于陀螺漂移误差信号的分析上，不仅可以分析信号频率的稳定性，还可以跟踪和描述信号随时间变化的稳定性.可见，动态Allan方差分析方法，不仅可用于MEMS惯性器件误差的建模与补偿，而且可用于对器件内部结构的改进和完善，另外在惯导独立导航以及与其他导航设备组合导航等应用方面都具有重要的推广应用价值.

（References）

［1］闾晓琴，张桂才.采用分段法估算Allan方差中的各噪声系数［J］.压电与声光，2009，31（2）:166－168 Lü Xiaoqin，Zhang Guicai.Estimation of various noise factors from Allan variance by subsection method［J］.Piezoelectrics ＆Acoustooptics，2009，31（2）:166－168（in Chinese）

［2］Galleani L，Tavella P.Tracking nonstationarities in clock noises using the dynamic Allan variance［C］//Frequency Control Symposium and Exposium，Proceeding of the 2005 IEEE International.Vancouver，BC:IEEE，2005:392－396

［3］Sesia I，Galleani L，Tavella P.Implementation of the dynamic Allan variance for the Galileo system test bed V2［C］//Frequency Control Symposium，2007 Joint with the 21stEuropean Frequency and Time Forum IEEE International.Geneva:IEEE，2007:946－949

［4］Galleani L.The dynamic Allan variance II:a fast computational algorithm［J］.IEEE Transaction on Ultrasonics，Ferroelectrics，and Frequency Control，2010，57（1）:182－188

［5］王新龙，杜宇，丁杨斌.光纤陀螺随机误差模型分析［J］.北京航空航天大学学报，2006，32（7）:769－772 Wang Xinlong，Du Yu，Ding Yangbin.Investigation of random error model for fiber optic gyroscope［J］.Journal of Beijing University of Aeronautics and Astronautics，2006，32（7）:769－772（in Chinese）

［6］Allan D W.Time and frequency（time-domain）characterization，estimation，and prediction of precision clocks and oscillators［J］.IEEE Transaction on Ultrasonics，Ferroelectrics，and Frequency Control，1987，34（11）:647－654

［7］IEEE Std 952-1997 IEEE standard specification format guide and test procedure for single-axis interferometric fiber gyros［S］

［8］Galleani L，Tavella P.The dynamic Allan variance［J］.IEEE Transaction on Ultrasonics，Ferroelectrics，and Frequency Control，2009，56（3）:450－460

［9］Nunzi E，Galleani L，Tavella P，et al.Detection of anamalies in the behavior of atomic clocks［J］.IEEE Transactions on Instrumention and Measurement，2007，56（2）:526－527

［10］Galleani L，Tavella P.Detection and identification of atomic clock anomalies［J］.Metrologia，2008，12（6）:127－133

Error modeling and analysis for random drift of MEMS gyroscopes

Wang Xinlong Li Na
（School of Astronautics，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

In order to comprehensively understand the characteristics of random drift error of micro-electro-mechanical systems（MEMS）gyroscope varying with time，the dynamic Allan variance was utilized to analyze the property of output signal of MEMS gyroscopes.Firstly，the theory of Allan variance and dynamic Allan variance were introduced.Then，the Allan variance and the dynamic Allan variance were utilized to analyze the characteristic and performance of the practical testing date of MEMS gyroscopes respectively.The study results show that the main random noise of MEMS gyroscope are the rate ramp，quantization noise and the rate random walk，and they are unstability varying with time.The dynamic Allan variance was utilized to not only extract and confirm some main noises of MEMS gyroscope，but also track and describe the stability of MEME gyroscope's signal varying with time.Consequently，compared with Allan variance，the dynamic Allan variance can represent the characterization of stochastic errors in MEMS gyroscope more comprehensively.

micro-electro-mechanical systems（MEMS）gyroscopes;drift error;Allan variance;dynamic Allan variance

V 241.5

A

1001-5965（2012）02-0170-05

2010-10-25;< class="emphasis_bold">网络出版时间:

时间:2012-02-21 11:46;

CNKI:11-2625/V.20120221.1146.018

www.cnki.net/kcms/detail/11.2625.V.20120221.1146.018.html

国家自然科学基金资助项目（61074157）

王新龙（1969－），男，陕西渭南人，教授，xlwon@163.com.

（编 辑:赵海容）