航天器扫描镜成像位置误差补偿技术
2012-06-22贾英宏徐世杰
贾英宏 徐世杰 陈 统
(北京航空航天大学 宇航学院,北京 100191)
航天器扫描镜成像位置误差补偿技术
贾英宏 徐世杰 陈 统
(北京航空航天大学 宇航学院,北京 100191)
研究地球静止轨道航天器两自由度扫描镜成像位置误差补偿问题,即通过对扫描角的补偿,使光轴在地球表面的成像点位置与标称位置相同,消除探测区域的位置偏差.在考虑扫描镜法线偏移、姿态偏差以及轨道误差条件下,推导了光轴成像点的地心经纬度计算公式.给出了上述3类误差的具体描述方式,并分析了各种误差对光轴成像点位置的影响关系.基于角度误差的小量假设条件,给出了扫描镜的步进角/扫描角补偿量的显式算法.针对法线偏移信息一般难以准确测量的问题,提出了一种利用扫描镜在特定工作模式下的光轴惯性空间定向能力和法线偏移的长周期特性对其进行估计的方法.仿真结果表明,所提出的补偿方案和算法能够显著提高成像点位置精度.
扫描;成像;地球静止轨道卫星;误差补偿;误差估计
传统的气象卫星多采用自旋姿态稳定控制方式,星上的扫描仪仅在步进方向具有一个自由度,配合卫星的自旋实现对地球的两维扫描[1].此类配置技术上较易实现,但在扫描效率、信号信噪声比等方面则存在固有缺陷.三轴稳定气象卫星由于在观测能力、观测方式以及观测灵活性等方面相比自旋卫星具有显著优势,目前已获得越来越广泛的应用,成为各国气象卫星的发展趋势.由于三轴稳定的姿态控制方式,此类气象卫星的扫描镜均采用两自由度扫描镜.在扫描过程中由于卫星轨道误差、姿态误差、扫描镜热变形等因素的影响,需要对扫描镜进行运动补偿,以提高扫描精度.
文献[2-3]研究了两自由度扫描镜运动对卫星平台姿态运动的影响,为扫描镜运动补偿提供了一定的理论基础.文献[4]利用开环姿态预估模型对卫星姿态进行预估,并基于预估姿态信息研究了扫描镜运动的补偿算法,以消除卫星姿态运动引起的扫描镜光轴指向偏差;文献[5-6]则利用闭环姿态预估方法达到上述目的.文献[7]则在卫星姿态信息已知的情况下研究了两自由度扫描镜的扫描角和步进角补偿问题,且没有做姿态偏差和补偿量的小量假设.文献[8-9]考虑了卫星姿态运动以及法线偏移等长周期系统误差的影响,给出了补偿算法,并讨论了利用光轴相对惯性空间的准确定向能力进行长周期系统误差估计的可能性.然而,文献[4-9]均未考虑航天器轨道误差的影响.然而,在航天器存在轨道误差的情况下,即使光轴相对瞬时轨道坐标系指向准确,光轴在地球表面的成像点位置仍然会与标称位置之间存在偏差,这会给图像导航带来困难;并且仅对于地球表面某些区域进行的区域扫描模式,这种位置偏差会造成预定扫描区域信息的丢失.因此,在扫描镜的补偿算法中,需要综合考虑轨道、姿态以及镜面法线偏移等因素,以消除成像点位置误差(像素偏移).
目前,有关的公开相关研究很少.文献[10]综合考虑了卫星轨道、姿态等误差的影响,给出了美国GOES I-M气象卫星的扫描镜补偿简化公式,但没有给出具体的推导过程和技术细节;文献[11]针对地球静止轨道卫星,综合考虑了姿态、轨道误差,给出了一种较文献[10]补偿精度更高的算法,但未考虑扫描镜法线偏移问题.
为此,本文以光轴在地球表面的成像点位置为指标,综合考虑卫星轨道误差、姿态误差和法线偏移的影响,给出成像位置偏差的补偿算法.由于扫描镜法线偏移信息一般不易测量,文中还提出了一种扫描镜法线偏移信息的估计方法,每隔一定的时间段利用光轴相对惯性空间的准确定向能力对法线偏移信息进行一次估计,并在补偿算法中进行更新.数值仿真结果表明,本文提出的补偿算法可有效提高光轴成像点的位置精度.
1 光轴成像点位置计算
考虑一个内部装有两自由度扫描镜的刚体航天器,如图1所示.Obxbybzb为航天器本体固连坐标系;Ogxgygzg为扫描镜支架坐标系,原点Og位于支架质心,xg指向南北驱动轴,与星体坐标系的xb指向一致,yg指向扫描镜的东西驱动轴,zg与xg和yg构成右手坐标系;Omxmymzm为扫描镜体坐标系,zm指向镜面标称法线方向,ym指向东西驱动轴方向,xm与ym和zm构成右手坐标系.定义zg轴与zb轴之间的夹角为(南北)步进角,由南向北为正,记为α;定义zm轴与zg轴之间的夹角为(东西)扫描角,自西向东为正,记为β.系统动力学模型参见文献[9].

图1 扫描镜结构及相关坐标系
记扫描镜法线方向矢量w在扫描镜体坐标系中的矢量列阵为wm,将其转换到卫星体坐标系中则有

式中,Abm为扫描镜体坐标系到卫星体坐标系的坐标转换矩阵,为扫描角β和步进角α的函数[8-9].对45°扫描镜,光轴在瞬时轨道坐标系中的方向余弦列阵为


如图2所示,E为光轴成像点,rs为瞬时轨道坐标系原点到成像点E的矢量,其模为Rs;r为卫星的地心矢量,模为卫星的地心距R;re为成像点E的地心矢量,模为地球半径Re.由余弦定理有
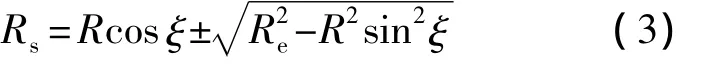
式中ξ为光轴矢量与瞬时轨道坐标系zr轴夹角,可由式(4)求得
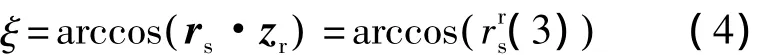
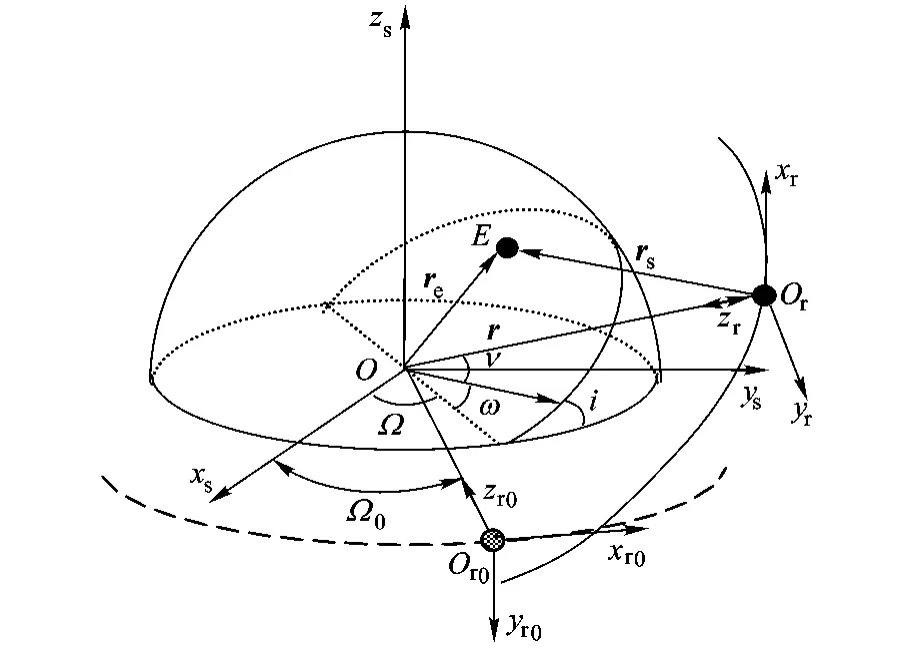
图2 各矢量之间的关系
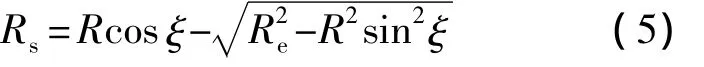
由各矢量的定义,显然有下述关系:

引入地心赤道旋转坐标系Oxsyszs,将式(6)在地心赤道旋转坐标系下描述,有

式中,右上标“s”和“r”分别表示该矢量在地心赤道旋转坐标系和瞬时轨道坐标系中的列阵表达式;Asr为瞬时轨道坐标系到地心赤道旋转坐标系的坐标转换矩阵,可写为

式中,Asr0为标称轨道坐标系到地心赤道旋转坐标系的坐标转换矩阵,对地球静止轨道卫星为常值矩阵,即

式中,Ω0为标称轨道的星下点经度;对非地球静止轨道卫星,Asr0可由轨道要素和格林威治恒星时角计算得到;Ar0r为瞬时轨道坐标系到标称轨道坐标系的坐标转换矩阵,下一节中将给出其具体表达式.由式(7)有

于是成像点的地心纬度为

成像点的地心经度为
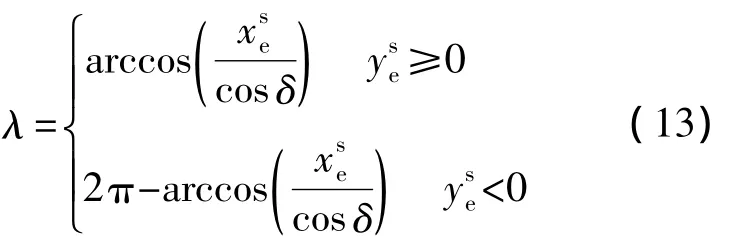
式中,地心纬度δ的定义区间为-π/2≤δ≤π/2,地心经度的定义区间为0≤λ<2π.
2 误差源描述及成像点位置偏差
成像点标称位置的定义条件为:
1)扫描镜法线无偏移;
2)卫星为理想的对地稳定状态;
3)卫星轨道为标称的地球静止轨道;
4)扫描角和步进角分别为标称值α0和β0.
在如上条件下,成像点在地球表面的位置为标称位置.
然而,在实际工作过程中,由于各种误差因素的影响,成像点可能偏离标称位置.本文中考虑的误差源有:
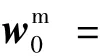

在小角度条件下坐标转换阵Aτ可写为

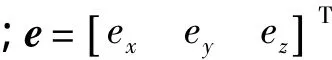

式中,Δτx=exΔτ;Δτy=eyΔτ.这一误差直接体现在式(1)法线指向的列阵表达式wm中.
2)姿态偏差.理想对地状态下,卫星三轴姿态为0,此时Arb为单位阵;姿态有小偏差时,采用3-1-2旋转顺序的欧拉角描述卫星姿态,则Arb可近似写为
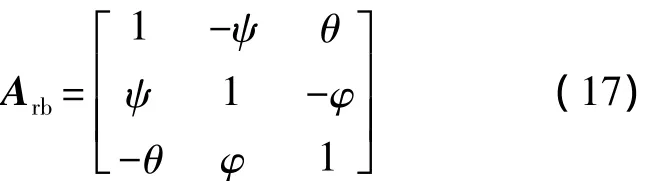
式中,φ,θ和ψ分别为卫星的滚动角、俯仰角和偏航角.
3)轨道误差.卫星标称轨道为地球静止轨道,而卫星的瞬时轨道与标称轨道之间存在一定误差,记卫星瞬时轨道升交点经度为Ω,可由升交点赤经和格林威治恒星时角计算得到;定义ΔΩ=Ω-Ω0,则瞬时轨道坐标系到标称轨道坐标系的坐标转换矩阵Ar0r可写为
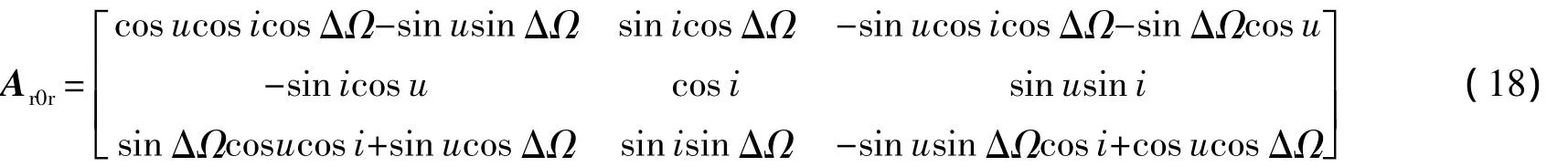
式中,i为轨道倾角;u=ω+ν为纬度幅角,其中ω为近地点幅角,ν为真近点角.轨道倾角i一般为小量,而u和ΔΩ均不是小量.但在轨道保持的控制作用下,u+ΔΩ则可视为小量.于是Ar0r可近似写为
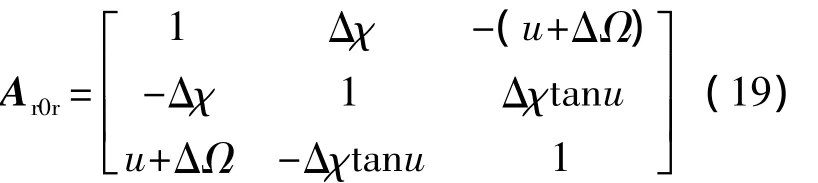
式中,Δχ=icosu.
上述轨道误差影响到式(8)中的坐标转换矩阵Asr,从而对光轴成像点位置产生影响.除上述轨道误差外,影响光轴成像点位置的还有卫星的地心距R,由式(5)和式(11)可见,R的大小与成像点位置直接相关.
若记成像点标称地心经度和纬度分别为λ0和δ0,成像点实际地心经度和纬度分别为λ和δ,则位置偏差定义为相应的经度和纬度误差如下:

3 补偿算法
记步进角补偿量为Δα,扫描角补偿量为Δβ,由于误差源中的角误差均可视为小量,因此补偿量也可视为小量,于是有

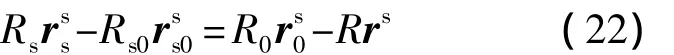
式中右下标“0”均表示相应矢量的标称值.将式(22)转换到标称轨道坐标系中描述有
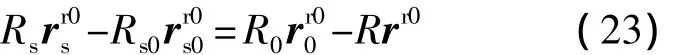
式中右上标“r0”表示在标称轨道系中描述该量.
在姿态角偏差、扫描镜法线偏移以及步进/扫描角补偿量均为小量的条件下,可由式(2)得到在z轴上的分量为r
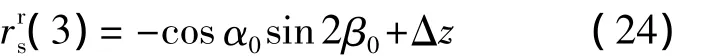
其中

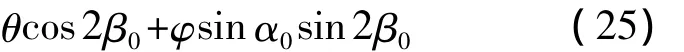
由式(4)显然有
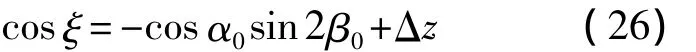
由式(26)忽略高阶小量可得:

将式(26)和式(27)代入式(5),并在Δz=0附近利用一阶泰勒展开可得

其中

获得以上基本量后,由式(23)可得3组方程,但只有两组独立,取其中前两组方程有
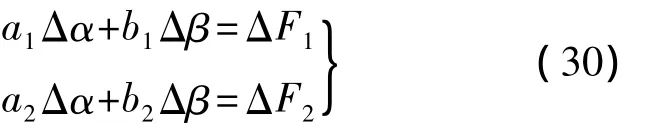
其中
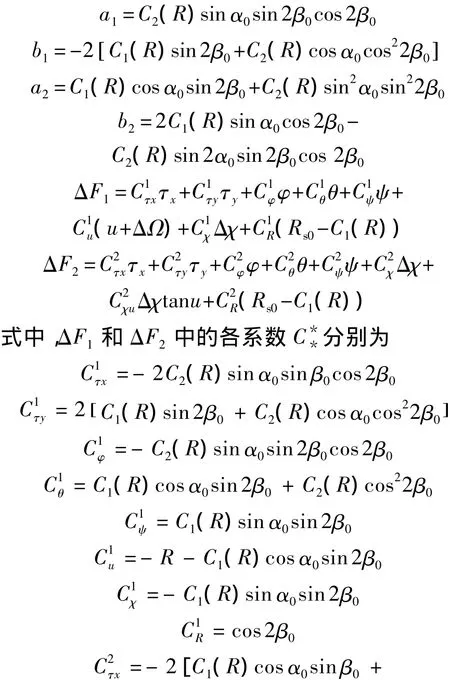

由式(30)可解得相应的扫描角和步进角补偿量计算公式分别为
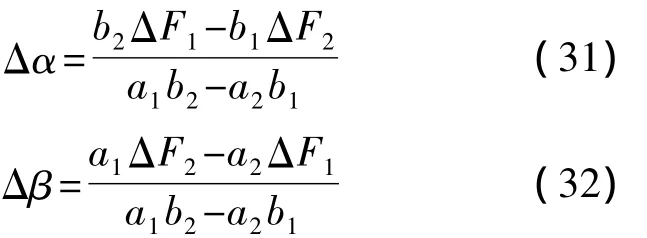
由于轨道误差基于经典轨道要素变换得到,因此上述补偿算法不仅适用于地球静止轨道卫星,也同样适用于其他类型轨道的卫星.
4 法线偏移信息的估计
相关研究表明,由热变形等因素引起的扫描镜法线偏移通常是引起扫描误差的主要原因[12],但扫描镜法线偏移不易测量和建模,而扫描镜的恒星敏感模式为偏移信息的估计提供了可能性.
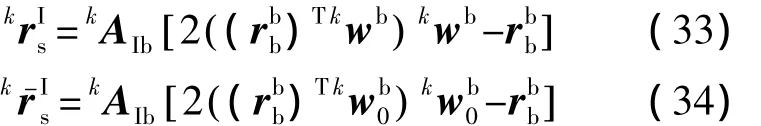
式中各变量的左上标“k”表示该变量在第k次恒星敏感时刻的值,以下均同.AIb为星体坐标系到惯性坐标系的坐标转换矩阵.
以上两式相减可得
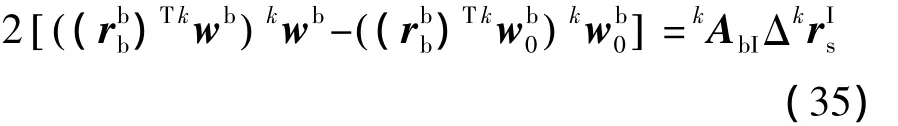
其中
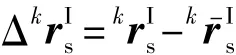
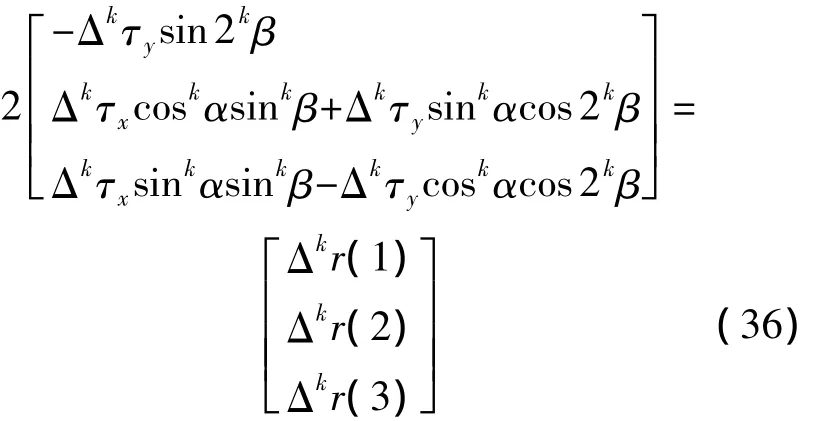
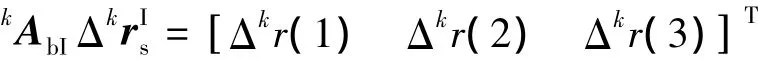

在第k次恒星敏感后即可利用式(37)和(38)得到法线偏移参数的估计值 Δkτy和 Δkτx,将其代入补偿算法(31)和(32)中即可在第k次与第k+1次恒星敏感时间段内对法线偏差进行补偿.此后每进行一次恒星敏感,可重新对法线偏移参数进行一次估计并对补偿算法中的相应参数进行更新.
需要指出,本部分给出的估计算法有两个应用条件:①法线偏移为慢变量,即两次恒星敏感时间段内法线偏移变化不大.由于法线偏移通常由加工误差(常量)和热变形(一般随轨道周期变化)引起,而恒星敏感通常几十分钟即可进行一次,远小于地球静止轨道卫星的轨道周期,因此这一条件可以满足;②卫星相对惯性空间的姿态信息足够精确.这是由于在光轴相对惯性空间的指向估计式(34)中并没有考虑坐标转换阵AIb的误差,若AIb误差较大,则指向估计式(34)具有较大误差.目前星敏感器已成为高精度三轴稳定卫星的首选姿态敏感器,其姿态测量精度可达角秒级,且在估计算法中仅需要卫星的惯性姿态,因此可认为卫星的惯性姿态信息是准确的.
5 数值仿真
仿真中卫星标称轨道为星下点经度为东经105°的地球静止轨道.卫星的实际初始轨道参数取为:升交点赤经为 105.5°;轨道倾角为 0.5°;轨道半长轴 4.2164×107m;偏心率0.001;近地点幅角0°;初始真近点角0.1°.初始时刻格林威治恒星时角G0=0°.轨道动力学中考虑地球扁率J2~J4项摄动.
卫星本体的惯量矩阵为

扫描镜惯量矩阵为
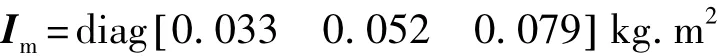
扫描镜支架的惯量矩阵为
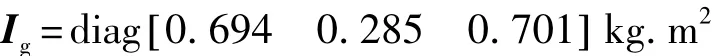
卫星姿态控制律为

其中ω0为轨道角速率,而
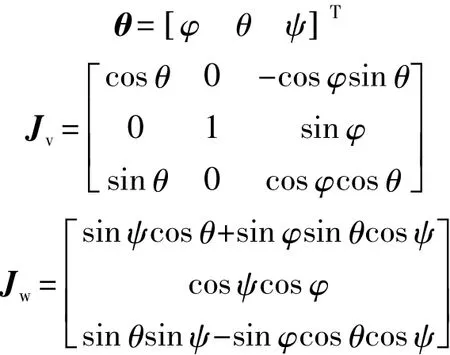
Kp和Kd为姿态控制参数,取为

卫星的初始姿态角为
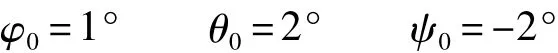
初始三轴惯性角速度均为0.
扫描镜的法线偏移欧拉转轴方向为

法线偏移角度为
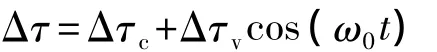
式中,Δτc=0.0115°;Δτv=0.0057°.
扫描镜的初始步进角为1°,初始扫描角为-46.5°.扫描规律包括3种模式:区域扫描模式,回扫模式和恒星敏感模式.具体过程为
1)t=50 s时扫描镜由初始位置开始第1次区域扫描,一次区域扫描东西扫描120行,每行扫描角共变化3°,用时2 s;南北步进角在东西加、减速过程中完成,每行步进角0.016 8°,120行扫描步进角共步进119次,步进角共变化2°.一次区域扫描共用时240 s;
2)第1次区域扫描后扫描镜驻留5s,之后开始回扫.回扫过程中扫描角不变,步进角以匀加速-匀速-匀减速规律回到初始位置,整个回扫过程用时5 s;
3)回扫后扫描镜在初始位置驻留5 s,开始进行恒星敏感.首先步进角和扫描角线性加速2 s,之后匀速转动6s,再线性减速2s,运动到步进角为13°,扫描角为-55.5°的位置,在此位置驻留20 s用以敏感恒星,之后按照相反的运动规律返回初始位置.整个恒星敏感过程共用时40 s;
4)恒星敏感后在初始位置驻留5 s,开始第2次区域扫描,扫描规律与第1次完全相同.第2次区域扫描完成后扫描镜保持静止不动.
图3和图4分别给出上述扫描规律下扫描镜的标称步进角/扫描角和成像点的标称位置(仅在区域扫描段计算成像点位置,其余时间段标称位置设为0).

图3 标称步进角与扫描角

图4 成像点标称位置
由于第1次区域扫描时扫描镜尚未进行恒星敏感,法线偏移参数未知,因此在第1次区域扫描时假定Δτx=Δτy=0,即不对法线偏移进行补偿,仅补偿姿态和轨道误差的影响;第2次区域扫描前已经通过恒星敏感对法线参数偏移进行估计,因此在第2次区域扫描中利用估计的参数对法线偏移进行补偿.
图5为卫星的姿态角变化曲线,在t=50 s时姿态尚未完全稳定,姿态偏差会对成像点位置产生一定的影响.
图6和图7分别给出了不加补偿和加入补偿后成像点的位置误差.两图对比可见,在第1次区域扫描过程中,补偿后的位置误差较补偿前有了明显提高,但由于没有对法线偏移信息进行估计和补偿,因此补偿后成像点位置仍然存在较明显的误差;在第2次区域扫描过程中已经对法线偏移信息进行估计和补偿,由图8可见,第2次区域扫描过程中成像点经度误差不到0.003°,纬度误差不到0.006°,较第1次区域扫描有了量级上的提高.

图5 卫星姿态角

图6 成像点位置误差(不加补偿)
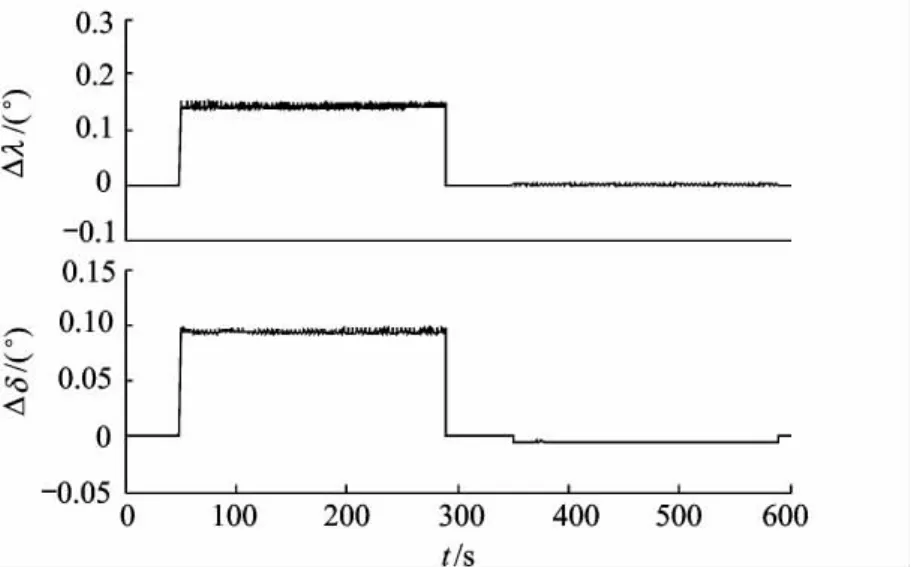
图7 成像点位置误差(加补偿)
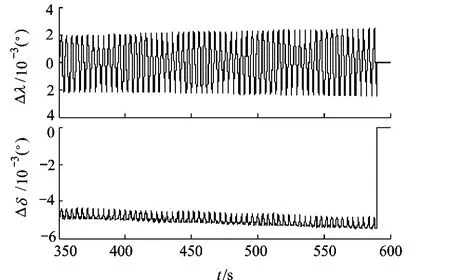
图8 成像点位置误差局部放大图(加补偿)
图9为相应的补偿角(仅在区域扫描模式进行补偿).整个区域扫描过程中补偿角均很小,同时由于补偿角与标称扫描角/步进角相关,因此尽管误差源大部分为慢变量,但补偿角仍体现出显著的快变特性.
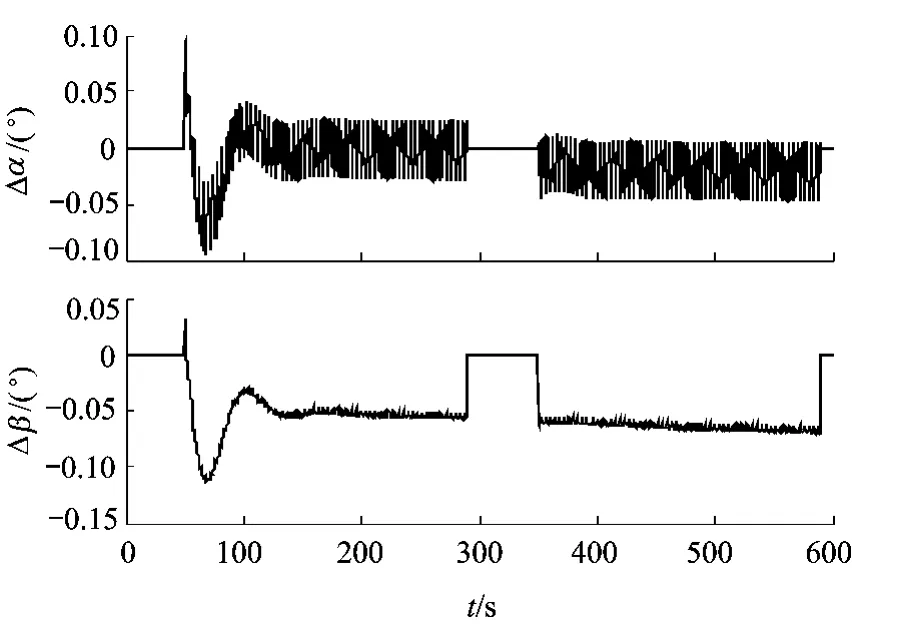
图9 扫描镜补偿角
6 结论
在考虑扫描镜法线偏移、卫星姿态偏差和轨道误差的情况下,对成像点地心经纬度位置有影响的误差可由9个独立的参数描述,其中8个角误差为小量误差参数,另一个参数为航天器的地心距.研究所得到的步进角/扫描角补偿量不仅与上述误差参数相关,也与标称扫描规律相关.
在法线偏移参数相对恒星敏感频率为慢变量以及卫星可相对惯性空间准确定姿的情况下,扫描镜进行一次恒星敏感即可对法线偏移信息作出准确的估计,并且在补偿算法中加以补偿.数值仿真结果表明,所研究的补偿方案和算法可显著提高成像点位置精度.
(References)
[1]陆风,许建民,张其松.风云二号气象卫星姿态和沿步进方向失配角参数对图像影响的模拟研究[J].应用气象学报,2001,12(4):393-398 Lu Feng,Xu Jianmin,Zhang Qisong.Impact study of attitude and pitch misalignment parameters on FY-2 image navigation with simulation method[J].Quarterly Journal of Applied Meteorology,2001,12(4):393-398(in Chinese)
[2]于哲峰,杨智春.扫描镜运动对三轴稳定卫星姿态影响研究[J].西北工业大学学报,2003,21(1):87-90
Yu Zhefeng,Yang Zhichun.Effects of scan mirror motion on the attitude of three-axis-stabilized geostationary satellite[J].Journal of Northwestern Polytechnical University,2003,21(1):87-90(in Chinese)
[3]刘蕊,王平,吕振铎.星上运动部件对气象卫星姿态影响的研究[J].中国空间科学技术,2005(6):1-7
Liu Rui,Wang Ping,Lü Zhenduo.Effects of spacecraft movable accessory on the attitude of meteorological satellite[J].Chinese Space Science and Technology,2005(6):1-7(in Chinese)
[4]于哲峰,杨智春.三轴稳定卫星扫描镜运动的偏差与补偿[J].西北工业大学学报,2003,21(4):465-468
Yu Zhefeng,Yang Zhichun.A simple and efficient compensation scheme for reducing scanning deviation of scan mirror of threeaxis-stabilized geostationary satellite[J].Journal of Northwestern Polytechnical University,2003,21(4):465-468(in Chinese)
[5]钱勇,南树军,刘利恒,等.基于模型预估方法补偿扫描镜运动对成像影响分析[J].弹箭与制导学报,2006,26(3):201-205
Qian Yong,Nan Shujun,Liu Liheng,et al.Influence analysis on imaging for scanning camera motion based on predicted model[J].Journal of Projectiles,Rockets,Missiles and Guidance,2006,26(3):201-205(in Chinese)
[6]Wang Zhigang,Chen Shilu,Li Qing.Scan mirror motion compensation technology for high accuracy satellite remote sebsor[C]//Wang Cheng,Zhong Shan,Wei Jiaolong.Second International Conference on Space Information Technology.Bellingham WA:SPIE,2007:1-7
[7]王志刚,袁建平,陈士橹.星载遥感器扫描运动控制补偿信号的生成与模拟[J].西北工业大学学报,2004,22(2):236-238
Wang Zhigang,Yuan Jianping,Chen Shilu.On determining compensation signals for scan motion control of satellite remote sensor[J].Journal of Northwestern Polytechnical University,2004,22(2):236-238(in Chinese)
[8]贾英宏,徐世杰.地球静止轨道卫星扫描镜运动补偿[J].北京航空航天大学学报,2007,33(8):873-877
Jia Yinghong,Xu Shijie.Scan mirror motion compensation of geostationary satellite[J].JournalofBeijing University of Aeronautics and Astronautics,2007,33(8):873-877(in Chinese)
[9]贾英宏,刘勇,徐世杰.航天器两自由度扫描镜图象运动补偿技术研究[J].航天控制,2008,26(1):32-37
Jia Yinghong,Liu Yong,Xu Shijie.Image motion compensation for a two-degree scan mirror of a spacecraft[J].Aerospace Control,2008,26(1):32-37(in Chinese)
[10]Kamel A A,Bhat M K P,Gamble D,et al.GOES I~ M image motion compensation system[R].AIAA-92-1107,1992
[11]Jung T S,Lee U S,Park S Y,et al.Design of an image motion compensation(IMC)algorithm for the communication,ocean,meteorological satellite(COMS)[C]//AIAA/AAS Astrodynamics Specialist Conference.Reston VA:American Institute of Aeronautics and Astronautics Inc,2006:930-940
[12]Hookman R A,Zurmehly G E,Hodgman N S.Scanning mirror design considerations for a geostationary spaceborne radiometer[C]//Scakaran G,James F S.Proceedings of SPIE 1693 Surveillance TechnologiesⅡ.Bellingham,WA:Society of Photo-Optical Instrumentation Engineers,1992:318-329
Imaging position error compensation of scan mirror for spacecraft
Jia Yinghong Xu Shijie Chen Tong
(School of Astronautics,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
An imaging position error compensation algorithm was proposed for a two-degree-of-freedom scan mirror of a geostationary spacecraft.The investigation aimed to eliminate the detecting area error on the earth surface by compensation of the mirror scanning angles.The formulas for calculating the geocentric longitude and latitude of the imaging point were deduced in which three types of errors,the mirror normal deviation,satellite attitude error and orbit error,were considered.Then the descriptions of the error sources were presented,and the effects of the errors on the imaging point position were analyzed.Based on the small quantity assumption of the angular errors,the compensation algorithms for east-west scanning angle and south-north stepping angle were proposed in explicit formulations.As the normal deviation was difficult to be measured accurately,an estimation algorithm for normal deviation was proposed based on the ability of accurate orientation determination of the optical axis in special operation mode and the long-period characteristic of the normal deviation.The simulation results indicate that the proposed compensation scheme and algorithm improve the imaging position accuracy evidently.
scanning;imaging;geostationary satellites;error compensation;error estimation
V 448.22+2
A
1001-5965(2012)02-0153-07
2010-10-18;< class="emphasis_bold">网络出版时间:
时间:2012-02-21 11:46;
CNKI:11-2625/V.20120221.1146.012
www.cnki.net/kcms/detail/11.2625.V.20120221.1146.012.html
贾英宏(1976-),男,河北阳原人,副教授,jia_yingh@yahoo.com.cn.
(编 辑:张 嵘)
