基于DE算法的共轴直升机模型辨识及精度分析

刘 鹏 蒙志君 武 哲

(北京航空航天大学 航空科学与工程学院，北京100191)

近年来，由于共轴直升机具有机身结构紧凑、适合在小场地起降、不存在尾桨事故等特点，共轴式双旋翼布局在轻型无人直升机中应用比较广泛.共轴直升机飞行动力学模型是开展操稳特性分析、飞行实时仿真、飞行控制系统设计等研究的基础［1］.

目前，关于单旋翼带尾桨直升机的建模研究非常多，也比较成熟［2－3］.然而由于共轴直升机特有的旋翼布局，引发了上下旋翼之间强烈的气动干扰，使得共轴式双旋翼空气动力学问题较单旋翼而言更加复杂和困难.国内外关于共轴式直升机的研究主要集中在双旋翼气动特性的理论分析和风洞试验方面［4－7］，而对共轴直升机飞行动力学建模的研究非常少.

本文运用一种基于微分进化算法的频域系统辨识方法得到了共轴直升机悬停状态下状态空间模型中的气动参数，并利用Cramer-Rao(CR)边界和不灵敏度的有关理论对辨识参数进行分析计算，说明辨识得到的参数具有较高的精度和可信度，辨识得到的模型的时域验证结果说明了辨识得到的模型是非常精确的.

1 机理模型建立

利用小扰动理论，得到了共轴直升机悬停状态下含有气动导数和控制导数的六自由度线性化状态空间模型如下［1，8］:

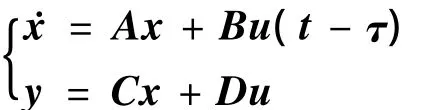
式中

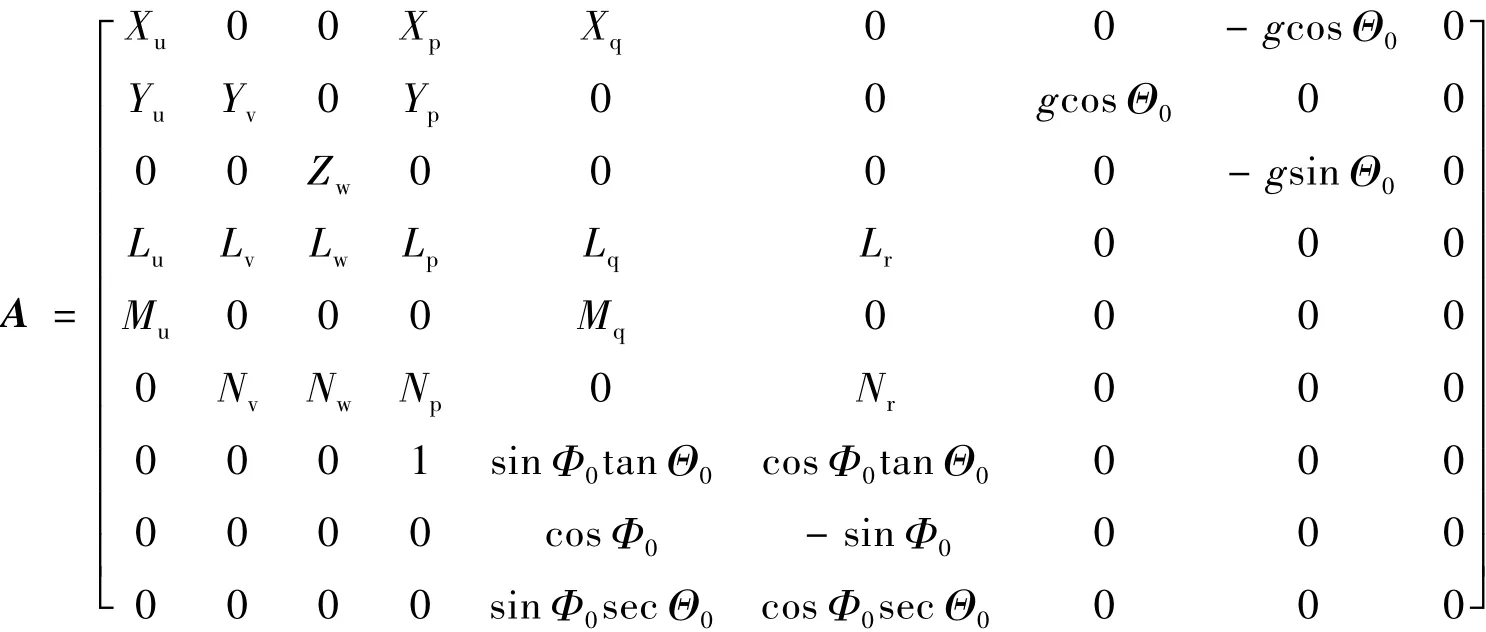
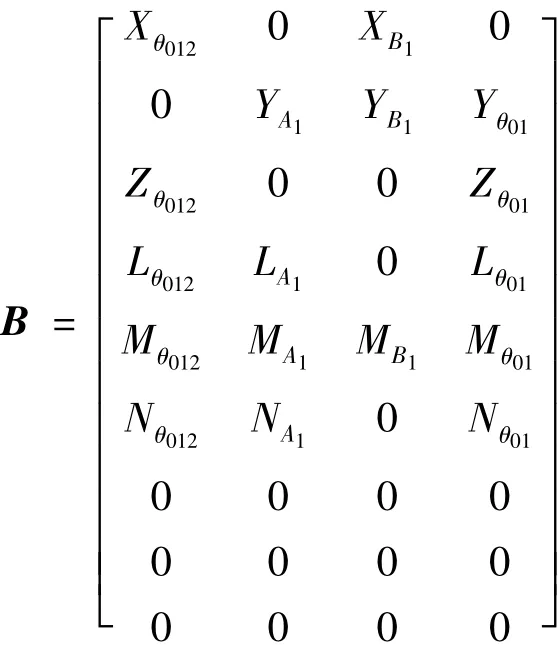
x表示状态向量;u表示控制输入向量;τ为控制量的延迟时间，具体如下:

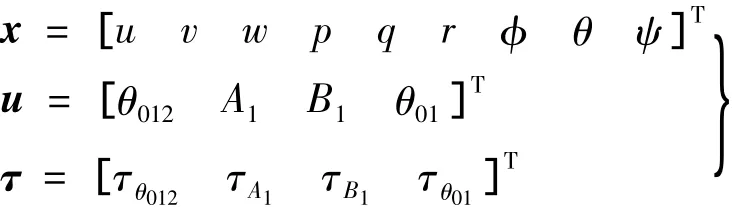
状态矩阵A由气动导数组成，控制矩阵B由控制输入导数组成，这些都是状态空间模型中的待辨参数，通过频域辨识的方法可以获得这些参数值的大小.

2 频域辨识方法及精度分析

2.1 频域辨识方法

运用拉氏变换，频率响应矩阵T(s)可以表示为状态空间方程系统矩阵的函数:

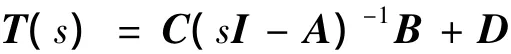
假定系统有nin个输入，nout个输出，可以写成如下多输入多输出传递函数矩阵的形式:

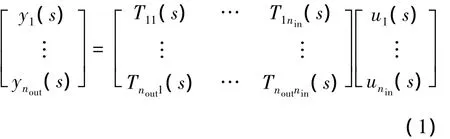
选取其中nTF对相干性较高 (相干函数值≥0.6)的频域响应Tc(ω)，将s=jω代入式(1)传递函数T(s)中，可以得到如下的以误差形式表示的状态空间方程辨识的代价函数:

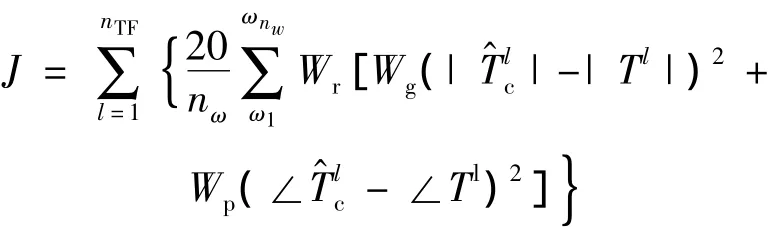
通常取代价函数J的平均值Jave=J/nTF进行计算，当平均代价函数满足Jave≤100时，将获得一个非常可靠的状态空间模型［9］.

将状态矩阵A、控制矩阵B和延迟时间τ中的d个待辨识参数用向量x来表示:

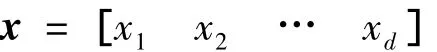
本文采用仿生智能计算方法中的微分进化算法来得到待辨参数的值.微分进化算法是一种基于群体进化的仿生智能计算方法，通过种群内个体间的合作与竞争来实现对优化问题的求解.微分进化算法的基本操作包括变异、交叉和选择3种操作［10］.

设种群规模Np可行解空间维数为d，用x(t)=［x1x2… xd］表示第t迭代时刻的解向量，微分进化算法运行过程的步骤［11］如下:

1)随机初始化.解空间随机产生初始种群:

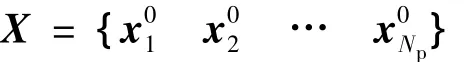
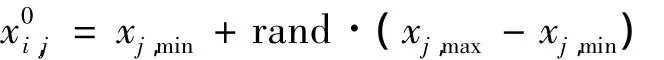
2)变异操作.变异个体的生成过程中用到了父代种群中多个个体的线性组合，最基本的变异成分是父代个体的差分向量.对父代种群中任意个体，经如下变异操作生成变异个体

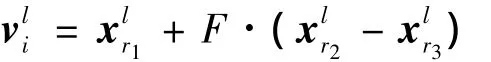
图1 微分进化算法的变异操作

式中，randb是 ［0，1］间的随机数;rj是在［1，d］间随机选择的整数;交叉常量CR是在［0，1］间的常数，微分进化算法的变异操作过程如图2所示.

4)选择操作.微分进化算法的选择操作是一种“贪婪”选择模式，当且仅当新的向量个体的适应度值比目标个体的适应度值更好时，才会被种群接受为.选择操作由下式描述:

微分进化算法的选择操作使得子代个体总是优于或等于父代个体，从而使种群始终向最优解的方向进化.

2.2 辨识参数精度分析

参数精度理论分析的基础是Cramer-Rao不等式:σi≥Pi.CR边界值Pi是多次重复试验所得参数估计的标准差σi的最小值，各辨识参数的CR边界值是改进模型结构的关键准则.如果某参数的CR边界值过大，则表明参数辨识结果可信度很低，意味着该参数应当从模型结构中去除或进行调整改进.

对于个别的CR边界值超过要求的辨识参数，辨识得到的模型也是可以接受的［9］.

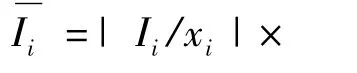
3 状态空间模型辨识

3.1 飞行扫频试验设计

飞行试验数据必须充分包含动力学模型的丰富信息，故采用扫频试验获得飞行数据，即通过操控手逐渐增加输入的频率［13］.

通过大量飞行扫频试验总结，共轴直升机和单旋翼带尾桨直升机做辨识试验的主要区别在于共轴直升机扫频时操纵量输入不能太大，否则会造成上下旋翼打桨，输入量幅值一般应控制在±10%行程内.

横向通道扫频数据如图3所示，从图中可看到，横向扫频输入A1和横滚角速度输出p有很高的一致性，这为系统辨识提供了很好的频谱特性.

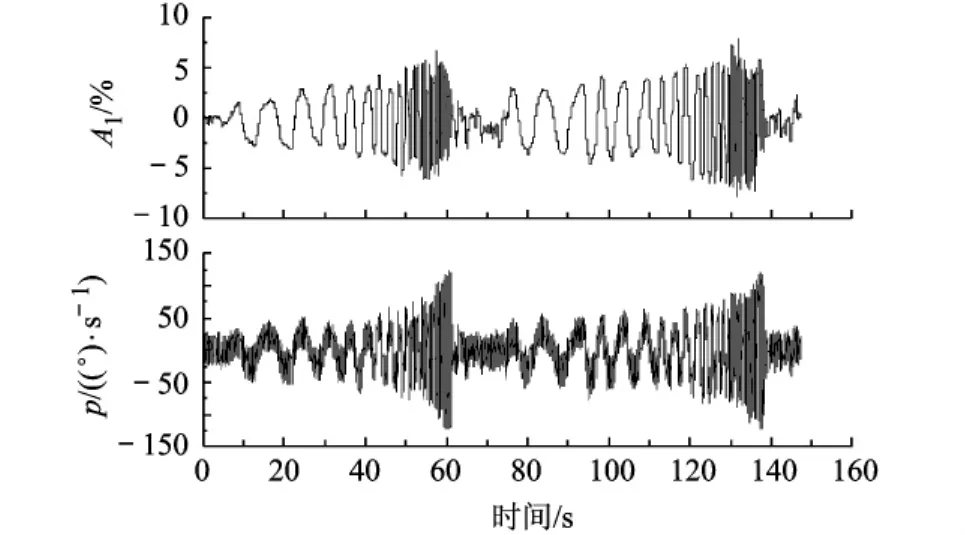
图3 横向通道扫频数据

3.2 状态空间模型辨识

在获得了满足要求的辨识数据后，用偏相干分析去除其他通道的耦合效应，通过输入输出信号的功率谱密度计算得到包含共轴直升机动力学模型耦合特性的非参数频率响应，如图4所示.

利用前面介绍的微分进化算法来搜索最小代价函数.表1列出了悬停状态下辨识得到的模型的代价函数，从表中可看出，频率响应的代价函数都小于标准值，并且平均的代价函数值低于100，说明辨识得到的模型与试验数据匹配得很好.

表1 辨识过程传递函数的代价函数值J

图4比较了辨识得到的模型与试验数据计算得到的主通道频率响应，可以看出模型与试验数据取得了很好的一致性.

那些具有较大Cramer-Rao边界值和不灵敏度值的参数在辨识过程中从待辨模型中去除.表2列出了参数辨识的结果、Cramer-Rao边界和不灵敏度值，结果都满足辨识要求，说明辨识参数的精度比较高.

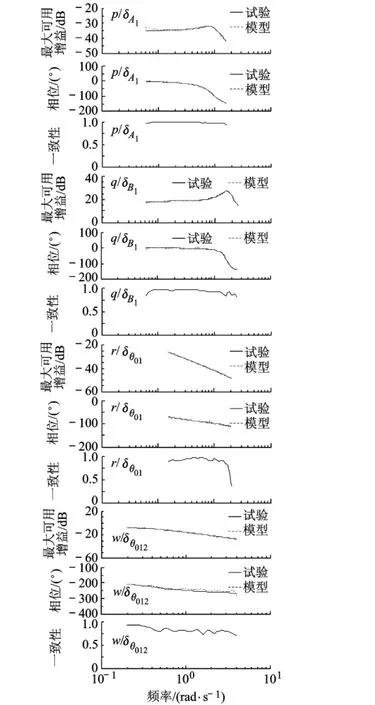
图4 飞行数据和辨识模型的频率响应比较

表2 共轴直升机悬停状态下辨识结果

3.3 模型验证

把一组用于模型验证的Doublet输入信号［13］作为辨识得到的共轴直升机状态空间模型的输入值，比较辨识得到的模型的预测输出和实际的飞行数据.航向通道的模型验证结果如图5所示，从图中可以看出，实际飞行数据和辨识模型的吻合度是比较理想的，说明此辨识模型的结果的准确性是比较高的.

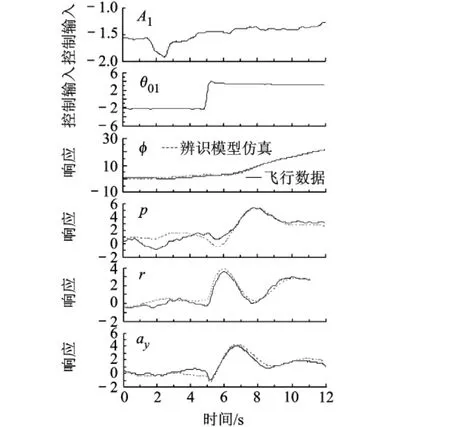
图5 航向通道模型验证

4 结论

通过以上论述，可以得出以下结论:①通过大量飞行扫频试验，总结得到共轴直升机和单旋翼带尾桨直升机辨识试验主要的区别在于操纵手在扫频时操纵量输入不能太大，否则会造成上下旋翼打桨，输入量幅值一般应控制在±10%行程内;②在辨识过程中，将微分进化算法应用到搜索代价函数的最小值中，通过拟合由试验数据得到的频率响应曲线，得到了共轴直升机状态空间模型中的待辨参数;③利用Crame-Rao边界和不灵敏度的有关理论对辨识参数结果进行分析，辨识参数的Cramer-Rao边界和不灵敏度值都满足辨识要求，说明辨识参数的精度比较高;④通过时域交叉验证，说明了基于该频域辨识方法建立的共轴直升机状态空间模型的精确性和有效性，可以在该状态下以此模型进行自主飞行控制器设计.

References)

［1］周国仪.共轴式直升机飞行动力学建模及数值模拟［D］.北京:北京航空航天大学航空科学与工程学院，2003

Zhou Guoyi.Modeling and numerical simulation of the dynamics of coaxial helicopter［D］.Beijing:School of Aeronautic Science and Engineering，BeiJing University of Aeronautics and Astronautics，2003(in Chines)

［2］Mettler B.Modeling small-scale unmanned rotorcraft for advanced flight control design［D］.Pittsburgh:The Robotics Institute，Carnegie Mellon University，2001:43 －66

［3］孙涛，宋彦国.一种无人直升机飞行力学模型辨识方法研究 ［J］.航空学报，2007，28(增刊):14－18

Sun Tao，Song Yanguo.Study on a method for unmanned helicopter flight dynamics model identification ［J］.Acta Aeronautica et Astronautica Sinica，2005，28(Supplement):14－18(in Chinese)

［4］Coleman C P.A survey of theoretical and experimental of coaxial rotor aerodynamic research［C］//Cansdale J T.19th European Rotorcraft Forum.Como:European Rotorcraft Forum，1993:131－135

［5］Coleman C P.Aerodynamics feasures of a coaxial rotor helicopter［C］//Cansdale J T.17th European Rotorcraft Forum.Berlin:European Rotorcraft Forum，1991:66－71

［6］邓彦敏，陶然，胡继忠.共轴式直升机上下旋翼之间气动干扰的风洞实验研究［J］.航空学报，2003，24:10－14

Deng Yanmin，Tao Ran，Hu Jizhong.Experimental investigation of the aerodynamic interaction between upper and lower rotors of a coaxial helicopter［J］.Acta Aeronautica et Astronautica Sinica，2003，24:10－14(in Chinese)

［7］周国仪，胡继忠，曹义华.共轴式直升机双旋翼载荷计算模型研究［J］.航空动力学报，2003:343－347

Zhou Guoyi，Hu Jizhong，Cao Yihua.Mathematical model for twin rotor loads of a coaxial helicopter［J］.Journal of Aerospace Power，2003:343－347(in Chinese)

［8］高正，陈仁良.直升机飞行动力学［M］.北京:科学出版社，2003:1－4

Gao Zheng，Chen Renliang.Helicopter aerodynamics［M］.Beijing:Science Press，2003:1－4(in Chinese)

［9］Tischler M B，Remple R K.Aircraft and rotorcraft system identification:engineering methods with flight test examples［M］.USA:AIAA，2006

［10］Storn R，Price K.Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces［J］.Global Optim，1997，11:341－359

［11］段海滨，张祥银.仿生智能计算 ［M］.北京:科学出版社，2011:107－114

Duan Haibin， Zhang Xiangyin. Bio-inspired computing［M］.Beijing:Science Press，2011:107－114(in Chinese)

［12］Maine R E，Iliff K W.The theory and practice of estimating the accuracy of dynamic flight-determined coeffieients［J］.NASARP-1077，1981

［13］Ivler C M，Tischler M B.Control system development and flight test experience with the MQ-8B fire scout vertical take-off unmanned aerial vehicle［C］//Downs J.Prentice R，Dalzell s，et al.Journal of the American Helicopter Society.Virgina:The american Helicopter Society Inter national Inc，2007:1－27