交替LU分裂算法及其在CFD中的应用

相 倩 吴颂平

(北京航空航天大学 航空科学与工程学院，北京100191)

徐 悦

(中国航空研究院 航空数值模拟技术研究应用中心，北京100012)

随着CFD(Computational Fluid Dynamics)模拟能力的提高，计算中需要求解的方程组的规模也急剧增加.快速求解大型方程组已经成为CFD计算的瓶颈之一［1］.迭代算法是求解大型方程组的有效方法，其收敛速度依赖于方程组系数矩阵的性质.针对超声速流动离散方程组系数矩阵往往是本质正定的这一特点，本文提出了一种迭代算法，称为交替LU分裂 (ALUS，Alternating Lower-Upper Splitting)算法.该算法计算量小，易于实现，且具有很好的鲁棒性，可大大节省计算时间.

1 迭代算法

常用的迭代算法分为两类.一类是基于系数矩阵分裂的古典迭代方法，例如Jacobi方法，Gauss-Seidel方法，松弛法 (SOR，Successive O-ver Relaxation)等.其中交替方向算法因其简单容易实现，在实际计算中有着广泛的应用［2］.近些年逐步发展起来的HSS(Hermitian and skew-Hermitian Splitting)方法［3］和 PSS(Positive definite and skew-Hermitian Splitting)方法［4］及其扩展算法也可以看作是广义的交替方向算法，具体参见文献［5］.另一类算法是基于变分极值原理的迭代算法，其中最具代表性的有适用于对称正定系统的共轭梯度法 (CG，Conjugate Gradient)以及适用于非对称正定的广义极小残量法 (GMRES，Generalized Minimal Residual).

1.1 交替方向算法

设矩阵A∈Cn×n，考虑线性方程组

若A可以分解成A=Q+S，则迭代算法

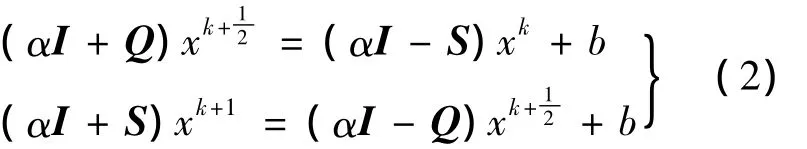
称为交替方向算法.该算法亦可以写成

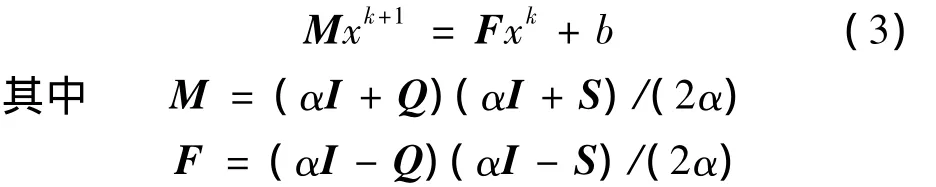
并且A=M－F.由式 (3)可知，矩阵M可以看成是一个预处理算子.一个好的预处理算子M应该构造简单易于求逆，并且谱半径ρ(M－1F)应该尽可能小.

对于交替方向算法式 (2)，有以下定理成立.

定理1 对任意的正实数α＞0，若αI+Q和αI+S都是可逆矩阵，迭代过程式 (2)收敛的充要条件是:ρ［(αI－ Q)(αI+Q)－1(αI－ S)·(αI+S)－1］＜1，并且倘若迭代过程式 (2)收敛，则必收敛到方程组 (1)的解.

1.2 HSS算法和PSS算法

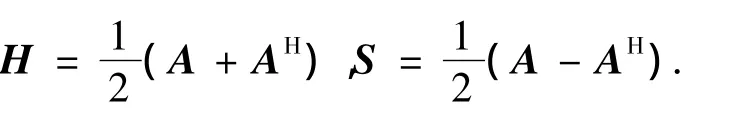
若D、L和U分别代表矩阵A的对角线、严格下三角和严格上三角部分，则A还可以分解成下三角矩阵和反Hermite矩阵之和，A=P+，其中，P=D+L+UH，=U － UH.

引理1 设矩阵 P∈Cn×n.如果 P+PH正定，则对任意的实数α＞0，当αI+P可逆时，‖ (αI－P)(αI+P)－1‖2＜1.

引理2 设矩阵S∈Cn×n是反Hermite矩阵，则‖ (αI－S)(αI+S)－1‖2=1，∀α ＞0.

定理2 若H+HH正定，则对任意实数α＞0，迭代算法

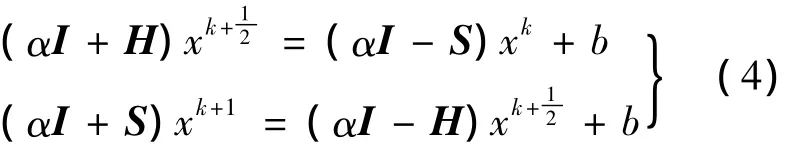
是收敛的，则称为HSS迭代算法.

定理3 若P+PH正定，则对任意实数α＞0，迭代算法

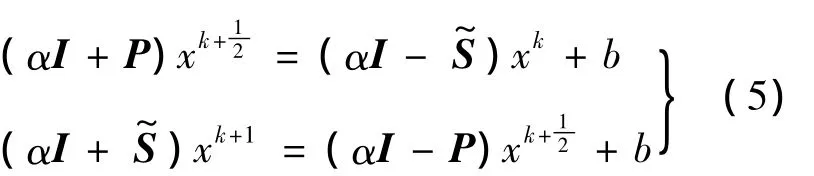
是收敛的，称其为PSS迭代算法.

共轭斜量法是求解对称正定线性方程组的有效方法，消去法是求解下三角线性方程组的有效方法.文献［6］充分利用反对称矩阵S的特点，给出了快速求解带位移的反对称问题 (αI+S)y=的SSS(Solving a Shifted Skew-Symmetric Systems)算法.将这些求解方法结合起来，使得HSS迭代算法和PSS迭代算法成为有效的广义交替方向迭代算法［7－8］.尽管如此，HSS算法和PSS算法仍然存在很多问题，例如:当矩阵A的阶数为奇数时，反对称矩阵S是奇异的，而参数α的取值通常比较小，这将导致计算不稳定;无论是HSS还是PSS方法都需要求解带位移的反对称方程组，但上述SSS算法比较复杂计算缓慢.为此，本文提出了交替LU分裂算法.

1.3 ALUS算法

将对角矩阵D分解成D1，D2两部分，则矩阵A可分裂成下三角矩阵=D1+L与上三角矩阵之和，于是由引理1，可得到以下结论.

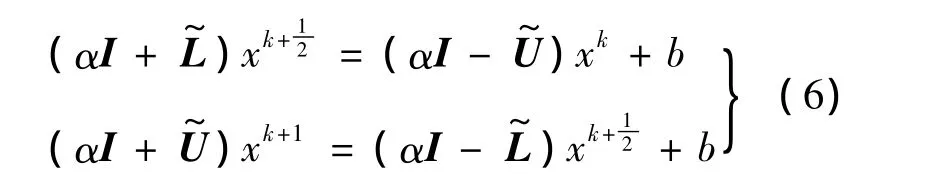
是收敛的，本文称为交替LU分裂算法.

按照式 (3)，记

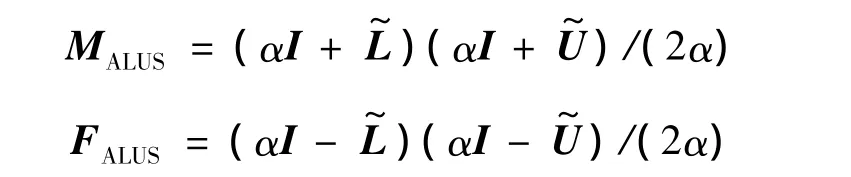
则有

2 数值实验

计算效率以及迭代矩阵的谱半径是衡量迭代算法优劣的重要标准.通过以下算例对本文的ALUS算法进行评估.

2.1 线性问题

在区域D={0≤x，y≤1}上考虑边值问题

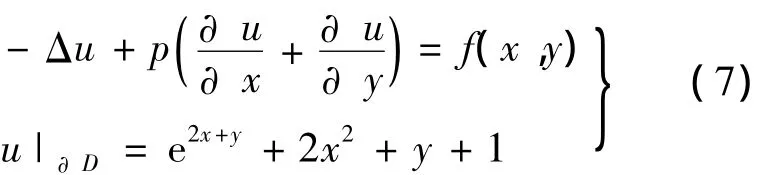
其中，p＜0;f(x，y)=(3p－5)e2x+y+4xp+p－4，该问题的解析解为u=e2x+y+2x2+y+1.

取自然数N，令h=1/N，采用均匀网格Δx=Δy=h进行离散区域D，考虑式 (7)的差分近似

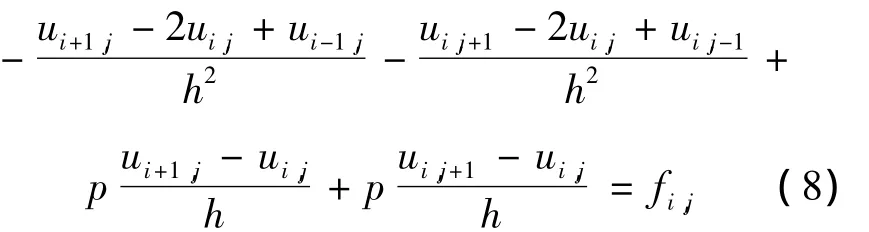
用ALUS算法求解方程组 (8)，初始近似取零向量，迭代的收敛标准是残差小于10－6.

参数p决定了线性方程组的系数矩阵性质.|p|越小，系数矩阵越接近对称矩阵;|p|越大，系数矩阵的非对称性越强.参数N决定了系数矩阵的规模.参数α决定了迭代矩阵的谱分布，影响了迭代的收敛速度，记能使迭代步数最少的α值为α*，通过数值实验，表1给出了不同p和N下α*的取值.

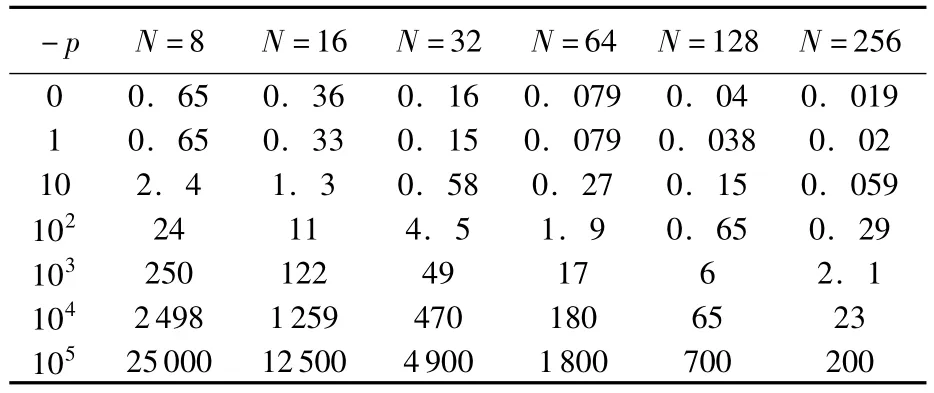
表1 α 的取值

尽管不能给出α*的精确表达式，但从表1中可以看出，当|p|≥10时，α*与|p|近似成正比，与N成反比，可用经验公式表示为α*≈2|p|/N，如图1所示.

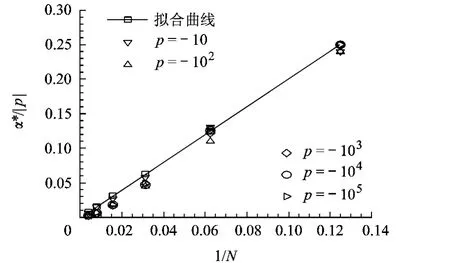
图1 α*与p、N关系图

表2和表3给出了不同p、N和α下，迭代矩阵的谱半径ρ(M－1ALUSFALUS).由表2和表3可以看到，参数α可以在很大范围内取值，这表明ALUS算法具有很好的鲁棒性.表4给出了p=－1，N=100时，GMRES算法，HSS算法、PSS算法以及ALUS算法收敛所需的CPU时间及迭代步数.由表4可知，本文的新算法，计算所需CPU时间较小，收敛快是一种高效迭代算法.

表2 p=－10，N=32时，迭代矩阵谱半径

表3 p=－103，N=32时，迭代矩阵谱半径

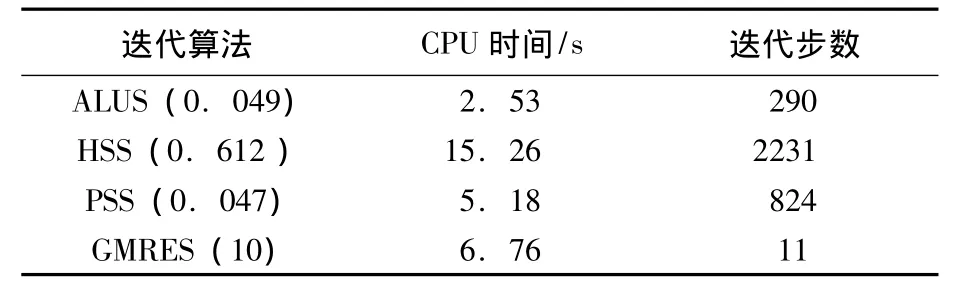
表4 不同迭代算法的比较

2.2 二维超声速圆柱绕流

将ALUS算法应用于超音速圆柱绕流的CFD计算中.算例中，来流马赫数Ma=8，雷诺数Re=1.59 ×105.

在计算坐标系下，二维Navier-Stokes方程的形式可以表示为

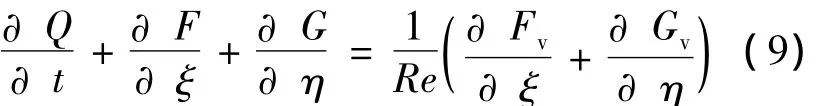
式中的粘性通量采用中心差分，无粘通量采用Harten-Yee的TVD(Total Variation Diminishing)格式，时间推进则采用了新的ALUS算法.计算网格为结构网格，大小为100×80.迭代的收敛标准是残差小于10－8.

表5给出了不同参数α下，ALUS算法的迭代步数以及CPU计算时间，并与经典的LU-SGS(Lower-Upper Symmeffic Gauss-seidel)算法进行对比.可以看出，本文的ALUS算法较经典的LU-SGS算法收敛的更快，计算时间甚至可以节约20%以上;而且α在很广的范围内，迭代都是收敛的.

为了进一步分析LU分裂算法的计算效率，图2给出了 CFL值分别为1.3以及2.4时，ALUS算法以及LU-SGS算法的收敛史.

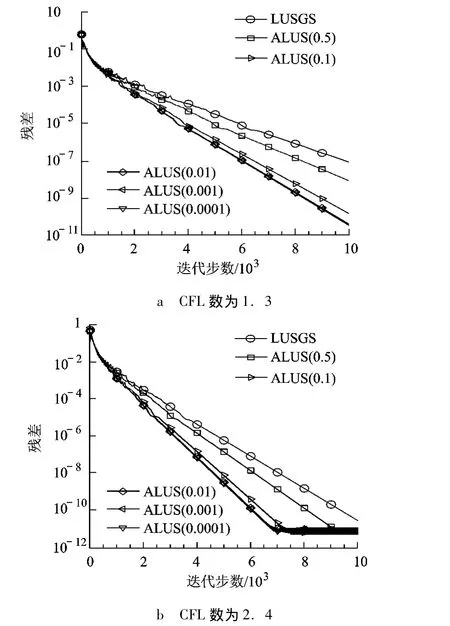
图2 不同CFL数下的收敛史

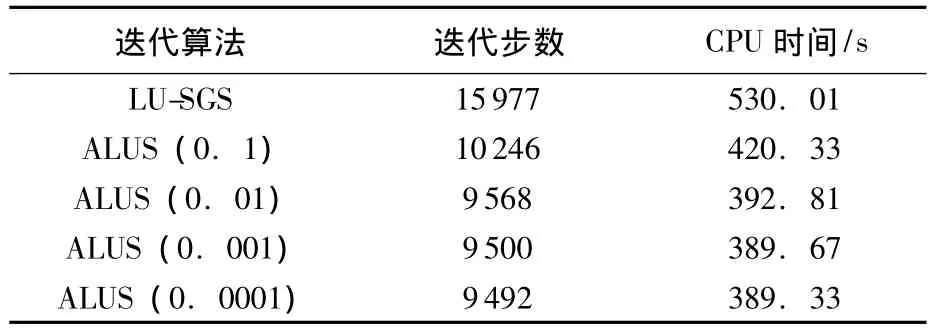
表5ALUS算法与LU-SGS算法的比较

数值实验的结果表明，本文给出的ALUS算法是一种效率高、鲁棒性好的迭代算法，可用于CFD的计算.

3 结论

对于求解大型方程组的交替方向算法，提出了新的ALUS算法.该算法在每步迭代中只需要求解两个三角方程组，计算量很小.与其他同类迭代算法相比，收敛得更快，因此是一种高效的迭代算法.数值实验还表明，算法中的参数α在很广的范围内取值，迭代均能收敛，可见新算法鲁棒性很好.二维超声速圆柱绕流的算例则表明，ALUS算法可用于CFD计算.

References)

［1］李良.大型线性方程组求解技术及在计算电磁学中的应用研究［D］.成都:电子科技大学数学科学学院，2009

Li Liang.Study of solutions to large linear systems with applications in computational electromagnetic［D］.Chengdu:School of Mathematical，University of Electronic Science and Technology，Jr of China，2009(in Chinese)

［2］Peaceman D W，Rachford H H，Jr.The numerical solution of parabolic and elliptic differential equations［J］.J Soc Indust and Appl Math，1955，3(1):28－41

［3］Bai Z Z，Golub G H，Nq M K.Hermitian andskew-Hermitian splitting methods for non-Hermitian positive definite linear systems［J］.J Matrix Anal and Appl，2003，24(3):603 －626

［4］Bai Z Z，Golub G H，Lu L Z，et al.Block triangular and skew-Hermitian splitting methods forpositive-definite linear systems［J］.J Sci Comput，2006，26(3):844 －863

［5］蒋尔雄.矩阵计算［M］.北京:科学出版社，2008:104－120

Jiang Erxiong.Matrix computations［M］.Beijing:Science Press，2008:104－120(in Chinesec)

［6］Jiang Erxiong.Algorithm for solving a shifted skew-symmetric linear system［J］.Front Math China，2007，2(2):227 －242

［7］Benzi M，Guo X P.A dimensional split preconditioner for Stokes and linearized Navier-Stokes equations［J］.Applied Numerical Mathematics，2011，61(1):66 －76

［8］Bai Z Z，Benzi M，Chen F.On preconditioned MHSS iteration methods forcomplex symmetric linear systems［J］.Numer Algorithms，2011，56(2):297 －317