守恒律方程的导数人工压缩法

董海涛 刘福军 韩 冲

(北京航空航天大学 航空科学与工程学院，北京100191)

流体力学方程组解的间断性在早期是一个主要难点，所有二阶以上的经典格式 (如 Lax-Wendroff格式)在激波等间断处会不可避免地出现伪振荡.之后，由于TVD(Total Variation Diminishing)判据及限制器技术的出现，产生了一批无振荡高精度格式，如TVD，ENO(Essentially Non-oscillatory)，NND(Non-Oscillatory and Non-free-parameter Dissipation)，无振荡紧致格式、熵条件格式等，统称为高分辨率格式，对激波的模拟取得了较好结果.许多复杂流动问题，流动参数变化剧烈，除可能存在激波间断外，还有带极值点的涡结构等，尤其对低速问题 (定常)没有激波间断，更多的 (高雷诺数)是极值点.而现有高分辨率格式若严格要求无振荡，则都存在极值点精度退化问题，为了更好地模拟复杂流动问题，须考虑提高极值点处的精度.目前，对这个问题的研究还较少，本文提出的导数人工压缩，就是为了解决20世纪80年代以来这些高阶格式在极值点降阶的问题，以提高对极值点的分辨率.本文先进行了导数人工压缩方法的推导，并构造了人工压缩和导数人工压缩结合的混合格式，然后用单个标量方程的多极值间断初值问题和Shu-Osher激波管算例进行了数值验证，极值点处的精度得到较好的改善.

1 导数人工压缩法的思想和推导

1977年文献 ［1］提出人工压缩方法并在1983年用于Harten-TVD［2］格式，以提高接触间断分辨率，本文受此启发，获得了导数人工压缩方法构造思路.考虑守恒律方程初值问题

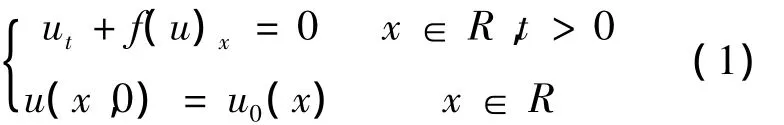
1.1 Harten的人工压缩法

Harten的原始二阶TVD格式为

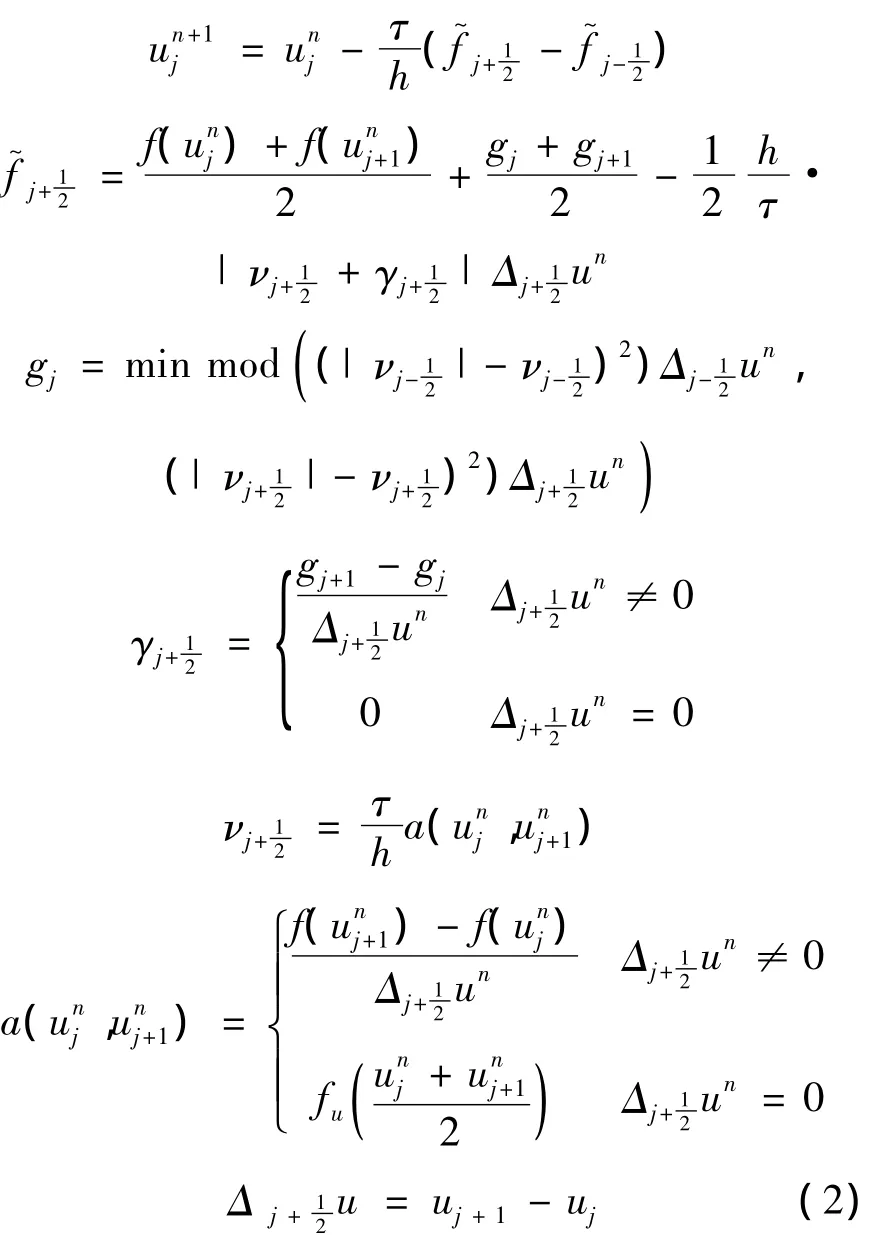
其中绝对值号 Harten原格式为 Q(ν)［1］，因其增加数值粘性，并且已有严格熵条件方法［3］，本文忽略这种近似熵修正.

人工压缩法既给原通量加一具有收缩特征场的小通量 (人工压缩通量)，使特征线平行的线性 (退化)场变成非线性压缩场，从而抑制数值耗散，达到提高 (接触)间断分辨率的目的(不同于提高精度).

Harten人工压缩通量的构造方法为:通过引入人工压缩通量增加间断左端的特征速度，减小间断右端的特征速度，从而把原特征场变成压缩场［1］，将原格式的gj按如下公式替换，即可得到带人工压缩的Harten-TVD格式

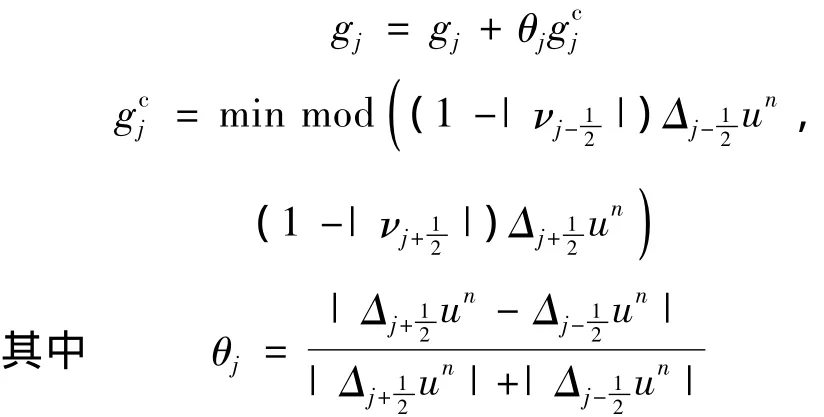
1.2 导数人工压缩法

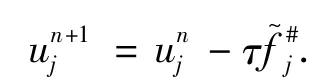
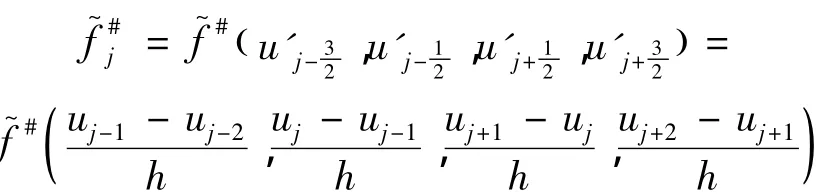
值得注意的是这个格式是非守恒形式，只能用在原函数连续的地方，不能用于间断处.即使线性方程也不能在间断处用导数方程，因为间断的导数为无穷，这种情况使用数值格式误差非常大.最后综合起来，数值方法用到两种途径推导的格式，需要研究一下如何匹配好.

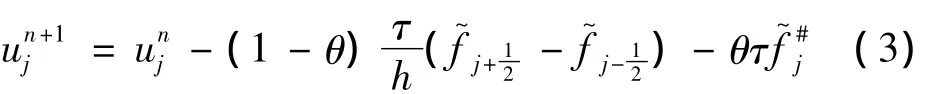
1.3 导数人工压缩法守恒修正

在计算中发现，对于非线性场有时甚至线性场，非守恒部分常常导致数值解的间断有明显相位误差.如，用于激波管问题中时发现激波位置计算得不准确，非守恒通量权数θ越大，激波位置偏差越大.因此，本文又进行了守恒修正，用守恒格式的一阶部分的主要项代替非守恒格式的一阶部分的主要项，这样导数方程的数值通量的非守恒部分是个小量，是近似守恒.将数值通量分为主要部分与小量部分

其中

式 (3)其余记号同式 (2)，守恒修正后格式为

1.4 方程组的导数人工压缩

导数人工压缩格式可按特征方向单个化的方法推广于双曲型守恒律方程组

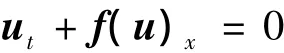
方程组的导数人工压缩格式为

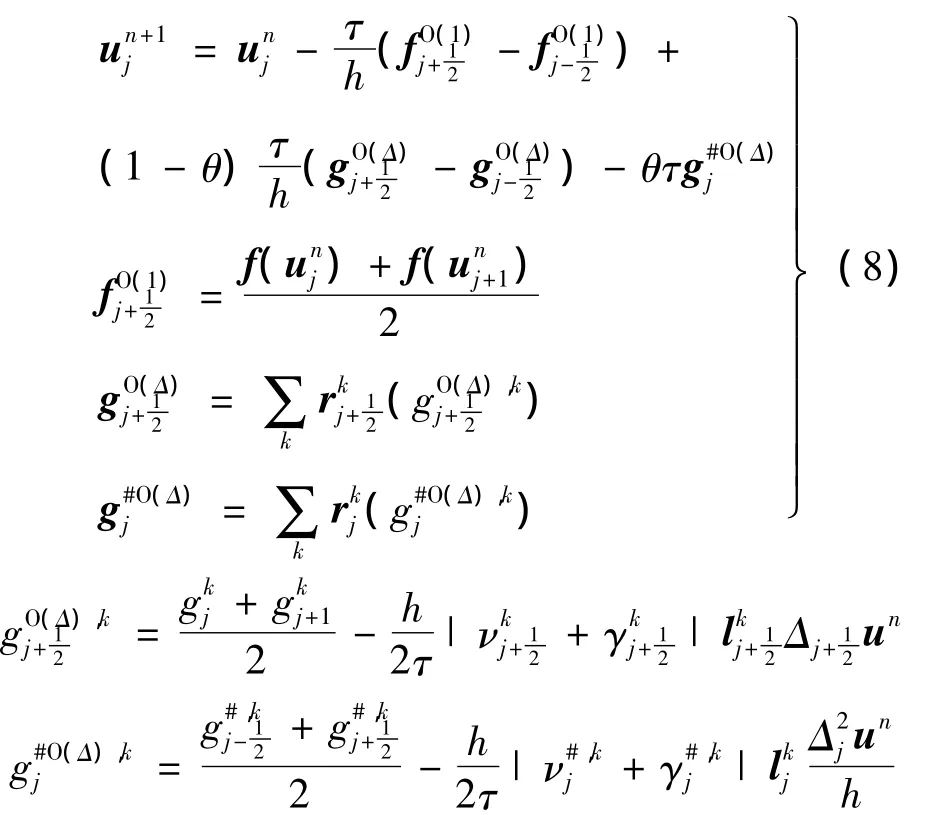
2 算例验证

单个方程算例取线性通量f(u)=u.方程组算例为一维完全气体Euler方程

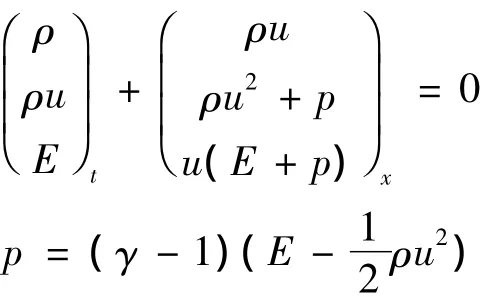
算例1 极值间断算例

初值条件

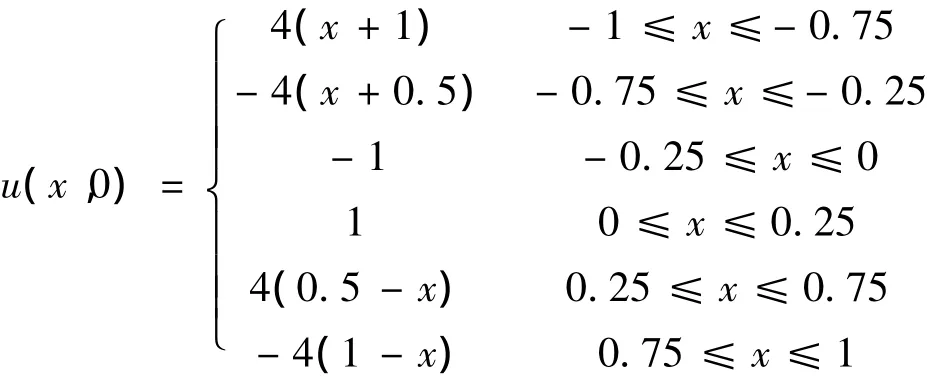
计算时间为2，计算网格为100，CFL数为0.5，格式混合参数θ=0.12.分别采用Harten-TVD格式 (原格式)、带人工压缩的Harten-TVD格式 (人工压缩)和本文新格式 (导数人工压缩)进行计算，结果如图1所示.可以看出，原格式在间断处和极值点处抹光都很厉害，人工压缩在极值点处和间断处相对于原格式都有明显改善.导数人工压缩在间断处同人工压缩格式重合，在极值点处导数人工压缩比人工压缩格式更接近于精确解.

图1 单个方程间断问题的数值解

算例2 极值间断相邻算例［4］

初值条件

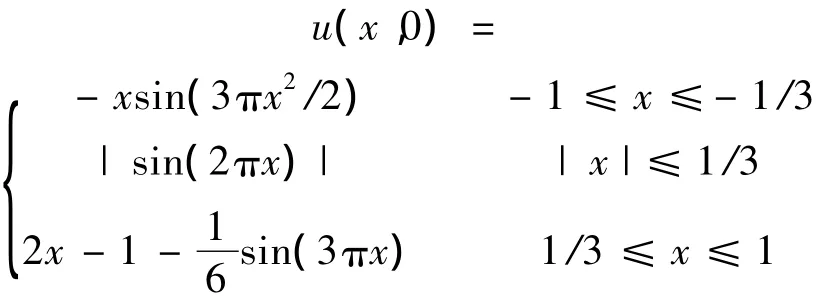
计算时间为0.5，计算网格为100，CFL数为0.3，格式混合参数θ=0.4.所采用的格式同上，在图2中也可以看出人工压缩和导数人工压缩在间断和极值点处的作用.

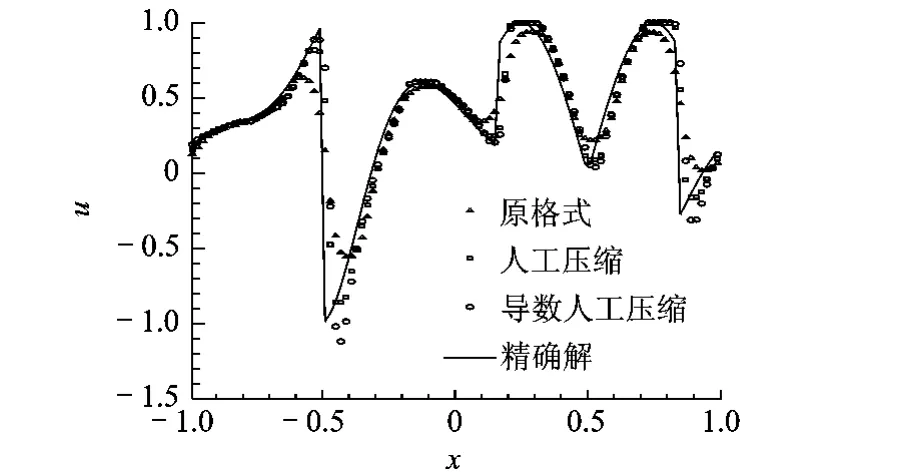
图2 单个方程极值间断相邻的数值解

算例3 多极值算例

初值条件

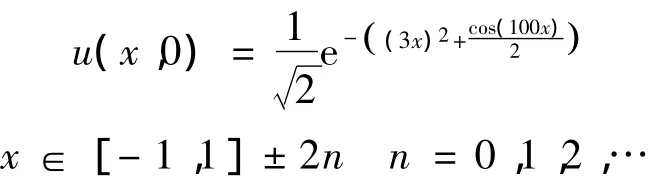
计算时间为2，计算网格260，CFL数为0.3，仍然采用上述3种格式，格式混合参数θ取0.07.计算结果如图3、图4所示.此算例显示原格式完全失去对脉动波的分辨能力，人工压缩可以分辨出脉动但有较大误差，而本文提出的导数人工压缩则可以很小的误差分辨脉动.

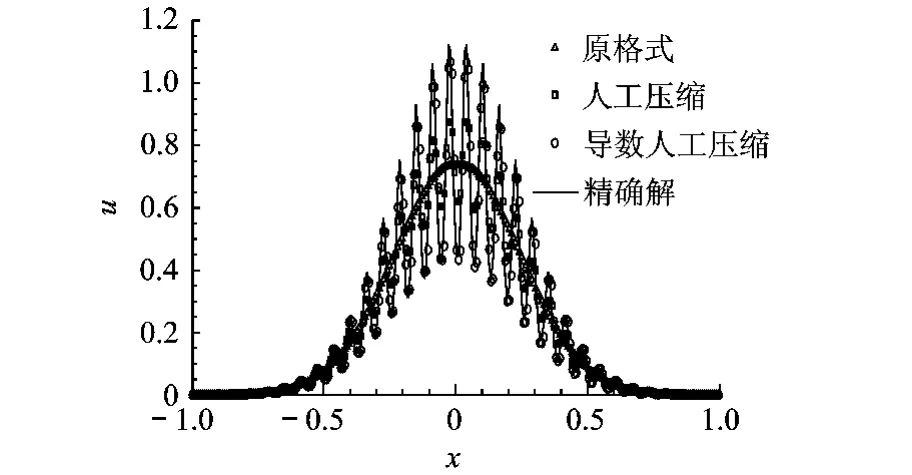
图3 单个方程多极值问题的数值解

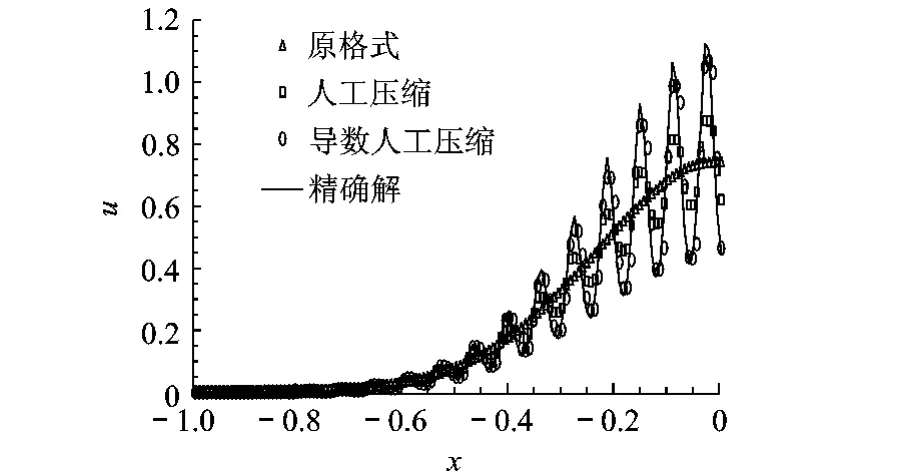
图4 单个方程多极值问题的数值解局部放大图

算例4 振荡激波管算例

文献 ［5］中构造了初始值一端有密度脉动的激波管算例，初值条件为

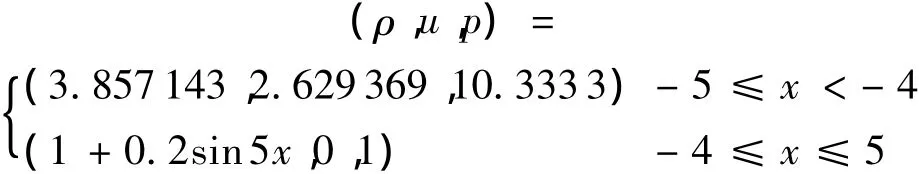
此算例没有精确解，本文采用10000网格上的TVD格式的解作为精确解，用400网格上的计算结果进行比较.CFL数为0.8，计算时间为1.8，格式混合参数θ取0.04，计算结果如图5所示.

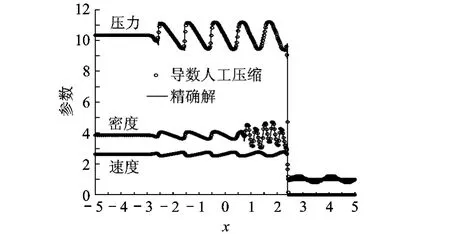
图5 导数人工压缩计算结果与精确解的比较

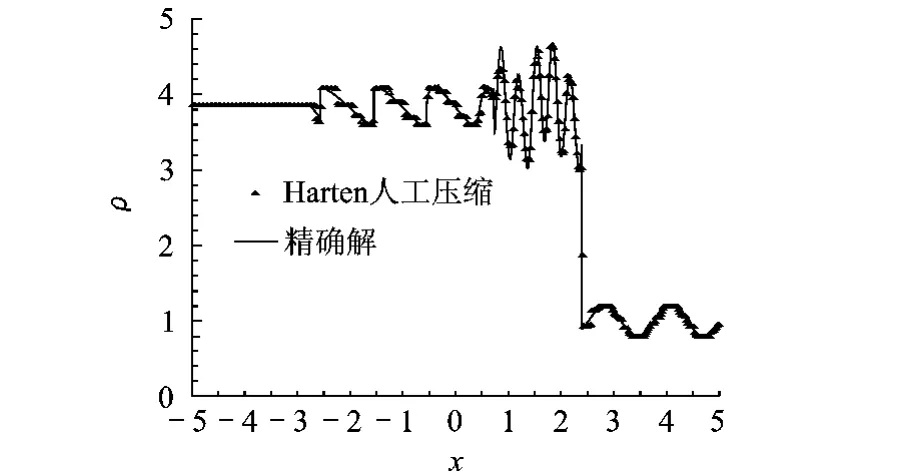
图6 Harten人工压缩与精确解的比较

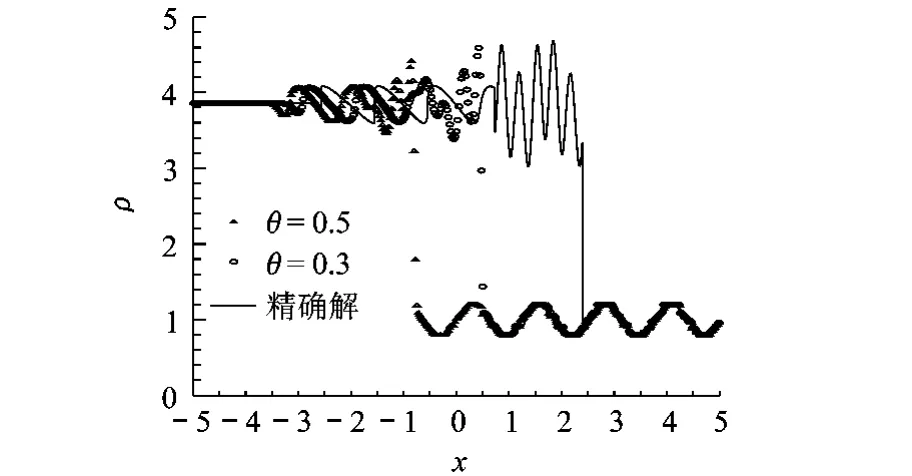
图7 未做守恒修正时的计算结果与精确解的比较

为显示新方法的优点，以密度图为例，对不同格式进行对比，同时显示计算过程发现的问题.图6显示的是 Harten人工压缩过压缩造成的阶梯现象，本文按照文献［6］的方法，只在线性场中进行压缩明显改善了这个现象.图7是格式 (3)计算的Shu-Osher算例密度图，因格式的非守恒性造成的激波位置的偏移很明显，可以看出，随着非守恒数值通量 f～#的增大，激波位置的偏移越大来越大，这种偏移在使用守恒修正(式 (4)～式 (6))后消除.从图8、图9可以看出，采用人工压缩格式的解在极值处比原始格式要好得多，导数人工压缩格式在极值处的解又比人工压缩的格式有明显改善.导数人工压缩格式在极值点不再受TVD或保单调限制，但仍受保凸性限制，故仍然严格满足无振荡条件.

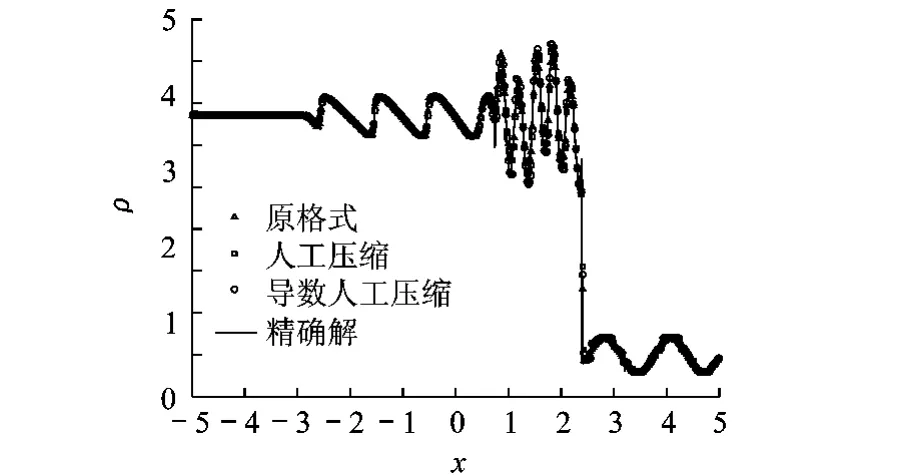
图8 三种格式的密度图比较

2.4 格式混合参数θ的选取

由于本文构造的新格式压缩性较大，作为导数人工压缩权重的混合参数θ都很小，综合几个算例来看都在0.1附近，算例2中取值为0.4，注意到精确解中有两处同时存在间断和极值，为了抵消由此带来的双重数值耗散，所以取值有所偏大.而算例1和算例4中尽管也存在间断和极值，但不在同一点出现，因此数值耗散没有那么大，所以θ取值较小.关于混合格式的研究近年来已有不少学者进行了研究，如文献［7－8］等.本文对混合参数的详细研究会在后续的工作中进行.

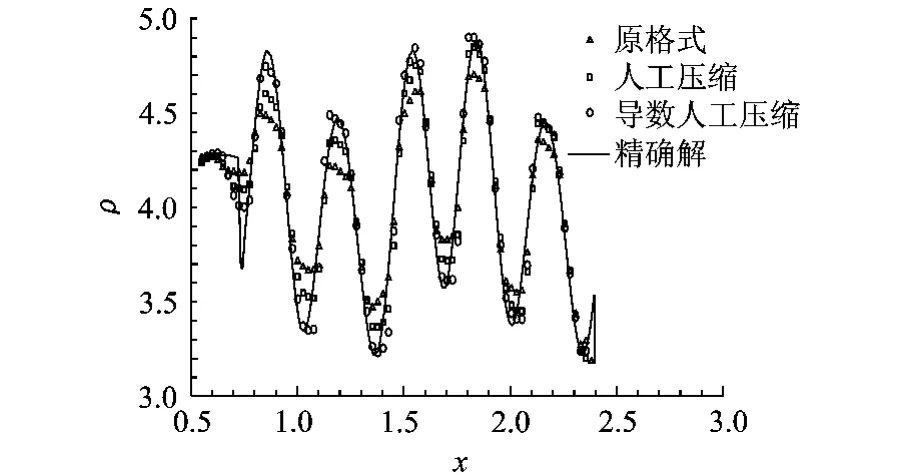
图9 三种格式密度分布局部放大图比较

3 结论

比较上述数值实验，可以看出人工压缩方法比原TVD格式在间断处和极值点处都提高了分辨率，本文发展的导数人工压缩格式又比人工压缩方法在极值点处提高了分辨率.当脉动多而网格不够密时，一般格式可能会完全或部分丧失对脉动的分辨力，本文提出的导数人工压缩法则能在相同情形较准确地分辩脉动，这种特性对于网格数不能太大的三维流体计算很有价值，特别是对脉动比较多的流场 (如湍流)更有价值.

References)

［1］Harten A.The artificial compression method for computation of shocks and contact discontinuities［J］.Communications on Pure and Applied Mathematics，1977，30(5):611－638

［2］Harten A.High resolution schemes for hypersonic conservation laws［J］.Journal of Computational Physics，1983，49(2):357－393

［3］Dong Haitao，Zhang Lidong，Lee Chun-Hian.High order discontinuities decomposition entropy condition schemes for Euler equations［J］.Computational Fluid Dynamics Journal，2002，10(4):448－457

［4］Harten A，Osher S.Uniformly high-order accurate non-oscillatory schemes［J］.SIAM J Numer Anal，1987，24(2):279 －309

［5］Shu C W，Osher S.Efficient implementation of essentially nonoscillatory shock-capturing schemesⅡ ［J］.Journal of Computational Physics，1989，83(1):32 －78

［6］Lie K A，Noelie S.On the artificial compression method for second-order non-oscillatory central difference schemes for systems of conservation laws［J］.SIAM J Sci Comput，2003，24(4):1157－1174

［7］Ren Y X，Liu M E，Zhang H X.A characteristic-wise hybrid compact-WENO scheme for solving hyperbolic conservation laws［J］.Journal of Computational Physics，2003，192(2):365－386

［8］Ziegler J L，Deiterding R，Shepherd J E，et al.An adaptive high-order hybrid scheme for compressive，viscous flows with detailed chemistry ［J］.Journal of Computational Physics，2011，230(20):7598－7630