铁木辛柯梁固有振动频率的边界元解法

金 晶 邢誉峰

(北京航空航天大学 航空科学与工程学院，北京100191)

边界元法作为现代数值方法之一，其基本思想是用边界积分方程求解微分方程，但直至20世纪60年代人们才认识到它的价值［1－3］.边界元方法具有降低问题的维数、计算精度高等优点，其应用领域已遍及弹塑性力学、岩土力学、热学、声学、电磁学、生物细胞学等［4－9］.近年来，随着高性能大容量微机的出现，边界元法广泛应用于大型和非线性科学工程领域的数值计算，已成为一种强有力的数值计算方法.

梁、板作为常用的工程结构元件，探索其自由振动固有频率的求解方法对认识和参数设计结构动态性能具有重要意义.文献［10］用边界方法(BEM，Boundary Element Method)分析了欧拉梁振动问题，包括欧拉梁纵向、扭转、弯曲振动的频率特性，提出了局部区间步长细化频率扫描方法，但对精度和可行性未作深入分析.文献［11－12］用静态基本解分析了薄板的动态特性.静态基本解表达式虽然简单，但精度得不到保证.文献［13］使用动态基本解分析了薄板的动态特性，但板的动态基本解比较复杂，在处理奇异积分时需要花费大量时间，给编程和数值计算带来困难.

为了充分发挥边界元方法本身高精度和高效率的优势，利用杆、梁等一维结构固有振动的基本解来处理二维固有振动问题将是一条有效的途径.截至目前，杆 (轴)和欧拉梁的基本解是已知的［14］，而具有两个广义位移的剪切梁的基本解却未见公开发表.基于这种情况，本文首先推导了铁木辛柯梁的基本解，建立了相应的边界积分方程.为了简洁起见，以杆为例从理论上证明边界元法处理一维问题时得到的频率是精确的，分析了代数特征值求解方法和影响系数方法的特点.最后给出了剪切梁的数值算例.

1 铁木辛柯梁自由振动的边界方程

1.1 基 本 解

基本解是边界元方法的核心.不同问题基本解的求解方法也不同，对于一维问题，可用单位载荷方法或Duhamel积分;二维和三维弹性力学问题的基本解为Kelvin解;对于用Laplace和Poisson等方程描述的位势问题，可应用格林第二公式来求解.此外还有通用的傅里叶变换和特征函数展开方法.下面用傅里叶变换方法推导铁木辛柯梁的基本解.与欧拉梁不同的是，铁木辛柯梁具有两个独立变量，这类似于二维问题.而与二维问题不同的是，铁木辛柯梁的两个独立变量 (挠度和转角)具有不同的量纲，又只是轴向坐标的函数.因此，为了求基本解，先对变量进行无量纲化.

铁木辛柯梁固有振动的特征微分方程［14］为

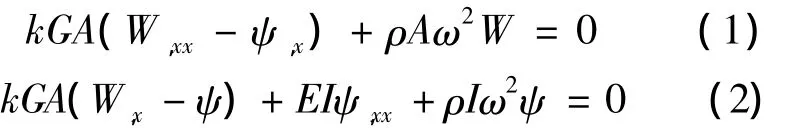
式中，W为挠度函数;ψ为转角函数;EI为弯曲刚度;ρ为密度;kGA 为剪切刚度;()，x和 ()，xx分别表示对坐标x的一阶微分和二阶微分.

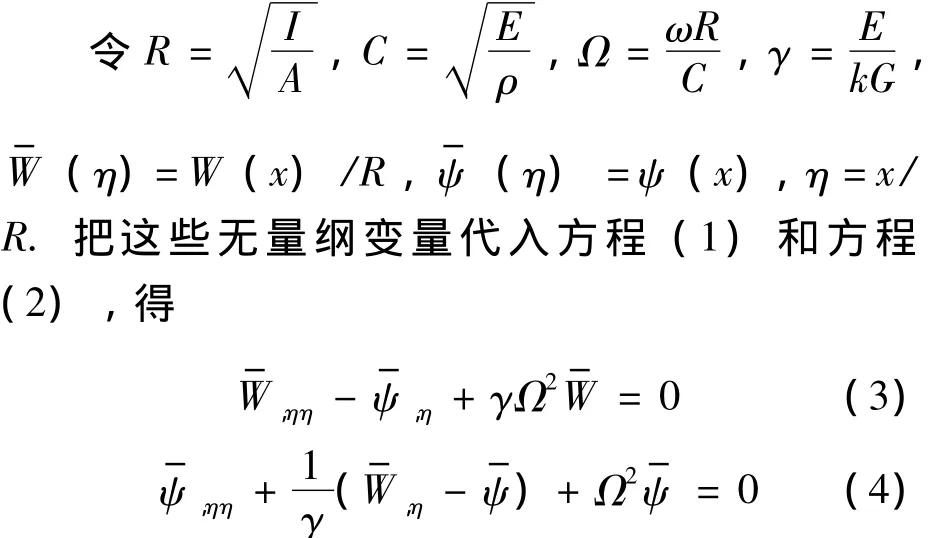
与之对应的铁木辛柯梁基本解方程为

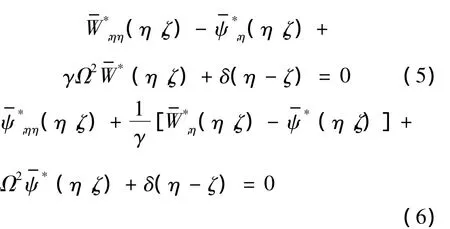
式中，δ(η－ζ)为狄拉克函数，ζ和η分别为测点和源点.

根据傅里叶变换，结合梁无穷远处的边界条件 (挠度、转角、弯矩和剪力为0)可得挠度和转角的基本解分别为

式中的λ1和λ2有下面两种不同的形式:

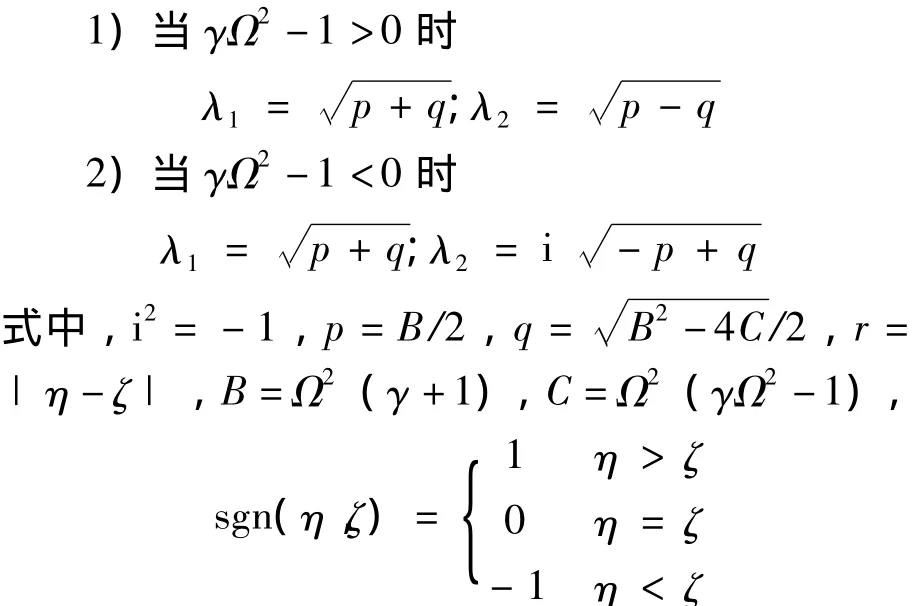
而剪力和弯矩的基本解为

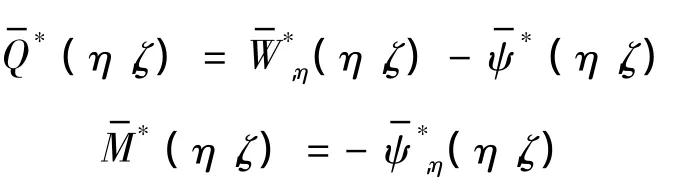
1.2 边界积分方程

建立边界积分方程是实现边界元方法的关键步骤.利用基本解建立边界积分方程的方法有加权残量法、格林公式法和功的互等定理等.这里采用加权残量法来建立铁木辛柯梁的边界积分方程.同样也可以建立杆和欧拉梁的边界积分方程.

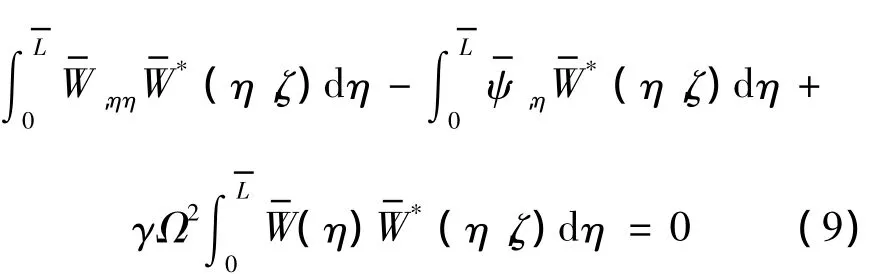
对第1项分部积分两次，第2项分部积分一次得

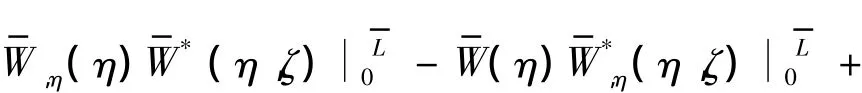
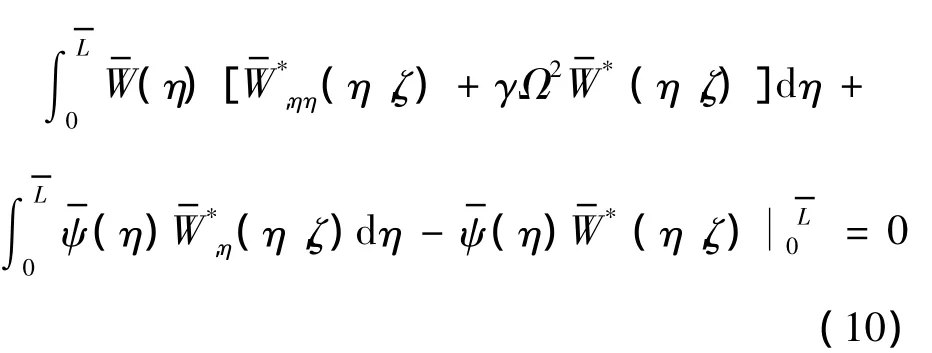
同理，对式 (4)加权得

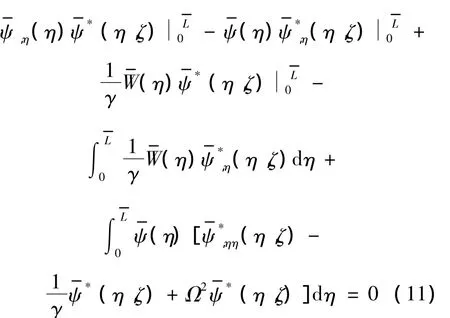
用γ乘以式 (11)，再把所得结果与式 (10)相加，并利用基本解式 (5)和式 (6)得

将式 (12)对ζ求一阶导数得

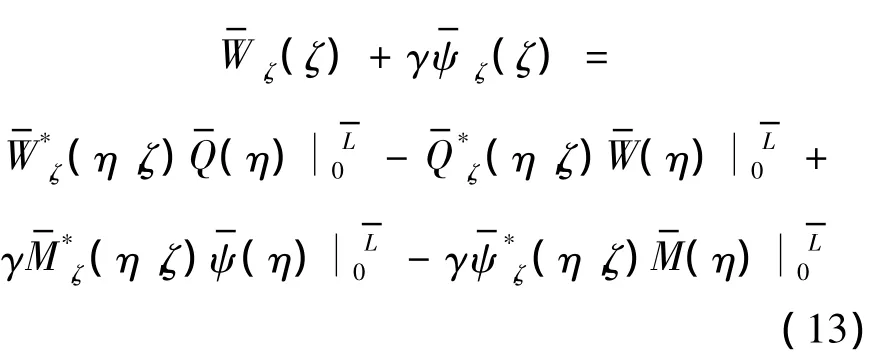
式中系数矩阵分别为

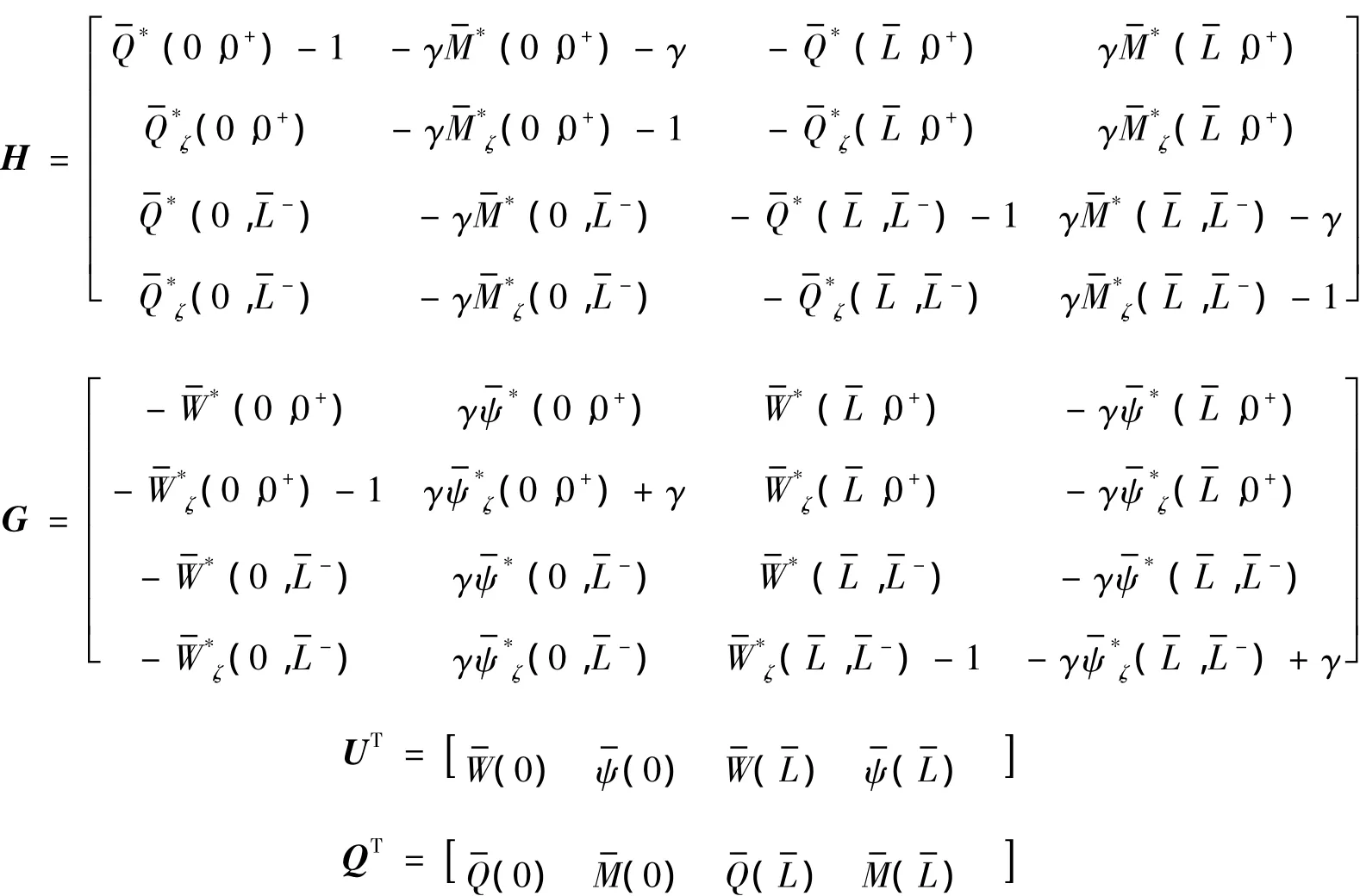
如果梁两端有平动弹簧和转动弹簧约束，只要通过弹簧刚度系数建立剪力和弯矩与挠度和转角关系，则可以正确模拟任意边界条件.下面讨论用代数特征值方程和影响系数法求解频率时各自的特点.

2 固有振动边界方程的解法

一维问题边界包括两个端点，不存在边界离散误差，并且域内采用基本解，因此可以推断用BEM求得的频率一定是精确的.为了简单起见，本节以均匀杆为例，来达到两个目的:①证明用BEM求得的一维结构频率是精确的;②讨论代数特征值方法和影响系数法.本节的证明方法和频率的解法同样适用于梁.

与铁木辛柯梁情况类似，可推导出杆的边界方程式如下:

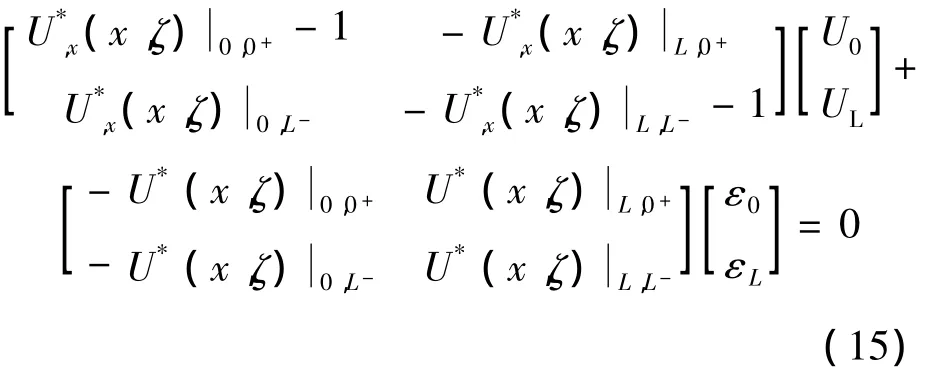
式中，U0和UL分别为杆两端的位移;ε0和εL分别为两端的应变;而基本解U*为

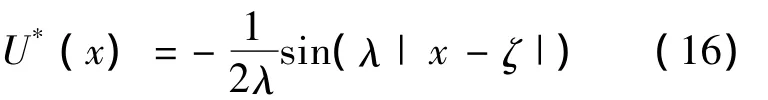
其中λ为频率参数.

1)代数特征值方法

考虑两端固支杆，约束条件为U0=0和UL=0.由式 (15)得频率方程为

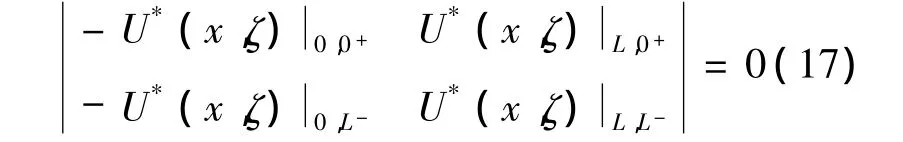
化简为

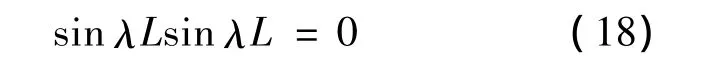
同理可以得到两端自由的频率方程为

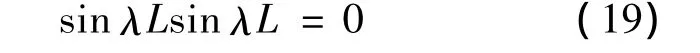
而左端固支右端自由的频率方程为

从方程式 (18)～方程式 (20)可以看出，用代数特征值方法得到的三种不同边界条件下的频率方程中不但包括各自的精确频率方程，也包括自由频率方程.欧拉梁问题类似，即用这种方法得到的固支、自由、简支、悬臂梁以及弹性支持的频率方程中都包含自由梁的频率方程.这应该起因于基本解的性质.值得指出的，对于不同边界条件的铁木辛柯梁，多出来的频率并不是自由情况的频率，这有待于深入研究.

2)影响系数方法

这种方法的核心是根据式 (15)得到用未知量表示已知量的关系式.以左端固支右端自由杆为例，其结果为

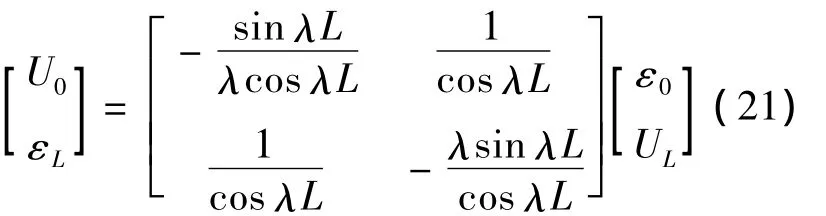
式中系数矩阵的对角元素为影响系数，其变量为频率.当频率为系统固有频率时，影响系数为无穷大，据此可以确定系统的固有频率.从式(21)容易看出，一端固支杆的频率方程为cos λL=0.对于自由杆和固支杆情况，可以用类似的方法进行分析.

在进行数值计算时，需要对频率进行扫描，其步长将决定这种方法的精度和效率.

3 数值分析

由于铁木辛柯梁的基本解比较复杂，直接从方程 (14)推导显式形式的频率方程比较困难.于是，下面根据影响系数法求解其固有振动频率，并与精确解［15］和NASTRAN结果 (用50个BEAM单元)进行比较，见表1.梁长0.05 m，矩形截面高0.01 m，宽0.01 m，弹性模量7×1010N/m2，剪切系数5/6，泊松比0.31，质量密度2700 kg/m3.

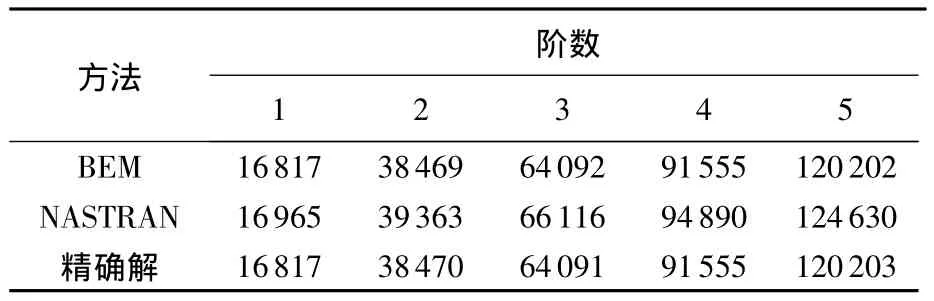
表1 固支梁的频率 Hz

表1中BEM的结果是用扫描步长1 Hz得到的，如此得到的近似频率和精确解之间的绝对误差不超过1.图1给出了频率和影响系数的关系曲线.由于NASTRAN中的BEAM单元不考虑转动惯量的影响，因此对应的每一阶频率都偏大.

当改变均匀梁的截面形状时，只是改变了截面惯性矩.因此，用本文方法可以给出任意截面形式且具有任意边界条件梁的精确频率方程.

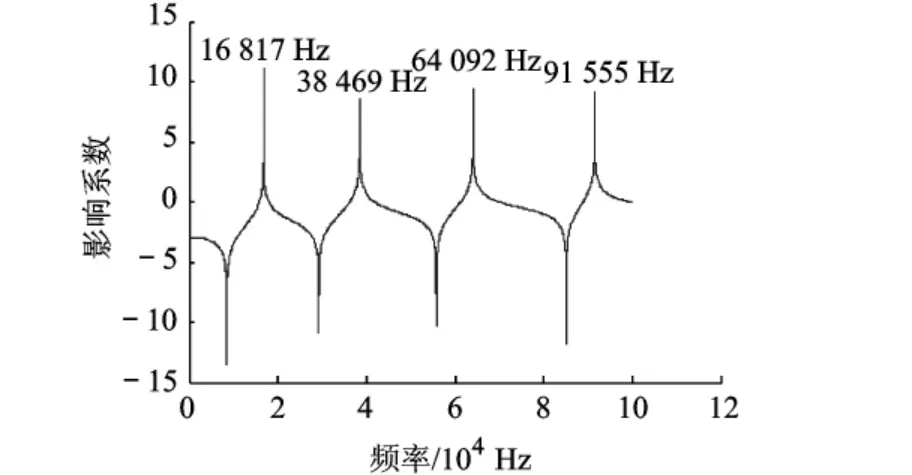
图1 固支梁的频率－影响系数关系曲线

4 结论

基于理论推导和数值分析，可得出如下结论:

1)对于一维均匀结构，没有边界离散误差，用边界元法得到的频率是精确解.

2)采用代数特征值方法求解频率时，由于基本解本身的特性，对于不同结构不同边界条件求出的频率都包含多余的频率.

3)采用影响系数方法求固有频率，避免了多余频率的出现，但其精度和效率取决于频率扫描步长.

4)根据已有的杆、欧拉梁的基本解和本文推导的剪切梁的基本解，可以简化用边界元法分析二维结构固有振动特性的过程.这是下一步要开展的研究工作.

References)

［1］Brebbia C A，Walker S.Boundary element techniques in engineering［M］.London:Newnes-Butterworths，1980

［2］Brebbia C A，Telles J C F，Wrobel L C.Boundary element techniques-theory and applications in engineering［M］.New York:Springer-Verlag，1984

［3］杨德全，赵忠生.边界元理论及应用［M］.北京:北京理工大学出版社，2002

Yang Dequan，Zhao Zhongsheng.The theory and application of boundary element method［M］.Beijing:Beijing Institute of Technology Press，2002(in Chinese)

［4］Wei X，Leu L J，Chandra A.Shape optimization in elasticity and elasto-viscoplasticity by the boundary element method ［J］.International Journal of Solids and Structures，1994，31(4):533－550

［5］Chen Chao-shi，Pan ernian，Amadei Bernard.Fracture mechanics analysis of cracked discs of anisotropic rock using the boundary element method［J］.International Journal of Rock Mechanics and Mining Sciences，1998，35(2):195－218

［6］Bialecki R A.Solving heat radiation problems using the boundary element method［M］.Boston:Computational Mechanics Publications，1993

［7］陈剑，高煜，张永斌，等.基于有限元-边界元的声学构形灵敏度分析［J］.振动工程学报，2009，22(2):213－217

Chen Jian，Gao Yu，Zhang Yongbin，et al.Acoustic configuration sensitivity analysis based on FEM and BEM［J］.Journal of Vibration Engineering，2009，22(2):213－217(in Chinese)

［8］林庆华，栗保明.有限元/边界元耦合法计算电磁轨道炮三维瞬态涡流场 ［J］.南京理工大学学报:自然科学版，2010，34(2):218－221

Lin Qinghua，Li Baoming.Finite-element/boundary-element coupling method for 3D transient eddy current field calculation in electrom agnetic railgun［J］.Journal of Nanjing University of Science and Technology:Natural Science，2010，34(2):218－221(in Chinese)

［9］彭红梅，杨德全.双分叉动脉血流动力学特性的边界元分析 ［J］.医用生物力学，2010，25(4):283－287

Peng Hongmei，Yang Dequan.Boundary element analysis on characteristics of double bifurcation arterial hemo-dynamics［J］.Journal of Medical Biomechanics，2010，25(4):283 －287(in Chinese)

［10］黄玉美，张广鹏，高峰.虚拟样机整机结构特性边界元法仿真［M］.北京:机械工业出版社，2004

Huang Yumei，Zhang Guangpeng，Gao Feng.The simulation with boundary element method of the whole structural characteristics for the virtual prototype［M］.Beijing:China Machine Press，2004(in Chinese)

［11］Jesus A，Costa J.Plate vibrations using BEM［J］.Application Mathematics Modelling，1988，12:78－85

［12］Tanaka M，Matsumoto T，Shiozaki A.Application of boundary-domain element method to the free vibration problem of plate structures［J］.Computers ＆ Structures，1998，66(6):725－735

［13］Providakis C P，Beskos D E.Free and forced vibrations of plates by boundary elements［J］.Computer Methods in Applied Mechanics and Engineering，1989，74(3):231:250

［14］邢誉峰，李敏.计算固体力学原理与方法 ［M］.北京:北京航空航天大学出版社，2011

Xing Yufeng，Li Min.The theory and method of computational solid mechanics［M］.Beijing:Beijing University of Aeronautics and Astronautics Press，2011(in Chinese)

［15］邢誉峰，李敏.工程振动基础 ［M］.北京:北京航空航天大学出版社，2011

Xing Yufeng，Li Min.The foundation of engineering vibration［M］.Beijing:Beijing University of Aeronautics and Astronautics Press，2011(in Chinese)