三维引力辅助机理分析

贾建华 王 琪

(北京航空航天大学 航空科学与工程学院，北京100191)

引力辅助技术 (gravity-assist)，又称借力飞行或引力甩摆，是一种航天任务中经常用来减少燃料消耗的方法.目前已经有多个任务利用引力辅助技术设计了行星际探测轨道，完成了太阳系八大行星的探测任务［1］.

引力辅助技术起源于18世纪，Laplace、leverrier、Tisserand用此来解释行星对彗星轨道的摄动，Lawden首先提出可将引力辅助技术应用于飞行器［2］.目前对引力辅助技术的研究主要集中在应用方面，如引力辅助序列的选取［3－4］、小推力引力辅助的研究［5－6］、气动引力辅助的研究［7－8］，而对引力辅助机理本身的探讨和研究较少.1988年文献［9］对二维引力辅助机理进行了分析，给出了前侧飞越使飞行器能量减少、后侧飞越使飞行器能量增加等重要结论，揭开了人类对引力辅助机理认识的新篇章，但讨论仅限于平面圆型限制性三体问题.1997年文献 ［10］采用平面椭圆型限制性三体模型对引力辅助机理进行了深入研究，结果表明，偏心率和真近点角对引力辅助轨道具有重要影响.文献 ［11－12］也对基于平面限制性三体问题模型的引力辅助机理进行了一些讨论.以上的研究都只限于二维引力辅助，飞行器运动被限制在借力天体的运动平面内，这显然不能满足实际任务的需要.目前，对三维引力辅助机理的研究尚不多见，文献［13］初步讨论了面外角对引力辅助轨道的影响，但是，对面外角的研究较为简略，而且对飞行器近心点速度有一定限制，因此需要对三维引力辅助机理进行进一步的研究.

为此，本文在前人研究工作的基础上，通过引入两个参数，将对引力辅助机理的探讨从平面椭圆型限制性三体模型拓展到三维椭圆型限制性三体模型，重点讨论了这两个参数对引力辅助前后的飞行器轨道类型、轨道能量和轨道倾角的影响.最后，以地月系统为例，针对不同任务要求，给出了引力辅助参数的选择区域，并对引力辅助参数进行了优化.

1 问题描述

在三维椭圆型限制性三体模型下，三维引力辅助可通过6个自由参数来描述 (如图1所示):①Vp:飞越借力天体时近心点处的速度;②rp:飞越借力天体时近心点距离;③ν:借力天体的真近点角;④ψ:rp在x-y平面的投影与M1，M2连线的夹角;⑤α:rp与x-y平面的夹角;⑥β:VP与x-y平面的夹角.

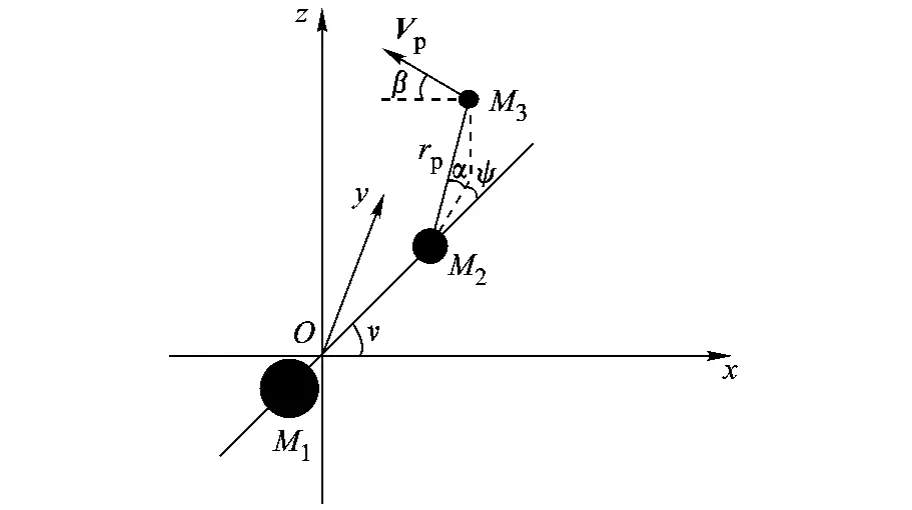
图1 三维椭圆型限制性三体模型引力辅助示意图

2 三维椭圆型限制性三体模型

假设两个主天体分别为M1和M2，绕其公共质心做椭圆运动，第三体M3(本文中为飞行器)的质量远远小于两个主天体的质量，在两个主天体的作用下运动，而不影响两个主天体的运动.M3的运动轨迹不限于两个主天体的运动平面内，可以是三维的.

为了讨论和计算上的方便，采用无量纲形式，定义:以M1和M2相对轨道的半长轴为单位长度1;平均角速度为1;单位质量为m1+m2，其中，m1，m2分别是 M1和 M2的真实质量，这样，M2的质量可以用μ=m2/(m1+m2)表示，M1的质量为 (1－μ);定义单位时间，使得主天体的运动周期为2π;M1-M2系统的引力常数 (万有引力常数G=6.67×10－11m3·kg－1·s－2与系统总质量的乘积)定义为1.

用于分析此模型的参照系有很多，本文采用惯性坐标系.在惯性系中，坐标原点为M1和M2的公共质心;横轴x是初始时刻连接M1和M2的连线;纵轴y过原点垂直于x轴并且在两个主天体的运动平面内;z轴符合右手定则.在此参考系中，M1和M2的位置分别为

其中，r=(1－e2)/(1+ecosν)，为M1和M2间的距离;ν为M2的真近点角;e为椭圆轨道的偏心率.

M3的动力学方程可表示为

其中，r1，r2分别为M3到M1和M2的距离.

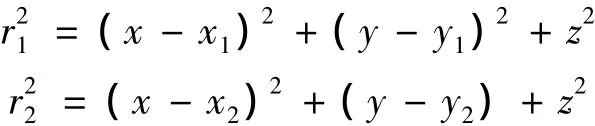
此外，时间和真近点角的关系为

其中，p=a(1－e2)，为椭圆的半正交弦.

可以求解出此惯性系下，M3的能量EI和角动量CI分别为

其中，RI是M3的矢径;VI是M3的速度向量.则M3的轨道倾角i=arccos(CIz/|CI|)，其中，CIz为CI的z轴分量.

3 数值算法

由于椭圆型限制性三体问题目前无法得到轨道变化的解析表达式，所以只能通过数值积分进行分析.数值算法流程如下:

1)给参数Vp，rp，ν，ψ，α，β，e，μ赋初值.

2)计算M3的初始位置和初始速度:

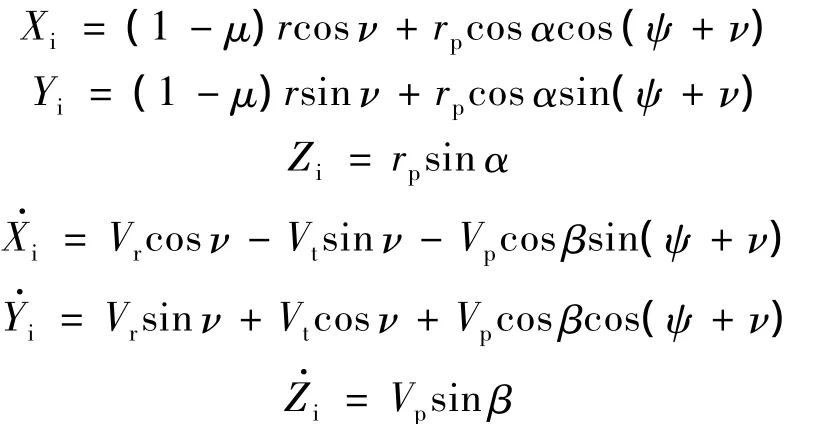
3)在初始条件下，对动力学方程进行向前积分，直到M3与M2的距离大于指定距离d时停止.计算出引力辅助之后飞行器的能量E+和角动量C+.

4)在初始条件下，对动力学方程进行向后积分，直到M3与M2的距离大于指定距离d时停止.计算出引力辅助之前飞行器的能量E－和角动量C－.

本文所有数值模拟，指定距离d都为0.5，通过变化参数的初值，可以研究参数对引力辅助轨道的影响.

4 数值仿真

根据轨道动力学的基本定义:轨道能量为“正”表示双曲线轨道， “负”表示椭圆轨道;角动量z轴分量为“正”表示顺行轨道，“负”表示逆行轨道.根据得到的E－，C－，E+，C+，可以将引力辅助轨道划分为16种类型，分别用前16个英文字母表示，具体见表1.

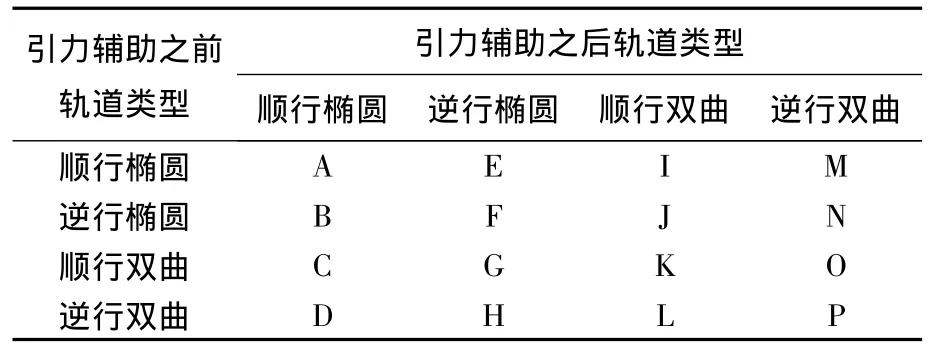
表1 英文字母与轨道类型的对应关系

关于引力辅助参数Vp，rp，ν，ψ对飞行器轨道的影响，文献 ［9－13］已经进行了讨论，在此不再赘述.本文将重点讨论参数α和β对引力辅助前后的飞行器轨道类型、轨道能量和轨道倾角的影响.

4.1 参数α的分析

4.1.1 α对引力辅助前后轨道类型的影响

本文对大量不同的α取值进行了仿真，特选取了其中较有代表性的情况，见图2.图2所示是 α 分别为0°，60°，90°，120°时的 ψ-Vp图，图中字母代表对应的轨道类型.其他参数取值分别为:μ=0.012 1，rp=0.004 95，e=0，ν=0，β=0.此组参数下，0＜ψ＜π图形与π＜ψ＜2π图形关于ψ=π镜像 (镜像规律:B和E，C和I，D和M，G和J，H和N，L和O互为镜像，A，F，K，P不变)，因此只给出ψ为π～2π时情况;α与360°－α的图形完全相同，因此只给出α为0°～180°情况.

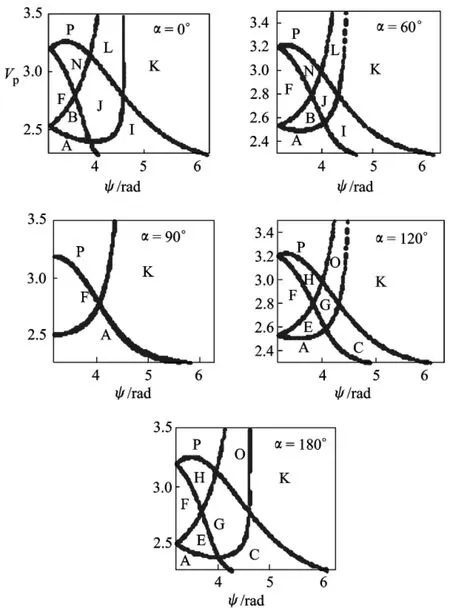
图2 α对引力辅助轨道类型的影响

当α=β=0°时，三维椭圆型限制性三体问题就退化为平面椭圆型限制性三体问题，三维引力辅助退化为二维引力辅助，本文结果与文献［10］的结果完全相同，说明本文对三维引力辅助机理的研究可以很好地退化到二维情况.

当α≠0°时，引力辅助为三维情况.从图2可以看到:随着α的变化，各种轨道类型区域均发生变化.现将其变化规律总结如下:

1)椭圆轨道区域 (引力辅助前后都为椭圆轨道，包含类型A，B，E，F)总是出现在左下方.α从0°～90°，整体区域增大，A，F增大，B减小;α=90°时B消失;α从90°～180°，整体区域减小，A，F减小，E(B的镜像类型)增大.

2)双曲轨道区域 (引力辅助前后都为双曲轨道，包含类型K，L，O，P)总是出现在右上方.α从0°～90°，整体区域增大，K，P增大，L减小;α=90°时L消失;α从90°～180°，整体区域减小，K、P减小，O(L的镜像类型)增大.

3)逃逸轨道区域 (引力辅助前后分别为椭圆轨道和双曲轨道，包含类型I，J，M，N)总是夹在椭圆轨道区域和双曲轨道区域之间.α从0°～90°，整体区域缩小，I，J，N均减小;α=90°时均消失;α为90°～180°时，不出现.

4)俘获轨道区域 (引力辅助前后分别为双曲轨道和椭圆轨道，包含类型C，D，G，H)总是夹在椭圆轨道区域和双曲轨道区域之间.α为0°～90°时，不出现;α从90°～180°，整体区域增大，C，G，H均增大.

5)逆行轨道区域 (引力辅助前后都为逆行轨道，包含类型F，H，N，P)总是出现在左上方.α从0°～90°，整体区域略有增大，F，P增大，N减小;α=90°时N消失;α从90°～180°，整体区域略有减小，F，P减小，H(N的镜像类型)增大.

6)顺行轨道区域 (引力辅助前后都为顺行轨道，包含类型A，C，I，K)总是出现在右半部和底部 ，一直占据大部分.α从0°～90°，整体区域增大，A，K增大，I减小;α=90°时，I消失;α从90°～180°，整体区域减小，A，K减小，C(I的镜像类型)增大.

7)逆行变顺行轨道区域 (引力辅助前后分别为逆行轨道和顺行轨道，包含类型B，D，J，L)总是夹在逆行轨道区域和顺行轨道区域之间.α从0°～90°，整体区域缩小，B，J，L均减小;α=90°时均消失;α为90～180°时，不出现.

8)顺行变逆行轨道区域 (引力辅助前后分别为顺行轨道和逆行轨道，包含类型:E，G，M，O)总是夹在逆行轨道区域和顺行轨道区域之间.α为 0°～90°时，不出现;α从 90°～180°，整体区域增大，E，G，O均增大.

4.1.2 α对飞行器能量的影响

图3所示为α对飞行器能量变化的影响.其中参数设置如下:μ=0.012 1，rp=0.004 95，e=0，ν=0，β=0，ψ =20°，Vp=2.6.

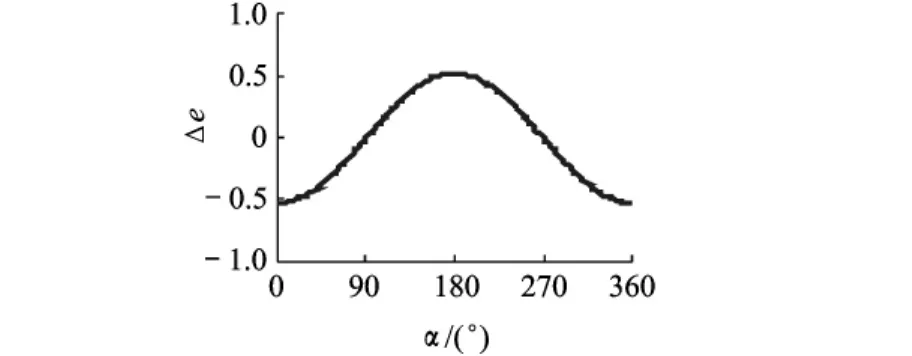
图3 α对轨道能量变化的影响

可以看到，曲线呈钟形，关于 α=180°对称.α=0°或180°时，引力辅助前后飞行器轨道能量改变最大.当α=90°或270°时，Δe=0.本文对其他rp值进行了模拟，所得曲线仍呈钟形.

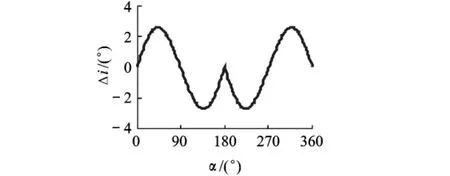
图4 α对轨道倾角变化的影响

4.1.3 α对飞行器轨道倾角的影响

图4所示为α对飞行器轨道倾角变化的影响.参数设置与图3相同.

可以看到，图形关于α=180°对称.α=0°～180°曲线形状类似于正弦曲线.α =0°，90°，180°，270°时，Δi=0.本文对其他 rp值进行了模拟，所得曲线形状类似.

4.2 参数β的分析

4.2.1 β对引力辅助前后轨道类型的影响

本文对大量的不同β取值进行了仿真，特选取了其中较有代表性的情况，见图5.图5所示是β分别为 0°，67.5°，75°，90°，105°，112.5°，180°时的ψ-Vp图，其他参数取值分别为:μ=0.0121，rp=0.00495，e=0，ν=0，α=0.此组参数下，0＜ψ＜π图形与π＜ψ＜2π图形关于ψ=π镜像 (镜像规则与4.1.1节中相同)，因此只给出ψ为π～2π时情况;β与360°－β的图形完全相同，因此只给出β为0°～180°情况.

从图5可以看到:随着β的变化，各种轨道类型区域均发生变化.现将其变化规律总结如下:

1)椭圆轨道区域总是出现在左下方、右下方.β从0°～180°，左下方区域减小，右下方区域增大;B，F初始在左下角，不断减小至消失，后又从右下角出现，并不断增大.

2)双曲轨道区域总是出现在上部.β从0°～90°，整体区域增大，P，L先增大后减小;β=75°时 P，L消失，只剩 K;β从 90°～180°，整体区域减小;P，L又从右上角出现.

3)逃逸轨道区域总是出现在椭圆轨道区域和双曲轨道区域之间.β从0°～67.5°，J，N均减小;β=67.5°时J，N消失，只剩下I;β从112.5°～180°，J，N再次出现并不断增大.

4)俘获轨道区域没有出现在图中，在ψ为0°～180°中会出现.

5)逆行轨道区域，β为0°～67.5时，出现在左上方;β为0°～67.5°时，出现在右上方.β从0°～67.5°，整体区域减小;β=67.5°时消失;β从112.5～180°，F，N，P都再次出现并不断增大.

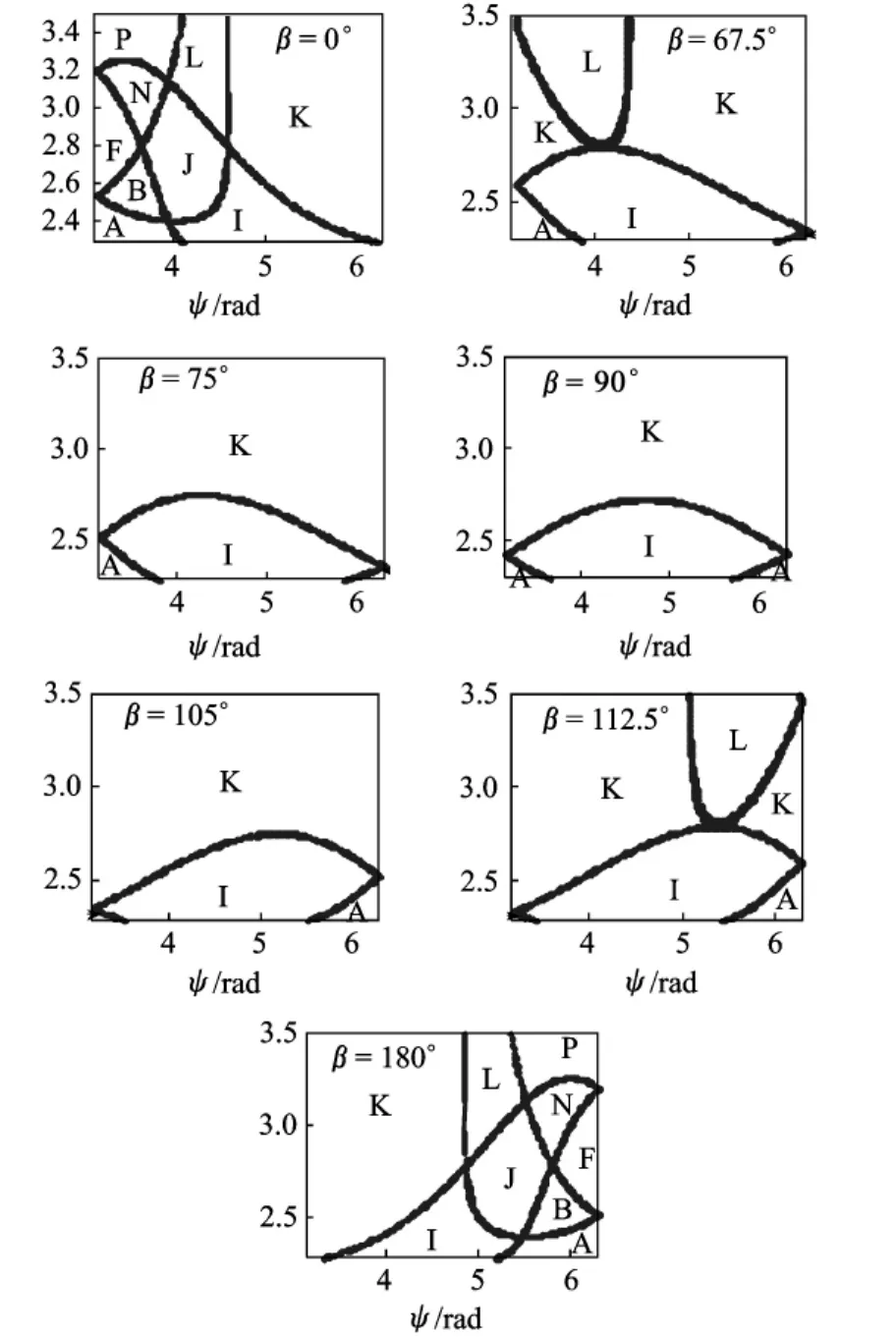
图5 β对引力辅助轨道类型的影响

6)顺行轨道区域一直占据大部分.β从0°～75°，整体区域增大，从右侧不断向左侧扩张(主要是K在扩张);β为75°～105°时独占整个平面;β从105°～180°，整体区域减小，向左侧缩小 (主要是K在缩小).

7)逆行变顺行轨道区域总是出现在逆行轨道区域和顺行轨道区域之间.β从0°～75°，向上部移动，β=75°时均消失;β为75°～105°时，不出现;β为105°～180°时，B，J，L 再次出现.

8)顺行变逆行轨道区域没有出现在图中，在ψ为0°～180°中会出现.

4.2.2 β对飞行器能量的影响

图6所示为β对飞行器能量变化的影响.参数设置如下:μ=0.0121，rp=0.004 95，e=0，ν=0，α =0，ψ =20°，Vp=2.6.

可以看到，曲线呈钟形，关于β=180°对称;曲线变化幅度很小，说明不同的β引起的轨道能量差别很小.本文对其他rp值进行了模拟，所得曲线仍呈钟形.

4.2.3 β对飞行器轨道倾角的影响

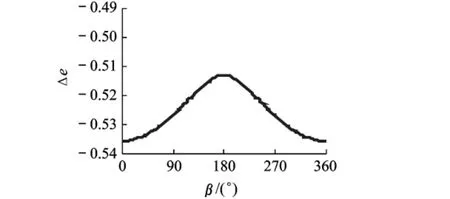
图6 β对轨道能量变化的影响

图7和图8所示为不同rp下β对飞行器轨道倾角变化的影响.其余参数设置与图6相同.

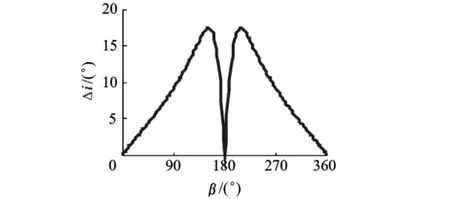
图7 rp=0.008时β对轨道倾角变化的影响

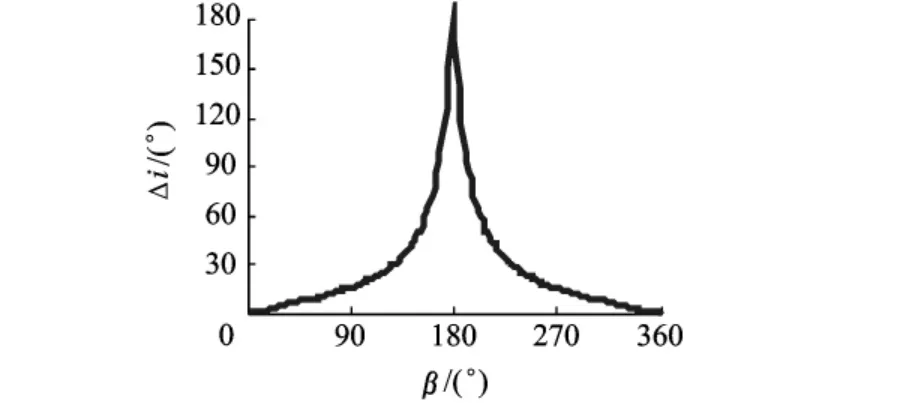
图8 rp=0.00495时β对轨道倾角变化的影响

从图7可以看出:曲线关于β=180°对称.轨道倾角变化的两个峰值约在β=150°和β=210°处取得，而当β=0°或180°时，轨道倾角变化为0.从图8可以看出:此参数下，轨道倾角变化较大，β=180°时，轨道倾角变化为180°，说明轨道发生顺逆转换.本文对其他rp值进行了模拟，发现β=180°时，使轨道发生顺逆转换的临界rp值约为0.00536.

综合图7和图8，可以看到:①图形总是关于β=180°对称;②β=180°时，可能的Δi只有两个值:0°或 180°.

5 以地月系统为例进行参数优化

上述研究对航天器轨道设计具有重要指导意义.在特定任务中，往往需要获得特定轨道类型，如俘获与逃逸、顺行与逆行等，而且往往有一定参数限制，特别对Vp，rp会有一定限制.如果任务目标是对M2进行数据采集，则往往需要设计使Vp和rp最小;如果需要躲避M2的大气层、射线等，则需要使Vp和rp最大.

本文以地月系统为例进行说明.地月系统中，e=0.005 49，μ=0.012 15.限制 rp=0.00504(距月球表200 km)，ν=90°，α =60°，β=30°，限制 ψ 范围为 180°～360°，分别求逃逸、俘获的最大Vp.

从图9可以看出:想要获得逃逸轨道 (I，J，M，N)，最大 Vp为2.75，轨道类型为 I.想要获得俘获轨道 (C，D，G，H)，最大Vp为3.17，轨道类型为H.

图9 ψ-Vp图

6 结论

为了研究三维引力辅助技术，本文通过引入参数α和β，将平面椭圆型限制性三体模型拓展到三维椭圆型限制性三体模型.深入讨论了α和β对飞行器轨道类型、轨道能量和轨道倾角的影响.研究结果表明:

1)α从0°～90°，椭圆轨道、双曲轨道、逆行轨道、顺行轨道整体区域都增大，逃逸轨道、俘获轨道、逆行变顺行轨道、顺行变逆行轨道整体区域都减小;α从90～180°，变化趋势相反.

2)α=90°时，只存在A，F，K，P四种轨道类型，意味着引力辅助前后轨道类型保持不变.α=90°或270°时，引力辅助前后飞行器轨道能量、轨道倾角均保持不变.α=0°或180°时，引力辅助前后飞行器轨道能量改变最大.

3)限定π ＜ψ ＜2π，则只有当0°＜α＜90°时，才存在逃逸轨道和逆行变顺行轨道;只有当90°＜α＜180°时，才存在俘获轨道和顺行变逆行轨道.0＜ψ＜π时的规律，可根据镜像规则得到.

4)β从0°～75°，逆行轨道、逆行变顺行轨道、顺行变逆行轨道整体区域都减小，顺行轨道整体区域增大;β从150°～180°，变化趋势相反.

5)β为75°～105°时，只存在顺行轨道，说明引力辅助前后的轨道只可能是顺行轨道.

6)不论β取何值，只有当π＜ψ＜2π时，才存在逃逸轨道和逆行变顺行轨道;只有当0＜ψ＜π时，才存在俘获轨道和顺行变逆行轨道.

以上的研究和分析揭示了参数α和β对飞行器轨道特性的影响.通过选取适当的参数α和β，可以获得特定任务所需要的轨道类型、轨道能量和轨道倾角.这些研究可以为引力辅助轨道的设计提供依据.

References)

［1］Curtis H D.轨道力学 ［M］.周建华，等译.北京:科学出版社，2009:308－309

Curtis H D.Orbital mechanics for engineering students［M］.Translated by Zhou Jianhua，et al.Beijing:Science Press，2009:308－309(in Chinese)

［2］Flandro G A.From instrumented comets to grand tours:on the history of gravity assist［R］.AIAA 2011-0176，2001

［3］Strange N J，Longuski J M.A graphical method for gravity-assist trajectory design ［J］.Journal of Spacecraft and Rockets，2002，39(1):9－16

［4］Chen K J，Kloster K W，Longuski J M.A graphical method for preliminary design of low-thrust gravity-assist Trajectories［R］.AIAA 2008-6952，2008

［5］Carnelli I，Dachwald B，Vasile M.Evolutionary neurocontrol:a novel method for low-thrust gravity-assist trajectory optimization［J］.Journal of Guidance，Control and Dynamics，2009，32(2):615－624

［6］Pascale P，De Vasile M.Preliminary design of low-thrust multiple gravity-assist trajectories［J］.Journal of Spacecraft and Rockets，2006，43(5):1065－1076

［7］Sims J A，Longuski J M，Patel M R.Aerogravity-assist trajectories to the outer planets and the effect of drag［J］.Journal of Spacecraft and Rockets，2000，37(1):49 －55

［8］Armellin R，le Lavagna M，Ercoli-Finzi A.Aero-gravity assist maneuvers:coupled trajectory and vehicle shape optimization［J］.Celestial Mechanics and Dynamical Astronomy，2006，95:391－405

［9］Broucke R A.The celestial mechanics of gravity assist［C］//AIAA/AAS Astrodynamics Conference.Washington D C:American Institute of Aeronautics and Astronautics，1988:69－78

［10］Prado A F B A.Close-approach trajectories in the elliptic restricted problem ［J］.Journal of Guidance，Control and Dynamics，1997，20(4):797 － 802

［11］乔栋，崔平远，崔祜涛.基于圆型限制性三体模型的借力飞行机理研究［J］.宇航学报，2009，30(1):82－87

Qiao Dong，Cui Pingyuan，Cui Hutao.Research on gravity-assist mechanism in circular restricted three-body model［J］.Journal of Astronautics，2009，30(1):82－87(in Chinese)

［12］乔栋，崔平远，尚海滨.基于椭圆型限制性三体模型的借力飞行机理研究［J］.宇航学报，2010，31(1):36－43

Qiao Dong，Cui Pingyuan，Shang Haibin.Research on gravity-assist mechanism in elliptic restricted three-body model［J］.Journal of Astronautics，2010，31(1):36－43(in Chinese)

［13］Felipe G，Prado A F B A.Classification of out-of-plane swing-by trajectories［J］.Journal of Guidance，Control and Dynamics，1999，22(5):643 －649