翼身组合体的变可信度优化设计

周 婷 吴宗成 陈泽民 朱自强

(北京航空航天大学 航空科学与工程学院，北京100191)

目前，随着计算机性能的飞速发展以及CFD(Computational Fluid Dynamics)理论的不断完善，气动优化设计在许多领域都得到了广泛的应用.优化设计中，目标函数和约束函数的形式往往很复杂，要想利用可信度比较高的方法对其进行分析，可能会使设计时间延长.因此，优化问题常常需要在结果精度和计算时间上做出权衡［1］.

变可信度优化设计的启发式算法已被应用于工程设计问题之中［2］，其优化结果能否保证收敛到高可信度模型优化的最优点是该算法的关键技术，变可信度模型管理有两种方法:①由Dennis等提出的基于一种“模式寻找”方法，这种方法不需要进行梯度计算;②由Alexandrov等提出的近似管理框架 (AMF，Approximation Management Framework)方法，基于一种信赖域思想［3］.这两种方法都可以保证优化结果收敛到高可信度模型优化的最优点.

AMF方法的主要思想是结合高、低可信度模型的优势，优化计算主要在低可信度模型上进行，利用低可信度模型分析得到的结果通常需要重新进行缩放以保证该优化方法得到的结果收敛到高可信度问题的最优点;高可信度模型仅仅起到了修正优化模型的作用，这一方法得益于低可信度模型计算成本低，能够给出好的搜索方向.

在不同网格密度上的同一分析计算模型或是不同分析模型都可以构成变可信度模型.文献［4］采用同一模型对变网格密度时构成的变可信度模型进行了优化设计，同时还进行了不同分析模型组成的变可信度模型的优化设计;文献［5］利用变可信度方法对翼型进行了优化设计，并作了变可信度方法的鲁棒性分析;文献 ［6］利用变可信度方法对多段翼型进行了气动设计.

1 研究方法

1.1 信赖域方法

信赖域方法的提出是基于对非线性函数进行拟合的概念.对任意非线性函数，在某一确定点的邻域内，可以利用局部线化的概念，用一线性函数对其进行近似描述.将“信赖域”的概念应用到优化问题中的信赖域方法，基本思想是首先在设计点上构建优化问题高可信度分析的近似模型，然后根据近似模型与高可信度模型的近似程度确定一个有限的区域，使得利用近似模型对设计变量在给定区域进行优化搜索时，可以得到与高可信度模型相近似的解，该有限区域即为“信赖域”.

对于无约束优化问题

其中，X=(x1，x2，…，xn)T为设计变量，n为设计变量的个数.对于一般的优化问题，都可以构造信赖域法.

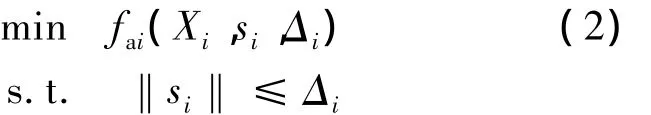
其中，fai是第i次优化分析时用到的近似模型;si为搜索步长;‖‖是Rn中的某一范数;Δi为信赖域半径.信赖域方法的基本过程如下:

1)初始化，给定初始值X0∈Rn，Δ0＞0，i=0.

2)子问题求解，求解信赖域子问题式 (2)得到步长si.

3)如果由步骤2)计算得到的步长si使得f(Xk+sk) ＜ f(Xk)，则接受 si，Xi+1=Xi+si，否则 Xi+1=Xi.

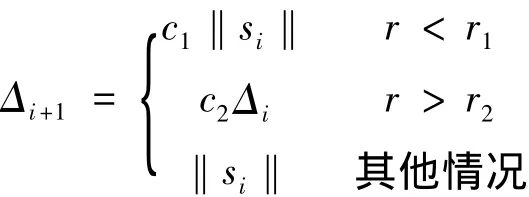
其中，0＜r1＜r2＜1，0＜c1＜c2.通常取 r1=0.2，r2=0.75，c1=0.5，c2=2.

1.2 AMF方法

信赖域方法为如何利用近似计算模型代替高可信度模型提供了基础，如何将这一概念应用到优化过程中，以提高优化质量、降低优化成本的关键在于对高低可信度模型进行管理.Alexandrov等人首先在优化设计中提出了一种基于信赖域方法的AMF方法，这种方法可以对不同可信度的模型进行有效的管理和组织.

传统的优化过程中，分析软件把优化目标及其导数信息f，Δf传递给优化分析器，优化分析器根据接受到的信息搜索到新的设计变量X，传递给分析软件再次进行分析，如此反复直至收敛.如果对该优化问题的目标函数、约束及其导数的分析采用的是高可信度模型，优化所需的计算成本将是巨大的.在AMF方法中，对高可信度模型利用低可信度模型建立一个近似，用fa来表示.在优化搜索中，通过低可信度模型分析，优化器获得近似模型给出的优化目标及其导数，优化器据此搜索到新的设计变量，传递给分析软件进行再次分析，如此反复直至收敛，高可信度模型只是起到修正目标函数近似模型的作用.

AMF方法在构建不同可信度模型结构时会遇到如下问题:①如何给出近似模型相对高可信度模型近似程度的定量表达式;②如何根据该表达式的值来指导下一步优化，即如何调整信赖域的范围，确定下一步优化的起始点Xi+1.

设低可信度模型对物理问题描述准确性的量度值定为r，当r→1时表示低可信度模型与高可信度模型当前的近似程度较好，信赖域可以相应地扩大或者不变，优化结果可以作为下一轮优化的起点Xi+1=Xi+si;当r≪1甚至r＜0时，表示低可信度模型当前近似程度较差，信赖域需要相应地缩小，而且优化结果Xi+si不能被接受，优化起点为原起点Xi.

1.3 零阶近似

根据构造近似模型的原则不同，AMF主要有两种形式，一阶近似和零阶近似.本文采用零阶近似，低可信度模型对高可信度模型零阶近似的构造原则，要求在当前点Xi上，有fa(Xi)=fhi(Xi)成立，其中，fhi和fa分别代表采用高可信度模型和近似模型计算得到的目标函数值.

2 数值方法

本文将多重网格N-S(Navier-Stokes)方程方法作为高可信度模型，它可以较准确地描述流场，对流场参数变化相对比较敏感;低可信度模型采用全位势边界层迭代方法，该方法描述流场的准确度低于N-S方程方法，对于流场参数变化不是很敏感.

2.1 高可信度模型

高可信度模型采用的是多重网格N-S方程方法.采用有限体积法求解翼身组合体绕流的流场，湍流模型为Baldwin-Lomax，控制方程的空间离散采用有限体积方法，无粘通量项和有粘通量项均采用中心差分格式，为了抑制激波及驻点附近的振荡和不稳定性，需要加上人工粘性项.时间推进采用显式五步Runge-Kutta法，采用多重网格技术加速流场解的收敛.

2.2 低可信度模型

低可信度模型采用的是全位势有粘无粘迭代方法［7］，将流动分为两个区域，外部无粘流动区和内部粘性边界层，内层主控方程为边界层方程，外部区域的求解采用绕物体的无粘理论，并考虑物体表面的边界条件和尾迹影响的修正.

边界层外部流场利用全位势方法求解，为消除激波附近解的振荡，引入了人工粘性.采用多重网格方法、残值光顺等技术加速收敛速度.边界层求解利用的是半反方法，整个流场求解时采用准同步有粘无粘迭代.

3 优化设计

根据设计需求不同，机翼的优化设计考虑了两种外型设计参数策略:①保证机翼平面形状不变，通过改变控制剖面的厚度和扭转角来改变机翼的外形;②保持机翼各个剖面的翼型不变，改变机翼的平面形状，对于一般的梯形翼，展弦比、根梢比、前缘后掠角，再加上展长 (半展长)或根弦长，4个量可以唯一地确定一个机翼的平面形状.文献［8］进行过这方面的机翼优化设计研究.采用Powell优化方法进行优化设计.

优化外形选择的是LOCKHEED Wing A梯形翼，其展弦比为7.9，梢根比为0.3998，1/4弦线后掠角为25.0°，半展长为45.7 cm.另外，机翼沿着展向任意横截面最大相对厚度均为0.12，机翼的扭角为 6.5°，安装角为2.5°.机身半径与半展长之比为0.122.

3.1 机翼的厚度扭角优化设计

优化设计的基础外形是LOCKHEED Wing A机翼，沿着机翼的展向选择5个控制剖面，z/b(其中z为展向位置，b为半展长)分别为0.1，0.3，0.5，0.85，1.0.每个控制剖面可以独立地改变厚度和扭转角，此为设计变量，共10个.

优化条件是 Ma=0.818 4，迎角 α=2.940°，Re=0.598×107.目标函数为升阻比CL/CD，优化过程中保持升力系数不变.

选择多重网格N-S方程作为高可信度模型，网格数1378 661，全位势边界层有粘/无粘迭代作为低可信度模型，网格数177174.

调用一次低可信度模型进行流场分析大概需要30 s，调用一次高可信度模型进行流场分析大概需要2 h.高可信度优化调用120次得到优化结果，而变可信度优化只调用N-S方程4次就得到了最终优化结果，大大提高了优化效率.

图1给出了利用3种优化方法得到的翼型最大厚度分布曲线，图2给出了利用3种优化方法得到的扭转角分布曲线，图3给出了利用变可信度优化方法得到的典型截面压强系数曲线的变化情况.表1分别列出了完全利用低可信度模型进行优化、完全利用高可信度模型进行优化以及变可信度优化的优化结果，利用低可信度模型进行优化，目标增益可以达到7.45%，优化结果经N-S方程校核，收益为6.0%，而高可信度优化和变可信度优化结果分别为7.47%，7.26%，可见，低可信度优化结果明显低于另外两个优化结果，而高可信度优化结果和变可信度优化结果几乎类似，但后者计算时间大大减少.

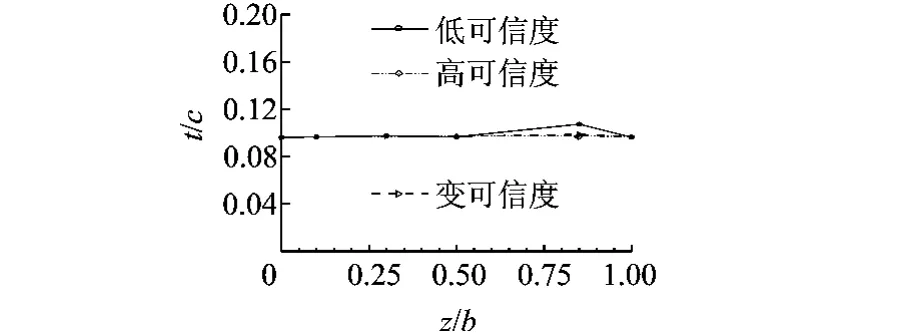
图1 3种优化方法得到的沿展向翼型厚度分布

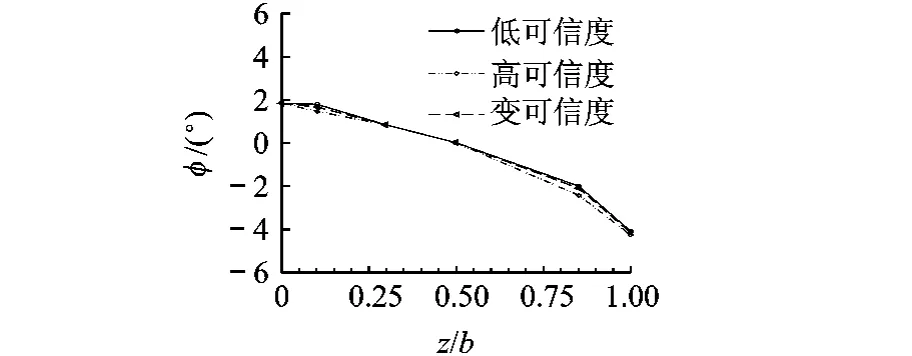
图2 3种优化方法得到的沿展向翼型扭转角分布

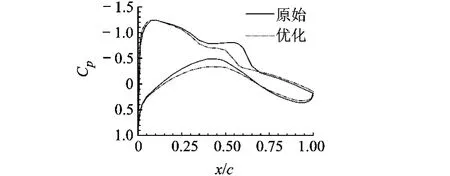
图3 优化前后50%展向位置压强系数Cp弦向分布曲线

表1 Wing A机翼的剖面优化结果对比

3.2 机翼平面形状的优化设计

对于改变机翼平面形状的设计策略也作了研究，保持半展长不变，选择展弦比、根梢比和前缘后掠角为设计变量，改变机翼平面形状.优化设计的基础外形仍是LOCKHEED Wing A.优化条件是Ma=0.818 4，迎角 α=2.940°，Re=0.598×107.目标函数为升阻比CL/CD，优化过程中保持升力系数不变.高可信度优化调用40次得到优化结果，而变可信度优化只调用N-S方程5次就得到了最终优化结果，大大提高了优化效率.

表2分别列出了完全利用低可信度模型进行优化、完全利用高可信度模型进行优化以及变可信度优化的优化结果.可以看到，3种优化设计结果几乎相同，而消耗时间差异很大，本算例低可信度优化也可以获得比较理想的结果.

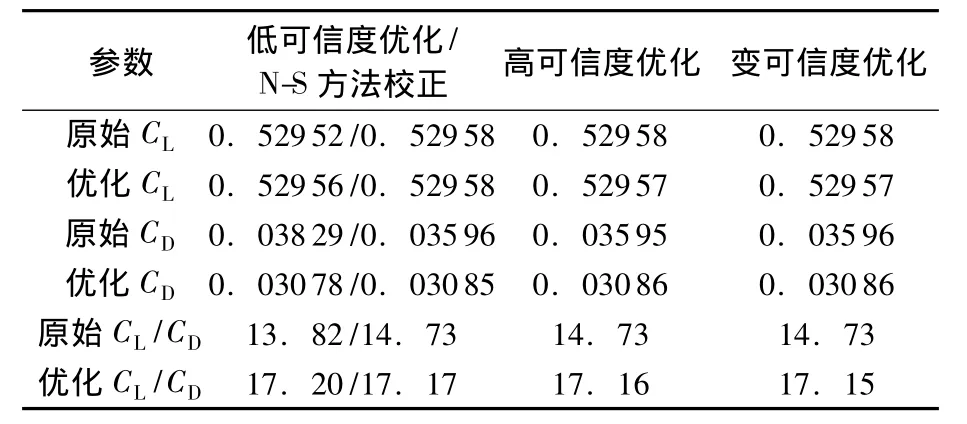
表2 Wing A的平面形状优化结果对比

图4给出了利用变可信度优化，优化前后典型截面的压强分布.图5给出优化前后机翼的平面形状，优化后机翼的展弦比变小，根梢比基本保持不变，前缘后掠角变大.

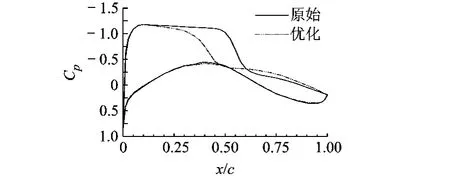
图4 优化前后50%展向位置压强系数Cp弦向分布曲线

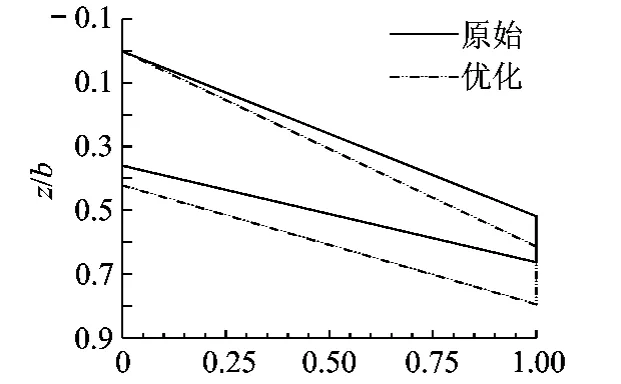
图5 优化前后机翼平面形状

4 结论

优化设计需要对目标函数进行分析计算，如果分析方法比较费时，就会降低优化效率;采用气动力系数的高可信度模型优化，其结果准确性高，但优化效率较低;低可信度模型优化效率高，但优化结果往往需要校核，可能达不到最优解.

本文基于AMF方法发展了翼身组合体变可信度优化方法，进行了机翼厚度扭角优化设计和机翼平面形状优化设计，结果表明，发展的变可信度优化方法可以将优化效率大大提高，同时保证优化效果.

References)

［1］朱自强，王晓璐，吴宗成，等.民机设计中的多学科优化和数值模拟［J］.航空学报，2007，28(1):1－13

Zhu Ziqiang，Wang Xiaolu，Wu Zongcheng，et al.Multi-disciplinary optimization and numerical simulation in civil aircraft design［J］.Acta Aeronautica et Astronautica Sinica ，2007，28(1):1－13(in Chinese)

［2］Egorov I N，Kretinin G V，Leschenko I A，et al.IOSO optimization toolkit-novel software to create better design［R］.AIAA-2002-5514，2002

［3］Alexandrov N M.Robustness properties of a trust region for managing approximations in engineering optimization［R］.AIAA-1996-4102，1996

［4］Alexandrov N M，Lewis R M，Gumbert C R，et al.Approximation and model management in aerodynamic optimization with variable-fidelity models ［J］.J Aircraft，2001;38(6):1093－1101

［5］Marduel X，Tribes C，Trépanie J Y.Variable-fidelity optimization:efficiency and robustness［J］.Optim Eng，2006，7(4):479－500

［6］Wang Jiangfeng，Wu Yizhao，Periaux J.Parallel hierarchical evolutionary algorithms for multi-criteria design optimization problems in aerospace engineering［R］.AIAA-2003-1697，2003

［7］van der Wees A J，van Muijden J，van der Vooren J.A fast and robust viscous-inviscid interaction solver for transonic flow about wing-body configurations on the basis of full potential theory［R］.AIAA-93-3026，1993

［8］王晓鹏，高正红.跨音速翼型和机翼的气动优化设计［J］.应用力学学报，2001，18(2):90－94

Wang Xiaopeng， Gao Zhenghong.Aerodynamic optimization design of transonic airfoil and wing［J］.Chinese Journal of Applied Mechanics，2001，18(2):90－94(in Chinese)