一种基于加速度特征提取的手势识别方法*

陈 意，杨 平，陈旭光

(电子科技大学机械电子工程学院，成都611731)

在现代社会中，手机等移动电子设备已成为人们日常生活中必不可少的通讯和娱乐工具，其主要的交互方式是键盘和触摸屏，而这两种交互方式都不可避免地将用户限制在了设备屏幕之上，降低了操作效率和用户体验［1］。手势拥有自然、直接、易于学习等优点，将其作为移动电子设备现有交互方式的一个补充，将一些简单、频繁的操作采用手势输入，可增强操作的便捷性和趣味性，提升用户体验。

目前，基于加速度传感器的手势识别方法主要有动态时间规整(DTW)［1－4］和隐马尔科夫模型(HMM)［5－8］。然而由于个体差异，同一手势的加速度数据(如幅值、手势长度等)存在较大差异;即使同一个体，同一手势的加速度数据也存在差异。因此上述方法难以建立准确的手势模板和隐马尔卡夫模型，识别准确率较低，个体适应性较差;由于DTW算法的计算量大，随着手势数量的增加，算法实时性将大大降低;并且由于加速度传感器无法获取设备姿态信息，用户只能严格地在给定的设备姿态下操作，这给用户造成了极大的不便。鉴于此，本文提出通过提取反映各类手势运动学特征的加速度特征量及变化规律对手势进行识别，以提高对个体差异的适应性，增强算法鲁棒性和实时性;对于甩动和晃动手势，通过加速度计与陀螺仪相结合获得设备姿态信息，将设备坐标系下的加速度转换到用户坐标系再对其进行识别，简化了这两类手势的识别，同时提高了识别准确率。此外，由于敲击和翻转类手势的识别本身不需要姿态信息，因此本文的十个手势完全取消了设备姿态的限制，用户可以在任意设备姿态下操作手势。

1 手势定义

手势定义应遵循两个原则:①手势易被设备可靠识别;②手势易被使用者学习和记忆［9］。基于上述原则，本文定义了10个手势并按语义及操作的相似性分为4类如表1所示。

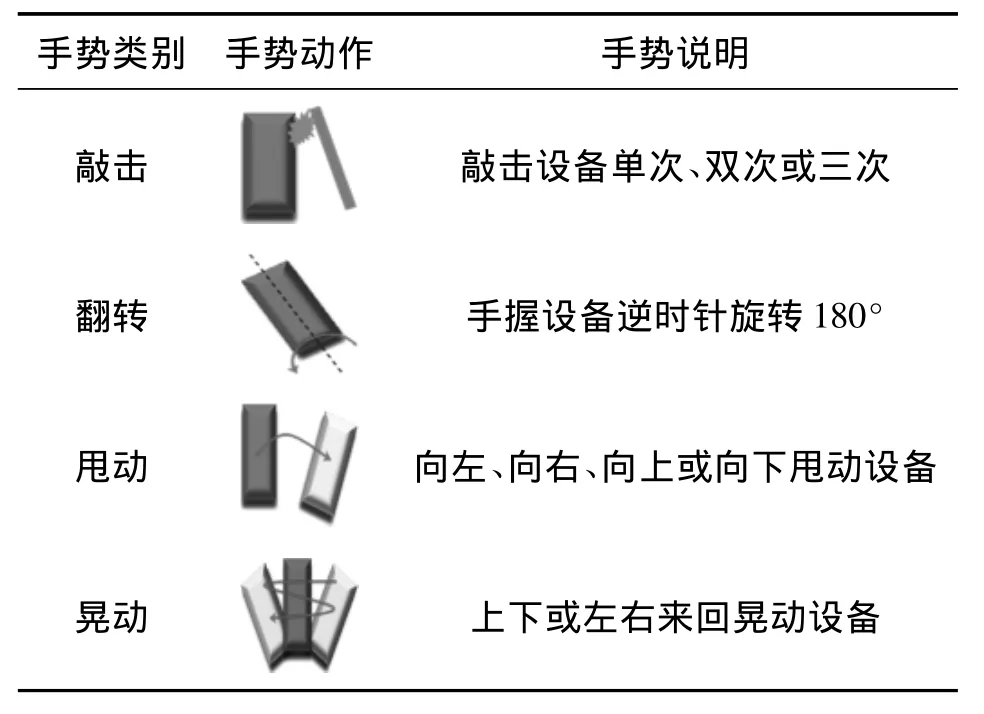
表1 手势定义

2 手势识别算法

手势识别算法如图1所示。

图1 手势识别算法

2.1 手势加速度截取

手势识别第一步是通过准确检测手势起点和终点从而截取手势的加速度数据［10］。如图2所示，本文采用基于加速度变化量的手势检测方法，因为在没有手势产生时，加速度是相对平稳的;而当有手势发生时，加速度变化剧烈。对加速度进行差分可以凸显加速度的变化量，因此本文采用 Δak=|axk－axk－1|+|aykayk－1|+|azk－azk－1|对手势起点和终点进行检测:

其中，N为采样数据个数，Mth为起点和终点检测阈值。N的引入是为了消除由环境噪声及用户抖动等偶然因素引起的误检测。

图2 手势起点与终点检测

2.2 加速度特征量提取

特征提取直接关系到手势识别准确率，因此提取的特征量必须反映各类手势的运动学特性，并且与其他类手势存在明显差异。通过对样本数据(15位实验者，每位实验者操作每个手势各100次)进行分析后，本文定义了手势长度、手势能量［12］、能量最小轴、波峰数等四个特征。

①手势长度L

②手势能量E

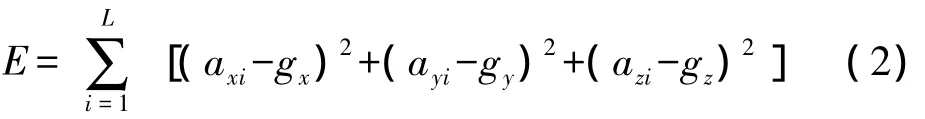
其中，L为手势长度，gx，gy，gz分别为重力加速度在设备 x，y，z轴分量;

③加速度能量最小轴:三轴手势能量最小轴;

④波峰数P

其中，Px，Py，Pz分别为设备 x，y，z轴加速度波峰数。为了可靠地计算波峰数，去除操作过程中环境噪声及用户抖动等偶然因素的影响，本文采用如图3所示方法。

图3 波峰数计算方法

首先遍历手势加速度数据，寻找其与横轴交点C1、C2、C3……，然后在相邻两交点间(C1C2、C2C3等)计算加速度最大值和最小值 P1、P2、P3……，若P1、P2……的加速度值大于波峰上限阈值或小于波峰下限阈值，则波峰数加1。

2.3 误动作去除

在使用过程中，传感器输出数据中包含了用户各种无意识的误动作，如将设备突然放下、将设备从一只手换到另一只手等。为了提高识别准确率，这些误动作必须被去除。而各类手势的加速度特征均具有一定的统计规律，如果不满足这些统计规律则视为误操作被去除。通过分析各类手势样本数据，本文得到3条统计规律，满足其中之一则为误操作:①L＜0.1 s，因为手势长度至少为0.1 s;②E＞1 500，因为手势能量最大为1 200左右;③300＜E＜1 000且P=0，因为能量处于300到1 000之间的翻转和甩动手势的波峰数不为0。

2.4 手势分类

为了提高分类准确率、简化分类算法，本文提出了如图4所示的三层决策树分类器。

图4 手势分类决策树

①分类器第1层:敲击类手势加速度小、持续时间短，手势能量远小于其他3类手势，因此利用手势能量分离敲击类手势;

②分类器第2层:手机等电子设备都为长方体，此处为清楚说明问题，设长方体长、宽、高分别对应X、Y、Z轴。翻转手势是绕X轴的转动，能量主要集中于Y、Z轴，因此X能量最小;而甩动类和晃动类手势中X轴能量在三轴中不可能最小。因此利用X轴能量最小可分离出翻转类手势。

③分类器第3层:对于甩动类和晃动类手势，由于个体之间的差异，单独使用手势长度、能量、波峰数等特征都不能达到较高的分类准确率。因此，本文结合这3个特征利用Fisher分类函数［13］来分类甩动类和晃动类。通过训练样本得到的Fisher分类函数为 f=47L+59E+108P－25690，如果 f＞0则为甩动类，f＜0则为晃动类。在分类函数中波峰数的系数最大，可以看出波峰数在甩动类和晃动类手势的分类中起主要作用，因为波峰数是这两类手势在运动学上的本质区别(如图5)。

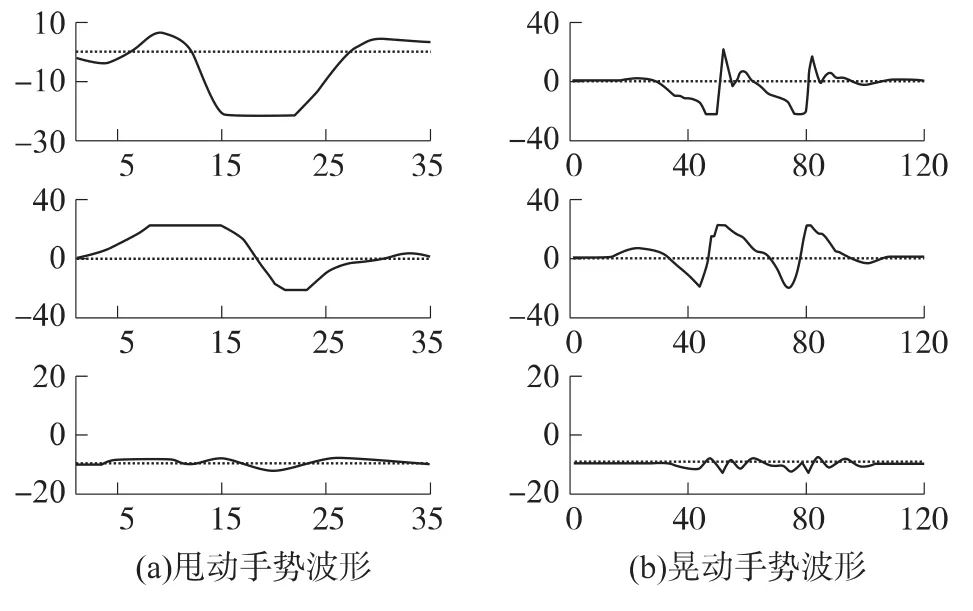
图5 不同手势波形

2.5 各类手势的识别

2.5.1 敲击次数识别

敲击类手势的加速度体现出冲击性，但敲击设备不同平面时，冲击特性在设备各轴上的显著程度不同。为了保证敲击次数识别的准确性，本文利用J=(|axi－axi－1|+|ayi－ayi－1|+|azi－azi－1|)来识别敲击次数。如图6所示，波形上升沿与次数识别阈值的交点数即为敲击次数。

图6 敲击次数识别

但是用户很多无意识的动作会被分类到敲击类中，如突然的抖动、将设备突然放下或拿起等。通过分析敲击类手势的特征量样本，本文提出了以下3条准则以去除敲击类手势中的误动作:

①每次敲击持续时间(如图 6，A2－A1，B2－B1，C2－C1)在0.1 s到0.2 s之间;

②相邻两次敲击间隔时间(如图 6，B1－A1，C1－B1)大于 0.15 s，因为用户不可能在 0.15 s内完成两次敲击;

“您的疼痛有所改变吗？”我低头询问着上周因工厂工伤，经历八小时手术的44岁病患目前的康复情况，如同往常的无数个清晨一样，我正带着四五位住院医师巡查骨科的各个病房。

③手势起点前0.3 s内的加速度标准差小于0.1 m/s2。因为敲击手势起点前的加速度是相对平稳的，而用户的无意识抖动等误动作的起点前加速度波动较大。

2.5.2 翻转手势识别

本文仅定义了逆时针翻转，因为顺时针翻转对用户而言很不方便，违反了手势定义的原则。因此翻转类手势的识别较为简单，当手势被分类为翻转后则完成识别。

2.5.3 甩动及晃动方向识别

加速度的变化规律被用于甩动及晃动方向的识别。用户坐标系与设备坐标系如图7所示，由于传感器输出的是设备局部坐标系(oxyz)中的加速度，加速度变化规律会随着设备姿态的不同而改变，但用户坐标系(OXYZ)中相同方向的甩动或晃动手势的加速度变化规律始终保持不变。因此，本文通过结合加速度计和陀螺仪得到设备姿态信息，将设备局部坐标系中的加速度转换到用户坐标系后，再对手势方向进行识别。

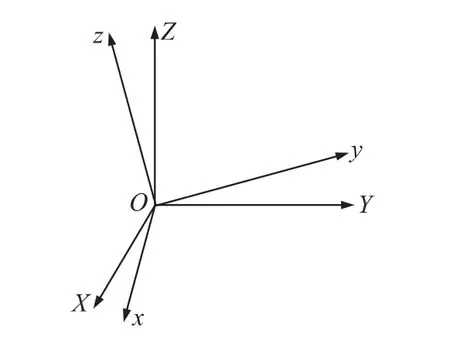
图7 用户坐标系(OXYZ)与设备坐标系(oxyz)

在设备姿态计算中，首先利用手势起点前设备x，y，z轴的重力加速度分量获得设备初始姿态［14］，其中倾斜角θ和横滚角γ的计算如式(4)和式(5)所示。

对于航向角φ，其初值可设为0，因为本文仅仅是将加速度数据转换到用户坐标系下，而非地球全局坐标系。

本文采用四元数 q=(q0，q1，q2，q3)来表示空间转动。通过初始姿态，利用式(6)可以得到四元数初值［14］:

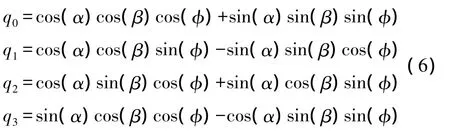
其中，α=φ/2，β=θ/2，φ=γ/2。由于表征旋转的四元数必须是规范化四元数，因此要对四元数初值做归一化处理，即是使四元数满足q20+q21+q22+q23=1［14］。

在姿态更新中，本文采用旋转不可交换性误差较小的等效三子样旋转矢量法更新四元数并得到各姿态更新点的坐标转换矩阵［15］，如式(7)

利用坐标转换矩阵CRb，根据式(8)便可以得到用户坐标系下去掉重力加速度后的手势加速度。

其中，下标R表示用户坐标系下的加速度，下标b表示设备坐标系下的加速度，坐标转换后的甩动手势加速度波形如图8所示。

实际上，甩动及晃动手势是绕用户手腕的圆周运动。在用户坐标系OXYZ中，当用户左右甩动或晃动时，Y轴为切向轴;当用户上下甩动或晃动时，Z轴为切向轴。同时甩动手势是一先加速后减速的运动，当甩动方向相反时，加速或减速的方向将相反。因此甩动方向可通过切向轴上加速度加减速方向进行识别。但是算法首先需要判断甩动发生在Y轴或是Z轴上，本文采用 Y轴和 Z轴的加速度平均幅值［2］AM(Average Magnitude)的相对大小判断甩动发生轴。

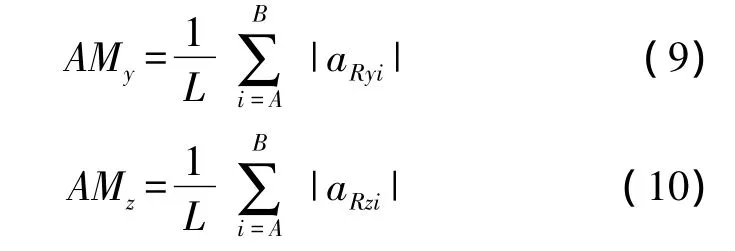
其中，aRyi、aRzi分别为用户坐标系下Y轴和Z轴手势加速度，A、B分别为手势起点和终点，L为手势长度。

对比图8(a)、8(b)、8(c)和8(d)可知，左右甩动时Y轴加速度幅值比Z轴大;上下甩动时Z轴加速度幅值比Y轴大。因此如果AMy＞AMz，则甩动发生在Y轴;如果AMz＞AMy，则甩动发生在Z轴。

图8 坐标转换后甩动手势加速度波形

由于本文仅定义了上下晃动和左右晃动，因此晃动方向的识别更为简单，仅利用Y轴和Z轴的加速度平均幅值相对大小即可识别晃动方向。如果AMy＞AMz则为左右晃动;如果AMz＞AMy则为上下晃动。

3 实验结果

为了测试算法的有效性和对个体差异的适应性，本文挑选了15名实验者并要求以他们习惯的方式和力度操作各个手势及常见误操作各100次。实验结果表明算法达到了95.2%的准确率，具体识别统计结果如表2所示，其中G1～G10分别代表单击、双击、三击、翻转、向左甩动、向右甩动、向上甩动、向下甩动、左右晃动、上下晃动，竖排G1～G10为输入手势，横排G1～G10为识别结果。

表2 实验统计结果

在识别算法中，传感器数据采样频率为100 Hz。当截取到手势数据后，手势识别能在下次采样之前顺利完成，由此可知手势识别时间小于0.01 s。

4 结论

本文通过提取不随个体差异变化的加速度特征量及变化规律对手势进行识别，因而方法简单有效，对个体差异适应性强。并且结合陀螺仪进行加速度数据坐标转换，取消了DTW和HMM方法对设备姿态的限制，实现了任意姿态下的手势操作。但在本文目前的研究中，陀螺仪并未得到充分利用，仅辅助用于加速度数据坐标转换。在今后的进一步研究中，可从陀螺仪数据中提取特征信息并结合加速度特征进行手势分类和识别，从而进一步提高识别准确率。

［1］ Eun-Seok Choi，Won-Chul，Sung-Jung Cho.Beatbox Music Phone:Gesture Based Interactive Mobile Phone Using a Tri-Axis Accelerometer［C］//IEEE International Conference on Industrial Technology，Hong Kong，2005:97－102.

［2］ Min Jun-Ki，Choe Bongwhan，Cho Sung-Bae.A Selective Template Matching Algorithm for Short and Intuitive Gesture UI for Accelerometer-Builtin Mobile Phones.IEEE Second World Congress on Nature and Biologically Inspired Computing［C］//Fukuoka，2010:660－665.

［3］ Ahmad Akl，Shahrokh Valaee.Accelerometer Based Gesture Recognition Via Dynamic-Time Warping，Affinity Propagation ＆ Compressive Sensing［C］//IEEE International Conference on Acoustics Speech and Signal Processing，Dallas TX，2010:2270－2273.

［4］ 荆雷，马文君，常丹华.基于动态时间规整的手势加速度信号识别［J］.传感技术学报，2012，25(1):72－76.

［5］ Sanna Kallio，Juha Kela.Online Gesture Recognition System for Mobile Interaction［C］//IEEE InternationalConference on Systems，Man and Cybernetics，Hong Kong，2003:2070－2076.

［6］ 李国峰，王锦，张勇，等.基于MEMS加速度传感器的智能输入系统［J］.传感技术学报，2009，22(5):643－646.

［7］ 梁秀波，张顺，李启雷，等.运动传感驱动的3D直观手势交互［J］.计算机辅助设计与图形学学报，2010，22(3):521－533.

［8］ 孔俊其，王辉，张广泉.基于加速度识别的姿态交互研究［J］.苏州大学学报(工科版)，2009，29(2):23－27.

［9］ 胡友树.手势识别技术综述［J］.科技论坛，2005，2:42－43.

［10］ Jiho Choi，Kyohyun Song，Seongil Lee.Enabling a Gesture Based Numeric Input on Mobile Phones［C］//IEEE International Conference on Consumer Electronics.Xi’an，2011:151－152.

［11］ Yuan Tao，Wang Ben.Accelerometer Based Chinese Traffic Police Gesture Recognition System［J］.Chinese Journal of Electronics，2010，19:270－274.

［12］ Yang Jhun-Ying，Wang Jeen-Shing，Chen Yen-Ping.Using Acceleration Measurement for Activity Recognition:An Effective Learning Algorithm for Constructing Neural Classifiers［J］.Pattern Recognition Letters，2008，29:370－388.

［13］边肇祺，张学工.模式识别(第二版)［M］.北京:清华大学出版社，2000:84－90.

［14］ Wang Jeenshing，Hsu Yuliang，Liu Jiunnan.An Inertial-Measurement-Unit-Based Pen with a Trajectory Reconstruction Algorithm and its Applications［J］.IEEE Transactions on Industrial Electronics，2010，57:3508－3521.

［15］ 秦永元.惯性导航［M］.北京:科学出版社，2006:305－354.