通过PVDF阵列测量体积位移的实验研究*

毛崎波

(南昌航空大学飞行器工程学院，南昌330063)

近几年来，压电智能材料(Piezoelectric Smart Material)特别是具有密度低、机械韧性好、可塑性强等优点的高分子压电薄膜PVDF(Polyvinylidene Fluoride)作为压电式传感器在结构声有源控制ASAC(Active Structural Acoustic Control)中的应用越来越引起关注[1－6]。由于振动结构的声功率为其表面法向速度的函数，表面法向速度的分布不同对声功率的贡献不同，所以合理的压电式传感器应该只测量对声辐射起主要贡献的结构振动。最近有学者提出通过抵消体积位移(Volume Displacement)设计ASAC系统，并对压电式体积位移传感器的设计方法进行了理论和实验研究[7－9]。这一方法的主要特点是利用模态的正交性得到特定形状的PVDF传感器形状，本文称之为“模态方法”。但是随着研究的深入，发现这种传感器设计方法存在如下问题难以解决:对于一种边界条件，就需要一种特定形状的PVDF传感器，边界条件的变化有可能使所设计的PVDF传感器的输出有很大的误差。PVDF薄膜的形状有可能很复杂，难以加工。

[10－13]提出了另一种模态传感器的设计方法，其基本思路为通过在振动结构表面上布置一组相同形状的矩形PVDF薄膜阵列，然后通过设计这组PVDF阵列的加权系数，测量振动结构的体积位移或声辐射模态。在此前发表的论文中，作者对此进行了大量的理论和实验研究[9－11，14－16]。进一步的研究表明通过这种方法所设计的PVDF薄膜并不需要覆盖整个结构的表面。但是这种方法的基本思想还是利用模态的正交性，所以在确定PVDF传感器的加权系数时必须预先解得结构的结构模态(振型函数)。

为了解决这些问题，本文以一未知边界条件的振动梁为例，提出通过测量 PVDF阵列中各个PVDF薄膜与激励力之间的频率响应函数，并结合伪逆方法和Tikhonov正则化方法设计PVDF阵列的加权系数，从而得到所需的体积位移。

1 基本理论

假设有一镶嵌在无限障板中的振动梁，长度为Lx，宽度为 Ly，厚度为 h。根据参考文献[7，10]可知，体积位移D为振动梁表面法向位移w(x)在整个梁表面上的积分，即

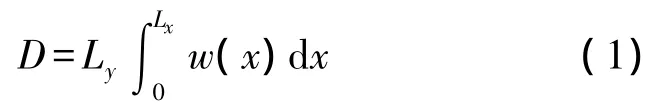
从声辐射模态理论可知，体积位移与第1阶声辐射模态的幅值成正比，在低频时第1阶声辐射模态对声功率起主要贡献[3－4]。Berry[17]进一步指出，当作用在梁上激励力的无量纲频率k·Lx≪1时(其中k为波数，k=ω/c0，ω为激励力频率，c0为声速)，声功率W可表示为

式中ρ0为空气的密度。

从式(2)可知，低频时梁的声功率与体积位移有直接关系。如果抵消了体积位移，就能使振动结构低频时的声功率明显降低。

2 PVDF传感器的设计

考虑在振动梁上均匀布置N块同样形状的矩形PVDF薄膜，如图1所示。假设第n个PVDF的其输出电荷为Qn，为了测量各阶模态坐标，我们通过对每个PVDF设计不同的加权系数，其基本思路如图2所示。从图2中可以看出，经过加权后，这组PVDF传感器的输出为

式中:Wn表示第n个PVDF传感器未知的加权系数。

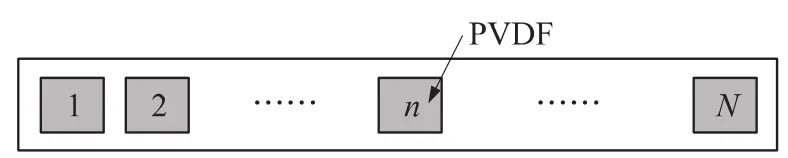
图1 PVDF示意图

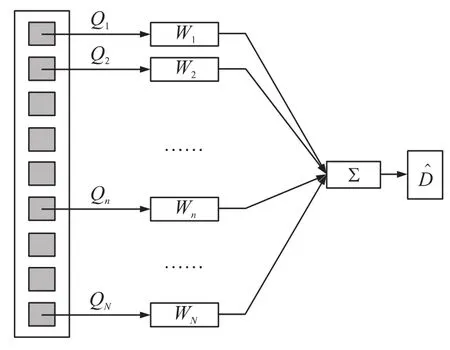
图2 通过PVDF阵列测量体积位移示意图

下面的任务是如何设计恰当的加权系数W使得经过加权后这组PVDF阵列的输出电荷 ^D等于体积位移D。

考虑到在实际工程应用中，一般情况下振动梁的边界条件或模态信息为未知。所以我们无法通过传统的模态方法[10－13，18]设计 PVDF 阵列的加权系数。为此我们提出伪逆方法设计PVDF阵列的加权系数，首先假设在一定频率范围内，通过一已知激励力下的体积位移D(ω)，并测量到该激励力与PVDF薄膜之间的频率响应函数Gn(ω)。

由式(3)可知，通过PVDF测量的体积位移D=^D可以表示为频率响应函数Gn(ω)和相应PVDF加权系数Wn的线性组合，即

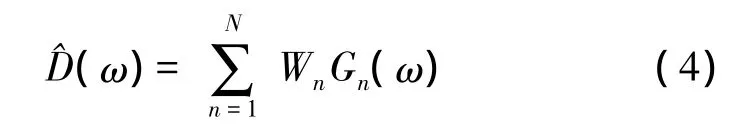
假设在式(4)中选取L(L＞N)个频率，则式(4)可以进一步表示为矩阵形式，即

式中:G矩阵的(l，n)元素为第n个PVDF在频率为ωl时的输出电荷。G和为复数矩阵，而W为实向量。

把式(5)代入式(6)得

从式(7)可知，可以定义误差准则J为

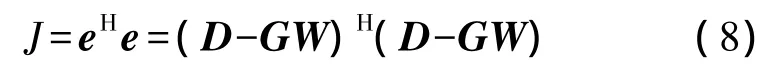
可以通过最小化式(8)即可得到PVDF阵列的加权系数向量W。注意到式(8)中WHGHGW=DHD=|D|2＞0，所以矩阵GHG为正定。式(8)为标准Hermitian二次方形式，具有唯一的最小值。根据线性均分优化理论，可以得到最优解:

式中:G+=[GHG]－1GH为G矩阵的伪逆。上标 H表示复共轭转置。

通过式(9)直接求解加权系数向量W存在的主要困难在于无法保证矩阵G不是病态的，有可能导致G矩阵中的测量误差在计算过程中被非线性放大，使得通过式(9)得到的加权系数偏离精确解。所以本文引入Tikhonov正则化方法求解方程(8)，Tikhonov正则化的基本思路是在式(8)的误差准则中加入一额外的约束，式(8)中的误差准则重新表示为[19－21]

式中:α为正则化参数(正实数)。在未知测量误差的情况下，可以通过广义交叉验证[18]GCV(Generalized Cross-Validation)方法确定正则化参数α，即

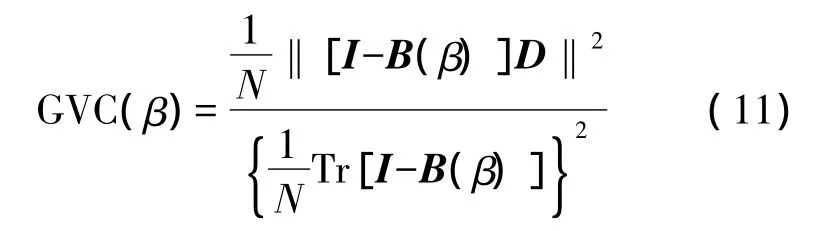
式中:Tr表示括号内矩阵的对角元素之和，B(β)=GT(GGT+αI)－1。

由参考文献[19－21]可知，式(10)的最优解为

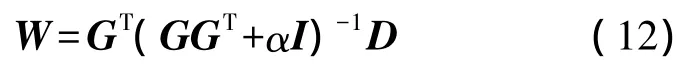
这样通过式(12)就可得到测量体积位移的PVDF阵列加权系数W。需要指出的是，本文方法不需要结构的模态信息或边界条件。还需要指出的是，只要把PVDF的电流信号作为输出，就可以测量体积速度[9]。

3 实验研究

为了验证本文的设计方法，取一铝梁长Lx=500 mm，宽Ly=40 mm，厚h=3.3 mm进行实验研究。通过在梁上均匀粘贴N=10块相同形状的矩形PVDF薄膜作为传感器测量该粱的体积位移，实验装置如图3所示。实验测量的前7阶固有频率如表1所示，在表1中同时列出了该梁在两端简支和两端固定的前7阶固有频率的理论值。从图2和表1可以发现，实验装置中振动梁的边界条件介于简支和固定之间。PVDF传感器的物理参数如表2所示。

图3 实验照片

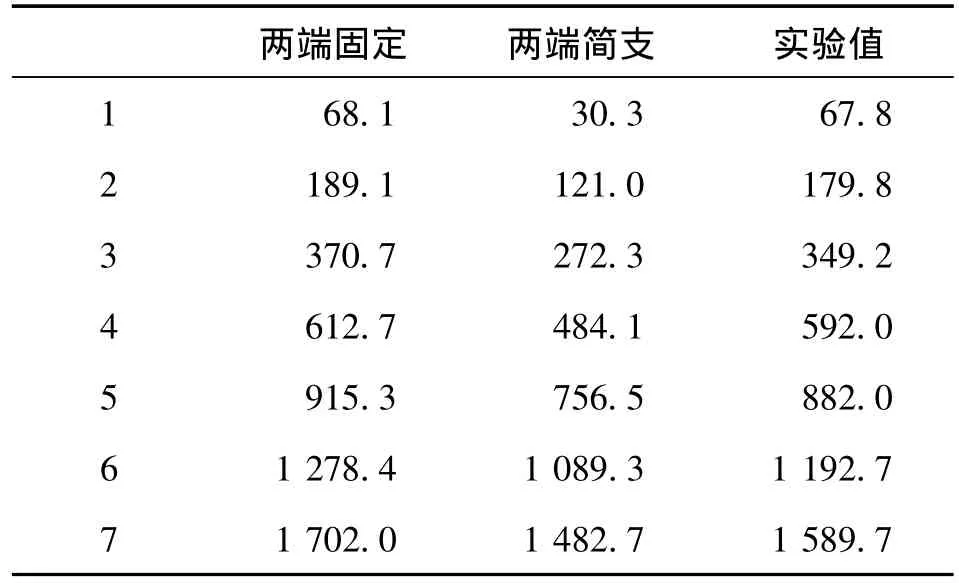
表1 实验梁前9阶固有频率(Hz)

表2 PVDF传感器的物理参数

实验中，用一悬挂激振器作为外部力源位于xd处，通过PCB力传感器(型号:208A04)测量输入力，B＆K Pulse动态分析仪进行正弦扫频(Sweep-Sine)，通过功率放大器驱动激励器，频率范围从5 Hz到2 000 Hz。首先外部力源位于xd=125 mm处，测量输入力和PVDF薄膜的传递函数G(ω)。并把梁均匀分成25个测量点，通过加速度计(型号:PCB333B31)逐点测量输入力和各测量点位移之间的传递函数 H(ω)。把式(1)进行离散化[5，8]，在 xd位置下幅值1 N的点力激励时的体积位移可表示为:

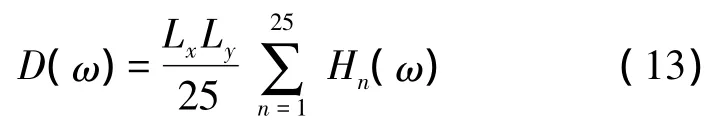
把测量的PVDF传递函数G(ω)和通过式(13)计算得到的体积位移D(ω)代入式(12)，可以得到PVDF阵列的加权系数W。图4表示根据式(12)得到的PVDF加权系数直方图。图5表示通过加速度计测量得到的体积位移与通过PVDF阵列得到的实验结果比较。从图5可以发现，体积位移在偶数阶(2，4和6)模态均出现较大的峰值，这表明实验中梁两端的边界条件并非简单固定或简支。这意味着本文的PVDF阵列设计方法可用于任意边界下振动梁体积位移的测量。

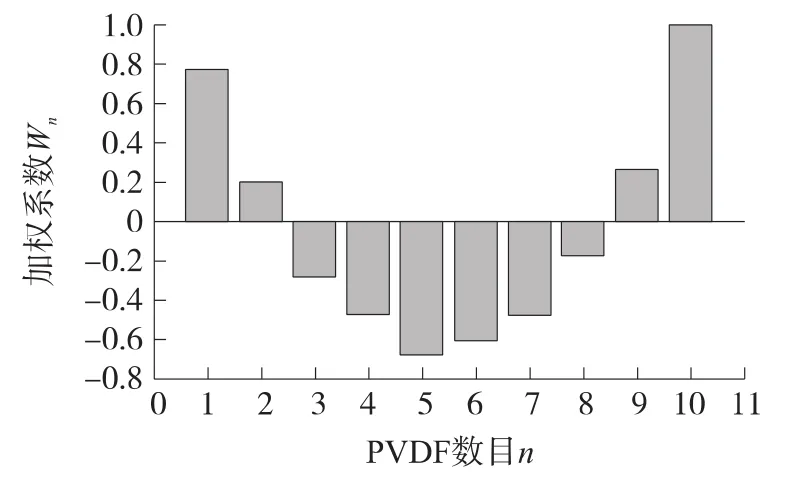
图4 PVDF传感器的加权系数Wn

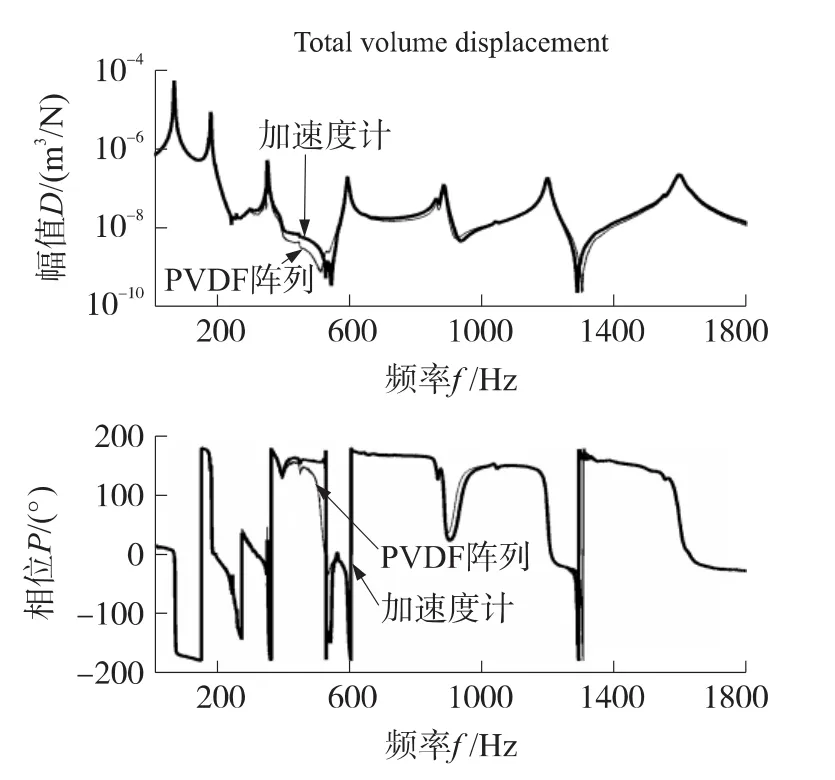
图5 分别通过PVDF阵列和加速度计测量体积位移幅值和相位(激励力位于xd=125 mm)

由于PVDF阵列的加权系数与外激励力性质(如激励力类型、频率以及位置等)无关[8－11]，所以可以通过该加权系数通过式(4)计算任意激励下体积位移。图6表示当激励力移动到xd=330 mm时，通过图4所示的PVDF加权系数得到的体积位移与实际体积位移(通过加速度计测量得到)之间的比较。从图5和图6中可以发现，在大部分频率范围内，PVDF阵列输出与加速度计测量的体积位移吻合得很好。与作者之前通过模态方法结合PVDF阵列实验测量的声辐射模态[7，9](第一阶声辐射模态幅值与体积位移成正比)相比，本文PVDF阵列的实验精度大为提高。这是由于模态方法必须预先知道实验梁的模态信息，但是实验中梁的边界条件与理想情况(一般假设为简支或固定)会有一定误差。这些边界条件的误差会导致PVDF传感器的测量误差就随着频率提高而增加[14－16]。而本文直接通过伪逆方法结合Tikhonov正则化设计PVDF阵列体积位移传感器，不需要振动结构任何模态或边界条件信息。从而使得本文的PVDF加权系数以及测量结果更加精确。

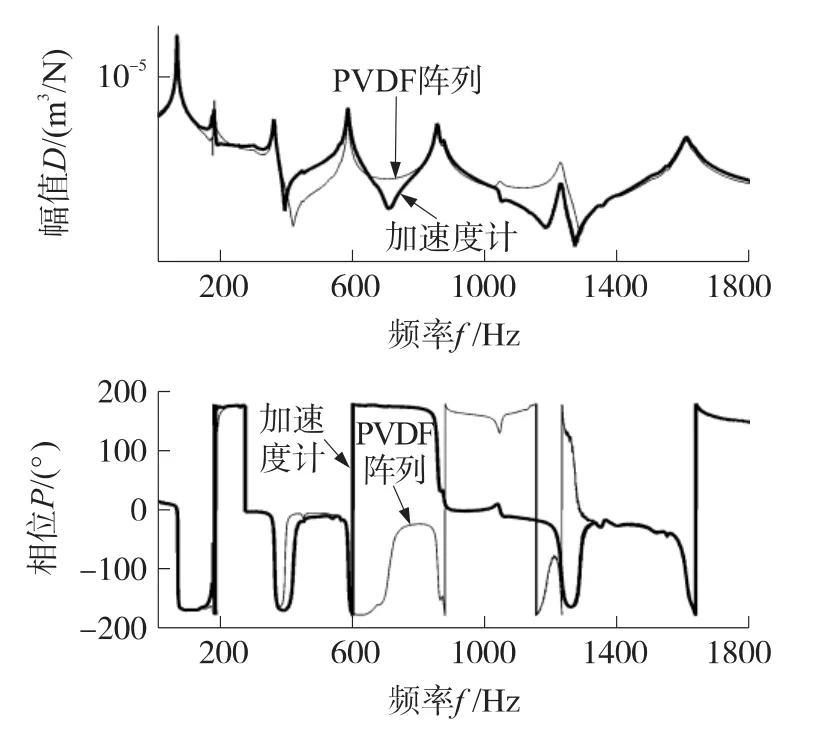
图6 分别通过PVDF阵列和加速度计测量体积位移幅值和相位(激励力位于xd=330 mm)

4 结束语

本文通过一组矩形PVDF薄膜测量未知边界条件下振动梁的体积位移。这种方法的优点在于只需要测量一组在某一激励力下PVDF阵列的频率响应函数以及在该激励力下的体积位移，就可以通过伪逆方法结合Tikhonov正则化得到PVDF阵列的加权系数，该PVDF加权系数可用于计算任意激励下的体积位移。本文方法的另一个重要优点是不需要任何模态信息或边界条件信息。实验结果表明本文方法的测量精度比模态方法[9－13]大为提高。

参考文献:

[1]Gardonio P，Lee Y S，Elliott J S.Analysis and Measurement of a Matched Volume Velocity Sensor and Uniform Force Actuator for Active Structural Acoustic Control[J].Journal of the Acoustical Society of America，2001，110(6):3025－3031.

[2]Henrioulle H，Sas P.Experimental Validation of a Collocated PVDF Volume Velocity Sensor/actuator Pair[J].Journal of Sound and Vibration，2003，265(13):489－506.

[3]毛崎波，姜哲.通过压电式传感器进行简支梁声辐射有源控制[J].声学学报，2001，26(6):527－531.

[4]毛崎波，徐柏龄.通过压电高分子薄膜设计声辐射模态传感器[J].声学学报，2003，28(3):262－266.

[5]陈卫东，董艳茹，朱奇光，等.基于PVDF的三维机器人触觉传感器有限元分析[J].传感技术学报，2010.23(3):336－340.

[6]揭琳锋，朱晓锋，王国林，等.PVDF的大拉伸变形测试机理研究[J].传感技术学报，2010.23(6):896－898.

[7]Marcellin B Z，Naghshineh K，Kamman J W.Narrow Band Active Control of Sound Radiated from a Baffled Beam Using Local Volume Displacement Minimization[J].Applied Acoustics，2001，62(1):47－64.

[8]Zahui M，Wendt R.Development of Local Volume Displacement Sensors for Vibrating Plates[J].Journal of the Acoustical Society of America，2004，116(4):2111－2117.

[9]Mao Q，Xu B，Jiang Z，et al.A Piezoelectric Array for Sensing Radiation Modes[J].Applied Acoustics，2003，64:669－680.

[10]Mao Q，Pietrzko S.Measurements of Local Volume Displacement Using a Piezoelectric Array[J].Acta Acustica united with Acustica，2006，92(4):556－566.

[11]毛崎波，蔡忆昔，李小华.通过压电式传感器阵列测量简支梁的声辐射模态[J].中国机械工程，2009，20(9):1169－1172.

[12]Francois A，Man P D，Preumont A.Piezoelectric Array Sensing of Volume Displacement:A Hardware Demonstration[J].Journal of Sound and Vibration，2001;244(3):395－405.

[13]Preumont A，Francois A，Man P D，et al.Spatial Filters in Structural Control[J].Journal of Sound and Vibration，2003，265(1):61－79.

[14]Mao Q，Pietrzko S.Design of Shaped Piezoelectric Modal Sensor for Beam with Arbitrary Boundary Conditions by Using Adomian Decomposition Method[J].Journal of Sound and Vibration，2010，329:2068－2082.

[15]Mao Q.Design of Shaped Piezoelectric Modal Sensors for Cantilever Beams with Intermediate Support by Using Differential Transformation Method[J].Applied Acoustics，2012，73(2):144－149.

[16]Mao Q，Pietrzko S.Design of Shaped Piezoelectric Modal Sensor for a Type of Non-Uniform Beams Using Adomian-Modified Decomposition Method[J].Journal of Intelligent Material Systems and Structures，2011，22(2):149－159.

[17]Berry A.Advanced Sensing Strategies for the Active Control of Vibration and Structural Radiation[J].Noise Control Engineering Journal，2001，49(1):54－65.

[18]Lee C K，Moon F C.Modal Sensors/Actuator[J].Journal of Applied Mechanics，1990，57(2):434－441.

[19]Nelson P A，Yoon S H.Estimation of Acoustic Source Strength by Inverse Methods:Part 1，Conditioning of the Inverse Problem[J].Journal of Sound and Vibration，2000，233(4):643－668.

[20]Yoon S H，Nelson P A.Estimation of Acoustic Source Strength by Inverse Methods:Part 2，Experimental Investigation of Methods for Choosing Regularization Parameters[J].Journal of Sound and Vibration，2000，233(4):669－705.

[21]Yoon S H，Nelson P A.A Method for the Efficient Construction of Acoustic Pressure Cross-Spectral Matrices[J].Journal of Sound and Vibration，2000;233(5):897－920.