一种基于自适应陷波器的科氏流量计频率解算新方法*
2012-06-12任建新暴苗刚孙慧芳
任建新 ,暴苗刚,张 鹏,孙慧芳
(1.西北工业大学自动化学院,西安710129;2.西安东风机电有限公司,西安710068)
科氏质量流量计是美国Micro Motion公司于1977年首先研制成功的一种基于处于旋转系中的流体在直线运动时产生与质量流量成正比的科里奥利力原理的新型质量流量计,可以高精度地测量流体质量。其问世后很短的时间内,就以优越的性能在工业界内赢得了很好的信誉。经过二十多年的发展,科氏流量计在性能和规格上逐渐完善,成为当前发展最为迅速的流量计之一。科氏流量计是利用流体流过振动的振动管产生的科氏力,使振动管发生扭转,从而导致两个传感器的输出信号之间产生相位差,通过测出相位差和信号频率即可得到流体质量流量[1]。而测量管输入段与输出段两路信号间相位差的精确测量首先要精确测得这两路信号的频率。因此用科氏流量计测量流体参数的关键技术之一是精确测量上述两路信号的频率。
现有基于自适应陷波器的方法由于可以根据被处理信号的特点,自动调整自身模型参数,使其幅频特性的陷波频率收敛到信号基频处,并可由陷波器的参数求出基频,实现频率的实时测量与跟踪而倍受国内外研究者的关注[2-5]。文献[6]所采用的基于IIR格型滤波器的自适应陷波器(下文简称格型自适应陷波器),其计算复杂、长时间持续跟踪能力较差。文献[7-8]采用一种结构和算法均比较简单的基于简化梯度算法实现的格型自适应陷波器(下文简称简化格型自适应陷波器),可以较好地跟踪信号频率,但须预先知道信号的初始频率。本文在对格型自适应陷波器、简化格型自适应陷波器两种典型自适应陷波器的性能分析比较的基础上,提出一种采用基于IIR格型滤波器的自适应陷波器和基于简化梯度算法实现的格型自适应陷波器交替跟踪信号频率变化的有效新方法,利用MATLAB对信号模型及实测数据进行仿真,对仿真结果与运用格型自适应陷波器频率解算方法进行比较分析。
1 科氏流量计信号模型的建立
信号模型的建立是为了模拟现场使用时的实际信号,科氏流量计传感器两路信号在理想状态下均为频率和幅值相等的正弦信号。在测量过程中,由于受到流速、密度和温度等因素影响,振动管的频率、幅值均会发生变化,为此合肥工业大学徐科军提出时变信号模型[5]。但是在流量计实际应用中发现,对于同一种流体在不同情况下,温度变化对振动管的固有频率影响比较严重,但是可以通过算法进行补偿,其他情况对频率的影响很小,相对于现阶段的测量精度可以忽略不计[9],因此本文仍然使用时不变信号模型。
实际应用中噪声的带宽比较大,时间分布不确定,为此采用正弦信号与高斯白噪声的组合作为科氏流量计的信号模型[8],即:

其中:s(n)为有用信号,v(n)为噪声,f为信号频率,fs为采样频率,φ相位,σe为噪声水平,e(n)是均值为0,方差为1的高斯白噪声。
2 基于IIR格型滤波器的自适应陷波器
格型自适应陷波器是由cho[10]等人提出的,其由两级格型滤波器级联而成,是一种级联的全极点和全零点格型陷波器,其结构如图1所示,传递函数为:

式中k0可以运用格型FIR滤波器的自适应算法进行自适应调节,参数ρ决定陷波器陷阱的带宽,x(n)-y(n)即为除去噪音后的增强信号。
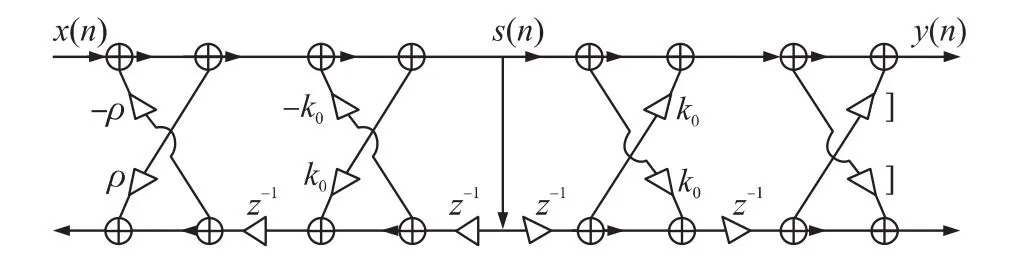
图1 格型IIR陷波器
Burg算法是较早提出的建立在数学基础上的AR系数求解的有效算法,其自适应调整过程如下:

其中:λ(n)为遗忘因子。
为保证陷波器稳定,k0必须在[-1,1]内,因此在算法中加入如式(4)的判断环节,以确保算法稳定。

式(5)相当于一个低通滤波器,对得到的k0(n)进行平滑处理,选取γ=0.5。
格型IIR陷波器的输出为:
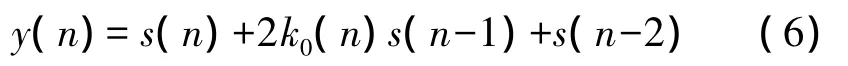
最后,x(n)-y(n)即为去除噪声后的增强信号,则信号的频率估计为^ω(n)=arccos(-k0(n))。
3 基于简化梯度算法实现的格型自适应陷波器
简化格型自适应陷波器的二阶传递函数为:

其中:β=cos(w0),w0为陷波频点;α应该等于或者稍微小于1,以确保系统稳定,α=[1-tan(BW/2)]/[1+tan(BW/2],BW为具有3 dB的衰减的陷波带宽。通过调节参数β和α实现对陷波频率和陷波带宽的独立调节,参数α越大,滤波器的陷波带宽越窄,滤波效果越好。该滤波器的格型结构图如图2所示,该结构的乘法与加法数量最少,使运算量得以简化[11]。
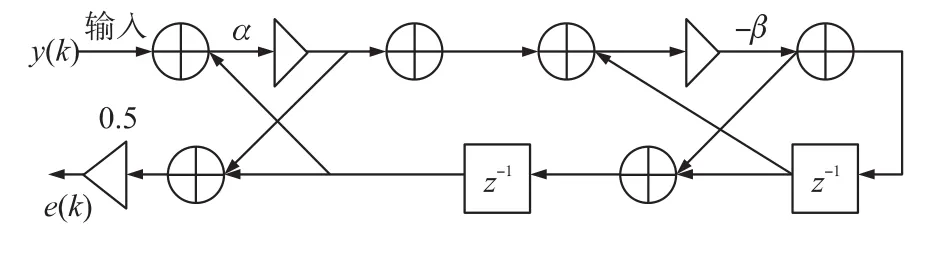
图2 简化格型自适应陷波器
如果将陷波带宽BW或α固定,即将极点到单位圆的距离固定,可获得稳定的自适应IIR滤波器。通过调节陷波频率参数β,可以跟踪信号频率的变化,其调节过程为[8]式(8)。其中:步长μ决定算法的收敛速度,μ越大,收敛速度越快,但会使得估计频率的波动增大。y(k)-e(k)是期望的信号。

4 一种频率解算的新方法
格型自适应陷波器检测信号的初始频偏范围大,收敛速度较快,短时间跟踪信号频率的随机变化精度较高,但是计算复杂,难以长时间持续跟踪信号频率的变化[12]。简化格型自适应陷波器计算简单、便于硬件实现,但是当检测信号未知时,难以兼顾收敛速度和频率跟踪精度,所以一般不单独使用。
经过上述对格型自适应陷波器、简化格型自适应陷波器两种典型自适应陷波器优缺点的比较分析后,提出一种用格型自适应陷波器和简化格型格型自适应陷波器交替跟踪信号频率变化的新方法:首先用格型自适应陷波器快速检测信号频率,待其接近收敛时简化格型自适应陷波器开始工作,格型自适应陷波器停止工作,由简化格型自适应陷波器独立跟踪信号频率直至结束。该方法针对格型自适应陷波器存在难以兼顾信号频率的收敛速度和长时频率跟踪精度的问题,综合利用了格型自适应陷波器收敛速度相对较快、短时频率跟踪精度较高和简化格型自适应陷波器计算简单、对硬件要求较低、能长时间高精度的跟踪信号频率。简化格型自适应陷波器可调节陷波参数,实现对信号的快速、持续精确跟踪,具有很强的灵活性和可调整性。
实现步骤如下:
(1)在信号初始频率未知的情况下,首先采用格型自适应陷波器快速检测信号频率;
(2)格型自适应陷波器频率跟踪算法接近收敛时,将计算到的信号频率作为简化格型自适应陷波器的初始陷波频率,此时简化格型自适应陷波器开始工作,格型自适应陷波器停止工作。
(3)简化格型自适应陷波器独立跟踪信号频率直至结束。在实际流量测量过程中,科氏流量计传感器信号频率的波动范围通常很小,一般不超过流量管振动频率的±0.01%[13],这种情况下本方法能够保证较高的跟踪精度。
5 仿真结果
5.1 参数值设定
弯管传感器的固有频率为20 Hz~300 Hz之间,相位差小于±4 Hz,单次仿真实验选择20 000个采样点,参数取值为:
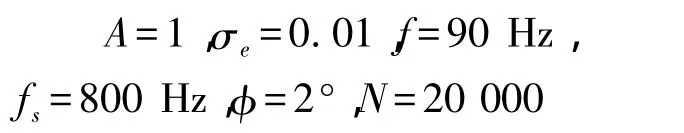
对于格型自适应陷波器主要参数是:ρ(0)=0.8,λ(0)=0.95,s(0)=0
对于简化格型自适应陷波器的主要参数:μ=0.000 02,α=0.90
本文方法中,格型自适应陷波器主要用于快速检测初始信号频率,交替点n的取值为3 500。
5.2 收敛性分析
图3为原始信号的时域图,图4和图5分别为经格型自适应陷波器和本文所述方法陷波滤波后的信号时域图,从图4可以看出经格型自适应陷波器滤波后经过6 000点以后才能稳定收敛,图5表明经本文方法陷波滤波后得到的增强信号在3 500点左右就能达到稳定收敛,收敛时间较短暂,得到的增强信号受收敛过程影响较小,去噪效果较好(下图横坐标单位都为点数n,纵坐标为Hz)。

图3 原始信号时域图
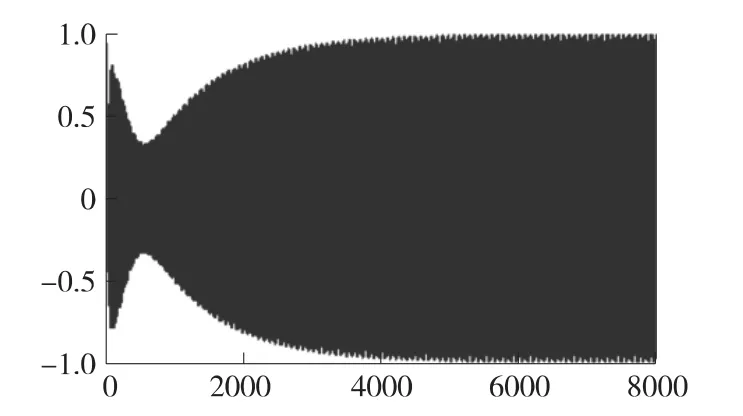
图4 经格型自适应陷波器滤波后的增强信号时域图

图5 经本文方法滤波后的增强信号时域图
5.3 频率跟踪误差分析
图6和图7分别为格型自适应陷波器和本文方法频率跟踪误差的曲线,由于简化格型自适应陷波器收敛之前,仍以格型自适应陷波器的跟踪频率作为估计频率,故图7从4 000开始。两图比较可以看出,格型自适应陷波器的频率跟踪的误差大约为0.006 8 Hz,而本文所述方法跟踪频率的误差小于±0.002 Hz,本文方法的整个过程的频率曲线较好的反应了频率的情况,本文方法跟踪精度比格型自适应陷波滤波器的更高,收敛速度更快,很好的兼顾了算法的收敛速度和频率跟踪精度。

图6 格型自适应陷波器的频率跟踪误差

图7 本文方法滤波后的频率跟踪误差
为更清楚的描述本算法的频率跟踪特性,分别计算两种方法的估计频率的均方误差,交替点前因用的都是格型自适应陷波器的估计频率,故只比较交替点以后的均方误差。
根据表1得到的误差值可知,本文方法信号跟踪频率均方误差相比格型自适应陷波器小,工作稳定性更好。

表1
综上所述,本文方法比格型自适应陷波器收敛更快,精度更高,稳定性更好,对信号的持续跟踪精度也比格型自适应陷波器高。
6 实验数据处理
为验证本方法的实用性,在科氏流量计上做采样实验,得到采样数据。取100 000个点,根据本文方法采用Matlab对实验数据进行处理。根据处理结果图8表明频率求解的误差在±0.002 Hz以内,优于一般科氏流量计的频率解算精度±0.005 Hz的要求,结果表明本文所述方法是行之有效的,有很好的实用性和经济价值。

图8 实验数据的频率跟踪误差
7 结束语
为解决格型自适应陷波器计算较为复杂,难以进行长时间持续跟踪信号频率变化的问题,本文采用了格型自适应陷波器与简化格型自适应陷波器交替跟踪信号频率的方法,格型自适应陷波器工作一段时间后停止,简化格型自适应陷波器独立工作,比单一采用格型自适应陷波器方法计算更为简单。仿真和实验结果表明,该方法把把格型自适应陷波器的检测初始频偏的范围大和简化格型自适应陷波器的计算简单、能长时间高精度跟踪信号频率结合起来,有效提高了收敛速度和持续的跟踪精度,相比格型自适应陷波器有很大优势和很强的实用性。
[1] 朱德祥.测量仪表原理与应用[M].上海:华东化工学院出版社,1992.
[2] 汪首坤,林波涛,王军政.自适应等精度频率测量方法与实现[J].传感技术学报,2007,20(2):346-349.
[3] 梁红,李志舜.几种自适应 IIR陷波器的复数算法及其应用[J].应用声学,2008,27(1):49-53.
[4] 刘立阳,张金成,吴中林.基于分布式动态簇结构的WSN自适应目标跟踪算法[J].传感技术学报2012,25(1):110-113.
[5] 储昭碧,张崇巍,冯小英.基于自适应陷波滤波器的频率和幅值估计[J].自动化学报,2010,36(1):60-66.
[6] 徐科军,倪伟,陈智渊.基于时变信号模型和格型陷波器的科氏流量计信号处理方法[J].仪器仪表学报,2006,27(2):596-601.
[7] Nishimuras Aloys M.A Lattice-Based Adaptive IIR Notch Filter and Its Application to FSK Demodulation[J].ISCAS,2000,3(5):586-589.
[8] Regalia P.An Improved Lattice-Based Adaptive IIR Notch Filter[J].IEEE Trans.Signal Processing,1991,39(9):2124-2128.
[9] 牛尔卓.科里奥利质量流量计数字解算及相关技术研究[D].西安:西北工业大学,2009.
[10]张贤达.现代信号处理[M].北京:清华大学出版社,2002.
[11] Regalia P A,Mitra S K,Vaidyanathan P P.The Digital All-Pass Filter:A Versatile Signal Processing Building Block[J].Proc.IEEE,1988,76(1):19-37.
[12]牛鹏辉,涂亚庆,张海涛.基于时变模型的科氏流量计信号处理方法与仿真[J].系统仿真学报,2008,20(6):1585-1588.
[13]李叶,徐科军,朱志海,等.面向时变的科里奥利质量流量计信号的处理方法研究与实现[J].仪器仪表学报,2010,31(1):8-14.
