高g光学微腔加速度计的结构设计*

王晓倩，李 鹏，孟祥然，徐鹏飞，冯薪霖，薛晨阳，闫树斌*

(1.中北大学仪器科学与动态测试教育部重点实验室，电子测试技术国家重点实验室，太原030051;2.山西大学物理电子工程学院，太原030006)

近年来基于MEMS技术的微惯性器件具有可靠性高、易于大规模集成、固有频率高等优点，集成和微加工技术广泛应用于构建大规模集成系统。针对惯性载荷场合测量的迫切需要，其加速度测量值可以高达104gn，这就要求加速度计不仅需要高的灵敏度，还要具有高的谐振频率与抗冲击能力。高g值加速度计主要用于高速运动载体在启动和着靶过程中速度变化的测量与控制，例如在航空航天领域以及导弹和侵彻引信的精确控制方面已经得到了广泛应用［1－6］。

微纳光波导与硅微机械传感结构相结合的MOEMS加速度传感器具有体积小、重量轻、功耗低、灵敏度高、动态范围大等特点，在军民用两方面如惯性系统、导弹系统、汽车安全、工业机器人和生物检测［7－8］等领域有着广泛的应用前景。文中所研究的是通过光弹效应并基于SOI(Silicon-On-Insulator)材料的高g值集成光学微结构加速度传感器［9］;通过对光学微结构和悬臂梁的尺寸进行优化设计分析，并运用ANSYS和FDTD软件模拟分析，得到的加速度计具有较高的灵敏度、谐振频率和较大的抗冲击能力。

1 加速度计原理概述

该加速度传感器的原理为在加速度作用下，结构受到的惯性力使悬臂梁发生弯曲，根据光弹效应，光在光波导和环形谐振腔倏逝场耦合时的传输特性发生变化;通过探测由于MEMS结构形变而引起的光学信号变化，可以得到高精度的悬臂梁位移变化，从而测定加速度值。其倏逝场耦合主要利用平面环形微腔和纳米光波导对光子的局域场效应，使光场主要以倏逝波形式沿波导表面传播，实现纳米光波导与环形微腔的高效耦合，耦合后的激光在环形微腔中经过谐振叠加，并以频率梳齿形式透射输出。

如图1(a)所示，该传感器主要由集成光波导和悬臂梁结构组成，悬臂梁的两端分别为基底和质量块，微结构位于悬臂梁与基底连接处。如图1(b)所示，当质量块受到加速度方向的惯性力时，悬臂梁发生位移形变，从而谐振腔的周长Lr和有效折射率Δneff发生较大的变化，环形微腔的微小位移对透射光谱的影响如式(1)所示［10］:

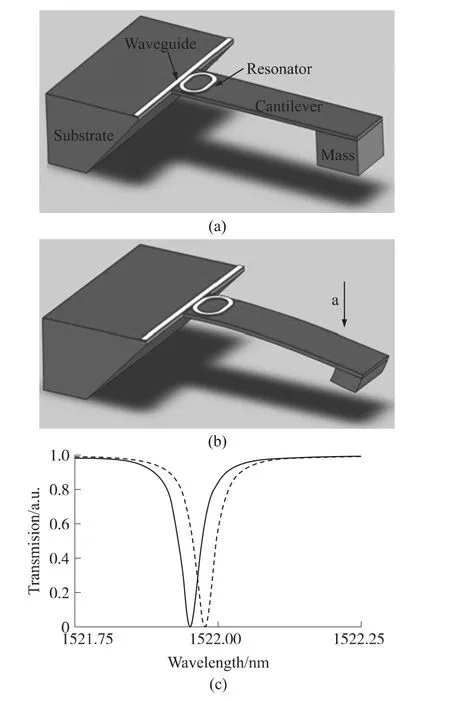
图1 传感器工作原理示意图

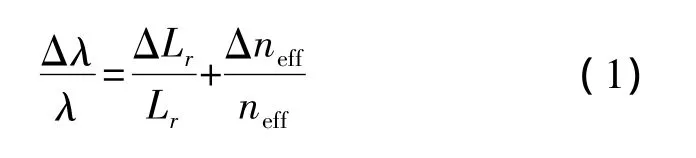
其λ表示微环谐振波长，Δλ表示波长偏移量如图1(c)所示。根据微环谐振腔在光压方向上的形变距离和透射光谱振幅的变化关系［11］:

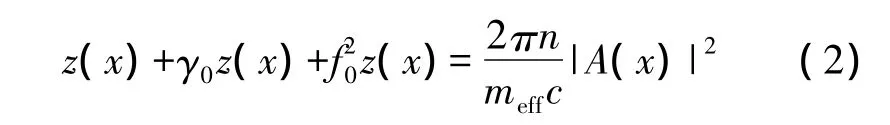
可观察到光场幅度的变化。其中z(x)表示微环谐振腔在光压方向上的微小位移变化，meff表示机械系统在光压方向上有效的振荡质量，f0表示机械本征频率，γ0表示机械阻尼固有系数，A(x)表示因为光压存在而缓慢改变的光场幅度，c/n表示光在环形腔中的速率。

当悬臂梁受到惯性力F时，悬臂梁发生弯曲，各点的应力与位移量的关系如式(3)所示:

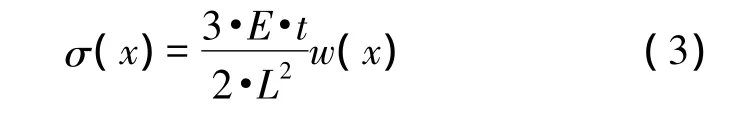
其中E表示悬臂梁的杨氏模量，t表示悬臂梁的厚度，L表示悬臂梁的长，w(x)表示在外力F作用下沿悬臂梁方向的位移量。根据光弹效应，有效折射率与应力的关系表示如下［12］:

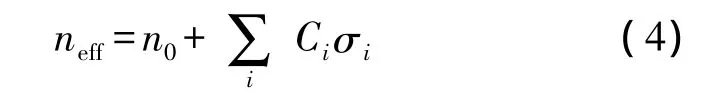
Ci表示光波导的光弹系数，σi表示微环腔所受到的压力。由式(4)可以看出，有效折射率依据材料的光弹系数和几何尺寸的变化而变化。其有效折射率的变化量为:

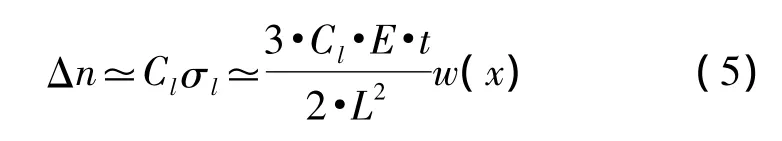
由于跑道形环形谐振腔各点所受压力不同，因此透射谱的偏移量为环形区各处相位的积累:

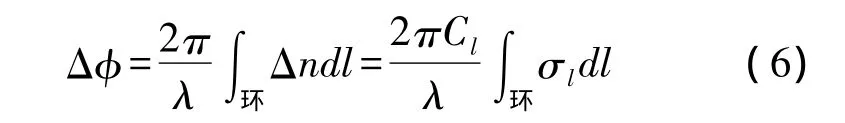
为了得到频谱较大的偏移量，根据式(6)，必须增加谐振腔长度和材料的光弹系数。

假设在加速度a下，跑道形环形谐振腔周长的变化量为ΔLr，根据光弹效应谐振腔折射率的变化量为Δneff，根据硅材料的性质，传感器的灵敏度为:

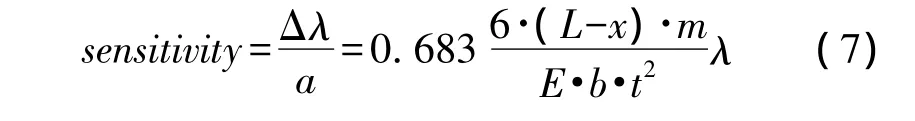
其中m为质量块的质量，x为谐振腔到悬臂梁固定端的距离。悬臂梁的谐振频率为［13］:

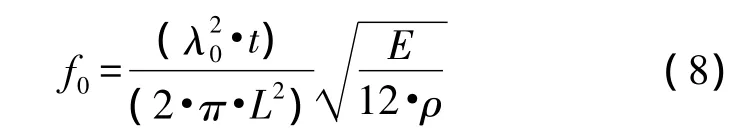
其中λ0表示一阶共振常数，ρ表示悬臂梁的密度。由式(7)～式(8)可以得到，当悬臂梁的长度增加厚度减少时灵敏度增加，而谐振频率降低。

GaAs，SiO2及Si广泛应用于集成光学微结构中，其材料属性如表1所示。

表1 材料属性参数表

从悬臂梁特性考虑，如图2所示，通过MATLAB仿真，在外力F作用时，相同结构条件下SiO2悬臂梁的形变量最大;从光学特性考虑，Si材料有更加优良的光学输出特性。根据光的全反射和倏逝波的产生传输条件，光波导的折射率必须大于衬底的折射率。综合上述特性，材料Si作为环形谐振腔，材料SiO2作为悬臂梁是最佳选择，此结构即是前文所述的SOI材料。

图2 结构相同，在外力F作用下，不同材料的形变量

2 跑道形环形谐振腔的结构设计

光在波导中以电磁波形式进行传输，当光能量集中在波导芯区时，电磁波在传输方向上以波导中心向外衰减，该波导中TE模的本征方程为:

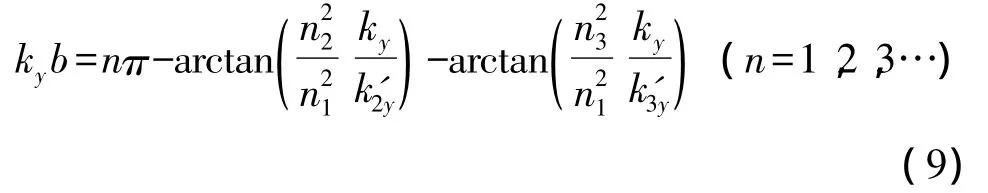
其中k'2y、k'3y分别表示光在覆盖层和衬底的衰减情况，ky表示传输方向上的波矢大小，n1表示波导折射率，n2表示波导覆盖层折射率，n3表示波导衬底折射率，k0=2π/λ表示真空中的波矢，λ表示传输光的波长。

光在波导中传输具有多种模态，为了实现光在微环谐振腔和光波导内的单模传输，需要对微环与光波导的参数进行合理设计，文中利用有效折射率法对其单模特性进行数值计算。波导位于SOI顶层其折射率n1=3.42，覆盖层为空气其折射率n2=1，衬底为二氧化硅其折射率n3=1.45，波长λ=1 550 nm。图3(a)为光波导模态传输曲线，m=0表示基模传输曲线，m=1表示一阶模传输曲线，m=2表示二阶模传输曲线，并由此可以得到当波导高度介于0.22 μm ～ 0.45 μm 时，光在波导中以单模形式传输。利用 Beamprop软件对高度 h=0.22 μm，宽度b=0.4 μm进行仿真，由图3(b)看到光完整地被局限在光波导中。

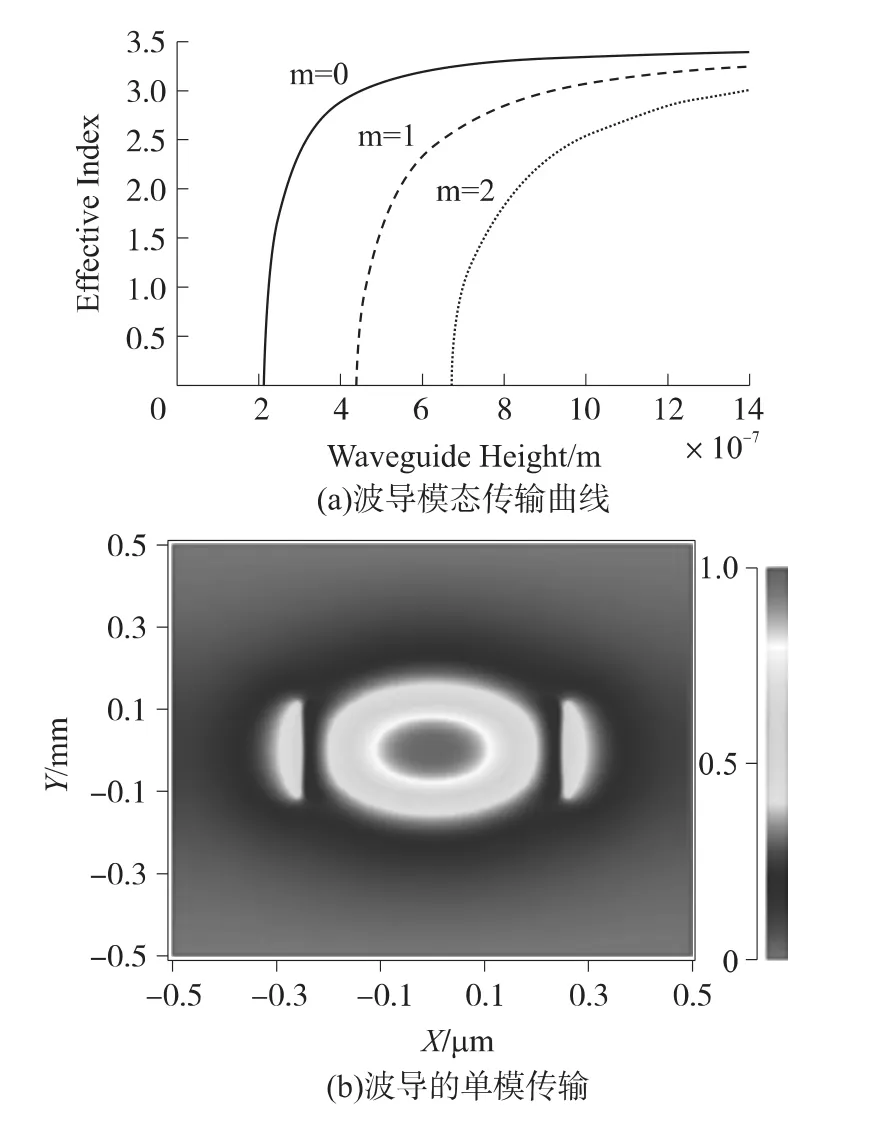
图3 波导模态传输曲线及波导中的单模光传输分布

微环形谐振腔是整个加速度计的核心部件，与系统灵敏度有着直接的关系。为了提高耦合效率、Q值和灵敏度，文中将环形谐振腔设计为跑道型，可以有效的增加耦合长度提高传感器的灵敏度。在倏逝场耦合中，耦合间距与耦合效率成线性关系，随着耦合间距的增加，耦合效率线性减弱。文中采用的耦合距离d=0.1 μm，并通过 FDTD仿真得到跑道形微环腔的尺寸，如图4所示，跑道形微环腔圆环的半径 R=4.6 μm，中间直跑道的长度 Lc=3 μm。

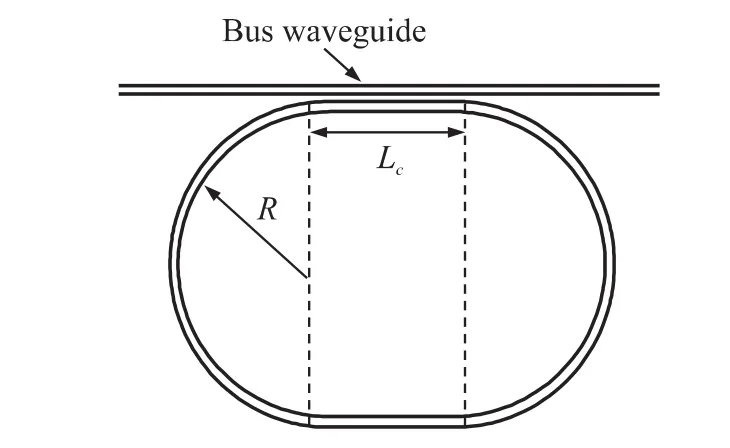
图4 跑道形微环谐振腔

3 悬臂梁的结构设计

悬臂梁是探测微小位移的重要结构，其结构有长方体、V形体等，本中采用等截面长方体悬臂梁，其测量原理就是根据牛顿第二定律，作用在物体上的惯性力F等于该物体的质量M与其加速度a的乘积。在加速度a的作用下，悬臂梁的挠度为:

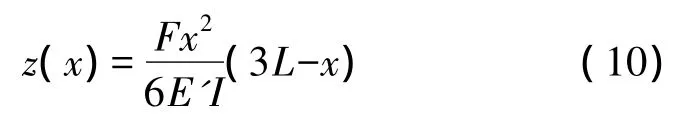
其中L 表示悬臂梁的长，E'=E/(1－ν2)，ν=0.17 表示二氧化硅的泊松比，I=wt3/12表示长方体等截面悬臂梁的惯性矩，t表示悬臂梁的厚度，w表示悬臂梁的宽度。如图5所示，利用MATLAB软件对悬臂梁的长、高分别进行仿真，可以得出悬臂梁越长位移越大，越厚位移就越小。根据跑道形微环腔的总长度为12.2 μm，设定悬臂梁的长宽高分别为100 μm、15 μm、1 μm，质量块的长宽高分别为25 μm、15 μm、25 μm。

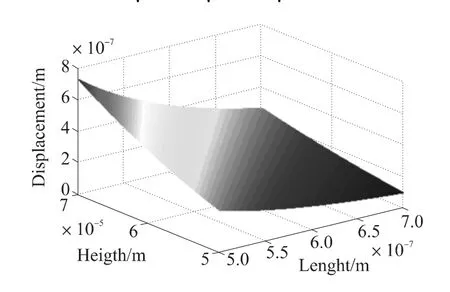
图5 悬臂梁的长、厚与挠度关系曲面

图6 (a)、(b)分别表示在a=104gn作用下悬臂梁的挠度、应力曲线

由材料属性可得Si与SiO2的许用应力分别为340 MPa、140 MPa。通过 ANSYS仿真，在104gn下SiO2悬臂梁的挠度、应力曲线如图6所示，其中最大应力为96.6 MPa，低于工程上得安全受力，且悬臂梁的最大位移为10.01 μm。通过FDTD软件在加速作用前后对跑道形微环形谐振腔进行仿真，微环谐振腔谐振波长的漂移变化量Δλ=126 pm，Q值约为103。当加速度低于1 gn时，悬臂梁的最大位移为只有几纳米，谐振腔波长的漂移较难分辨，因此该光学加速度计的测试量程为1 gn～104gn，灵敏度为1.26×10－2pm/gn。

文中对悬臂梁结构进行前4阶模态仿真，如表2所示，其二阶频率远远高于一阶频率，不会对悬臂梁的工作频率造成干扰。

表2 悬臂梁不同谐振模态下的谐振频率

在上述结构参数下，由式(1)可以得到加速度a与光场幅值A(x)的曲线关系如图7所示。

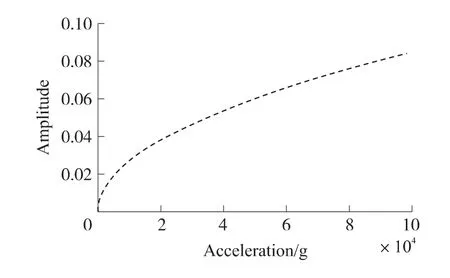
图7 加速度与光场幅度曲线图

4 结论

文中设计了一种新型高g抗冲击光学微腔加速度传感器，并针对光波导、谐振微环腔等微型光学结构及悬臂梁结构进行了优化设计和分析;通过比较不同材料的物理及光学性质，选择以Si作为光学结构材料，SiO2为悬臂梁的SOI材料，从而得到较大的抗冲击、高量程传感器。其测试量程为1 gn～104gn，灵敏度为1.26×10－2pm/gn，满足弹体侵彻以及打靶过程中的加速度的测试要求，为以后集成光学高g加速度传感器的生产加工奠定了理论基础。

致谢

作者闫树斌特别感谢山西省教育厅优秀青年学术带头人的资助，同时，本项目部分得到创新项目的资助(7130907)。

［1］ 许高斌，祖民，陈兴.SOI特种高g值MEMS加速度计设计与分析［J］.电子测量与仪器学报，2010，24(6):561－568.

［2］ 石云波，朱政强，刘晓鹏，等.高g值加速度计的设计与冲击特性分析［J］.爆炸与冲击，2010，60(3):329－332.

［3］ 唐军，赵锐，石云波，等.高冲击环境下MEMS大量程加速度传感器结构的失效分析［J］.传感技术学报，2012，25(4):483－486.

［4］ 陈凌威，宋竞，唐洁影.冲击下悬臂梁断裂可靠性的节点分析法［J］.传感技术学报，2010，3(23):367－372.

［5］ O’Reilly R，Tang H，Chen W，High-g Testing of MEMS Devices，and Why［C］//IEEE Sensors 2008 Conference.2008，148－151.

［6］ Shi Y，Zhu Z，Liu X，et al.Dynamic Property Test of a Novel Highg Microaccelerometer［C］//ASICON’09.IEEE 8th International Conference.2009，633－635.

［7］ Christiane Ziegler.Cantilever-Based Biosensors［J］.Annal Bioanal Chem，2004，379:946－959.

［8］ Vidic A，Then D，Ziegler Ch.A New Cantilever System for Gas and Liquid Sensing［J］.Ultramicroscopy，2003，97:407－416.

［9］ Yu L S，Guan Z F，Liu Q Z.Silicon on Insulator Photoelastic Optical Waveguide and Polarizer［J］.Applied Physics Letters，1995，16(66):2016－2018.

［10］ Bipin Bhola，William H Steier.A Novel Optical Microring Resonator Accelerometer［J］.IEEE Sensors Journal，2007，12(7):1759－1766.

［11］ Rokhsari H，Kippenberg T J，Carmon T，et al.Theoretical and Experimental Study of Radiation Pressure-Induced Mechanical Oscillations(Parametric Instability)in Optical Microcavities［J］.IEEE Journal of Selected Topics in Quantum Electronics，2006，1(12):96－107.

［12］ Isa Kiyat，Coskun Kocabas，Atilla Aydinli.Integrated Micro Ring Resonator Displacement Sensor for Scanning Probe Microscopies［J］.Journal of Micromechanics and Microengineering，2004，14:374－381.

［13］ Vaibhav Mathur，Jin Li，William D Goodhue.FEM Simulation of a Micro-Cantilever Optical-MEMS Sensor［C］//Proceedings of the COMSOL Μsers Conference.2006，Boston.