基于双截面ERT对鼓泡床气含率分布的可视化测量*
2012-06-10杨程屹王化祥崔自强
杨程屹,王化祥,崔自强
(天津大学电气与自动化工程学院,天津300072)
鼓泡床(鼓泡塔)是一种重要的化学反应器,被广泛应用于吸收、氧化、发酵、生化反应、废水处理等化工过程[1]。运行时,塔内充满液体,气体从底部通入,上升并分散成气泡,与液体接触发生反应,同时搅动液体增加传质速度。虽然鼓泡床具备结构简单、运行成本低等诸多优势,但气泡易产生聚并,降低效率,甚至导致事故。
为实现安全生产、提高效率,局部和整体气泡/液体流动和混合特性成为主要研究内容,气含率作为一个关键特征参数。径向和轴向气含率分布的定性和定量分析尤为必要[2],对气体分布器(多空塔板)的设计有重大指导意义。但是工业反应多数在高温、高压、非透明环境下进行,限制了许多测量技术的应用。
电阻层析成像ERT(Electrical Resistance Tomography)作为一种无损伤、无干扰及可视化检测技术,在多相流研究领域得到广泛关注[3]。与传统技术相比,ERT可提供气、液分布的实时动态图像、累计断层图像,并能通过图像灰度计算得到局部气含率、平均气含率以及径向分布等重要信息。
1 ERT系统
1.1 硬件系统构成
ERT系统通常由3个部分组成:电极阵列、数据采集系统及成像计算机,如图1所示。电极阵列形成可旋转扫描被测场域的空间敏感场,使场域内部介质电导率分布变化对敏感场产生调制作用;数据采集系统完成产生激励信号、电极状态控制、信号调制与解调等工作。基于图像重建算法重建敏感场电导率分布的二维或三维图像,提取气含率、流速等信息。
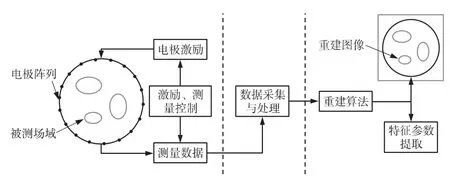
图1 ERT测量系统结构示意图
1.2 硬件技术指标
数据采集系统采用天津大学电学成像小组自主研发的ERT系统,双截面各16电极,实时采集速度可达800帧/s,成像速度可达300帧/s(直接成像算法)[4-6]。图 2 为数据采集系统框图。
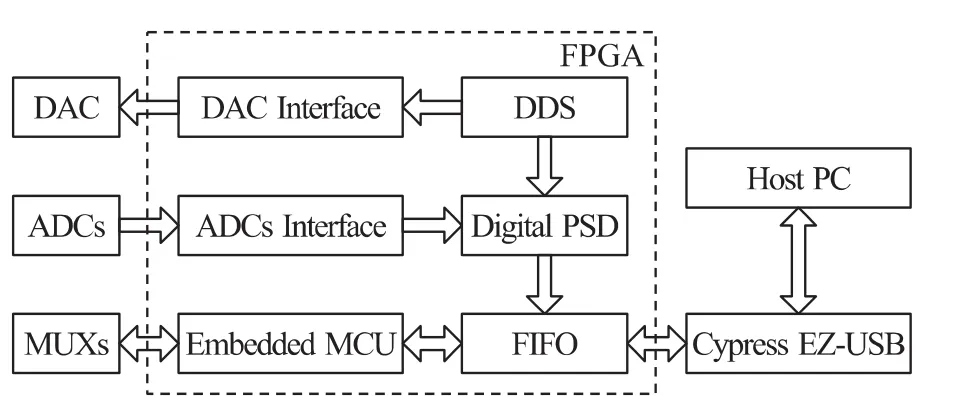
图2 数据采集系统框图
数据采集系统基于高性价比FPGA(Xilinx Spartan-3 系列),包括数模转换(DAC)、模数转换(ADC)、USB 接口以及其他前端电路[7-8]。激励信号由FPGA上的DDS IP核直接生成,经过数模转换、滤波、放大,通过扫描电极产生的测量信号经模数转换、数字相敏解调,最终通过USB接口传至上位计算机。
2 成像原理与图像重建
ERT问题可分正问题与逆问题求解。
2.1 正问题与有限元仿真
电阻层析成像系统的正问题求解,即通过有限元仿真,计算灵敏度矩阵。结合仿真软件COMSOL与MATLAB,利用COMSOL建立三维模型,如图3所示,设定微分方程及边界条件,进行仿真,并根据式(1)计算灵敏度矩阵[9]。
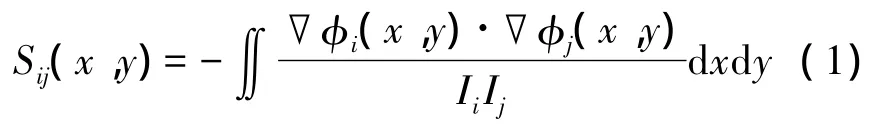
式中:φi为电极对(i,i+1)激励,其余电极悬空(高阻态)时的电势分布;φj为电极对(j,j+1)激励时的电势分布;Sij(x,y)表示电极对(i,i+1)激励,(j,j+1)测量时的灵敏度矩阵系数。
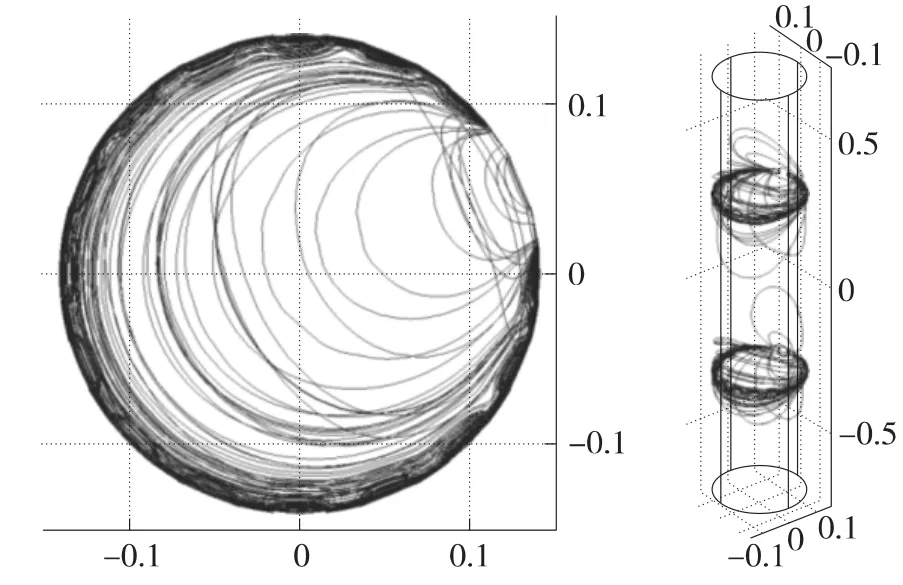
图3 有限元仿真模型
2.2 逆问题与图像重建算法
ERT逆问题求解具有病态性及不定性。通常分为直接求解法及迭代法。直接求解算法,如线性反投影(LBP),成像速度快,但获得图像边缘模糊;而迭代算法,如共轭梯度法、Newton-Raphson法、Landweber法等[10-11],可获得较高分辨率图像,但计算速度相对较慢。
本系统采用Landweber预迭代算法[12],分两步进行:首先离线进行迭代(一般100次),然后在线一步成像,在保证实时性的同时有较好的成像质量。迭代格式为
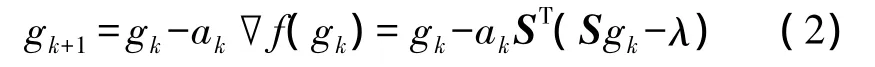
其中,g为灰度值变量,λ为测量值,S为灵敏度系数矩阵,ak是第k次迭代步长。将A0=aST(0<a<2/λmax(SST))及 gk=Akλ 代入,得到
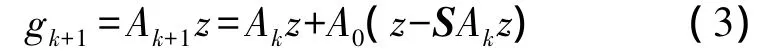
简化为
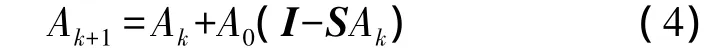
预迭代过程离线计算式(4),获得S的一个广义逆,在线根据式(5)计算图像。

2.3 由ERT重建图像计算气含率
根据麦克斯韦公式[13-15],当气含率低于 0.25时[16],可通过电导率分布计算得到气含率分布。
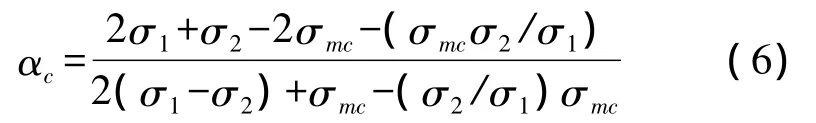
其中,σ1为液相(自来水)的电导率(约为0.1 mS/cm~1.0 mS/cm),σ2为气相的电导率,σmc是混合相的平均电导率。由于σ2≪σ1,式(6)可化简为
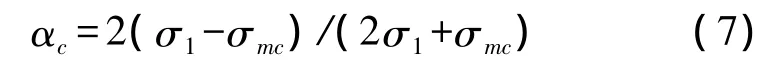
3 结果
图4为气-液鼓泡床实验装置示意图。塔内充满自来水,由底部鼓入空气,通过阀门控制进气流速,空气经过塔板1、2(多孔圆盘,水平嵌于塔内),打碎成为小气泡,形成气、液混合反应,最后由顶部排出。ERT电极(不锈钢制)设置在上层塔板2上下两侧,每层16电极,等间距分布。同时通过差压变送器及电导探针测量,以互相验证结果[17],其精度约为5%[18]。

图4 鼓泡床实验装置示意图(单位:毫米)
电导率及气含率分布图像可由成像软件直接计算并实时显示。在各不同气速下,取200帧图像计算平均值,

其中M为每幅图像像素数。
表2(见下一页)给出了不同气速条件下,ERT成像结果:电导率分布及气含率分布图像。随气速提高,中心区域电导率降低,气含率升高。
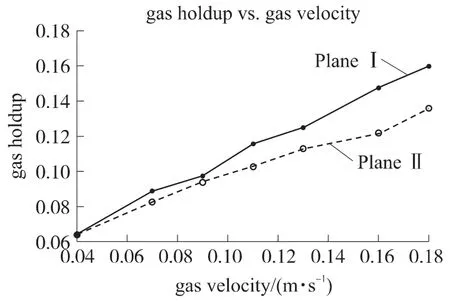
图5 ERT平均气含率随气速变化关系
气含率平均值随气速的变化关系如图5所示,与图像结果吻合,气含率随气速升高而升高,大致呈线性相关。截面1的气含率较截面2高,在高气速下,尤为明显。由于空气的溶解率较低,并非溶于水所致。而是因为空气经过塔板重新分配后,分布情况、气泡大小发生改变,大气泡破碎为小气泡。由于ERT空间分辨率相对较低(特别处于中心区域),因此大气泡图像较为清晰,小气泡及气泡群相对模糊。
不同气速下,各截面的径向气含率分布如图6所示。随气速升高,气含率升高。截面1中心(如r/R<0.1)高、边缘低;截面2,经过筛板分散气泡后,在约r/R=1/3处,气含率出现最大值,边缘较低。
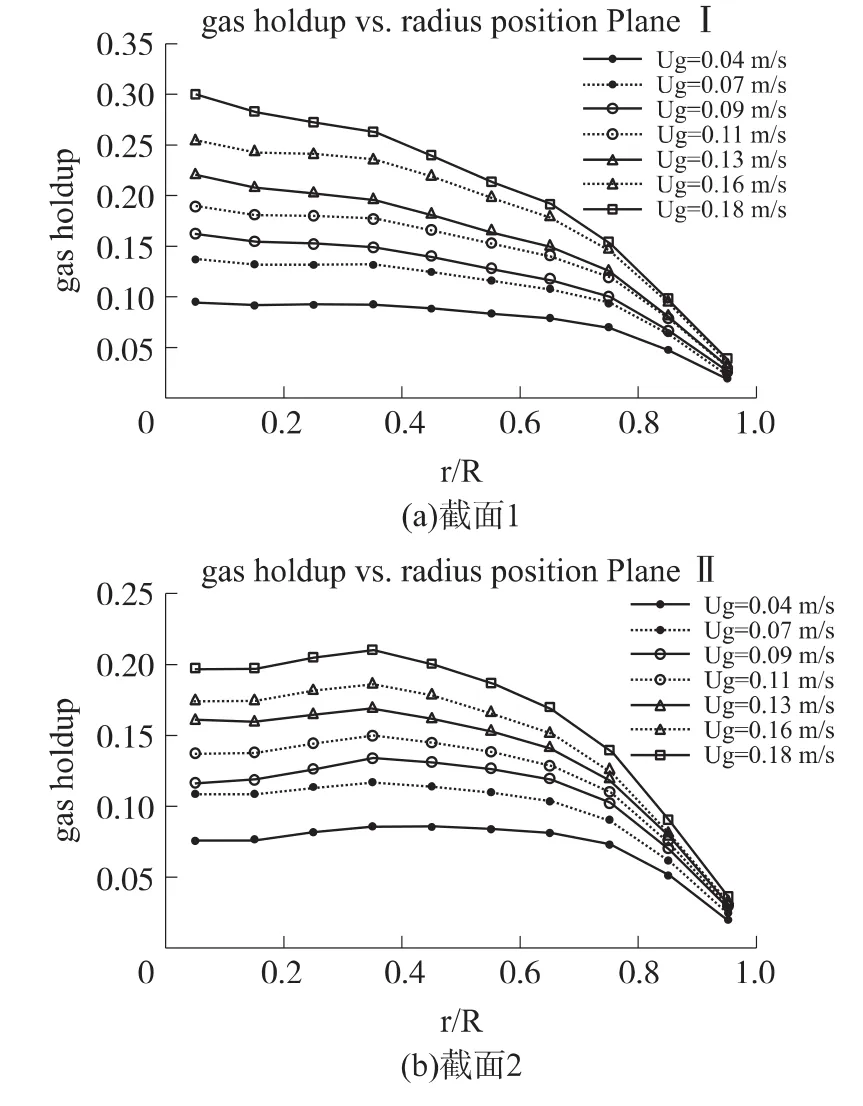
图6 ERT气含率径向分布
表1列出了不同气速下压差法所得气含率结果及ERT所得结果。由于压差法只能获得截面处气含率平均值,仅为一个数值,而ERT可获得整个截面的分布图像(表2),同时测量偏差较低,两截面分别为6.49%及5.88%。同平均气含率结果一致,在相同径向位置,截面1较截面2高。
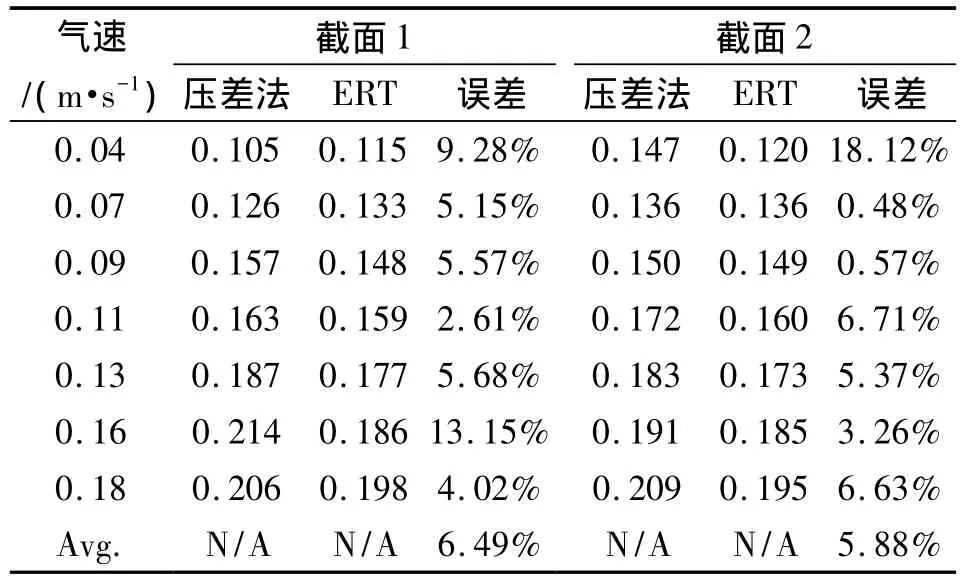
表1 压差法气含率结果与ERT结果对比

表2 电导率及气含率分布
图7为气速0.13 m/s时,ERT结果与气泡法所得径向气含率结果比较,从图中可知,误差小于等于5%。截面1的最小和最大误差分别出现在约r/R=0.65和 r/R=0.85处,截面2在边缘处误差达到最小。
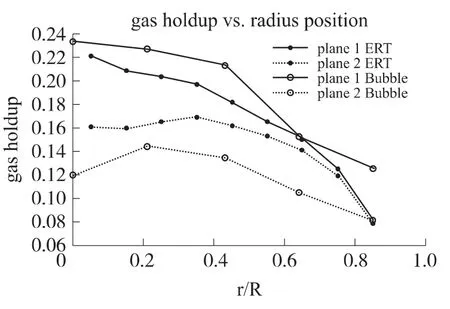
图7 气泡法气含率径向分布结果与ERT结果比较
4 结论
将ERT应用于鼓泡床测量的初步结果显示,与压差及电导探针等传统方法比较,相对误差≤5%。同时通过ERT图像及数据均观测到两测量截面气含率分布差异。为提高鼓泡床反应效率及优化设计提供了有效的可视化手段。
[1]Kazakis N A,Mouza A A,Paras Kazakis S V.Experimental Study of Bubble Formation at Metal Porous Spargers:Effect of Liquid Properties and Sparger Characteristics on the Initial Bubble Size Distribution[J].Chem Eng J,2008,137:265-281.
[2]Dudukovic M P.Opaque Multiphase Flows:Experiments and Modeling[J].Experimental Thermal and Fluid Science,2002,26:747-761.
[3]Zhang Tongwang,Jin Haibo,He Guangxiang,et al.Application of Pressure Transducing Technology to Measurement of Hydrodynamics In Bubble Column[J].Journal of Chemical Industry and Engineering(China),2004,55(3):476-480.
[4]崔自强,王化祥,许燕斌,等.双截面电阻层析成像系统设计[J].天津大学学报,2010,43(2):115-120.
[5]Ziqiang Cui,Huaxiang Wang,Lei Tang,et al.A Specific Data Acquisition Scheme for Electrical Tomography[C]//Instrumentation and Measurement Technology Conference Proceedings,2008,726-729.
[6]Yang Chengyi,Wang Huaxiang,Cui Ziqiang.Visualization Imaging Software Design for Electrical Tomography[C]//Imaging Systems and Techniques,2011,25-28.
[7]Zhang Xuehui,Wang Huaxiang,Cui Ziqiang,et al.A Novel ECT System Based on FPGA and DSP[C]//Innovative Computing,Information and Control,2007,510.
[8]张凌烽,王化祥.基于FPGA和DSP的电阻层析成像数据采集系统[J].传感技术学报,2011,24(7):1011-1016.
[9]Lehr J.A VectorDerivation Usefulin ImpedancePlethys-Mographic Field Calculations[J].IEEE Transactions on Biomedical Engineering,1972,BME-19(2):156-157.
[10]Yang W Q,Lihui Peng.Image Reconstruction Algorithms for Electrical Capacitance Tomography[J].Meas Sci Technol,14 R1,2003.
[11]马世文,王化祥.基于QR分解的对称共轭梯度法成像算法[J].传感技术学报,2011,24(8):1168-1171.
[12]Wang Huaxiang,Wang Chao,Yin Wuliang.A Pre-Iteration Method for the Inverse Problem in Electrical Impedance Tomography[J].IEEE Transactions on Instrumentation and Measurement,2004,53(4):1093-1096.
[13]Wang M,Jones T F,Williams R A.Visualization of Asymmetric Solids Distribution in Horizontal Swirling Flows Using Electrical Resistance Tomography[J].Trans IChemE,2003,81,Part A:854-861.
[14]Lucas G P,Cory J,Waterfall R C,et al.Measurement of the Solids Volume Fraction and Velocity Distributions in Solids-Liquid Flows Using Dual-Plane Electrical Resistance Tomography[J].Flow Measurement and Instrumentation,1999,10(4):249-258.
[15]George D L,Torczynski J R,Shollenberger K A,et al.Validation of Electrical-Impedance Tomography for Measurements of Material Distribution in Two-Phase Flows[J].International Journal of Multiphase Flow,2000,26(4):549-581.
[16]Sigrist L,Dossenbach O,Ibl N.On the Conductivity and Void Fraction of Gas Dispersions in Electrolyte Solutions[J].Journal of Applied Electrochemistry,1980,10(2):223-228.
[17]Krishna R,Sie S T.Design and Scale-up of the Fischer-Tropsch Bubble Column Slurry Reactor[J].Fuel Processing Technology,2000,64(1-3):73-105.
[18]Tang Chengzhi,Theodore J Heindel.Estimating Gas Holdup Via Pressure Difference Measurements in a Cocurrent Bubble Column[J].International Journal of Multiphase Flow,2006,32(7):850-863.
