一种基于小波分时灰度矩与概率神经网络的电网故障诊断方法

罗 毅，程宏波，吴 浩，李 莺

（1.四川理工学院自动化与电子信息学院，四川自贡 643000;2.华东交通大学电气工程学院，江西南昌 330013）

0 引言

电力系统是一个高可靠性要求的动态系统，任何故障的发生都有可能对整个系统的安全稳定运行产生严重威胁，甚至引起整个系统的故障灾变。为限制电力系统故障的不利影响，实时、可靠、快速的故障诊断方法对电力系统至关重要。

随着同步相量测量技术的日渐成熟和广泛应用，故障时大量暂态数据的快速获取已经成为现实，这些数据较稳态数据包含有更为丰富的故障信息。如何有效地对大量的暂态数据进行分析，快速有效地提取其中能够反映故障的特征信息，已是当前电力系统故障诊断的一个研究热点之一［1-4］。

小波变换作为一种时间－尺度的多分辨率分析方法，在非平稳信号的特征提取与分离上具有较大的优势，变换之后的小波系数中包含有比较完整的原信号的信息。灰度图是不同时间和尺度上各小波系数的直观表示，但它依赖于人的主观判断，更适应于人的定性观测。灰度矩可以定量的描述灰度图中像素点的分布情况以及灰度图的几何形状［5］，能更全面地反映信号特征，因而可利用故障后暂态信号小波变换灰度图的矩信号来作为故障判断的特征信息。

概率神经网络学习规则简单，训练速度快，具有较强的模式分类、非线性函数逼近和自适应学习能力，在电力系统中的应用也越来越多［6］。利用它的强分类能力将更有助于故障的自动识别。

本文在分析小波变换的灰度图及灰度矩的原理的基础上，给出了小波分时灰度矩的定义、计算方法及实现步骤，提出将小波分时灰度矩与概率神经网络相结合的电网故障诊断方法，以小波分时灰度矩作为概率神经网络的输入，诊断结果作为输出，实现对电网故障类型的自动识别。通过PSCAD/EMTDC对电力系统不同类型的故障进行了仿真，最终诊断结果验证了小波分时灰度矩能较好的反应电力系统的故障特征;与概率神经网络相结合，可有效地识别电网的故障类型，对电力系统的故障处理具有重要意义。

1 小波灰度图及其灰度矩

1.1 小波灰度图

小波变换克服了传统傅立叶变换的缺点，提出了变分辨率的时频分析思想，具有用多重分辨率来刻划信号局部特征的能力，适用于探测信号中的瞬态成分，因此，在故障诊断中得到了广泛的应用。

小波变换之后的小波系数中包含有比较完整的原信号信息。小波系数的分布情况可用灰度图的形式呈现出来，小波灰度图实际上是小波变换的时间－尺度－系数3者关系的二维表示。其中，横轴表示信号沿时间方向上的位置，纵轴表示尺度大小，而每个点的灰度深浅表示小波系数的幅值大小。

通过灰度图可以直观地看到某一时刻一个复杂信号由哪些频率（尺度）成分构成。不同信号对应的灰度图是不同的，特别是发生故障时的故障信号与正常时信号的灰度图差异更为明显，因此可以通过灰度图对故障进行识别。但直接根据灰度图对故障进行识别，受诊断主体的主观影响较大，同时还存在很大的模糊性，很难得到客观准确的结论，不利于计算机的自动诊断。本文引入图像识别领域中的矩特征来描述灰度图中象素点的整体分布情况，以及灰度图像的基本几何形状，得到灰度矩作为故障分析的征兆量。

1.2 小波分时灰度矩

在图像识别领域，矩特征是应用很广泛的一种图像统计参数，它描述了一幅灰度图中所有像素点的整体分布情况，以及灰度图像的基本几何形状。

灰度矩的定义为［7］

（1）式中:cij是信号经小波变换后的系数矩阵［C］m×n的元素;m和n分别对应小波变换的尺度和时间;表征元素与元素c11之间的距离，相当于灰度图中某一个像素点（i，j）与参考点（1，1）之间的几何长度。灰度矩gk反映了灰度图中像素灰度的分布情况，可用来作为反映电力系统故障的故障特征。由于系数矩阵元素较多，k越大，乘方运算的时间开销越多，文献［7］的研究表明，k=1的一阶灰度矩一样具有较高的区分能力，为减小计算开销，提高故障诊断的实时性，本文选取一阶灰度矩作为故障特征。

为了描述信号随时间的变化，定义分时灰度矩来描述小波系数在时间上的变化情况。分时灰度矩对小波变换的灰度图进行时间上的划分，以分别求得不同时刻的灰度矩的值，从而得到小波系数随时间的变化情况。具体来说就是将变换后的小波系数矩阵［C］m×n沿时间划分为l等份，然后分别对每一个分时矩阵求灰度矩，最后得到一个可以反映信号随时间变化的灰度矩序列G=［g（1），g（2），…，g（l）］。其中

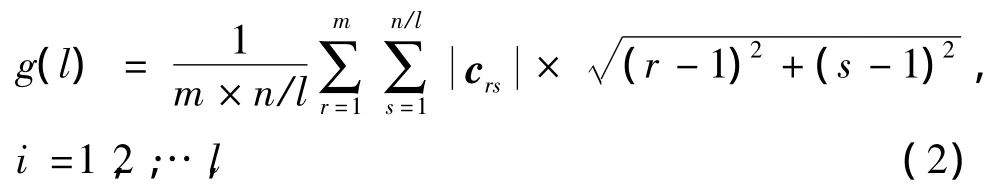
（2）式中，crs是小波系数矩阵［C］m×n依时间划分的一个m×n/l阶子矩阵。

基于连续小波变换信号提取一阶分时灰度矩征兆的基本步骤如下。

1）设待分析信号为{an}，进行归一化处理得到序列{xn}，其中

2）选择合适的小波和分解尺度对{xn}进行连续小波分解，得到m×n阶系数矩阵［Cij］;

3）将系数矩阵［C］m×n沿时间划分为l等份，得到l个m×n/l阶子矩阵crs。

4）分别对每一个分时子矩阵crs按式（2）计算其灰度矩，得到灰度矩序列。

2 概率神经网络模型

概率神经网络（probability neural network，PNN）是一种前向型网络，由径向基层和竞争层组成，其结构如图1所示。

图1 概率神经网络结构Fig.1 Structure of probability neural network

概率神经网络的实质是一个分类器，根据概率密度函数的无参估计进行贝叶斯决策而得到分类结果。当训练样本数据足够多时，概率神经网络收敛于一个贝叶斯分类器，可用来解决分类问题［8］。

该网络的输入层神经元个数与训练样本向量的个数相同，输出层神经元个数等于训练样本数据的种类个数;而且输出层是竞争层，每个神经元分别对应一个数据类型。得出概率密度函数最大的那个神经元输出为1，为待识别的样本模式类别，其他神经元输出则为0。PNN作为径向基网络的一种，适合于模式分类，故可采用小波灰度矩作为特征量，以概率神经网络作为分类器，来对电网不同类型的故障进行识别和判断。

3 基于小波分时灰度矩的电力系统故障识别

3.1 小波分时灰度矩的获取

通过以上分析可知，电力系统故障信号与正常信号的灰度图存在较大差异，而灰度矩则能将这种差异定量反映出来。小波分时灰度矩将灰度矩与时间联系起来，能更准确反映电力系统故障信号随时间变化的关系，可用于电力系统的故障诊断。

本文以电力系统中输电线路发生短路故障为例，以各相电流为研究对象，通过小波变换得到各相电流小波变换的灰度图及对应的分时灰度矩，以分时灰度矩作为故障特征，实现对电网故障的识别和判断。

采用PSCAD/EMTDC对图2所示的输电线短路进行了仿真，系统的模型参数:变压器容量100 MVA，线路接有100 MW负载，在距离左侧母线180 km处发生短路故障，线路总长260 km，线路参数［9］R1=0.070 5 Ω/km，L1=1.274 mH/km，C1=0.086 μF/km;R0=0.323 Ω/km，L0=3.822 mH/km，C0=0.006 05μF/km。

图2 简化的故障模型示意图Fig.2 Simplified model with fault

发生AB两相短路时各相电流的波形及其小波变换的灰度图如图3所示。

从图3中可以看到，发生故障的相电流变换的小波灰度图与正常相电流的小波灰度图有着较大的区别。特别是在故障发生时刻，灰度图的区别更加明显。

利用db4小波对电流信号进行变换，并取每0.01 S计算一次，即l=50，按前述方法计算出的AB相短路时各相电流小波分时灰度矩如图4所示，采用dmey和meyer小波母函数计算得到的灰度矩与其区别不大。从图4中可以看出，小波灰度矩在故障发生时刻显著增加，因此可作为特征量判断故障的发生。

表1所示为图2系统在不同运行情况下各相电流小波变换后分时灰度矩的值。从表1中可以看出，故障相电流小波分时灰度矩的值Gfault≥0.160 7（B相接地短路时电流Ib的分时灰度矩），正常相电流小波分时灰度矩的值Gnornal≤0.049 7（A相接地短路时电流Ib的分时灰度矩），两者之间有较大差距。

接地故障与非接地故障中性点电流灰度矩的值相差也非常明显（接地故障时≥0.091 9，非接地故障时≤7.395 2e-004），表明采用小波灰度矩作为反映故障的特征量是合适的。为了更加直观地表示故障相与正常相小波分时灰度矩值的差异，将4种典型情况的电流灰度矩值列于图5中。

图3 发生两相（AB）短路时，电流波形图及对应的小波变换灰度图Fig.3 Currentwaveform and its wavelet gray picture when phase A direct to phase B

图4 发生两相（AB）短路故障时，各相电流小波变换后的分时灰度矩Fig.4 Time divided graymoment of currents when phase A direct to phase B

表1 不同情况下各相电流小波变换后分时灰度矩的值Tab.1 Time divided graymoments of currents under different circumstances

通过对表1中数据及图5中图形的分析，可以看到，利用小波分时灰度矩作为反映故障的特征量，具有较好的区分能力。

图5 4种典型情况下电流小波分时灰度矩对比图Fig.5 Different graymoments under differents types of faults

3.2 基于概率神经网络的故障识别与判断

PNN网络可直接由Matlab提供的函数net=newpnn（P，T，S）来创建，其中:P为输入向量，T为目标向量，S为扩展参数（默认为0.1）。建立一个2层PNN网络，第1层为径向基层，激励函数为径向基函数radbas，权值向量设置为输入向量的转置P';第2层为竞争层，其激励函数是compet，权值向量为目标向量T。以各相电流的小波灰度矩作为PNN网络的输入，11种模式的分类结果作为输出。

分别改变故障位置、线路负荷、过渡电阻的大小，对图1所示系统的11种情况各进行130次仿真，得到130组共1 430个数据样本。对每种情况各随机选取100组共1 100个数据作为训练样本，另外30组作为测试样本，其识别结果如表2所示。

表2 概率神经网络测试结果Tab.2 Test result of PNN

从表2测试结果可以看出。

1）以小波分时灰度矩作为故障特征，能较好地区分电网故障与正常运行的情况，对电网正常运行的正确识别率达100%;

2）对单相故障及三相故障的识别能力强，三相故障和部分单相故障的正确识别率达100%。说明在采用小波灰度矩作为故障特征时，单相故障及三相故障的特征表现明显，因而识别结果较好。这也与测试和训练的样本数有限有关，由于仿真得到的测试样本较真实情况更为理想，故而仿真实验中得到的正确率可能会比实际应用中的要高;

3）对两相短路故障及两相接地短路故障的识别能力较其他故障类型要差，主要是两相短路和两相接地短路时，小波灰度矩的表现有较大相似性。当接入的过渡电阻较大时，他们之间的差异进一步减小，从而给识别造成了一定的困难;

4）一阶灰度矩对电网故障具有较高区分度。通过对2阶灰度矩的验证，在消耗3倍于一阶运算时间的情况下，大部分故障的识别率与一阶基本相同，没有明显改善。

故障仿真结果表明，采用小波分时灰度矩的方法具有较好的故障识别能力，结合概率神经网络，能够较好的对电力系统的短路故障进行诊断。

4 结论

故障信号经小波变换后的系数中包含有丰富完整的故障信息，灰度图能将这些信息直观的表示出来，灰度矩则能将这些信息加以量化，更具体地反映信号特征;分时灰度矩将灰度图中蕴含的故障特征信息沿时间作了细化处理，可以定量展现故障的特征信息，因而能更准确地反映故障信号特征，是进行输电网故障识别的一种有效手段;概率神经网络学习规则简单，分类能力强，将小波灰度矩与概率神经网络相结合，可有效地实现对输电网故障的自动识别和诊断。

［1］王钢，李志铿，李海锋.±800kV特高压直流线路暂态保护［J］.电力系统自动化，2007，31（21）:40-43.

WANG Gang， LI Zhi-keng， LI Hai-feng. Transient based protection for±800 kV UHVDC transmission lines［J］.Automation of electric power system，，2007，31（21）:40-43.

［2］符玲，何正友，麦瑞坤，等.近似熵算法在电力系统故障信号分析中的应用［J］.中国电机工程学报，2008，28（28）:68-73.

FU Ling，HE Zheng-you，MAIRui-kun，et al.Application of approximate entropy to faultsignalanalysis in electric power system［J］.Proceedings of the CSEE.2008，28（28）:68-73.

［3］ 韩志伟，刘志刚，鲁晓帆，等.基于CUDA的高速并行小波算法及其在电力系统谐波分析中的应用［J］.电力自动化设备，2010，30（1）:98-101.

HAN Zhi-wei，LIU Zhi-gang，LU Xiao-fan，et al.Highspeed parallel wavelet algorithm based on CUDA and its application in power system harmonic analysis［J］.Electric Power Automation Equipment.2010，30（1）:98-101.

［4］朱锋峰，任震，黄雯莹.基于小波变换修正幅值的电力系统频率偏移诊断方法［J］.电网技术，2004，28（11）:34-37.

ZHU Feng-feng，REN Zhen，HUANG Wen-ying.A method to diagnosis frequency shift of power systems based on modified amplitude of wavelet transform.Power system technology，2004，28（11）:34-37.

［5］ 陈喜阳，王善永，孙建平，等.基于CWT灰度矩的水电机组振动征兆提取［J］.电力系统自动化，2007，31（9）:68-71.

CHEN Xi-yang，WANG Shan-yong，SUN Jian-ping，et al.Extraction of vibration symptom for the hydro-power unit based on CWT graymoment［J］.Automation of electric power system，2007，31（9）:68-71.

［6］孙晓刚，张建华，侯国莲，等.基于概率神经网络的凝汽器故障诊断研究［J］. 现代电力，2005，22（3）:58-61.

SUN Xiao-gang，ZHANG Jian-hua，HOU Guo-lian，et al.Condenser fault diagnosis using probabilistic neural networks［J］.Modern ElectricPower，2005，22（3）:58-61.

［7］杨涛.基于小波分时尺度矩特征的多状态信息融合振动故障诊断和预测方法研究［D］.武汉:华中科技大学，2009.

YANG Tao.Vibration fault diagnostics and prognositics ofmulti-state information fusion based on wavelet time-division scale level moment［D］.Wuhan:HuaZhong University of Seience and Teelinology，2009.

［8］贾勇，何正友，赵静.基于小波熵和概率神经网络的配电网电压暂降源识别方法［J］.电网技术，2009，33（16）:63-69.

JIA Yong，HE Zheng-you，ZHAO Jing.A Method to Identify Voltage Sag Sources in Distribution Network Based on Wavelet Entropy and Probability Neural Network［J］.Power System Technology，2009，33（16）:63-69.

［9］沈晓凡，粟小华，周春霞.750kV输电线路对继电保护的影响［J］.电力设备，2006，7（1）:18-19.

SHEN Xiao-fan，SU Xiao-hua，ZHOU Chun-xia.Influence of 750kV transmission line on protection［J］.Electrical Equipment，2006，7（1）:18-19.