非线性价格的认知中继网络功率控制方法研究
2012-06-06杨克利刘彰茂
蒋 青,杨克利,刘彰茂
(重庆邮电大学移动通信技术重点实验室,重庆 400065)
0 引言
认知中继网络作为一种认知无线电系统,它不仅能提高频谱利用率,缓解目前频谱资源紧张的问题[1-2],而且可以增大网络覆盖范围从而提高系统容量,由此大量学者进行了深入的研究。
Simon.Haykin提出可以采用信息论和博弈论的方法对认知无线电功率控制进行分析[3]。Goodman研究团队研究了线性代价的非合作功率控制博弈模型[4-5],为了提高蜂窝网络公平性,文献[6]提出了与信道增益成正比的链路增益代价函数。文献[7]用博弈论方法研究了进行数据通信的认知中继网络功率控制问题。在现有的研究基础上,本文主要研究解决应用于语音通信的中继网络功率控制问题。结合认知中继网络的通信特点,提出一种非线性成本函数,该功率控制方法减少了系统总的功率消耗,大大改善了网络通信性能。
1 系统模型及效用函数
1.1 系统模型
在认知无线电环境中协作通信系统的3节点模型,如果目的节点D无法接收到源节点S的信息,那么此时的3节点模型[8]就是认知中继网络模型。如图1所示,主用户发射机U1向主用户接收机U2发送信息,从用户包括源节点S、认知中继节点R、目的节点D,源节点S和认知中继节点R以半双工方式工作,协作中继方式为 DF(decode and forward)模式[8-9]。
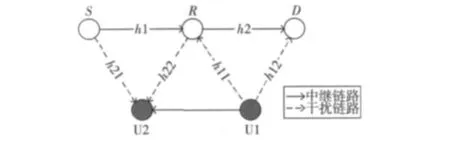
图1 认知中继网络功率控制模型Fig.1 Power controlmodel of cognitive relay network
从用户以衬垫方式与主用户共享授权用户的频谱。图1模型不采用前向纠错编码技术,第1阶段和第2阶段的通信调制方式可以任选,这里都采用非相关 FSK(frequency-shift keying)。
1.2 效用函数及成本
在认知中继网络传送语音信号时,能够容忍一定的传输出错,不重传传输出错的信息。假设中继通信发送的信息包长度为Lbit,信道编码后信息包的长度为Mbit(M>L),信息发送的速率为Rcbit/s,中继通信第1阶段和第2阶段信息传输的信干比分别是γ1,γ2,g(γ1)是第1阶段的比特信息正确传送概率,g(γ2)是第2阶段的比特信息正确传送概率,函数g(γ1),g(γ2)的值取决于数据传输的具体情况,则第j(j∈ {1,2})阶段的吞吐量为但是当第-j阶段(不是第j阶段的另一个阶段)的信息正确传送概率很低时,即使第j阶段的信息正确传送概率趋向于1,整个认知中继通信的系统吞吐量也是很低的。所以,在定义局中人j(这里局中人1指源节点S发射机,局中人2指中继节点R发射机)效用的时候必须也要考虑第-j阶段的信息正确传送概率,如果仅考虑第j阶段的信息正确传送概率是没有意义的。在这里,提出第-j阶段通信对第j阶段通信的吞吐量影响系数η,令η=g(γ-j),0≤η≤1。因此,第j阶段通信的效用定义为

根据(1)式可以知道效用函数的物理含义是第j阶段通信的有效吞吐量。第j阶段通信的效用等于第j阶段通信的吞吐量乘以第-j阶段的信息正确传送概率g(γ-j)。也就是说,局中人j的效用不但与局中人j的发射功率pj有关,也与局中人-j的发射功率p-j有关。当调制方式为非相关FSK时g(γj)=1-BERj,BERj为第j阶段数据传输的比特信息出错率,非相干FSK的BERj表达式为
ChiWan Sung等[10]学者研究了在 CDMA 数据网络中的非合作功率控制博弈。从他们的研究知道由(1)式构成的功率控制博弈得出的纳什均衡虽是帕累托最优,但是低效的,所以必须引入成本函数以提高网络的性能。接下来研究认知中继网络的特点,提出一种与其特点相吻合的成本函数。
设第j阶段的信干比为

(2)式中:hj,h1j为各个信道增益;pU1为主用户发射机U1的发射功率;W为带宽;N0为噪声功率谱密度。

(3)式中,参数aj体现第j阶段通信的信道质量,当第j阶段通信的信道质量较好时,aj值较大。
假设认知中继通信第1阶段和第2阶段信干比分别是γ1,γ2时的系统比特信息正确传送概率等价于一条信干比为γeq的直传通信的比特信息正确传送概率,即

当g(γeq)取某一个定值时,也就是说g(γ1)g(γ2)为一个常数,假设a1<a2,存在信干比γA和 γB,且 γA>γB,满足

现在我们来分析一下是令γA=γ1,γB=γ2还是 γA=γ2,γB=γ1在满足g(γeq)=g(γA)g(γB)时认知中继网络消耗的功率较小。

当 γA=γ1,γB=γ2时,中继网络发射的功率和为

当γA=γ2,γB=γ1时,中继网络发射的功率和为

(4)式和(5)式相减,得

所以令γA=γ2,γB=γ1时使网络达到同样的传输性能时系统总消耗能量较小,使整个网络更有效率,这也就是说,当a1≤a2时控制功率使γ1≤γ2。
由上面的分析我们提出第j阶段通信发射功率需支付的价格为λ,λ为常数:那么第j阶段通信发射功率需支付的成本为

第-j阶段的通信也会影响第j阶段通信的支付价格λ,支付价格λ也应乘以影响系数η,得到有效价格g(γ-j)λ,第j阶段通信的有效支付成本为

第j阶段通信的有效价格随第-j阶段的通信信干比变化而变化,价格的非线性是本文功率控制模型的主要特点之一。
根据(1)式和(8)式,引入支付成本机制后的新效用函数为

2 非合作功率控制博弈模型
第1阶段和第2阶段通信以先后发送次序发送信息。用博弈论的术语来说,一般在时间上即使有行动的先后,而直到博弈结束时局中人相互之间都不知道其他局中人在采取何种具体策略,效果上等价于局中人在同时行动,仍称该博弈为静态博弈[11]。因此本文研究的认知中继功率控制问题是静态博弈[7]。
认知中继网络功率控制博弈的3个要素如下:
1)局中人。局中人的集合N={1,2},1表示第1阶段通信的发射机(即源节点S发射机);2表示第2阶段通信的发射机(即认知中继节点R发射机),为方便叙述,直接称为局中人1、局中人2;也称局中人j或-j(j∈N)。
2)策略。策略是发射机的功率,局中人j的策略pj∈Pj,Pj是局中人j的策略空间,

3)效用函数。由(9)式得局中人j发射功率所获得的效用为

每个局中人都以分布式的方式最大化其自身的效用。这个博弈可表示为

3 纳什均衡解探讨
根据超模博弈的条件,欲证明 (12)式博弈存在纳什均衡并且唯一,需要满足2个条件[12]:
1)策略空间Pj是紧集合;
2)收益函数满足

证明:显然,第一个条件是满足的。那么只需证明收益函数vj(pj,p-j)满足条件2)。

只要发射功率pj满足(14)式,博弈就存在唯一的纳什均衡解。

由(14)式可以知道,均衡功率是由信道参数和价格系数λ确定。


纳什均衡解满足功控的目标。
注意到局中人j在[0,p*j]内的效用vj(pj,p-j)是单调增的。考虑到局中人j最大允许的发射功率,局中人j的最佳响应策略为

所以,纳什均衡解实际值是 (p'j,p'-j)。
4 其他2种非线性价格的功率控制
下面将研究其他两种非线性价格的功率控制模型,并将它与上节中研究的非线性价格功率控制结果进行比较。
4.1 第2种非线性价格
根据第1小节的分析,提出第2种第j阶段通信发射功率支付价格ajλ,也就是说价格与信道质量参数aj成正比。所以第j阶段通信要支付的有效成本函数是

受此成本函数约束下的效用函数为

由此效用函数构成的功率控制博弈表示为

如同第3节的探讨纳什均衡解,可以得到(18)式功率控制博弈的纳什均衡解为

由(19)式得

同样地,局中人j在[0,p*j]内的效用v'j(pj,p-j)是单调增的。考虑到局中人j最大允许的发射功率,局中人j的最佳响应策略为

所以,纳什均衡解实际值是 (p'j,p'-j)。
4.2 第3种非线性价格
为了更深入分析比较不同价格的认知中继网络功率控制的性能,在(7)式基础上进一步再提出一种非线性价格,以这个价格组成有效成本函数为

受此成本函数约束下的新效用函数为

由新效用函数构建的非线性价格功率控制博弈表示为

如同第3节的纳什均衡探讨,可以得到(23)式功率控制博弈的纳什均衡解为


由(24)式得同样地,局中人j在[0]内的效用v″j(pj,p-j)是单调增的。考虑到局中人j最大允许的发射功率,局中人j的最佳响应策略为

所以,纳什均衡解实际值是 (p″j,p″-j)。
5 全局性能分析
认知中继系统效用即认知中继系统吞吐量为

信干比γ-j,γj的值由纳什均衡解实际值(p'j,p'-j)确定。

表1 3种有效支付价格的博弈结果比较Tab.1 Comparison of results with three kinds of price
6 仿真结果
在一个CDMA系统中,各局中人位置不变,源节点S、认知中继节点R、目的节点D到主用户发射机U1和接收机U2的距离都是1 km,源节点S和认知中继节点R之间的距离是40 m,认知中继节点R和目的节点之间的距离是30 m。定帧长,无前向纠错,系统详细参数如表2所示。这里,路径增益采用一个简单的广播模型,它是无线电发射机和接收机之间距离d的函数,即


表2 仿真参数Tab.2 Simulation parameters
由上述参数可以得到a1=7.578 0,a2=23.950 2 ,则a1<a2。
由(13)式知道价格系数λ须满足

据此选择合适的λ值来对网络进行性能分析。
图2给出了价格为λ时,均衡功率与λ的关系。如图2所示,第j阶段的均衡功率pj随价格系数λ增大而减少,表明支付价格能有效地约束和控制各阶段发射机发射的功率值。同时,两个阶段发射功率值之和pj+p-j也随价格系数λ增大而减少。说明认知中继网络可以根据发送信息对性能的要求,选择合适的λ值,这可以减少整个网络的能量消耗。
图3给出了两个均衡信干比与价格λ之间的关系。图3表明功率控制达到了所要求的功率控制目标,即当a2≤a1时 γ2≥ γ1。
在获得相同认知中继系统效用情况下,3种有效支付价格功率控制的两阶段发射功率值和的比较如图4所示。从图4知道有效支付价格分别为g(γ-j)λ功率控制的功率值之和最小,有效支付价格分别为功率控制的功率值之和最大。

图5是在达到相同认知中继系统效用情况下,3种有效支付价格功率控制的主用户通信误码率比较,从图5中知道支付价格为g(γ-j)λ功率控制的主用户通信误码率最低,支付价格为功率控制的主用户通信误码率最高;此外,从图5的纵坐标看出,虽然3种有效支付价格功率控制的主用户通信误码率差别很小,这是因为在本文的仿真参数条件下从用户对主用户的干扰较小,从用户可以较安全地使用主用户的授权频段。

图5 3种有效支付价格功率控制的主用户通信误码率比较Fig.5 Comparison of Primary Communication's BER in Power Control with Three Kinds of Price
7 结论
在传输语音数据信号的认知中继网络中,研究以追求吞吐量为目标的认知中继网络的特点,提出一种非线性价格的成本函数,建立功率控制博弈模型。通过分析其纳什均衡,以纳什均衡解作为各局中人的策略,满足功率控制目标且容易实现。本文对用于语音通信认知中继网络的功率控制问题做了一些初步的研究,在下一步的工作中将更深入地研究非线性价格优化问题,以进一步提升网络的性能。
[1] MITOLA J,MAGUIRE G.Cognitive radio:Making software radiosmore personal[J].IEEE Personal Communications,1999,6(3):13-18.
[2]MITOLA J.Cognitive radio:An integrated agent architecture for software defined radio,Docter of Technology[D].Stockholm,Sweden:Royal Institute of Technology,2000.
[3]HAYKIN S.Cognitive radio:Brain-empowered wireless communications[J].IEEE Journal on Selected Areas in Communications,2005,23(2):201-220.
[4] GOODMAN D,MANDAYAM N.Power control for wireless data[J].IEEE Personal Communications,2000,7(2):48-54.
[5] SARAYDAR C,MANDAYAM N,GOODMAN D.Efficient power control via pricing in wireless data networks[J].IEEE Transactions on Communications,2002,50(2):291-303.
[6]钟卫,徐友云,蔡跃明.非合作功率控制博弈优化设计[J].解放军理工大学学报:自然科学版,2005(2):108-113.
ZHONGWei,XU You-yun,CAI Yue-ming.Effective of non-cooperative power control game[J].Journal of PLA U-niversity of Science:Natural Science,2005(2):108-113.
[7]蒋青,杨克利,唐伦.基于博弈论的最优认知中继网络功率控制[J].重庆邮电大学学报:自然科学版,2011,23(2):150-154.
JIANG Qing,YANG Ke-li,TANG Lun.Optimal power control for cognitive relay networks based on game theory[J].Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition,2011,23(2):150-154.
[8] LANEMAN JN,WORNELLGW.Distributed space-time coded protocols for exploiting cooperative diversity in wireless networks[J].IEEE Transactions Information Theory,2003,49(10):2415-2425.
[9] LANEMAN JN,TSED N C,WORNELLGW.Cooperative diversity in wirless networks:efficient protocols and outage behavior[J].IEEE Transactions on Information Theory,2004,50(12):3062-3080.
[10] CHIWan Sung,WING Shing Wong.A noncooperative power control game for multirate CDMA data networks[J].Wireless Communications, IEEE Transactions,2003,2(1):186-194.
[11]施锡铨.博弈论[M].上海:上海财经大学出版社,
2001.
SHIXi-quan.Game Theory[M].Shanghai:Shanghai Finance University Press,2001.
[12] FUDENBERG D,TIROLE J.Game Theory[M].Cambridge:MIT Press,1991:490.
