认知无线电中基于潜在博弈的信道分配算法

胡 庆，赵力力，，李 云

（1.重庆邮电大学通信与信息工程学院，重庆400065;2.重庆邮电大学无线网络实验室，重庆 400065）

0 引言

随着各种新的无线应用和无线设备的出现，通信系统对无线频谱的需求在不断增加，导致频谱资源日渐紧缺，这就促使无线频谱管理机构需要重新思考相应的管理策略。传统的固定频谱分配方法虽然使得频谱管理简单，但频谱资源利用率却非常低。认知无线电［1-2］（cognitive radio，CR）作为一种革命性频谱共享技术，可显著提高频谱利用率，解决频谱资源稀缺的问题。

博弈论是研究决策主体的行为发生直接相互作用时候的决策以及这种决策的均衡问题的理论，将它引入认知无线电系统中，可以分析和解决认知无线电中各用户竞争频谱的分布式行为问题。目前，认知无线电网络中基于博弈论的资源分配算法研究已有很多。文献［3］基于非合作博弈提出了一种分布式自适应功率控制算法，该算法能使每个用户实现周期性的信息交互和自适应地调整传输功率;文献［4］提出了一种基于超模博弈的频谱分配算法，该算法通过引入适当的价格函数来评估认知用户对主用户的影响;Niyato等［5-6］提出了一种基于代价的频谱分配算法，该算法中主用户（primary user，PU）按照一定的价格将频谱出租给次用户（secondary user，SU）使用;Wu等在文献［7］中提出了一种防欺诈重复开放共享博弈算法，该算法针对网络中次用户为接入更多的频谱而交换虚假信息，用一种基于惩罚的重复博弈来促使次用户的合作;Nie等［8］提出了一种自适应信道分配算法，该算法分别针对自私用户和合作用户定义了2个不同的目标函数;随后，Nie［9］又在文献［8］的基础上提出了联合功率控制的信道分配算法。

文献［8］提出的算法没有考虑到对网络中主用户的影响，分配结果会使主用户获得较差的信干噪比，即会影响主用户的通信质量。本文在文献［8］提出的自适应信道分配算法的基础上进行拓展研究，提出了一种改进的基于潜在博弈的分布式信道分配算法，算法以最小化系统干扰水平为目标，所构建的效用函数考虑了对主用户的干扰情况。

1 系统模型

认知无线电网络中有N个次用户的发射－接收对，M个主用户的发射－接收对，主用户与次用户随机分布在一个d×d的区域内，如图1所示。图1中PU表示主用户，SU表示次用户。每个主用户都拥有一个授权频段（即一个信道），次用户的位置在频谱分配算法执行期间是固定的或者是缓慢移动的（慢于算法的收敛时间）。次用户以分布式的方式从网络信道集合中选择信道。本文假设次用户物理层可以通过调整自己的调制方式和信道编码速率来改变数据发送速率和相应的信干噪比门限值，即如果信道分配结果不能满足主用户和次用户的QoS要求，次用户可以通过调节自身物理层的参数来满足主用户和次用户的QoS要求。假设网络中存在一条公共控制信道用于交换控制信息。

图1 频谱共享模型Fig.1 Model of spectrum sharing

次用户i发送端到次用户j接受端的信道增益用表示，次用户i发送端到主用户m接收端的信道增益用表示，主用户m发送端到其接收端的信道增益用表示，主用户m发送端到次用户i接收端的信道增益用表示。本文中信道增益的计算公式为Gij=10/d2ij，dij为发送端i到接收端j的距离，即信道增益与距离的平方成反比，这符合无线信道的基本特征。次用户i在其接收端处的SINR为

主用户m在其接收端处的SINR为

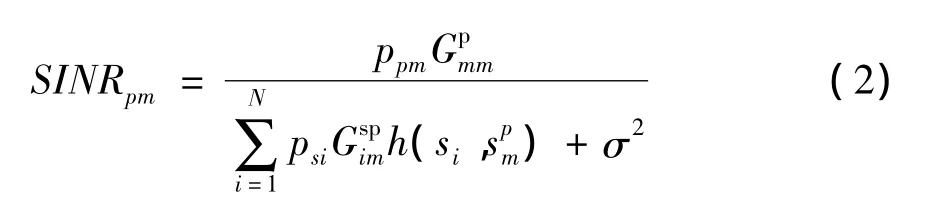
（2）式中:psi为次用户i（i∈［1，N］）的发射功率;ppm为主用户m（m∈［1，M］）的发射功率;σ2为接收端处的加性高斯白噪声功率;h为干扰函数，其定义如下

（3）式中，si与sj是次用户i与次用户j的信道选择策略，其具体意义见第2节。

2 潜在博弈分析

2.1 博弈论的数学描述

近年来，博弈论被广泛应用于认知无线电网络的资源分配中。认知无线电中频谱分配问题的博弈论数学描述的一般形式为

2.2 纳什均衡

作为博弈论的一个基本概念，纳什均衡提供了对一个博弈输出结果的预测。当博弈者的一组策略s=（si，s－i）满足（5）式时，则s就是一个纳什均衡。

也就是说，在参与者集合里，如果没有一个参与者能够靠自身策略的改变来提高自身收益时，整个参与者集合对应的策略组合就称为纳什均衡。

潜在博弈作为博弈论中的一种特殊博弈，总会收敛于一个纳什均衡［10］。如果一个博弈存在一个潜在函数能满足（6）式，则这个博弈就是一个潜在博弈。

2.3 效用函数

文献［8］中的效用函数仅考虑了网络中次用户间的相互干扰，其效用函数为

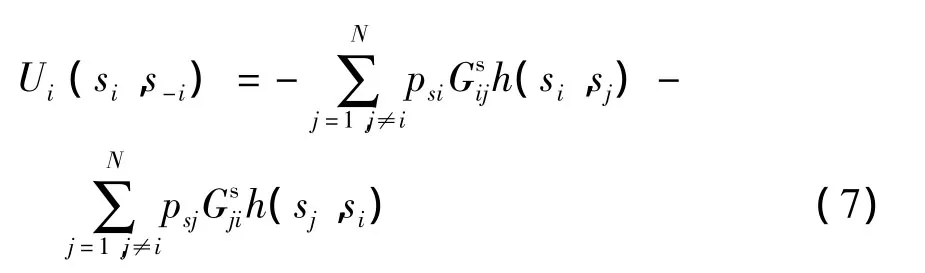
本文考虑了网络中主用户的存在，以最小化系统干扰水平为目标，所以效用函数的设计必须考虑对主用户的干扰。本文提出的效用函数为

可以看出，效用函数中不仅包含了次用户i对其他次用户和主用户的干扰，而且包括了主用户和其他次用户对次用户i的干扰，即若认知用户使用某个信道会对某个主用户产生严重干扰，那么该次用户就不会使用该信道作为通信信道。

2.4 潜在函数

对于本文提出的效用函数，我们构建其相应的潜在函数为

下面证明此潜在函数满足（6）式。

P1（si，s－i）的证明过程参考文献［9］，这里不再证明，只给出其结果为

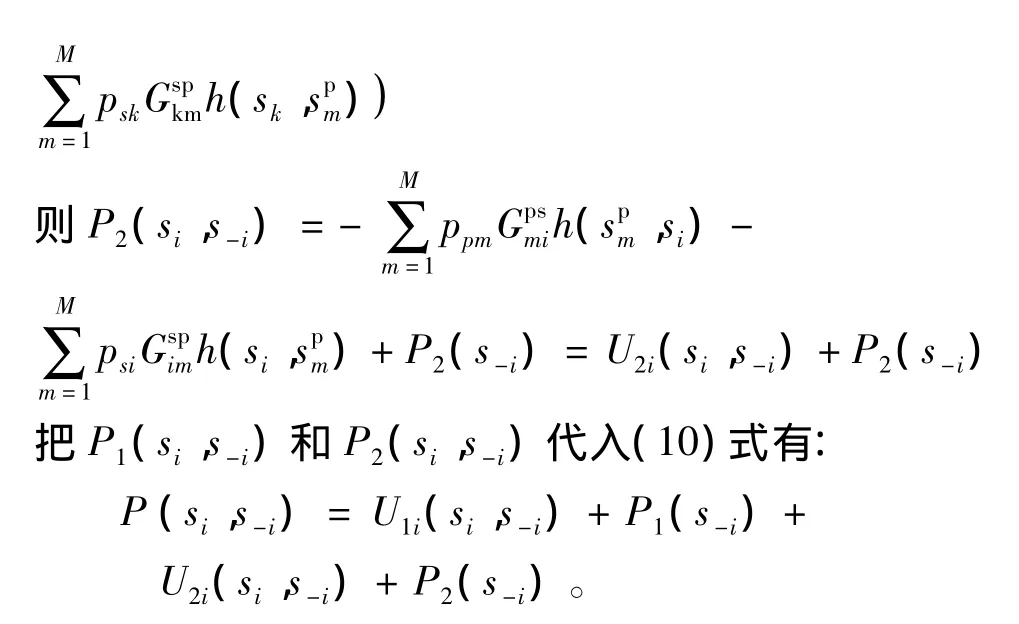
从P2（s－i）的表达式可以看出，P2（s－i）并不受次用户i策略改变的影响。当次用户i从策略si变为s，i时，潜在函数为

证毕，即此博弈为一个潜在博弈，那么该博弈能够收敛于一个纳什均衡。

3 算法步骤

3.1 初始化

随机为N个认知用户分配信道和发射功率。

3.2 迭代

1）次用户按照接入网络的先后顺序依次进行博弈。

2）次用户i的发送端计算Iss'和Isp，并通过公共控制信道将计算出的值告诉其接收端，接收端计算Is's和Ips，并根据接收到的Iss'和Isp计算出使用各信道的效用函数Ui（si，s－i）。

3）次用户i的接收端选取效用函数最大对应的信道，通过公共控制信道告诉其发送端将此信道作为通信信道，即次用户i的新策略

4）重复迭代过程直到算法收敛。

4 仿真分析

在300×300的区域内随机部署N=30个次用户发射－接收对，M=4个主用户发射－接收对，主用户和次用户的发送端到接收端的最大距离为50 m，次用户的发射功率在［1 mw，3 mw］中随机取值，主用户的发射功率在［2 mw，5 mw］中随机取值，噪声功率 σ2=10－9mw。

4.1 算法收敛性

图2为基于潜在博弈的信道分配算法下，各次用户策略变化情况。图2中横坐标为算法执行的次数，纵坐标为各次用户可选择的策略，即可用信道。从图2中可以看出，当算法迭代到60次左右时，次用户的策略不再变化，即达到了均衡状态，这与理论推导结果一致，表明了该算法具有较好的收敛性。

4.2 主用户总吞吐量比较

图3比较了文献［8］算法和本文算法下主用户的总吞吐量。本文设置每个信道的带宽B均为1 MHz，总吞吐量通过）来计算。从图3中可以看出，本算法使得主用户的总吞吐量优于文献［8］。其原因是文献［8］的效用函数仅考虑到了次用户之间的干扰，没有考虑到次用户对主用户的干扰，而本文效用函数的设计考虑了对主用户的干扰。

5 结束语

本文中我们提出了一种改进的认知无线电网络中的频谱分配算法。在实际的认知无线电网络中，主用户和次用户是同时存在的，基于此，本文在效用函数的设计中考虑了对主用户的干扰，以使得次用户在最大化自身效用的同时兼顾了主用户受干扰的情况。文中证明了所构建的博弈模型为潜在博弈，仿真结果显示了算法的收敛特性且在吞吐量性能方面的优越性。

［1］MITOLA J.Cognitive Radios:Making Software Radios more Personal［J］.IEEE Personal Communications，1999，6（4）:13-18.

［2］HAYKIN S.Cognitive Radio:Brain-Empowered Wireless Communications［J］.IEEE JSAC，2005，23（2）:201-220.

［3］XU Xing-kun，WANG Lei.An Adaptive Power Control Algorithm Based on Noncooperative Game Theory［J］.Journal of Beijing University of Posts and Telecommnications，2010，33（4）:135-139.

［4］李校林，柳海涛.基于超模博弈的认知无线电频谱分配算法［J］.重庆邮电大学学报:自然科学版，2010，22（2）:151-155.

LIXiao-lin，LIU Hai-tao.Spectrum allocation algorithm of cognitive radio based on supermodel game［J］.Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition，2010，22（2）:151-155.

［5］ NIYATO D，HOSSAIN E.A Game-Theoretic Approach to Competitive Spectrum Sharing in Cognitive Radio Networks［C］//IEEE WCNC.Hong Kong:IEEE press，2007:16-20.

［6］NIYATO D，HOSSAIN E.Competitive Spectrum Sharing in Cognitive Radio Networks:A Dynamic Game Approach［J］.IEEE Transaction on Wireless Communications，2008，7（7）:2651-2660.

［7］ WU Yong-le，WANG Bei.Repeated Open Spectrum Sharing Gamewith Cheat-Proof Strategies［J］.IEEE Transaction on Wireless Communications，2008，8（4）:1922-1933.

［8］NIE N，COMANICIU C.Adaptive channel allocation spectrum etiquette for cognitive radio networks［C］//IEEE DySPAN，2005.Baltimore:IEEE press，2005:269-279.

［9］NIE N，COMANICIU C.A game theoretic approach to interference management in cognitive networks［EB/OL］.［2011-05-12］.http://www.ece.stevens-tech.edu/～ ccomanic/comaniciu_ima_final.pdf.

［10］ MONDERER D，SHAPLEY L S.Potential game［J］.Journal of Games and Economic Behavior，1996，14（3）:124-143.