基于频谱差异的动态频谱分配博弈算法
2012-06-06张新春何世彪葛利嘉
张新春,何世彪,葛利嘉,孙 江
(1.重庆通信学院,重庆400035;2.海军航空工程学院,烟台 264001)
0 引言
随着无线通信技术的不断发展以及人们对无线通信需求的不断增长,整个无线电频谱空间被划分得所剩无几。然而,从一些研究调查可以看到,频谱资源的缺乏更多是由于对不同无线接入技术的频谱分配不合理造成的,认知无线电技术应运而生。它能够主动检测频谱使用情况,自适应地改变自身通信参数,择机地选择主用户暂不使用的频段进行通信,期望实现高可靠性的通信以及最大化频谱利用率。
目前,认知无线电关键技术包括频谱感知,频谱分配,频谱管理等。本文主要研究频谱感知后的频谱分配问题。把博弈理论引入认知无线电中的动态频谱分配,是一个全新的研究方案,如Nie等人[1]提出了利用潜在博弈(potential game)的自适应信道分配算法,文献[2]提出了多个主系统间频谱价格博弈的伯川德(Bertrand)模型,以及动态博弈的斯坦克尔伯格(Stackelberg)博弈模型等,这些大都是构建特殊的博弈模型来解决频谱分配。
本文在特殊博弈模型静态古诺博弈模型基础上,考虑了频谱的水平差异以及信道容量状况,对其提出了改进算法。
1 系统模型
1.1 认知无线电网络模型
本文分析了有N个用户端设备(customer premises equipment,CPE)的分布式无线通信系统,用户端设备也称认知用户(cognitive user,CU)。
各个认知用户随机的分布在一个网络小区内,独自地感知主网络(primary network)频谱使用状况,相互间通过公共控制信道传递频谱使用信息,然后在相互协商好的信道上进行通信链接,如图1所示。由于博弈理论的特点是各个博弈玩家通过自身所掌握的可用信息选择自己的策略,正是分布式网络的特点。
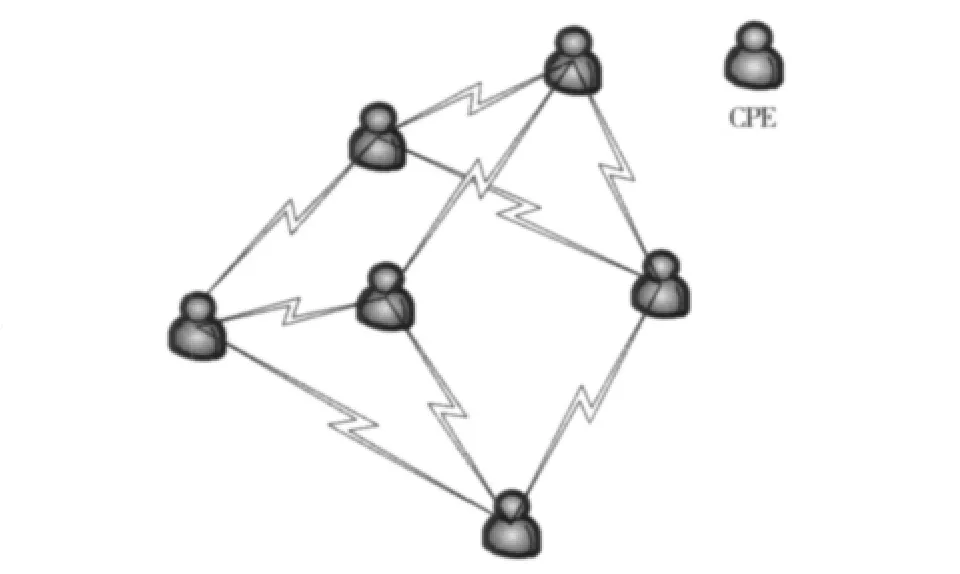
图1 认知无线电网络模型Fig.1 Model of cognitive radio network
1.2 无线传输模型[3]
假设认知用户系统采用自适应调制技术,传输速率基于信道质量可以动态地调整。对于正交幅度调制采用矩形星座图(如4QAM,16QAM),那么其单输入单输出系统在高斯噪声信道的比特错误概率可以近似表示为
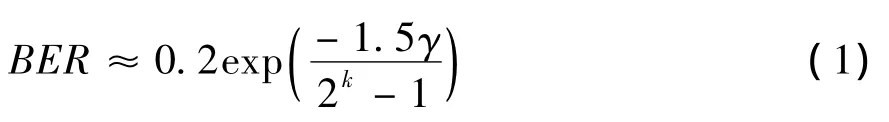
(1)式中:γ表示接收机的信噪比;k代表所用调制方式的频带利用率,且一般为非负值。为保证传输质量,比特误码率应达到一定门限值(BERtari),则认知用户i的频带利用率为

(2)式中,

1.3 博弈模型数学描述
通过1.1节的网络模型描述,我们可以把认知无线电的动态频谱分配问题用博弈过程进行描述。在这个博弈过程中,参与者是认知用户,他们的行动(策略)是对传输信道的选择,并且他们的效用和所选择的信道质量相联系。信道质量信息可由认知无线电用户通过在不同的无线频率上的测量来获得(见1.2 节)。
则频谱分配问题的博弈论模型一般形式为

(4)式中:N是博弈者(也即认知用户)的有限集;Si是相对于博弈者i的策略集,其策略空间为S=×Si,i∈N,则Ui:S→R是效用函数集。在博弈Γ中的每一个博弈者i,效用函数Ui是si和当前其对手的s-i的函数,这里si是博弈者i选择的策略,s-i是其对手的策略。
2 动态频谱分配
2.1 静态古诺博弈模型
目前,认知无线电中常用的静态博弈模型有伯川德博弈和古诺博弈2种。伯川德博弈[2]主要适用于主系统之间的交互,而古诺博弈[4]更适用于认知用户之间的频谱分配过程。
在1.1节所述的系统模型基础上,一个古诺博弈模型表述如下:博弈方是认知用户,每个博弈方的策略相应为分配的非零值的频谱(用bi表示每个认知用户i)。在与其他认知用户以及主用户共享的频谱系统中每个博弈方的支付(payoff)是认知用户的利益(比如收益减去花费,用pi表示)。
对于主系统,假设定价函数(Pricing function)是向认知用户收费,表示为
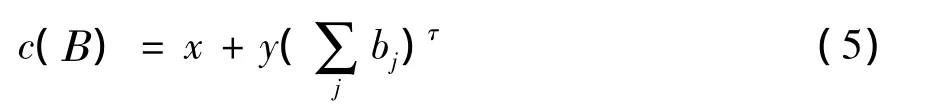
(5)式中:x,y是非零常数;τ≥1确保定价函数为凸函数;Β={b1,…,bN},代表所有认知用户策略集。用ω代表对于主用户来说频谱的价值,于是为了确保主用户愿意共享频谱尺寸(spectrum size)b给认知用户,条件是必要的。另外,主用户向所有认知用户收费是相同的价格。
认知用户i的收益由ri×ki×bi获得,ri表示每单位传输速率认知用户的收益,而获得频谱分配的花费为bi c(b)。于是认知用户i获得的利益将可以表示为
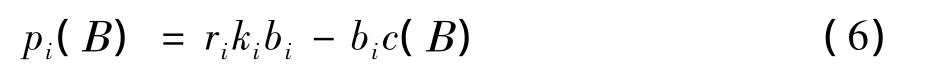
通过(5)和(6)式,可以得到其效用函数为
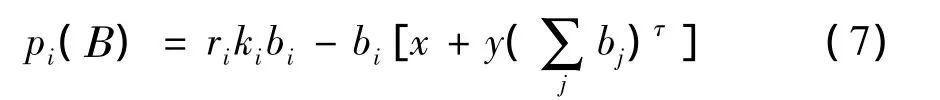
2.2 改进模型
2.1 节的定价函数是把频谱统一进行定价,也即主用户向所有认知用户收费是相同的价格。然而频谱是有区别的。频谱有水平差异和垂直差异2种。水平差异性是指认知用户对不同频谱的偏好不同,也就是即使频谱特性完全相同,也不能相互代替。而频谱的垂直差异指的是频谱的质量差异,如空闲情况以及信道容量状况等。由于频谱的空闲状况已经感知,而信道容量通过认知用户的接收信噪比获得,故本文在考虑频谱的水平差异以及信道容量状况下,对定价函数(5)式改进如下
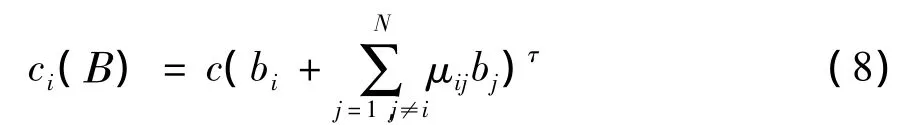
(8)式中:c为非负常数,这里频谱水平差异由频谱相似度矩阵μ描述。μij表示对于认知用户来说,把频谱bj看成bi的相似程度,且 μij∈[-1,1],μij越小,说明两频谱的水平差异越大,当μij=0时,表示频谱bi和bj完全不同,认知用户不能随意更换频谱;μij越大,说明频谱的差异程度越小,当μij=1时,频谱bi和bj完全相同,主用户的要价也就越高,也即文献[4]提到的情况,而当μij<0时,表示频谱bi需要bj的补充,也就是说,频谱bi不足以满足认知用户的需要,需要从另一频谱bj那里获得补充(比如,一个用做上行链路,一个用做下行链路)。可以看出相似度矩阵μ的特点是主对角线上元素为1,其余元素关于主对角线对称。而信道容量由(2)式频谱利用率体现。这样通过(6)式和(8)式,其效用函数改进如下
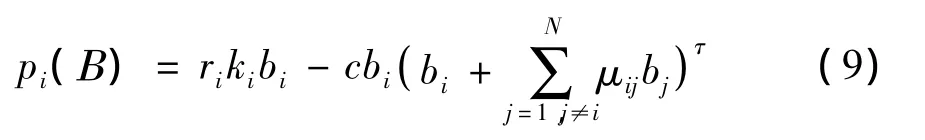
2.3 效用函数的可行性证明
根据纳什均衡点原理[5],如果没有一个参与者能够靠自身行动的改变提高自身收益时,整个参与者集合对应的行动向量就称为纳什均衡。如果满足以下条件,则本文博弈过程就能定性判断纳什均衡存在:
1)认知用户集合是有限的;
2)认知用户策略集Β={b1,…,bN}是封闭的、有界的凸集;
3)效用函数pi(Β)是在行动空间上的连续的拟凹函数。
可行性证明:对于条件1)和2),本文提出的基于频谱差异的古诺博弈模型(spectrum difference based cournot game,SDCG)是显然成立的,下面证明条件3)。
对效用函数进行二次求导有:
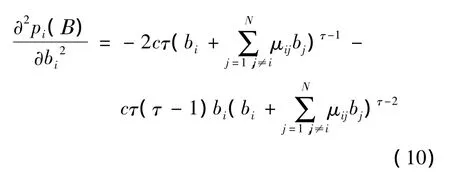
2.4 纳什均衡求解
本文利用反应函数法[6]求解,反应函数法就是参与者根据给定的其他参与者的战略,获得自己的最佳战略。
Β-i==1,…,N;j≠i}表示除了认知用户i的所有策略集合,也即Β=Β-i∪{bi},于是,认知用户i的最佳反应函数为
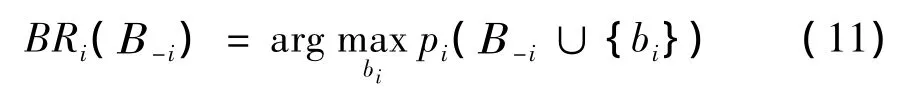
集合Β*={b*1,…,b*N}表示此博弈纳什均衡解,当且仅当

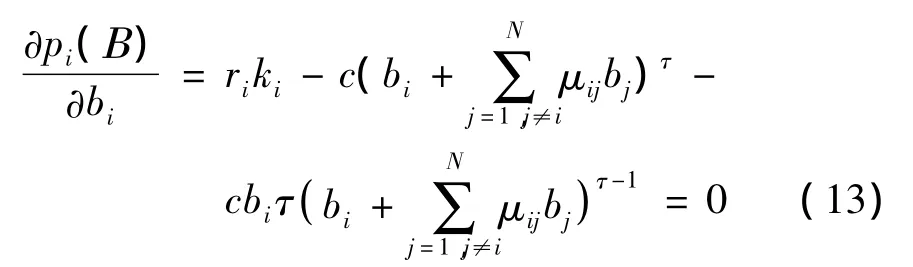
当给定(13)式中所有参数值,求解该方程,即可得到纳什均衡解b*i。
3 性能分析
根据第1部分提出的网络模型,本文考虑了2个认知用户的共享频谱。设定目标BERtari门限值为10-4,定价函数中的常数因子c=1,τ值根据实际测量环境获得(比如线性模型时τ=1),主用户的频谱价值ω=1,每单位传输速率认知用户的收益ri=10。其中一些参数在具体的仿真环境中可能发生变化。
图2给出了2个认知用户的反应函数曲线,2条曲线的交点就是纳什均衡点。从图2中可以看出,每个认知用户的最佳反应是另一个认知用户策略上的线性函数点,2个认知用户的策略bi成逆向变动,当认知用户1的频谱尺寸减小时,认知用户2的频谱尺寸将会增大,反之亦然。当μ=1时,就是经典古诺博弈模型,也就是说文献[4]提出的方法是我们算法的特殊情况。
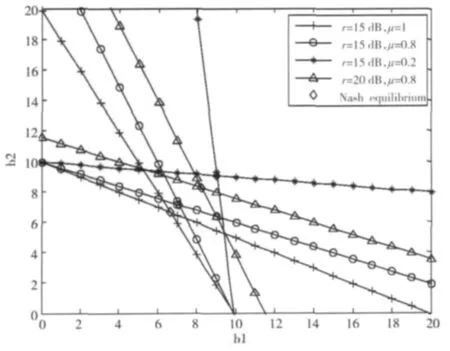
图2 不同条件下的纳什均衡Fig.2 Nash equilibrium in different conditions
由于2个认知用户的效用函数相同,因此图3只给出了1个认知用户的价格(效用)随频谱尺寸变化的曲线。从图3中可以看出,认知用户的利益均在纳什均衡点时达到最大,这与前面的分析是一致的。对比图3中的几条曲线发现,当频谱差异越大时,认知用户的利益就越大,这是因为频谱差异越大时,主用户向认知用户对该频谱的要价就越低,认知用户获得更大的频谱尺寸的同时,认知用户能获得更多利益。同样当μ=1时,就是经典的古诺博弈模型。
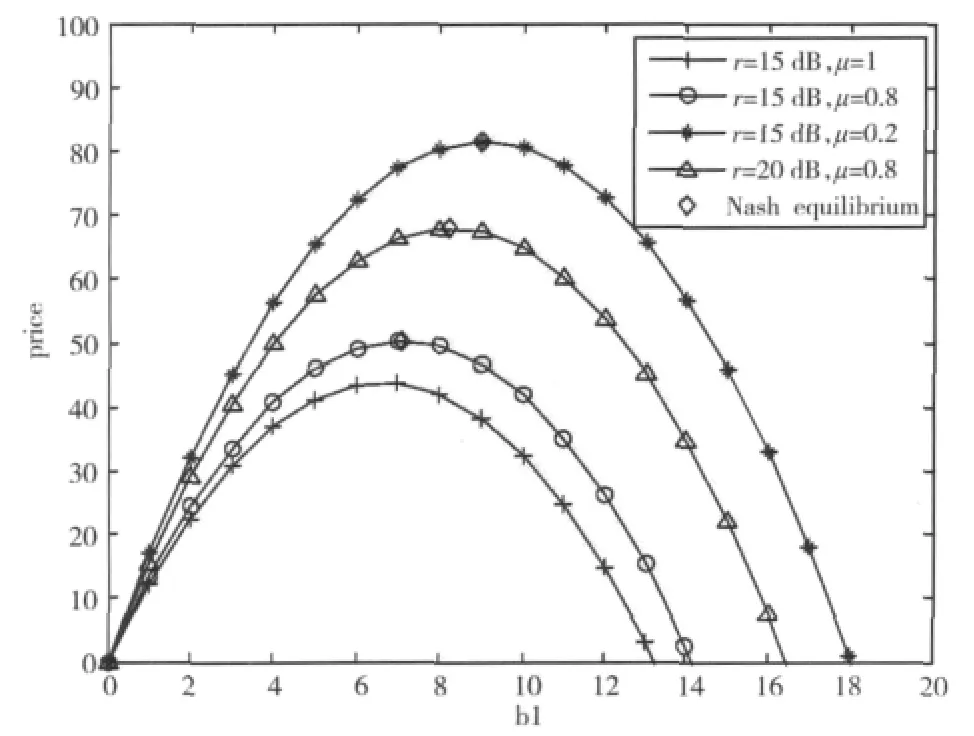
图3 不同条件下的均衡效用Fig.3 Equilibrium utilities in different conditions
4 结束语
本文主要研究了认知无线电中基于博弈论的动态频谱分配算法,重点描述了运用静态古诺博弈模型算法。考虑到实际环境中频谱的差异性,本文对频谱进行了分级,用相似度矩阵进行表示,本文的仿真中已经验证,已有的古诺博弈算法是本文提出算法的一个特殊模式,对已有算法进行了完善和扩充,达到了一定的实际运用能力。
[1]NIE N,COMANIU C.Adaptive channel allocation spectrum etiquette for cognitive radio networks[J].Journal Mobile Networks and Applications,2006,11(6):779-797.
[2]NIYATO D,HOSSAIN E.Competitive Pricing for Spectrum Sharing in Cognitive Radio Networks:Dynamic Game,Inefficiency of Nash Equilibrium,and Collusion[J].IEEE Journal on Selected Areas in Communication,2008,26(1):192-202.
[3]GOLDSMITH A J,CHUA S G.Variable rate variable power MQAM for fading channels[J].IEEE Trans Commun,1997,45(10):1218-1230.
[4] NIYATO D,HOSSAIN E.A Game-Theoretic Approach to Competitive Spectrum Sharing in Cognitive Radio Networks[C]//IEEE Communications Society WCNC 2007.Kowloon:IEEE Press,2007:16-20.
[5] FUDENBERG D,TIROLE J.Game theory[M].Cambridge,MA:MIT Press,1991:23-26.
[6]OSBORNEM J.An Introduction to Game Theory[M].Oxford:Oxford University Press,2003.
