赋β-范线性空间中两种映像的公共不动点的强收敛性定理

董 华

（福建师范大学 数学与计算机科学学院，福建 福州 350007）

赋β-范线性空间中两种映像的公共不动点的强收敛性定理

董 华

（福建师范大学 数学与计算机科学学院，福建 福州 350007）

在赋β-范线性空间中，设计了一种新的关于有限个非扩张映像和有限个一致L-Lipschitzian映像两种不同映像的迭代，在适当的条件下证明了该迭代序列的强收敛性，并且得到了三个推论，本文是一些有关文献的推广。

非扩张映像；一致L-Lipschitzian映像；不动点；赋β-范线性空间

1 引言与预备知识

近年来，在Hilbert空间和一些特殊的Banach空间中，关于有限个非扩张映象迭代序列的逼近问题，许多学者采用各种各样不同的方法在一定的条件下进行了深入的研究。例如，文献［1］是在一致光滑和一致凸的Banach空间中将严格渐近伪压缩映像和非扩张映像结合起来，得到了收敛性定理，文献［2］是在一般的赋β-范线性空间中做了一类映像的迭代逼近，受以上思想的启发，本文在赋β-范线性空间中修改Mann迭代序列，将有限族的非扩张映像Ti和有限族的一致L-lipschitzian映像Si结合起来，给出了一种新的迭代序列，即将文献［1］的空间扩展到赋β-范线性空间，迭代又与文献［2］不同，做出了两类不同映像的迭代，在适当的条件下证明了该序列强收敛于Ti和Si的一个公共不动点，并且得到三个推论，所得的结果推广了有关现有文献的结果。

本文处处假设X是赋β-范线性空间，0≤β＜1，C是X的一个非空闭凸子集，设X*是X的非平凡的对偶空间，＜∵＞表示X和X*间的配对映像，

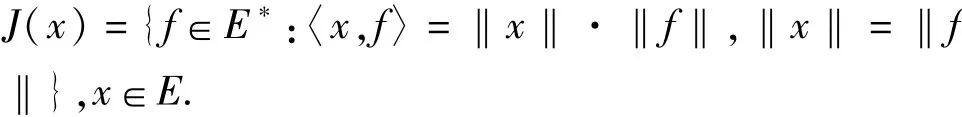
定义1［1］T称为一致L-lipschitzian映像，如果存在一常数L＞0使得‖Tnx-Tny‖≤L‖x-y‖，∀n＞1

定义2［3］如果在线性空间X上定义一个非负函数，记为‖x‖，其满足：

（1）‖x‖≥0且有‖x‖=0⇔x=0

（2）‖x+y‖≤‖x‖+‖y‖

（3）存在数0＜β＜1，使得‖αx‖=｜α｜β‖x‖，∀x∈E，α∈R

则称‖x‖为x的β-范数，空间（X，‖·‖）为赋β-范空间．而X中的一个非空子集D称为β-凸的，如果对∀x，y∈D，s，t∈R且sβ+tβ=1，恒有sx+ ty∈D.

引理1［3］设X是赋β-范线性空间，则对∀x，y∈X，有‖x+y‖2≤‖x‖2+2＜y，j（x+y）＞其中j（x+y）∈J（x+y）为对偶映射．

引理2［4］设｛an｝，｛bn｝，｛δn｝是3个非负实数序列，满足an+1≤（1+δn）an+bn，如果bn＜+∞δn＜+∞，则an=0．

2 主要结果

定理：X是完备的赋β-范线性空间，C是X的闭凸子集，Ti为非扩张映像，Si为一致L-lipschitzian映像，i=1，2，3，…N且Si的值域有界，序列｛xn｝是由下面的格式给出的：

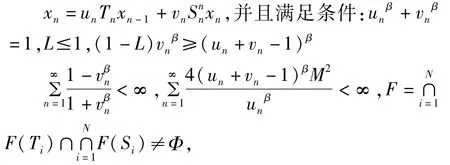
则有结论如下：（1）该迭代是有意义的

（2）｛xn｝是有界的

（3）｛xn｝收敛到Ti与Si的某一公共不动点，p∈F，i=1，2，3…N．

证明：（1）证由下式定义的映像Hn（x）= unTnxn-1+vnSnx，x∈C，Hn∶C→C，n=1，2…是一Banach压缩映像：

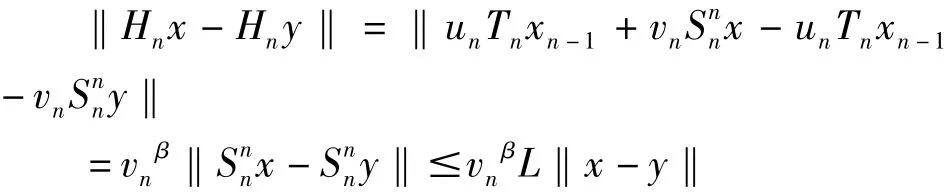
因为L≤1，0＜vn＜1，所以vnβL＜1，那么对每个n= 1，2，3，…N，Hn∶C→C是一Banach压缩映像，那么存在唯一的不动点xn∈C，所以序列｛xn｝是有意义的。

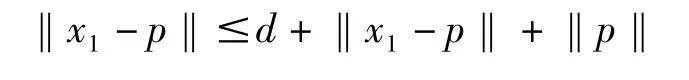
则当n=k+1时，由Ti的非扩张性，Si的一致L -lipschitzian性及定义2中（3），可得

（3）由引理1以及序列｛xn｝的定义得

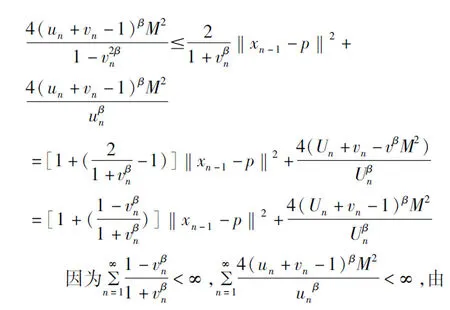
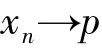
推论1：X是完备的赋β-范线性空间，C是X的闭凸子集，T为非扩张映像，Si为一致L-lipschitzian映像，i=1，2，3，…N且Si的值域有界，序列｛xn｝是由下面的格式给出的：

则有结论如下：（1）该迭代是有意义的

（2）｛xn｝是有界的

（3）｛xn｝收敛到的T与Si的某一公共不动点p∈F，i=1，2，3…N．

推论2：X是完备的赋β-范线性空间，C是X的闭凸子集，Ti为非扩张映像，S为一致L-lipschitzian映像，i=1，2，3，…N且S的值域有界，序列｛xn｝是由下面的格式给出的：

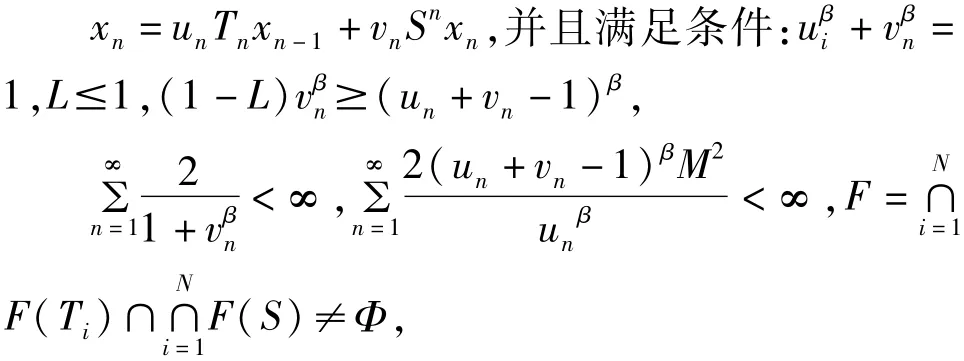
则有结论如下：（1）该迭代是有意义的

（2）｛xn｝是有界的

（3）｛xn｝收敛到的Ti与S的某一公共不动点p∈F，i=1，2，3…N．

推论3：X是完备的赋β-范线性空间，C是X的闭凸子集，T为非扩张映像，S为一致L-lipschitzian映像，且S的值域有界，序列｛xn｝是由下面的格式给出的：

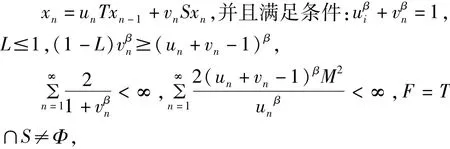
则有结论如下：（1）该迭代是有意义的

（2）｛xn｝是有界的

（3）｛xn｝收敛到的T与S的某一公共不动点p∈F．

3 结论

本文在一般的赋β-范线性空间中修改mann迭代序列，设计了一种有关两类不同映像的新迭代方法，并在适当的条件下证明了该迭代序列收敛于这两种映像的公共不动点，得到了三个推论，本文是有关文献结论的推广。

［1］张石生，黄家琳，王雄瑞.无限族严格渐近伪压缩映像隐迭代程序的强收敛定理［J］.系统科学与数学，2009，29（12）：1613-1621.

［2］严剑龙.赋β-范线性空间中φ-强伪压缩映像迭代逼近的一个注记［J］.武夷学院学报，2010，29（5）：9-11.

［3］朱耿灿，陈丽珍，王建.赋β-范线性空间中渐近伪压缩映像的不动点迭代逼近问题［J］.海南师范大学学报，2009，22（1）：9-12.

［4］Tank K，Xu H K.The nonlinear ergodic theorem for asymptotically nonexpansive mapping［J］.Prco AmerMath Soc，1992，114：399-404.

［5］唐玉超，刘理蔚.赋范线性空间中渐近伪压缩映象的不动点迭代逼近［J］.应用数学学报，2007，30（5）：810-815.

［6］赵良才，张石生.有限簇非扩张映像不动点的黏性逼近［J］.应用数学学报，2008，31（4）：599-607.

［7］李晓南.Banach空间中一致L-李普西兹映射的强收敛问题［J］.苏州科技学院学报（自然科学版），2011，28（1）：1-5.

［8］呈其襄，张奠宙，魏国强，等.实变函数与泛函分析基础［M］.北京：高等教育出版社，2003.

［9］Chang SS.On some problems and results in stuay of nonlinear analysis［J］.Nonlinear Anal TMA，1997，30（7）：4197-4208.

［10］蒋光洁.Banach空间中L-Lipschitzian映射对的公共不动点逼近定理［J］.纯粹数学与应用数学，2010，26（5）：745-750.

［责任编辑 贺小林］

Strong Convergence Theorem of Common Fixed Points of Two Kinds of M appings in Normed Linear Space

DONG HUA
（Department of Mathematics and Computer Science，Fujian Normal University，Fuzhou 350007，China）

The purpose of this paper is to propose a new iterative process for a finite family of nonexpansive mappings and a finite family of uniformly L-Lipschitzianmappings in anormed linear space.Strong convergence of the iterative process is proved in proper condition.Three corollaries are obtained.The results of this paper improve and extend some relative results.

nonexpansivemapping；uniformly L-Lipschitzian mappings；fixed points；normed linear space

O177.91

A

1004-602X（2012）04-0023-03

10.3969／J.ISSN.1004-602X.2012.04.023

2012 09 28

董 华（1986—），女，陕西延安人，福建师范大学在读硕士研究生。