关于不定方程x2+1=Dy3（D∈N）解的存在性讨论

拓小泉，王彩宁，郭金保

（延安大学 数学与计算机科学学院，陕西 延安 716000）

关于不定方程x2+1=Dy3（D∈N）解的存在性讨论

拓小泉，王彩宁，郭金保

（延安大学 数学与计算机科学学院，陕西 延安 716000）

利用初等方法证明了不定方程x2+1=Dy3（D∈N）当D=3，4，5时解的存在性，并在有解的情况下给出了全部解。

最大公因子；互素；解存在性

不定方程在数论中一直引人关注，很多现实问题都可以归结到这类方程的求解的问题上。对于每一个不同的正整数D，形如x2+1=Dy3（D∈N）这类不定方程的解都是确定的。例如，我们知道，D=1时，不定方程x2+1=y3仅有解x=0，y=1［1］；D=2时，不定方程x2+1=2y3仅有解x=±1，y=1［1］。本文利用初等方法来讨论D=3，4，5时，方程x2+1=Dy3解的情况，并证明当D=3，4时无解，D=5时仅有x =±2，y=1整数解。

引理1［1］ξ∈Z［i］是不可约数，即素数，当且仅当（i）N（ξ）=2；（ii）N（ξ）=正有理素数p≡1（mod 4）；或（iii）ξ是正的有理素数p≡3（mod 4）的相伴数。

引理2［1］设M是唯一分解整环，正整数k≥2，以及a，b∈M，（a，b）=，那么，若ab=gk，g∈M，则有a=e1mk，b=e2nk，m，n∈M，其中e1，e2，是M中的单位元素，且e1e2=ek，e为单位元素。

定理1不定方程

无有理整数解。

证明在Gauss数环Z［i］中讨论该方程，它可写成（x+i）（x-i）=3y3。（1．2）

由［1］证明知。d=（x+1，x-i）｜（2x，2i）=2，d =1，1+i，2。而当d=1，1+i，2，方程（1．1）有解时，那么3只能整除（x+i）、（x-i）中之一，但这是不可能的，因为x／3+i／3∉Z［i］或x／3-i／3∉Z［i］．所以方程x2+1=3y3无整数解。

定理2不定方程

无有理整数解。

证明显然x为奇数．在Z［i］中（2．1）可写成

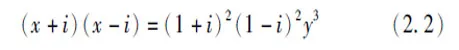
由于d=（x+i，x-i）｜（2x，2i）=2，所以d=1，1 +i，2．当d=1，则（1+i）2（1-i）2=4一定只能整除（x+i）或（x-i），但这是不可能的；d=2也不可能；当d=1+i时，由（2．2）得

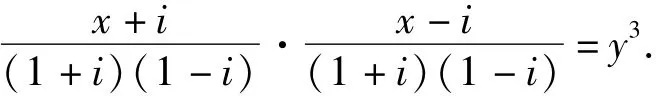
由引理1知x+i，x-i都是素数，所以

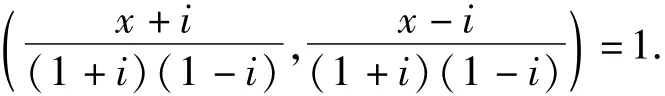
又由引理2知

解之得

x=2（a3-3ab2）

1=2（3a2b-b3），

因为x取奇数，所以原方程无整数解。

定理3不定方程

仅有有理整数解x=±2，y=1．

证明显然x=±1时方程（3．1）无整数解。我们假定x≠±1，在Z［i］讨论方程（3．1），它可以写为

由［1］证明知

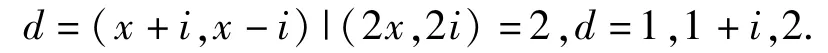
当d=2时，显然不可能，因为x／2+i／2∉Z［i］．

当d=1+i时，推出2=N（d）｜N（x+i）=x2+ 1，可知2不整除x，但是已知x=±2，y=1是（3．1）式整数解，所以d≠1+i，且x只能取偶数．

当d=1时，且5=（2+i）（2-i），由引理1知，

所以

由引理2知x+i=（2+i）（a+bi）3解之得

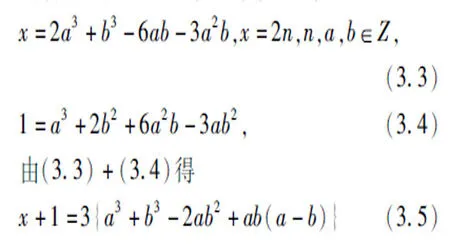
当a，b同时为奇数或为偶数时，等式（3．5）左边为奇数，右边为偶数，x无整数解，则原方程无解；

当a，b一奇一偶时，等式（3．5）左边为奇数，右边为偶数，x无整数解，则原方程无解；

当a=0时，由（3．4）式知1=2b3，x无整数解，则原方程无解；

当b=0时，由（3．4）（3．3）式知a=1，x=2，y=1．

同理，当d=1时，且5=（1+2i）（1-2i）．由引理1知

当a，b同时为奇数或为偶数时，等式（3．7）左边为奇数，右边为偶数，x无整数解，则原方程无解；

当a，b一奇一偶时，等式（3．7）左边为奇数，右边为偶数，x无整数解，则原方程无解；

当b=0时，由（3．6）式知1=2a3，x无整数解，则原方程无解；

当a=0时，由（3．6）式知b=-1，x=-2，y=1．

综上所述定理得证。

推论当D满足引理1条件，由引理2知x2+ 1=Dy3（D∈N）有解则可解出其具体解来，否则可证明其无整数解。

［1］潘承洞，潘承彪.代数数论［M］.济南：山东大学出版社，2001.

［责任编辑 贺小林］

Discussion about the Existence of the Diophantine Equation

TUO Xiao-quan，WANG Cai-ning，GUO Jin-bao
（College of Mathematical and Computer Science，Yan an University，Yan an 716000，China）

Mathematics and By using the elementary method proved that the Diophantine equation when the existence of the solution，and the solution was given under condition of all solutions.

greatest common divisor；goprime；existence of solutions

O156 4

A

1004-602X（2012）04-0007-02

10.3969／J.ISSN.1004-602X.2012.04.007

2012 09 15

陕西省教育厅专项科研项目（07JK430），延安大学2012年研究生教育创新计划

拓小泉（1984—），男，陕西榆林人，延安大学在读硕士研究生。