关于不定方程x2+44=y7

冉银霞

（陇南师范高等专科学校数学系，甘肃 陇南 742500）

关于不定方程x2+44=y7

冉银霞

（陇南师范高等专科学校数学系，甘肃 陇南 742500）

利用初等方法及代数数论的方法讨论了不定方程x2+44=y7整数解的问题，并证明了该方程无整数解.

高次Diophantine方程；整数解；代数数论；整环

设A，B∈N，A无平方因子，关于不定方程

的解的讨论是数论中一类很重要的研究课题。当A=1，B=1时，Lebsgue［1］证明了（1）无整数解。Nagell［2］证明了当A=2，B=1，n=5时，式（1）仅有整数解（x，y）=（±11，3）。对于不定方程（1）当A=1，B=4k，n=7时的解的情况目前研究结果主要有：

（1）当k=1时，方程（1）无整数解；

（2）当k=2时，方程（1）无整数解。

本文研究了当k=4时，方程（1）的解的情况，得到了如下结论：

定理当A=1，B=44，n=7时，方程（1）无整数解．

为了证明定理先给出如下引理：

引理1［5］设M是唯一分解整环，正整数k≥2，以及α，β∈M，（α，β）=1，那么若

αβ=γk，γ∈M，则有α=ε1μk，β=ε2νk，μ，ν∈M，其中ε1，ε2是M中的单位元素，并且ε1ε2=εk，ε为单位元素。

引理2当x为偶数时，不定方程x2+1=26y7无整数解。

证明观察方程可知x≡0（mod2）.那么x2+1≡1（mod2），而26y7≡0（mod2），矛盾，所以不定方程x2+1=26y7无整数解。

下面来完成定理的证明；

定理的证明：先假设x≡1（mod2），在Z［i］中，x2+44=y7可分解为

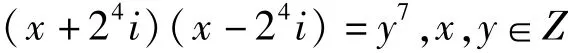
设δ=（x+24i，x-24i），由δ｜（2x，32i）=2知δ只可能是1，1+i，2．由x≡1（mod2）知x+24≡1（mod2），所以δ≠2．若δ=1+i，则2=N（1+i）｜N（x +24i）=x2+28．又x≡1（mod2），所以这样的整数x不存在。因此δ=1，由此及引理1知

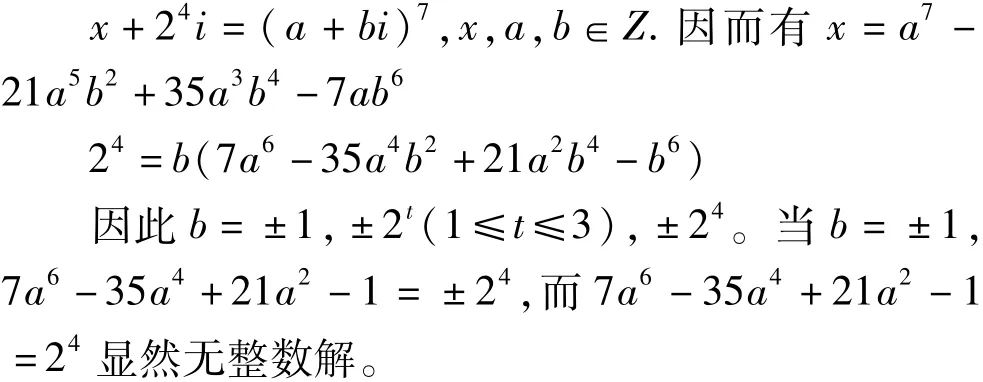
对于7a6-35a4+21a2-1=-24，a必然为奇数，从而x=a2-21a5+35a3-7a为偶数，这与x≡1（mod2）矛盾；

当b=±2t（1≤t≤2），7a6-35a4b2+21a2b4-b6=±24-t，则a必然为偶数从而

x=a2-21a5b2+35a3b4-7ab6一定为偶数，这与x≡1（mod2）矛盾；

当b=24，7a6-35a4b2+21a2b4-b6=1即7a6-35a4b2+21a2b4=224+1，于是一定有224≡-1（mod7）成立，但这与224≡1（mod7）矛盾；

当b=-24，7a6-35a4b2+21a2b4-b6=-1即7a6-35a4b2+21a2b4=224-1，所以a2（7a4-35a2b2+21b2）=32×5×7×13×17×241，因而a2=1或32，代入验证

7a6-35a4b2+21a2b4-b6=-1均不成立。

因此，x≡1（mod2）时，此方程无解。

下面讨论x≡0（mod2）的情况，此时y≡0（mod2），令x=2x1，y=2y1，x1，y1∈Z，则方程可变为x12+43=25y17，显然x1≡0（mod2），再令x1=2x2，此时方程可变为x22+42=23y17，同样再令x2=2x3，此时方程可变为x32+4=2y1

7，最后令x3=2x4，y1= 2y2，此时方程可变为x42+4=26y27，以上x1，x2，x3，x4，y1，y2∈M，由引理2可知该方程无整数解。综上，方程x2+44=y7无整数解。

［1］Lebsgue V A.Surlimpossibiliteen numbers entiers de equation xm=y2+1［M］.Nouv.Amn.Math.1850.

［2］Nagell T.Sur Limpossibilite de quelques equations deux indeterminess［M］.Norsk Marem Forenings Skrifter Senel，1921.

［3］李娜.关于不定方程经x2+4=y7的解［J］.科学技术与工程，2011，11（23）：5613-5614.

［4］高丽，马永刚.关于不定方程x2+6=y7的解的讨论［J］.西南民族大学学报，2008：34（1）：27-29.

［5］潘承洞，潘承彪.代数数论［M］.山东：山东大学出版社，2003.

［责任编辑 贺小林］

On Diophantion Equation x2+44=y7

RAN Yin-xia
（Department of Mathematics，Longnan Teachers College，Longnan 742500，China）

Using the elementary method and algebaic number theroy，we discussed the integer solution of the Diophantine equation x2+44=y7，and it proved this equation has no integer soution.

higher Diophantion equation；integer solution；integer ring；algebraic number theroy

O156.7

A

1004-602X（2012）04-0014-02

10.3969／J.ISSN.1004-602X.2012.04.014

2012 09 10

陇南师范高等专科学校科研项目（2012LSZK02004）

冉银霞（1983—）女，甘肃靖远人，陇南师范高等专科学校讲师，硕士。