组合数运算的一个递推公式

明道忠

（延安大学 数学与计算机科学学院，陕西 延安 716000）

组合数运算的一个递推公式

明道忠

（延安大学 数学与计算机科学学院，陕西 延安 716000）

利用初等的方法给出组合数运算的一个递推公式，并在此基础上得出两个组合恒等式。

：组合数；递推公式；组合恒等式

1 引言与结论

我们熟知的二项式展开式为

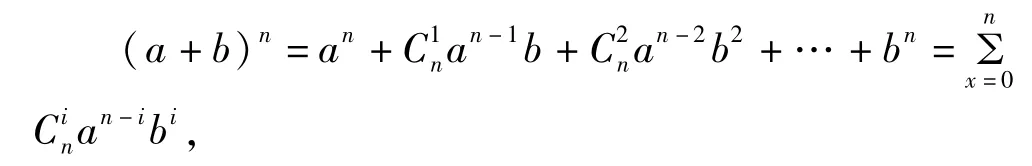
其中Cin称为二项式系数，或称为组合数。

关于组合恒等式，许多组合数学书中都有讨论［1-5］。在上面的二项式展开式中，令a=1，b= -1，得。文献［6，7］将其推广。本文在此基础上，得出一个组合数运算的递推公式。

定理设n，k是自然数，若则有递推公式

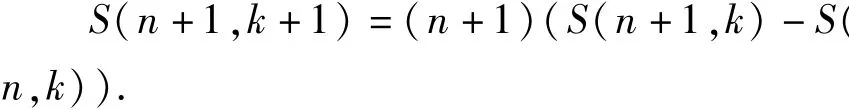
在定理中令k=n，k=n+1得如下组合恒等式。

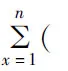
2 定理的证明

证明由熟知的组合数公式Cin+Ci-1n=Cin+1，得

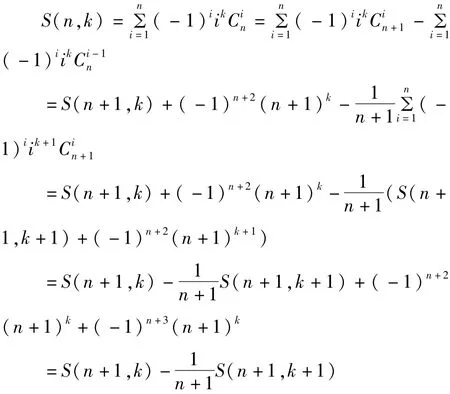
因此，有S（n+1，k+1）=（n+1）（S（n+1，k）-S（n，k）），定理证毕。

在定理中令k=n，则k-1＜n，于是得

同理得S（n，j）=0（j=1，2，…，k-2），即

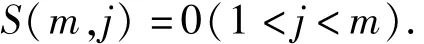
所以，有

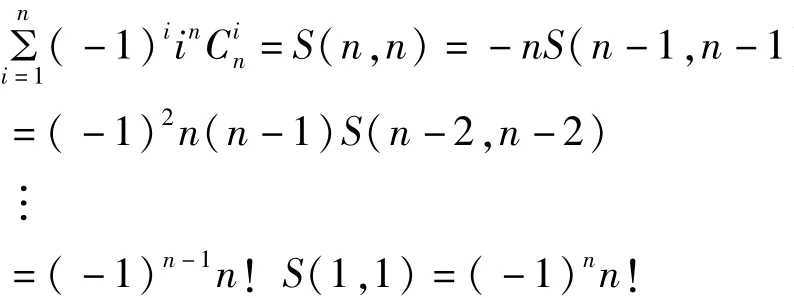
推论1得证。

于是得推论2成立。

［1］孙淑玲，许胤龙.组合数学引论［M］.合肥：中国科技大学出版社，2004.

［2］高丽，杨文芳.组合数的一系列推广的组合恒等式［J］.河南科技大学学报，2006，27（6）：87-89.

［3］屈婉玲.组合数学［M］.北京：北京大学出版社，1999.

［4］高丽，齐琼.关于组合数和的两个递推关系［J］.西南民族大学学报，2010，36（6）：906-907.

［5］姜建国，岳建国.组合数学［M］.西安：西安电子科技大学出版社，2003.

［6］葛如天.关于数学的一项性质［J］.数学通报，2001（6）：155-159.

［责任编辑 贺小林］

A Recursive Formula for Calculating the Combinations Number

MING Dao-zhong
（College of Mathematics and Computer Science，Yan an University，Yan an 716000，China）

Adopted themethod of elementarymathematics，a recurrence formula of combinations number summation was presented.And basing on it，some combinations identity had be obtained.

combinations number；recurrence formula；combinations identity

O157.1

A

1004-602X（2012）04-0026-02

10.3969／J.ISSN.1004-602X.2012.04.026

2012 11 10

陕西省教育厅专项科研计划项目（07JK430）

明道忠（1988—），男，海南屯昌人，延安大学数学与计算机科学学院学生。