子载波间隔对广义多载波水声扩频性能的影响

周锋，尹艳玲，乔钢

(哈尔滨工程大学 水声技术国家级重点实验室，黑龙江 哈尔滨 150001)

对于远程的水声通信，扩频通信已经达到了实用的程度［1-2］，但其通信速率非常低，不能满足未来通信的需要.具有高通信速率的正交频分复用(OFDM)技术越来越多的受到关注，但其面临高峰均比，对频率偏移敏感等问题［3-5］，对于复杂的水声信道，限制了其发展.考虑到二者的优缺点，将二者结合的MC-DS技术起到了折中的作用，广义的MCDS统具有可变的子载波间隔，不同的子载波间隔可以获得不同的扩频增益和载波信号之间的频谱交叠.水声信道可以看做是一个梳状滤波器［6］，对于多载波通信来说，子载波间隔的选取和水声信道的相干带宽有关，MC-DS系统可以很方便地调整子载波间隔和扩频增益来获得更好的通信性能.

为了了解MC-DS系统在水声通信中的性能，文中用Matlab仿真了在水声多途信道和高斯白噪声信道下，该系统误码率随子载波间隔变化的曲线，得到了一个最优的子载波间隔，并通过水池试验验证了该结论.

1 系统模型

1.1 发射信号

广义MC-DS系统的发射机框图如图1所示［7］，对于M进制相位调制，比特周期为Tb的原始数据流经过串/并转换后变成U个低速子数据流，符号周期Ts=UTblbM，每个低速子数据流通过时域扩频码ck(t)进行扩频，之后在U个子载波上分别调制.基于图1，发射信号［8］可以表示为

式中:P是每个子数据流的发射功率;bu(t)=为第u个子数据流的二进制数据;bu［n］为等概率取值+1或－1的随机变量;pτ(t)为矩形波;c(t)为时域扩频码，且对于所有的子载波而言，该扩频码相同.c(t)可以表示为

其中，cj取+1或－1，ψ(t)为时域扩频序列的码片波形，该波形定义在［0，Tc)上，其归一化为∫Tc0ψ2(t)dt= Tc.最后，在式(1)中，φu为第u个载波调制的初始相位.

图1 广义MC-DS发射机框图Fig.1 Block diagram of the generalized MC-DS transmitter

广义MC-DS的频谱如图2所示，图中Ws=2/ Tc1表示系统可以利用的带宽，Tc1为一个对应的单载波扩频信号的码片持续时间，WDS=2/Tc表示每个DS扩频子载波信号的零点到零点带宽，Tc为码片持续时间.相邻子载波的频率间隔为Δ=λ/TS，λ是归一化子载波间隔，调整λ，可以改变子载波间隔.根据图2，有以下关系式:

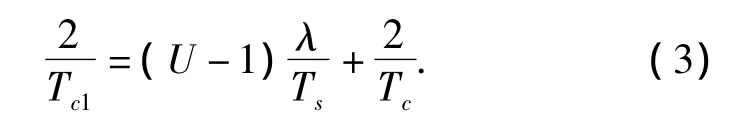
图2 广义MC-DS的频谱Fig.2 Spectrum of the generalized MC-DS

定义Ne=Ts/Tc为广义MC-DS系统中的子载波信号的扩频增益［7］，N1=Tb/Tc1为对应的单载波扩频系统的扩频增益.将Ts=UTblbM=UN1Tc1lbM和Ts=NeTc代入式(3)，广义MC-DS系统中的每个子载波信号的扩频增益可以表示为

从上式可以看出，对于给定的带宽W，子载波个数U和确定的调制方式，扩频增益Ne随归一化子载波间隔λ的增大而减小.当λ=1时为多音MCDS系统，当λ=Ne时为正交MC-DS系统.

1.2 相关接收机

MC-DS系统的相关接收机结构框图如图3所示，在多途信道下，选择输出器选择输入信号幅度最大的支路进行解调，对于加性高斯白噪声(AWGN)信道，对接收的信号同步后直接解调.假设接收机实现了理想的载波同步、定时同步和采样率同步等.

当发射信号经过AWGN信道时，接收到的复基带等效信号可以表示为

式中:n(t)为零均值、双边带功率谱密度为N0/2的加性高斯白噪声.假设接收端每个载波码片波形的匹配滤波器时域冲激响应为ψ*(Tc－t)，对匹配滤波器的输出波形以码片速率采样，则第一个发送符号的第u个子载波上的第n个观测样本可以表示为

将式(5)代入式(6)，yu，n可以表示为

其中，Nu，n是均值为零每维方差为 N0/2Eb的复AWGN采样值.

式(7)中，IBIu，n是由其他子载波传输除bu［0］以外其他数据比特所引入的干扰，可以表示为

式中:Δfiu=fi－fu=λ(i－u)/Ts，Δφiu=φi－φu.从式(9)可以看出，干扰项IBIu，n和载波相位φ、码片波形ψ和归一化子载波间隔λ有关.因为φ是随机变量，因此，最小化载波间干扰就是选择合适的码片波形和优化子载波间隔.文献［8］证明了若使用矩形码片波形且λ取整数，或者使用一般的码片波形，λ取整数并使1－exp(j2πnΔfiuTc)≠0时，载波间干扰可以消除.

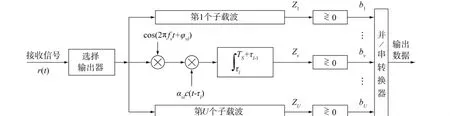
图3 广义MC-DS的相关接收机Fig.3 Related receiver of the generalized MC-DS

1.3 性能分析

文献［8］给出了单用户多载波DS-CDMA系统在频率选择性衰落信道下的BER性能，文中假设每个子载波信号经历的是平坦衰落，即单个子载波信号的带宽低于无线信道的相干带宽.而对于水声信道来说，相关带宽要比空中无线信道小得多，因为水声信道的多途时延比较大，对于浅海信道来说，其多途扩展有时可达到几百毫秒［3］.这时信道的相干带宽只有几到十几赫兹，而扩频后的子载波信号的带宽一般为几十到几百赫兹，甚至达几千赫兹.因此，应该考虑单个子载波信号也受到频率选择性衰落的情况.

考虑时不变系统，时不变水声信道模型为

式中:alp与τlp分别为第lp条路径的复增益和时延，共Lp条离散路径.则MC-DS信号经过上述信道后接收信号可以表示为

式中:n(t)为零均值、双边带功率谱密度为N0/2的加性高斯白噪声.接收机选择输出信号幅度最大的路径(假设为第l条路径)进行解调.如图3所示，假设接收机能够实现码同步，则不妨设τ1=0.设发射的第一个符号为bv(v=1，2，…U)，为了检测该数据比特，相应的判决变量可以表示为

其中，将式(11)代入式(12)中，Zv可以表示为

式中:Nvl由式(11)中的n(t)决定;Nvl是均值为零、方差为的高斯随机变量，Eb=PTs代表每个数据比特的能量.Dvl为期望输出，结合式(11)和式(12)且设lp=l，u=v，可以得到

其中，bu［－1］和bu［0］分别表示第u个子载波所传输的前一个和当前的数据比特;θvlp=φvlp－φvl是均匀分布在［0，2π)上的随机变量;R(τlp)和(τlp)分别为扩频序列波形c(t－τ)和c(t)的部分码片互相关函数:

最后，式(13)中多载波干扰项可以表示为

由于第u和第v个载波的频率fu和fv不同，所以重新定义c(t－τ)和c(t)的部分相关函数:

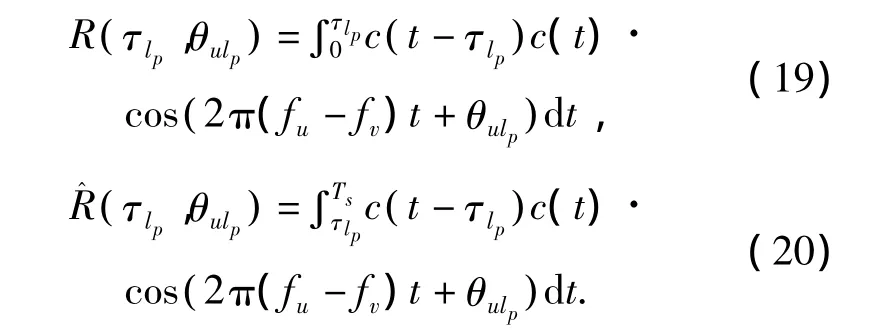
上面分析了式(13)中的干扰项，为了讨论系统的误码性能，下面分析一下这些干扰项的统计特性.容易看到，当u=v时，I(s)1=I(s)2，因此只需讨论I(s)2的统计特性即可.假设信源由独立同分布的二进制比特构成，基于标准高斯近似理论［9-10］多载波干扰(multi-carrier interference，MCI)项I(s)2可以近似为零均值方差为式(23)所示的高斯随机变量:

其中，Ωulp=E[(aulp)2]，由文献［10］可得

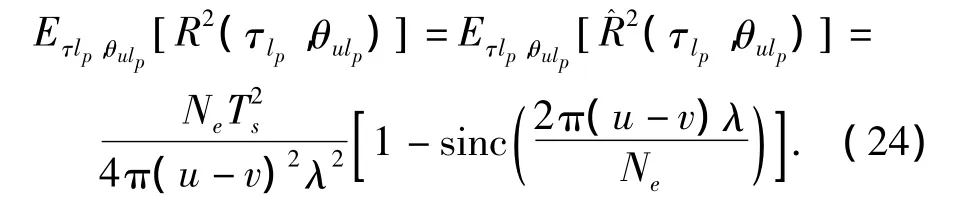
将式(24)代入式(23):

令u－v=x，则

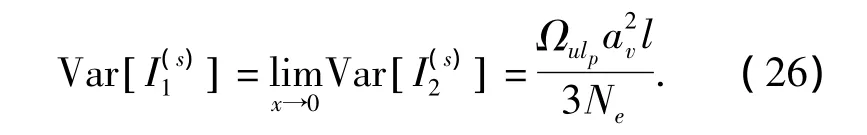
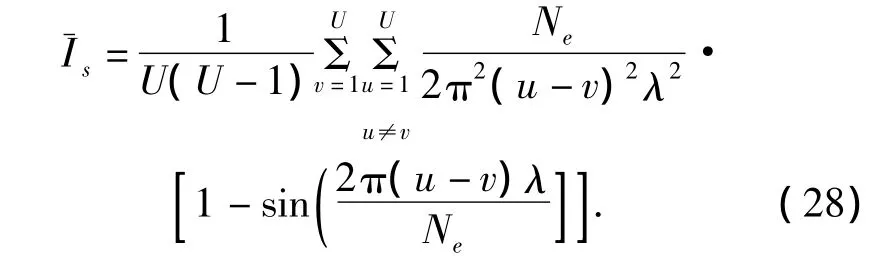
假设多径强度分布(multipath intensity profile，MIP)服从负指数分布，即Ωulp=Ωoexp(－ηlp)，η＞0，且对于不同的子载波处的抽头强度是独立的随机变量，则式(27)可以重新表示为

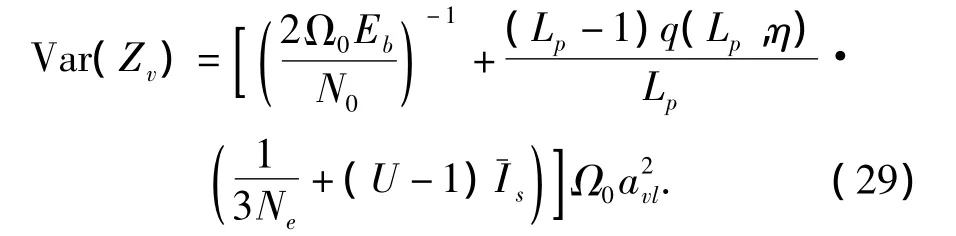
其中，q(Lp，η)=(1－e－ηLp)/(1－e－η)，推导上式过程中，Ωul由其均值代替，即Ωul=q(Lp，η)/Lp.

由以上推导，可以得到Zv(v=1，2，…U)是均值E［Zv］=bv［0］和方差如式(29)所示的高斯随机变量.对于给定的衰落幅度aul(l=0，1，…L－1)，QPSK调制的MC-DS系统的误码率可以表示为

其中，

Q(x)代表高斯Q函数，经典定义为［11］

则MC-DS系统的平均BER可以表示为

式中:f(γ)是γ的功率谱密度.

从分析可以看出，MC-DS系统在多途信道中的平均BER除了和信号与噪声的功率有关外，还和多途信道的路径数、衰落幅度、归一化子载波间隔有关.由于水声信道尚无统一的建模方法，很难给出f(γ)，所以文中不给出BER的闭式解，下节结合不同的水声信道条件给出仿真的结果.

2 MC-DS系统在水声信道中的性能

2.1 仿真结果

通过Matlab仿真研究在高斯白噪声信道和水声多途信道下MC-DS系统随载波间隔变化的误码性能.上节分析了系统在两种信道的误码率和哪些因素有关，现给出不同信道条件下的仿真结果.图4给出了在高斯白噪声信道下，归一化子载波间隔λ对MC-DS系统BER性能的影响，其中，仿真参数为:单载波扩频系统的扩频增益N1=32，子载波个数U=7，系统带宽 B≈2～4 kHz，调制方式为QPSK，扩频码片波形为矩形，根据式(4)，可得正交时系统的归一化子载波间隔λ=112.

图4 AWGN信道下，MC-DS系统BER性能Fig.4 The BER performance of the MC-DS system in AWGN channel

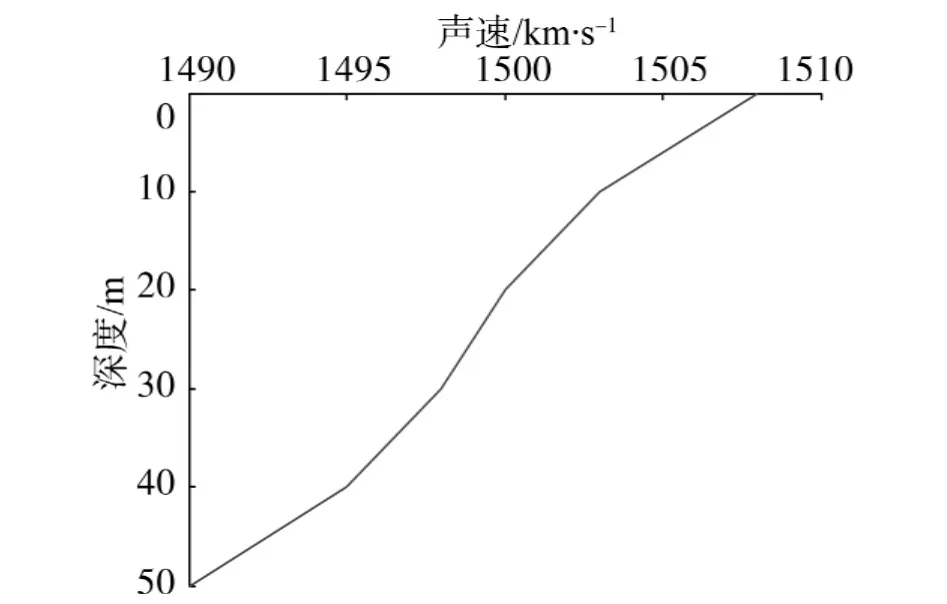
图5 浅海信道声速分布Fig.5 The sonic speed distribution of the shadow sea channel

从图4可以看出，在AWGN信道下，BER随λ变化较为平稳，无明显的起伏，此时多音MC-DS具有更明显的优势，因为可以容纳更多的载波，从而承载更多的信息.

对于水声多途信道，主要讨论了浅海信道下MC-DS系统的误码性能.仿真的浅海信道声速分布如图5所示，采用某软件仿真的浅海水声信道［12］，模拟海深约为50 m，声源位于水平距离0 m、垂直深度20 m的位置，接收水听器位于水平距离5 km、垂直深度18 m的位置，仿真获得的信道冲激响应如图6所示.

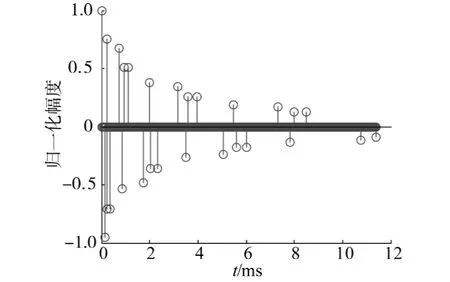
图6 浅海水声信道冲激响应Fig.6 The impulse response of the shadow sea channel

图7 浅海信道下系统的BER曲线Fig.7 The BER curve of the system in the shadow channel

在水声多途信道下，MC-DS系统的BER随归一化子载波间隔λ变化的曲线如图7所示，从图中可以看出，BER随λ的变化有明显的起伏，在多音时出现了一个极小值，同时在正交附近，小于正交时又出现了一个次极小值，系统的误码率同时受扩频增益和子载波之间的频谱交叠程度影响，调整λ来最小化载波间干扰，当二者达到一个平衡点时，将会使系统的误码率达到最小，这时的λ称为最优的子载波间隔λopt，至于最小值出现在何处，与水声多途信道的结构有关，从仿真结果来看，两个极小值点出现在多音和正交附近.

2.2 水池实验结果

为了验证MC-DS系统在水声信道中的性能，在哈尔滨工程大学信道水池进行了试验.该水池有效长度为45 m，宽6 m，水深5 m，四周布有吸声尖劈，池底为沙底，接收与发射换能器均无指向性，位于水池中央位置，深度均为2 m，相距约15 m，通过发送LFM信号测试信道的冲激响应如图8所示.

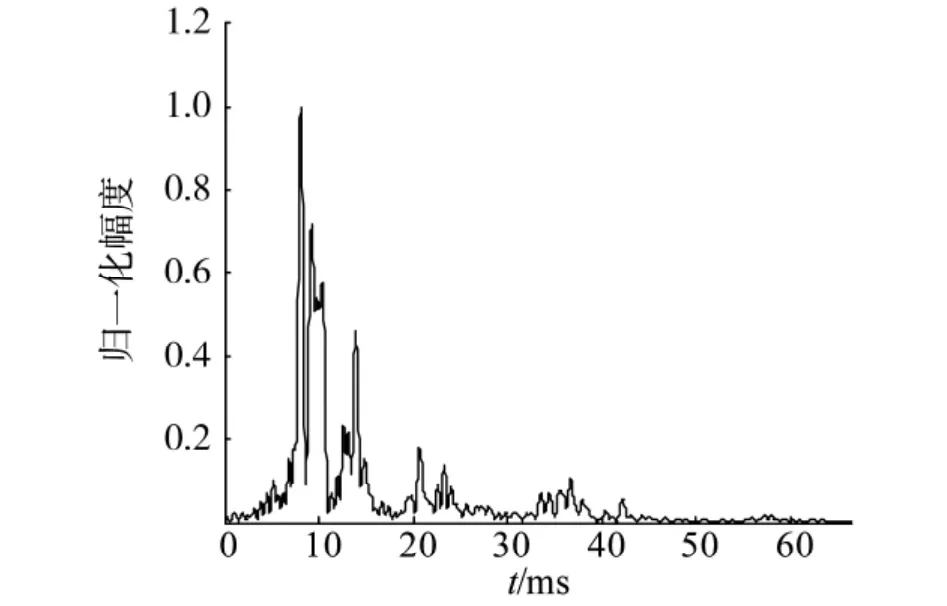
图8 水池信道冲激响应Fig.8 The impulse response of the pool channel

图9 水池信道下系统的BER曲线Fig.9 The BER curve of the system in the pool channel

为了得到MC-DS系统在水池信道下的BER随子载波间隔变化的趋势，利用测试的水池信道冲激响应作为仿真信道，仿真结果如图9所示，仿真参数为:N1=32，U=7，B为6～8 kHz，调制方式为QPSK，扩频码片波形为矩形.从图10中可以看到BER在多音时出现了极小值，正交附近出现一个次极小值，但多音时的BER要低于正交时的BER，图10给出了载波数分别为8、7、4时的水池试验结果，相对应的正交归一化载波间隔为114、112、102.

从接收信号的星座图可以看出，在λ多音时星座图比较收敛，在λ=50和正交时星座图比较发散，主要是由于随着载波间隔的增大，子载波的带宽减小，不同载波受到不同程度的衰落，导致接收信号能量的分散.从图10(d)水池信道的幅频响应可以看出，在发射信号频带内信道的最大衰落达15 dB，而且随着子载波间隔的增大，扩频增益减小.虽然子载波间隔的增大可以减小频谱交叠，抑制载波间干扰，但是扩频增益的减小对系统性能的影响起主要作用，二者之间的权衡受多途信道的影响.对比仿真的浅海信道和水池信道下的误码率曲线，可以看到水池信道下，多音时获得的优势更明显，是因为水池多途信道要比仿真信道简单，最大多途时延比较小，多途干扰比较小，因此引起的载波间干扰比较小，这时扩频增益对误码性能的影响起主要作用.

图10 水池试验结果Fig.10 The experimental results in the pool

3 结束语

文中分别讨论了在水声多途信道和高斯白噪声信道下，MC-DS系统的误码性能随子载波间隔变化的趋势.从仿真和水池试验结果可以看出，在多途干扰比较小或高斯白噪声信道下，多音MC-DS更占优势，因为此时的载波间干扰较小，影响系统的主要因素是扩频增益，多音时获得了更大的扩频增益.同时在正交时出现了一个次极小值，对于多途干扰比较严重的水声信道，多音时频谱严重混叠，扩频增益获得的优势不如减小码元长度带来的优势大，误码率极小值可能出现在正交附近.因此，可以得出结论，无论在何种信道下，总会有一个最优的子载波间隔使系统的性能最优，这个最优的子载波间隔会随信道的变化而变化.

［1］艾宇慧.M序列扩频谱水声通信研究［J］.哈尔滨工程大学学报，2000，21(2):15-18.

AI Yuhui.The study of M sequence spread acoustic communication［J］.Journal of Harbin Engineering University，2000，21(2):15-18.

［2］李霞，姜卫东，方世良，等.水声通信中的多载波CDMA［J］.声学技术，2005，24(4):202-205.

LI Xia，JIANG Weidong，FANG Shiliang，et al.Multi-carrier CDMA in underwater acoustic communication［J］.Technical Acoustics，2005，24(4):202-205.

［3］徐小卡.基于OFDM的浅海高速水声通信关键技术研究［D］.哈尔滨:哈尔滨工程大学，2009:30-31.

XU Xiaoka.The study of the key high speed acoustic communication technology in the shadow sea based on OFDM［D］.Harbin:Harbin Engineering University，2009:30-31.

［4］张海滨.正交频分复用的基本原理与关键技术［M］.北京:国防工业出版社，2006:6-7.

ZHANG Haibin.Basic Principe and key technology of OFDM［M］.Beijing:National Defense Industry Press，2006:6-7.

［5］HENRIK S，CHRISTIAN L.Theory and applications of OFDM and CDMA-wideband wirelesscommunications［M］.(s.l.):John Wiley＆Sons Ltd，2005:145-166.

［6］惠俊英.水下声信道［M］.北京:国防工业出版社，1992:56-65.

HUI Junying.Underwater acoustic channel［M］.Beijing: National Defense Industry Press，1992:56-65.

［7］YANG L L，HANZO L.Performance of generalized multicarrier DS-CDMA over Nakagami-m fading channels［C］// IEEE Trans Commun，2000:956-966.

［8］张有光，潘鹏，孙玉泉.多载波通信［M］.北京:电子工业出版社，2010:97-100

［9］PURSLEY M B.Performance evaluation for phase-coded spread-spectrum multiple-access communications–Part I: System analysis［J］.IEEE Transactions on Communications，1977，25(8):795-799.

［10］YANG L L，HANZO L.Overlapping M-ary frequency shift keying spread-spectrum multiple-access system using random signature sequences［J］.IEEE Trans.Veh.Technol.，1999，48(16):1984-1995.

［11］PROAKIS J G.Digital communications［M］.3rd ed.New York:McGraw-Hill，1995.

［12］范敏毅.水下声信道的仿真与应用研究［D］.哈尔滨:哈尔滨工程大学，2000:26-46.

FAN Minyi.A study on simulation＆application of underwater sound channel［D］.Harbin:Harbin Engineering University，2000:26-46.