近似到O(μ2)阶完全非线性的Boussinesq水波方程
2012-04-13刘忠波房克照邹志利
刘忠波,房克照,2,邹志利
(1.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024;2.河海大学 海岸灾害及防护教育部重点实验室,江苏南京210098)
作为近岸海域强有力的波浪数值计算模型之一:Boussinesq类水波方程得到空前的发展[1-11],当前研究和应用以二阶Boussinesq方程居多,其中以Wei G等[4]给出的以波面和水深某一处速度表达的高阶Boussinesq方程最具代表性,其精确到O(μ2)阶完全非线性.而以水深积分平均速度表达的Boussinesq方程多以弱非线性或近似到O(εμ2)阶非线性为主,即便有近似到O(μ2)阶完全非线性的Boussinesq方程[5],其在O(μ2)阶非线性项中也部分地忽略了水深对空间坐标的导数.为使得此类Boussinesq方程在近似到O(μ2)阶具有完全非线性的同时具有良好的色散性能,本文从Madsen给出的近似到O(μ2)阶完全非线性Boussinesq方程(其色散性与经典Boussinesq方程一致)出发[1],对动量方程进行加强,得到一组改进的高阶Boussinesq水波方程.讨论了加强后方程与其他Boussinesq方程之间的异同,从理论和数值2个方面对加强后方程进行考察,对比分析本文加强方式和传统加强方式对数值结果的影响.
1 理论推导
1.1 水波方程的导出
文献[1]从Laplace方程出发,给出了一组近似到O(μ2)完全非线性的Boussinesq水波方程,方程以波面升高η和水深积分平均速度u=(u,v)表达,其二维无因次形式为[1]
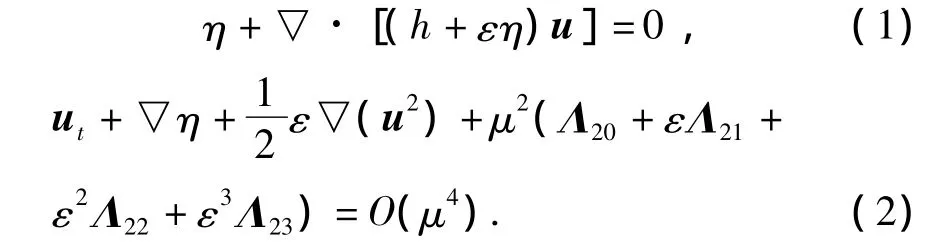
其中,
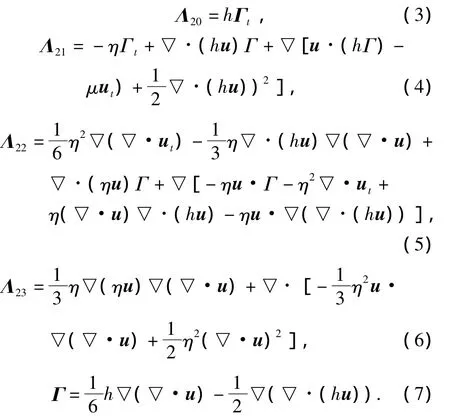
式中:h为静水深,▽=(∂x,∂y)为二维偏微分算子,下标t表示变量对时间的导数.
以上方程色散精度与经典Boussinesq方程一致,为拓展其适用水深,引入:

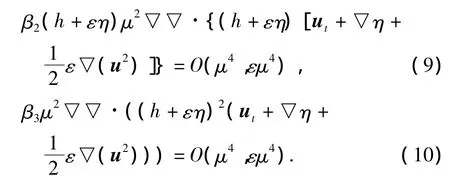
将式(8)~(10)添加到方程(2)左端,方程可写成如下形式:
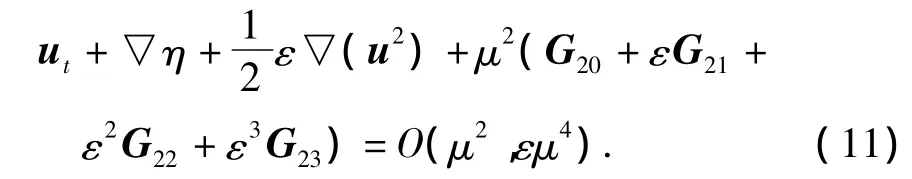
式中:G20、G21、G22、G23为O(μ2)阶线性项和非线性项出:
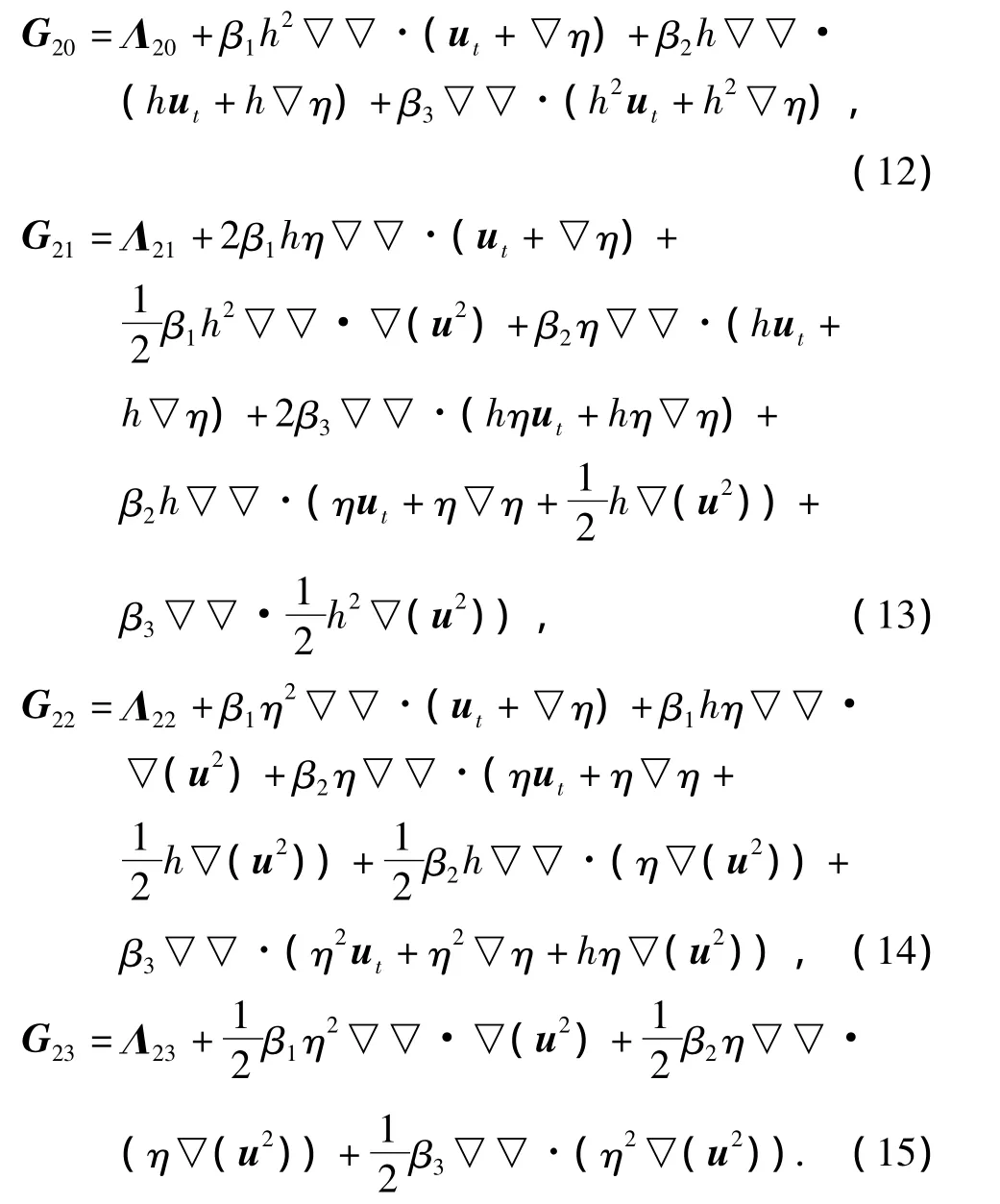
方程(1)、(11)构成了一组新的、近似到O(μ2)阶完全非线性的Boussinesq水波方程(以下简称方程一).而传统改进此类方程的方式则引入如下表达式:
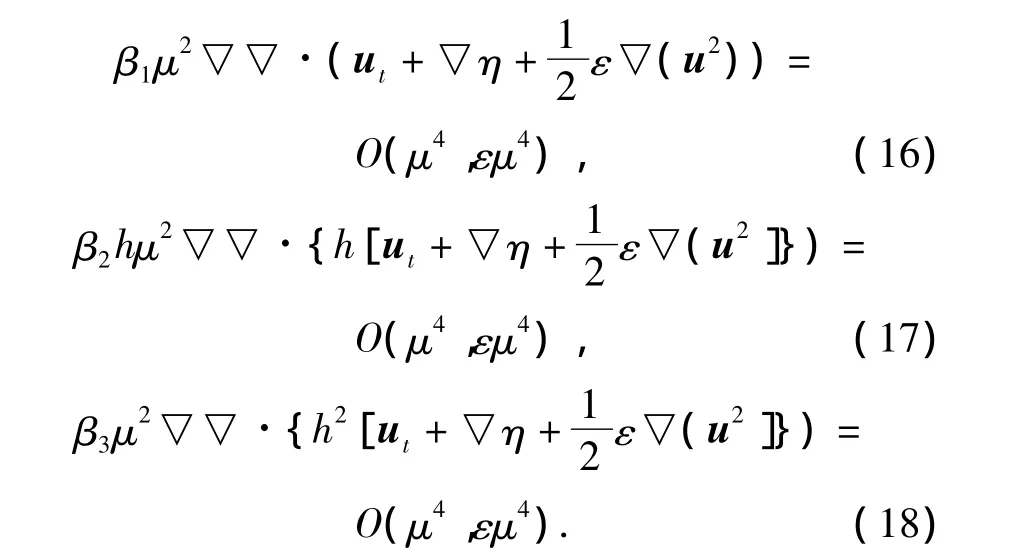
式(16)~(18)中不仅有色散性项,还有水流存在下引起波浪色散关系变化的多普勒效应项.将式(16)~(18)引入到方程(2)中,方程仍可写成式(11),且G20保持不变,但非线性项变为
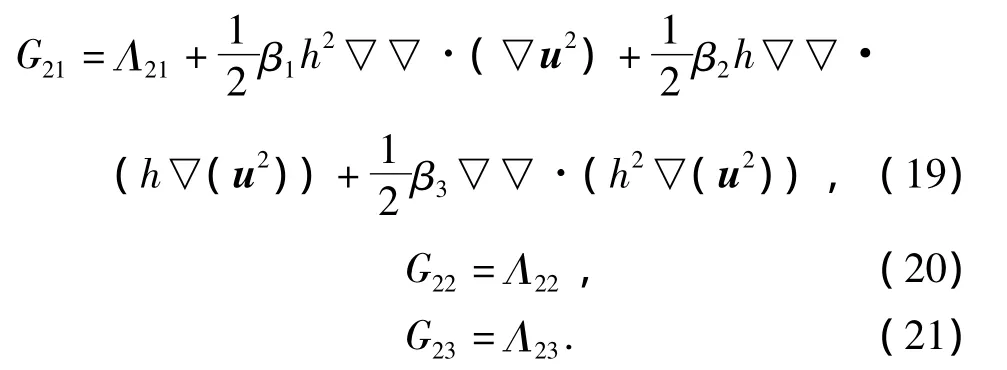
当式(11)中非线性表达式由式(19)~(21)表达,其和方程(1)构成另外一组方程(简称方程二),对比2方程的表达式可以发现,2种改进方式在色散性和变浅性性能方面是一致的;不同之处在于第一种方式多考虑了多项非线性项,如εμ2中多了类似hη▽▽·(ut+▽η)的项.
1.2 方程一与其他方程的比较
1.2.1 与文献[6]的比较
选取参数值为β1=0.033,β2=-0.1,β3=0并忽略O(μ2)阶非线性项,即取G21、G22、G23为0,方程可转化为文献[6]方程;若不忽略O(μ2)阶非线性项,相当于其方程被拓展到近似在O(μ2)阶完全非线性.
1.2.2 与文献[7]的比较
选取参数值为 β1=-29/885,β2=0,β3=-2/59,方程在色散性方面可等同于文献[7].2个方程的主要差别有2点:1)O(μ2)阶非线性项中关于水深对空间变量的导数上略有差异;2)O(μ2)阶非线性项中,本文方程增加了一些项,如在G21中增加类似hη▽▽·(Ut+▽η)的项.
1.2.3 与文献[8]的比较
选取参数值为β1=-0.001 3,β2=-0.065 4,β3=0,并忽略O(μ2)阶非线性项,即取G21、G22、G23为0,方程可转化为文献[8]的方程;若不忽略二阶非线性项,相当于原方程被拓展到近似在O(μ2)阶完全非线性.
1.2.4 与文献[9]的比较
文献[7,9]只是通过改变参数值的方法拓展了的方程,方程的色散适用水深略微改善.当本文取β1=-0.024 7,β2=0,β3=-0.032时,并忽略G21、G22、G23中的部分项,可转化为该方程.
1.2.5 与文献[10]的比较
文献[10]从欧拉方程出发重新推导了近似到O(εμ2)阶的一维Boussinesq方程,并增加了类似式(9)且以通量形式表达以提高色散性.尽管方程是从欧拉方程出发,但其仅含O(εμ2)非线性项.当本文方程取 β1=0,β2= -1/18,β3=0,并忽略O(ε2μ2)O(ε3μ2)阶项,并写成一维形式后,二者具有较强的可比性.
2 性能分析
采用文献[1]的分析方法,利用Maple软件符号运算功能,可方便地对上述方程进行线性性能(包括色散性和变浅作用性能)和非线性性能(包括二阶谐波波幅A2递函数和三阶谐波波幅A3)分析[1,7].
2.1 色散性及变浅作用性能
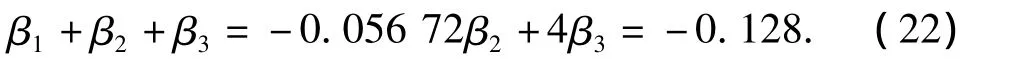
方程一和方程二具有相当的色散性,其与参数的选取有关,当参数选取合理的情况下,可使方程的相速度以及群速度在较大范围内与解析解误差较小.研究发现,当选取的参数值满足以下关系时,对应方程的无因次相速度(C*)、无因次群速度()以及变浅作用系数(Cs)具有较高的精度,其与解析解的对比见图1~3.由式(22)给出的2个表达式中含有3个未知参数,并不能给出具体值,需要通过非线性性能的比较加以确定.
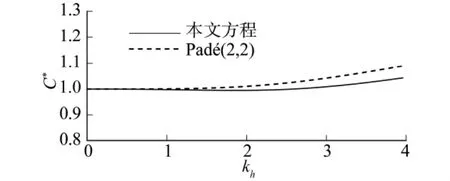
图1 方程的无因次相速度Fig.1 Nondimensional phase velocity of the equations

图2 方程的无因次群速度Fig.2 Nondimensional group velocity of the equations
由图1可见,当kh=4时,本文方程的相速度误差在5%以内,而线性Stokes波色散关系的Padé(2,2)展开对应的误差为10%;由图2可见,当kh=2.6时,本文方程的群速度误差在5%以内,而线性Stokes波色散关系的Padé(2,2)展开对应的误差为13.5%.由图3可见,本文方程的变浅作用系数与解析解在kh<3范围内也吻合较好.

图3 方程的变浅作用系数Fig.3 Nondimensional shoaling coefficient of the equations
2.2 非线性性能
研究发现,无论参数怎么变化,方程一的二阶谐波波幅保持不变,这是因为G21中▽▽·(ut+▽η)项前的系数:-2.5β2-β1-4β3=-(β1+β2+β3+ 0.75(2β2+4β3))=0.152 7是常数.此外仅当某一参数取超过1后,方程一的三阶非线性性能有所改善,这已无实际意义.故本文仅取特殊情况:β=0.007 3,β2=-0.064,β3=0下方程一和方程二的二阶谐波波幅和三阶谐波波幅,具体情况见图4.可见:当且仅当kh很小时(kh<0.5),方程一和方程二的二、三阶波幅传递函数有可比性,随着水深变大,方程一的二阶非线性和三阶非线性均优于方程二的性能.

图4 方程一和方程二的无因次二、三阶传递函数值Fig.4 The second-,and third-order transfer functions for two equations
3 数值格式以及计算结果讨论和分析
针对一维有因次形式的方程一,在非交错网格下进行离散,采用五点中心差分(边界点采用五点偏心)格式近似变量的空间导数,采用三阶预报-四阶校正的线性多步模式进行时间积分[12].通过结合文献[13]的内部造波法和2个计算域末端设置海绵吸收层的方法实现波浪的无反射入射.针对文献[14]进行的潜堤上波浪传播的物理模型实验进行数值模拟.实验中有3组波浪要素,这里选取2种波况进行模拟,分别为工况A(波高H=0.02m,周期T=2.02s)和工况C(波高H=0.041m,周期T=1.01s),二者对应的无因次水深kh分别为0.67和1.69.模拟时,时间步长取为0.01s,空间步长取0.025 m,波浪场达到稳定状态后取计算数据进行分析.
3.1 两种不同改进方式对计算结果的影响
为考察2种不同改进方式对计算结果的影响,采用方程一、二分别求解波浪运动.图5给出工况A各次谐波幅值的数值计算结果和实验数据的比较.由图可见,在基频和倍频的沿程波幅变化对比中,方程一、二给出相近的数值模拟结果,且均与实验数据吻合较好,但是在三倍频和四倍频的波幅变化对比中,方程一计算结果与实验数据吻合程度更佳.图6给出工况C各次谐波幅值的数值计算结果和和实验数据的比较.由图可见,在基频的沿程波幅变化对比中,方程一、二给出数值结果相近,但是在倍频和三倍频的波幅变化中,方程一能给出更好的结果,而在四倍频的波幅变化中,尤其在潜堤后,二者给出的波幅均小于实验值.
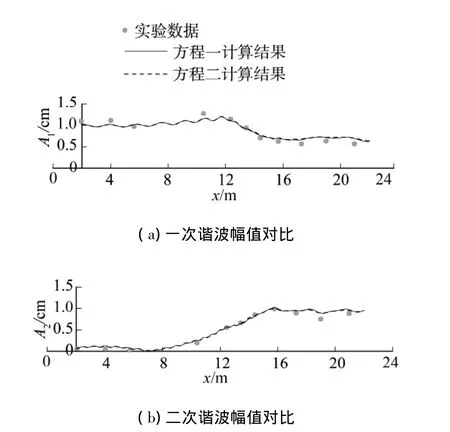
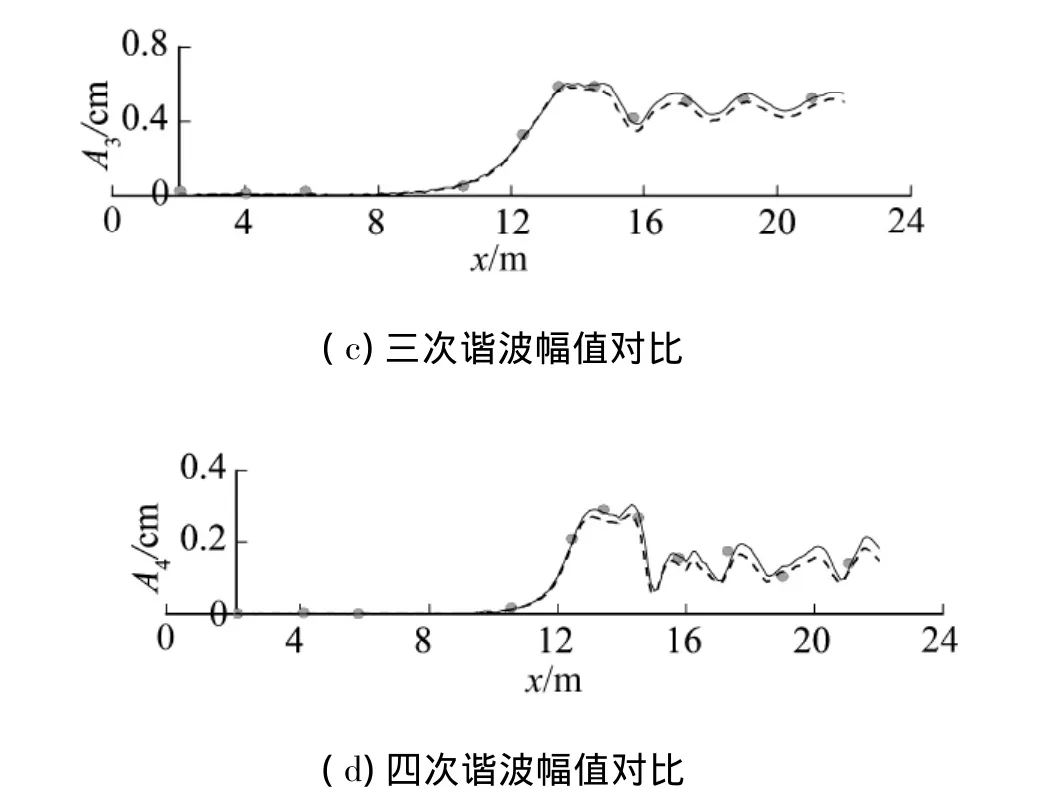
图5 数值计算的各次谐波与实验结果的对比(工况A)Fig.5 Comparisons of computed harmonics amplitudes and experimental data for case(case A)
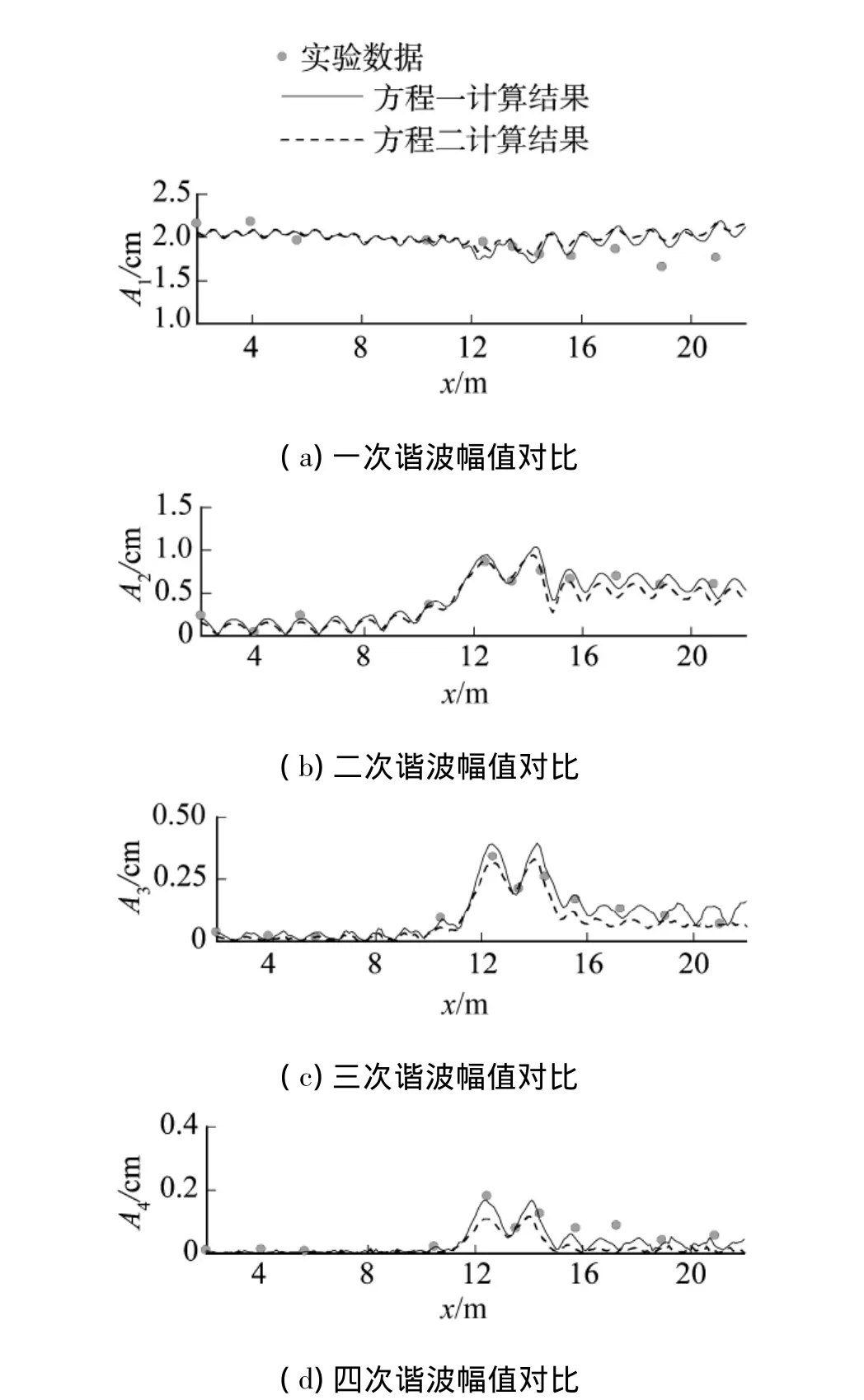
图6 数值计算的各次谐波与实验结果的对比(工况C)Fig.6 Comparisons of computed harmonics amplitudes and experimental data for case(case C)
以上2种波况都得出同样的结论,方程一模拟结果比方程二模拟结果更佳,这与前面理论分析的结论是一致的.此外,数值结果也侧面反映出第一种改进方式比传统的仅改善色散关系及水流存在下引起多普勒效应的方式更具有代表性.
3.2 不同非线性精度对数值结果的影响
为了验证方程一精确到不同非线性精度对数值计算结果的影响,在编制程序时,在不同阶非线性项前预设多个参数,当这些参数值均取1.0时,代表考虑全部阶非线性,而当高阶非线性项前系数取0时,则代表仅考虑不同低阶非线性精度,这里给出利用非线性精度精确εμ2(中等非线性模型)及ε3μ2阶(完全非线性模型)模拟工况A的数值计算结果与实验结果的对比,具体见图7.由图7可见,在基频和倍频的沿程波幅变化对比中,包含完全非线性项的作用并不明显,结果相近,但是在三倍频和四倍频的波幅变化中,尤其在潜堤后,完全非线性模型给出结果优于后者,这表明完全非线性特征的存在对于准确描述高阶谐波有重要作用.
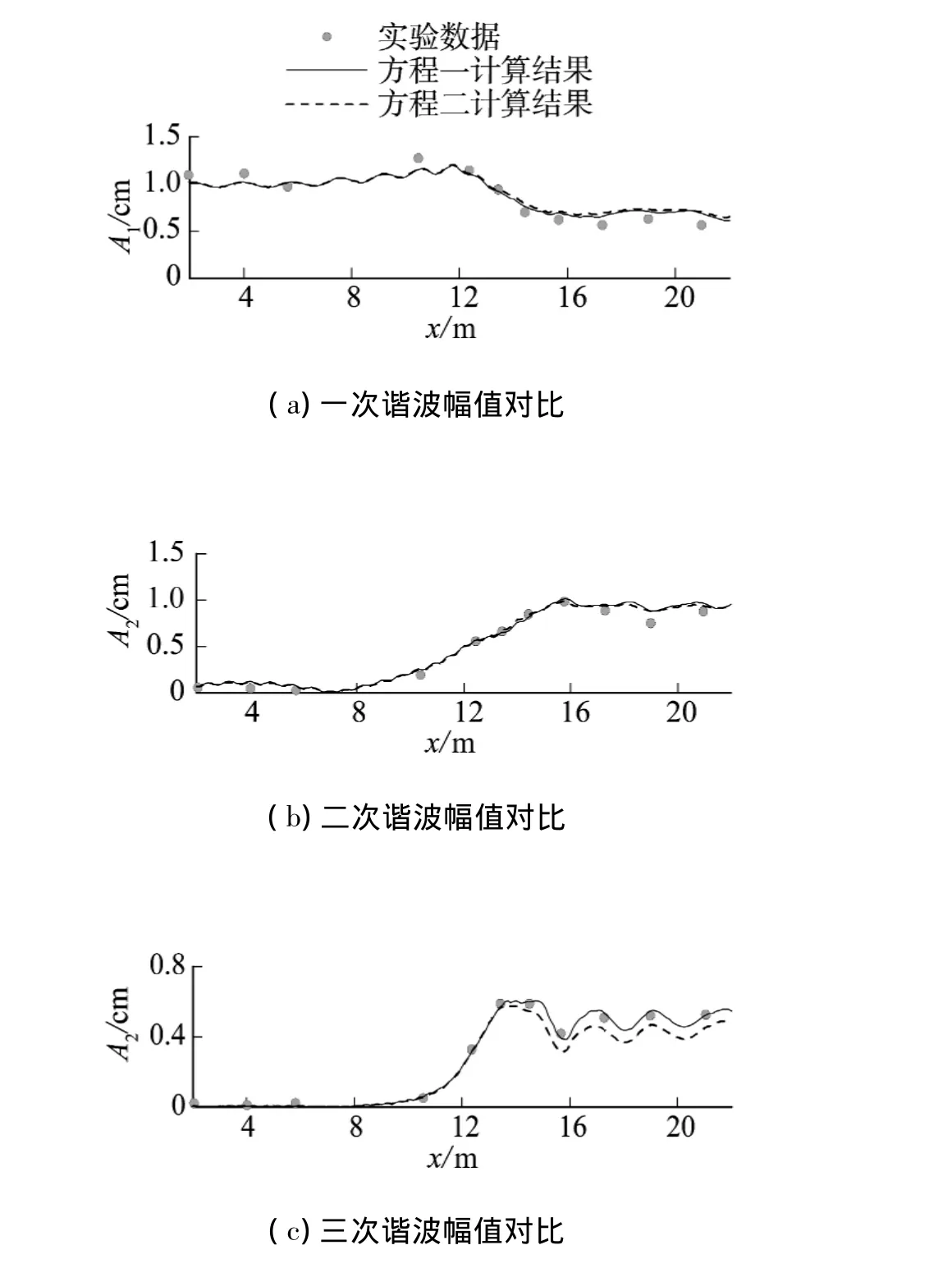
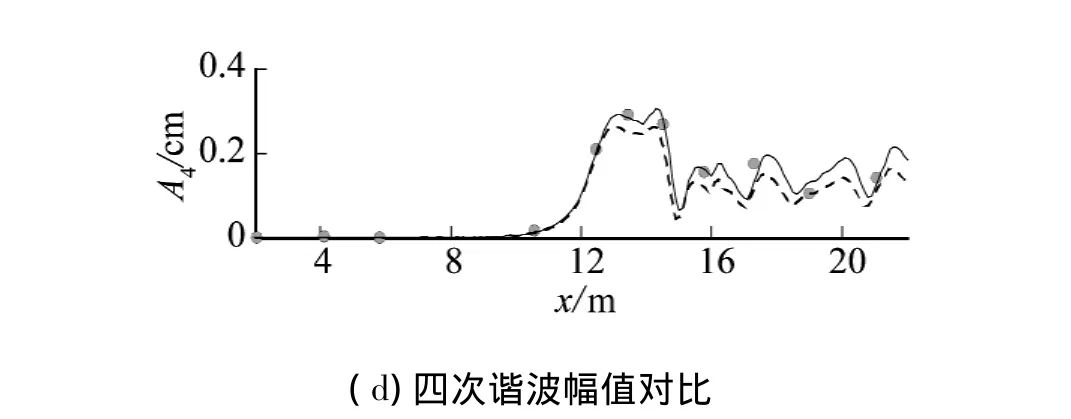
图7 不同非线性精度时的模拟结果对比(工况A)Fig.7 Comparisons of computed harmonics amplitudes with different nonlinear accuracy(case A)
4 结论
通过改进Boussinesq水波方程,得到了一组近似到O(μ2)阶完全非线性的高阶Boussinesq水波方程.改进过程中保留强非线性项,而传统改进方式仅局限于改进方程色散性能,针对上述2种方式给出的方程进行了理论分析和数值计算,得到以下主要结论:
1)第1种改进方式,其不仅包含了第2种传统的改进方式,且比第2种改进方式在非线性性能方面更佳.在相关文献中,尤其以水深积分平均速度表达的方程中,以第2种方式改进居多,这实质上只是为了改善色散性和变浅性能,而未以改善非线性性能为目的,这是需要特别注意的.
2)本文方程相速度在5%误差内,最大适用水深kh=4,而线性Stokes波色散关系式的Padé(2,2)逼近所对应的方程最大适用水深kh=3.14;就本文研究的结果来看,方程一给出的数值结果优于其他方程,这说明非线性越强,数值结果越好.
此外,本文的改进方式可为相关Boussinesq类水波方程在改善非线性的方面提供重要参考.
[1]MADSEN P A,SCHAFFER H A.Higher-order Boussinesqtype equations for surface gravity waves:derivation and analysis[J].Philosophical Transactions of Royal Society of London Series A——Mathematical Physical and Engineering Sciences,1998,356:3123-3184.
[2]MADSEN P A,SORENSEN O R.A new form of the Boussinesq equations with improved linear dispersion characteristics,Part 2.A slowly-varying bathymetry[J].Coastal Engineering,1992,18,183-204.
[3]NWOGU O.An alternative form of the Boussinesq equations for near shore wave propagation[J].Journal of Waterway,Port,Coastal and Ocean Engineering,1993,119(6):618-638.
[4]WEI G,KIRBY J T,GRILLI S T,et al.A full nonlinear Boussinesq model for surface waves.I:highly nonlinear,unsteady waves[J].Journal of Fluid Mechanics,1995,294:71-92.
[5]邹志利.高阶Boussinesq水波方程[J].中国科学(E辑),1997,27(5):460-473.
ZOU Zhili.Higher order Boussinesq equations[J].Science in China(Series E),1997,27(5):460-473.
[6]BEJI S,NADAOKA K.A formal derivation and numerical model of the improved Boussinesq equations for varying depth[J].Ocean Engineering,1996,23(8):691-704.
[7]邹志利.水波理论及其应用[M].北京:科学出版社,2005:428-429.
[8]刘忠波,张日向,姜萌.简便推导改进Boussinesq方程的一种方法[J].大连理工大学学报,2005,45(1):118-120.
LIU Zhongbo,ZHANG Rixiang,JIANG Meng.A simple method for deriving improved Boussinesq equations[J].Journal of Dalian University of Technonlogy,2005,45(1): 118-120.
[9]王诺,刘忠波,佟士祺.二阶Boussinesq水波方程色散性的修正[J].水运工程,2008,410(8):1-5
WANG Nuo,LIU Zhongbo,TONG Shiqi.A modification of linear dispersion property of second order Boussinesq equations for water waves[J].Port and Waterway Engineering,2008,410(8):1-5.
[10]张殿新,陶建华.一种改善了非线性和色散性的Boussinesq方程模型[J].应用数学和力学,2008,29(7): 813-824.
ZHANG Dianxin,TAO Jianhua.A Boussinesq model with improved nonlinearity and dispersion[J].Applied Mathematics and Mechanics,2008,29(7):813-824.
[11]邹志利.适合复杂地形的高阶Boussinesq方程[J].海洋学报,2001,23(1):109-119.
ZOU Zhili.Higher order Boussinesq equations for rapidly varying topography[J].Acta Oceanologica Sinica,2001,23(1):109-119.
[12]刘忠波.高阶Boussinesq方程的研究[D].大连:大连理工大学,2006:45-47.
[13]WEI G,KIRBY J T,SINHA A.Generation of waves in Boussinesq models using a source function method[J].Coastal Engineering,1999,36:271-299.
[14]LUTH H R,KLOPMAN G,KITOU N.Kinematics of waves breaking partially on an offshore bar,LDV measurements of waves with and without a net onshore current[R].Netherlands:Delft,1994.
