基于CFD的大型风力发电机组叶片气动性能研究

盛振国，李陈峰，任慧龙，刘小龙

(1.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001;2.中国船级社 产品设计评估中心，北京 100006;3.中国船舶科学研究中心，江苏 无锡 214082)

随着能源和环境问题日益突出，储量丰富、无污染、可再生的风能逐渐受到人们的重视［1］.风力发电机是将风能转换为电能的机械装置，叶片是其重要组成部分.叶片以及叶轮的气动性能直接决定了风力发电机组的效率.目前，国内外有关大型风力发电机组叶片气动性能研究有风洞试验和数值模拟两种方法［2-3］.风洞试验数据可靠，但成本高、周期长，且单个获得的流场信息有限.数值模拟方面，主要借鉴螺旋桨理论，建立了经典的叶素动量理论［1］(blade element-momentum，BEM).目前大多风力机气动性能计算软件是基于叶素理论开发的，叶素理论实质上是把叶片当作标准的二维问题来处理，难以真实地反映翼型的三维旋转效应和动态失速等影响.随着计算机技术的发展以及三维湍流技术的提高，计算流体力学方法(CFD)在研究复杂流场特性中起着越来越重要的作用，但在风机气动性能研究中的应用仍处于起步阶段［4］.Sorensen等［2-3］使用不可压缩RANS方法预报了风机叶片的性能，与试验结果吻合较好.Madsen等［5］研究了偏航对气动负荷的影响.与BEM相比，CFD方法可以考虑三维旋转效应引起的失速延迟现象和动态失速的影响，直接获得翼型的三维气动特性和风轮周围详细的流场特性，尤其对于新翼型的设计，不需要经验值，即可得到功率特性.

根据大型风力发电机组叶片的特点，采用CFD技术，基于RANS方法耦合SSTk-ω湍流模型，建立了风机叶片气动性能分析方法，给出了二维翼型和三维叶轮气动性能分析的网格生成、边界条件与数值求解方法等.采用本文方法对NACA64-618翼型的二维气动性能和2MW风机叶片三维气动性能进行了分析，与试验值及GHBladed软件计算结果的比较证明了有关方法的准确性，在此基础上对2MW风机翼型进行了优化，完善了其气动性能.

1 风机气动性能的CFD数值模拟技术

1.1 控制方程

流体连续性方程和RANS方程如下:

式中:ui、uj为速度时均量;为速度脉动量;ρ为密度;μ为流体粘性系数;p为压力.其中，对于二维问题，i=1，2;三维问题，i=1，2，3.

由于风机叶轮为三维旋转对称结构，因此将控制方程转化到旋转坐标系下.对于静止坐标系下的描述速度场的绝对速度V与旋转坐标系下描述速度场的相对速度Vr之间的关系如下:

式中:Ω为指角速度向量(即旋转坐标系的角速度);r是旋转坐标系中的位置向量.

连续性方程:

动量方程:

式中:τ是应力张量，它包含粘应力和湍流应力2部分.对于湍流应力项采用涡粘性进行描述，即:

式中:μt为涡粘性系数，计算采用Spalart-Allmaras湍流模式.

1.2 SSTk-ω湍流模型

对于翼型气动性能的 CFD分析，SSTk-ω模型［6］是常用的湍流模型之一，它混合了k-ω模型和k-ε模型，使得该湍流模型同时具有了k-ε模型计算近壁面区域粘性流动的可靠性和模型计算远场自由流动的精确性.

式中:Γk和Γω为扩散系数，μt为涡粘性系数，Gk和Gω为湍流产生项，Yk和Yω为湍流耗散项，α*为低雷诺数修正系数，σk和σω分别是k和ω对应的湍流普朗特数，Dω为扩散项.

2 二维翼型气动性能分析

风力机叶片都是三维的，但是数值计算中三维计算所需的网格数较多、占用的计算机资源较多、计算周期较长.为了计算快捷，工程中很多计算都以二维翼型为研究对象，将空间流动简化成了平面流动.

2.1 二维翼型气动性能分析参数设置

2.1.1 坐标系定义

坐标原点角度的定义如图1所示.所有坐标以弦长为特征长度进行无量纲化，因此，翼型前端为x=－0.5，翼型后端为x=0.5.

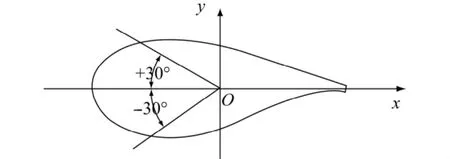
图1 坐标系的定义Fig.1 Definition of coordinates

2.1.2 网格生成与控制

在数值计算中，计算网格的质量直接影响到计算结果的精度和收敛性.对于二维翼型分析，采用的网格种类为多块结构化网格，网格数量控制在6× 104左右.在靠近翼型处网格适当加密，以便能够较精确的模拟壁面附近的流动.整个网格分布及翼型尾部网格放大见图2.在后缘处由于考虑强度和稳定性方面问题时，经常处理为随边厚度不为0.法;离散得到的代数方程使用Gauss-Seidel迭代求解.

图2 网格划分示意Fig.2 Computational grid domain of airfoil

2.2 二维翼型气动性能算例分析

NACA64-618翼型是目前较为成熟的一种翼型，本文对该翼型在攻角范围－180°～180°的气动性能进行了分析，并与试验结果［7］进行了比较，如图3所示.相关计算参数为:变桨转矩中心位于0.25倍弦长处;雷诺数为3.0×106;计算条件取标准空气密度1.225 g/m3，空气运动粘性系数取1.789 4×10－5.

图3 NACA64-618翼型在－180°～180°的气动特性曲线Fig.3 Aerodynamic performance of airfoil NACA64-618 at attack angle－180°～180°

2.1.3 求解区域和边界条件

整个计算域为进流段和去流段都为10倍弦长，而侧面为6倍弦长，具体为10L×6L×10L，其中L为弦长.边界条件为:

1)进口边界条件:其速度等于来流速度，即V=V∞;

2)出口边界条件:压力出口，假定压力等于大气压;

3)外场边界:外场边界的设置与进口边界条件一致;

4)物面条件:叶片表面设定为无滑移边界条件，即V=0.

2.1.4 数值计算方法

二维翼型气动性能分析通过直接求解二维粘性不可压RANS方程，微分方程的离散使用有限体积法，其中对流项采用二阶迎风差分格式，扩散项采用中心差分格式;压力和速度耦合采用的SIMPLE方

由于试验［7］只给出了小攻角范围内的有关升力系数、阻力系数和俯仰力矩系数.从图3可以发现，当攻角较小时，翼型的升力系数随着攻角的增大而增大;攻角为14°时翼型的升力系数达到最大值，随着攻角继续增加，翼型的升力系数开始下降，而阻力系数则急剧上升，翼型的气动性能开始恶化.NACA64-618翼型在雷诺数为3.0×106时的失速攻角应该在14°附近，理论结果与试验结果吻合.分析大攻角下理论计算结果可以发现，此时的气动性能呈非定常特性.实际应用时，需要将有关气动性能在攻角度范围－180°～180°进行光顺处理，再导入GHBladed或Focus等风机分析软件应用.阻力系数和俯仰力矩系数基本对称，存在的差异主要由于翼型有拱度，不是完全对称剖面.

3 三维叶轮气动性能分析

二维方法可以较快捷的计算翼型的气动性能，但是该方法无法考虑叶片的三维效应，尤其当攻角达到或超过失速攻角时，叶片表面失速旋涡具有极强的三维性，采用三维方法可以更真实地模拟流场，获得风机的气动性能.

3.1 三维叶轮气动性能分析参数设置

3.1.1 计算区域和网格划分

整体计算域圆柱体区域，见图4.进口在风机前3.1D，出口在风机后5.168D，圆柱半径3.1D，其中为风轮直径.长度方向为X方向，向下游为正，Y方向为叶片参考线方向，半径朝外方向为正，Z方向满足右手法则.坐标原点在风轮的旋转中心，风轮截面垂直于X轴，迎着来流.

计算区域整体上被分为2个子区，包围叶轮的圆饼型旋转区域和其他部分的静止区域.在静止区域主要以结构化网格进行剖分.对于旋转区域网格形式以非结构网格为主，在叶片根部、梢部及导随边进行了网格加密.

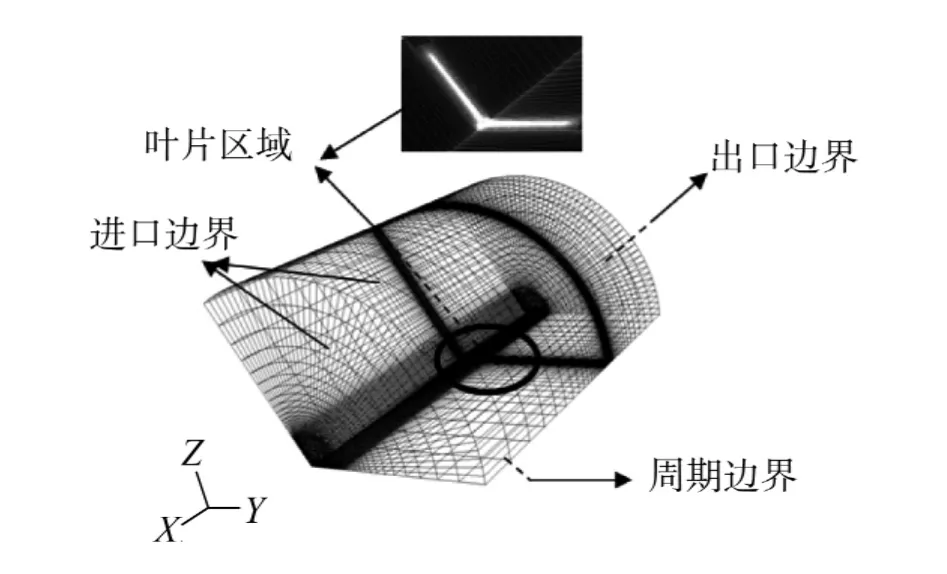
图4 计算区域外围网格示意Fig.4 Computational grid domain of wind turbine blade

3.1.2 边界条件和初始条件

计算区域的进口为速度进口边界条件，速度值设为来流风速.在计算域的上边界也同样设为进口速度边界条件.在计算域的出口为压力出口边界条件，压力值设为环境压力.计算区域的两个侧面设为周期边界条件.叶片和轮毂表面设为不可滑移物面边界.这里不考虑地面的边界层效应，所以地面设为滑移物面边界.计算初始值全域使用统一的来流风速.

3.1.3 数值计算方法

控制方程采用有限体积法进行离散，离散过程为在网格单元上对控制方程实施积分从而得到离散的代数方程组.这种离散方法可以保证控制方程的守恒性，具有较高的离散精度，可以方便地处理复杂几何问题.在离散的过程中对流项使用二阶迎风格式，扩散项采用二阶中心格式，时间项采用一阶隐式格式，对于压强和速度的耦合采用SIMPLE算法.离散代数方程采用逐点Gauss-Seidel迭代法求解，并且采用代数多重网格方法加快求解的收敛速度.

3.2 三维叶轮气动性能算例分析

3.2.1 对象描述

2MW风机叶轮的几何参数、运行参数等相关说明见表1.叶根到叶梢的翼型剖面轮廓线和三维几何造型见图5.

表1 2MW风机特性描述Table1 Description of 2MW wind turbine characteristics

图5 叶片的几何建模Fig.5 Geometrical modeling of wind turbine blade

3.2.2 计算结果与分析

基于三维方法，建立了2MW风机叶轮的气动性能分析模型，对额定风速下的流场及叶片气动性能进行了分析.

图6为叶片的压力分布云图，可以发现:

1)叶片迎风面所受风压为正压(压力面)，而背风面基本处于负压(吸力面).由伯努利效应得知:流速越快，压力越低;流速越慢，压力越高.因而叶片背风面风速大于迎风面风速.叶片迎风面压强高于大气压产生压力，背风面压强低于大气压产生吸力，由此对翼型产生升力，这也是叶片能够旋转的原因.

2)叶片迎风面，沿着翼型曲线前缘至后缘，压力变化平缓，而背风面压力变化迅速.产生这种分布的原因是翼型截面曲率导致的，当来流流经翼型表面时，翼型几何特性引起了翼型表面来流风速的变化，因而造成了压力分布的相应变化.

图6 叶片压力分布云图Fig.6 Pressure distribution on turbine blade

图7为叶表面的速度矢量图，可以观察到翼型绕流现象，且背风面风速大于迎风面风速.

图7 叶片速度矢量图Fig.7 velocity vector distributions on turbine blade

图8为叶尖速比－风能利用系数特性，与GHBladed软件计算结果比较可以发现:两者计算结果较为接近，趋势一致，但理论值略小.这是由于本文CFD计算采用粘流RANS方程，而GHBladed软件基于叶素理论，因此在旋转方向的阻力分量的理论计算较软件大，得到转矩比软件小，因此CFD计算得到的叶片吸收功率比GHBladed计算值要小.图9为叶尖速比－推力系数特性，理论计算结果与软件计算结果相当，理论值略小，这是由于推力分量中，升力贡献占主要部分，阻力分量的差异导致软件计算结果的偏大.

图8 叶尖速比-风能利用系数特性Fig.8 Characteristics of TSR-Cp

为了减小尾流的诱导损失，风叶片环量的设计分布一般采用叶根和叶梢卸载，将载荷尽力均分到叶片中间区域［8］.图10为2 MW风机的叶片环量无因次化后的径向分布，它反映了叶片径向载荷的变化趋势，叶片载荷最大位置在0.4R处.从图中可以发现，2 MW风机叶片的环量分布还是比较合理的.为了将其径向环量更均匀地分布到叶片中间区域，作者调整了叶片中间区域的弦长和扭曲角，使叶片环量在中间分布得更均匀，计算结果表明优化方案在设计尖速比附近的Cp比原型提高了3%左右.

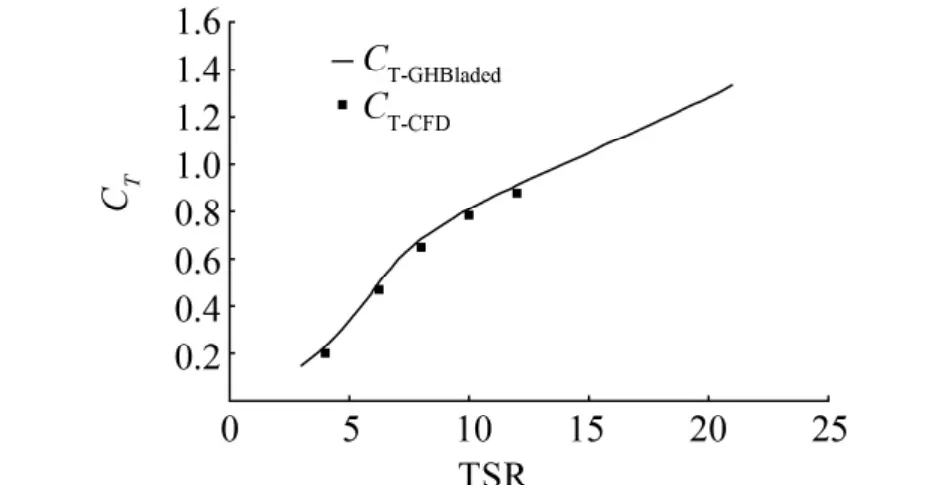
图9 叶尖速比-推力系数特性图Fig.9 Characteristics of TSR～CT

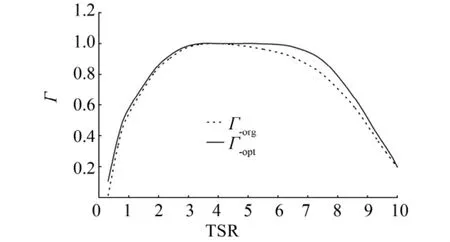
图10 叶片环量无因次化后的径向分布Fig.10 Distribution of circulation along radii of wind turbine blade

4 结论

本文基于CFD技术，建立了大型风力发电机组叶片气动性能分析方法，通过算例分析与比较，得到了以下结论:

1)小攻角下的二维气动性能分析与试验结果吻合良好，大攻角下的气动性能计算结果趋势合理，证明本文建立的二维翼型气动性能分析方法是可行的，可为风机分析软件提供重要的气动输入数据;

2)2MW风机叶轮的三维气动性能计算结果与GHBladed软件吻合良好，证明本文建立的三维翼型气动性能分析方法也是可行的.压力分布与速度矢量分布显示三维方法可以更真实地模拟流场，考虑叶片的三维效应.对2MW风机叶片翼型的优化，进一步体现了三维方法的优势.

因此，基于CFD技术，采用RANS方程耦合SST湍流模型，预报二维和三维翼型的气动性能是可行的.本文研究成果对于大型风力发电机组叶片气动性能的设计与优化具有一定的参考价值.

［1］刘万馄，张志英，李银凤.风能与风力发电技术［M］.北京:化学工业出版社，2006:1-24.

［2］SORENSEN N，MICHELSEN J.Aerodynamic predictions for the unsteady aerodynamics experiment phase II rotor at the national renewable energy laboratory［EB/OL］.［1999-01-11］.http://rotorcraft.arc.nasa.gov/publications/files/ S?rensen_AIAA1999.pdf.

［3］SORENSEN N，MICHELSEN J，SCHRECK S.Navier-Stokes predictions of the NREL phase VI rotor in the NASA Ames 80-by-120 wind tunnel［C］//ASME 2002 Wind Energy Symposium.Reno，USA，2002:94-105.

［4］李仁年，李银然，王秀勇，等.风力机翼型的气动模型及数值计算［J］.兰州理工大学学报，2010，36(3):65-68.

LI Rennian，LI Yinran，WANG Xiuyong，et al.Aerodynamic model of airfoil for wind turbine and its numeric computation［J］.Journal of Lanzhou University of Technology，2010，36 (3):65-68.

［5］MADSEN H，SORENSEN N，SCHRECK S.Yaw aerodynamics analyzed with three codes in comparison with experiment［C］//ASME 2003 Wind Energy Symposium.Reno，USA，2003:94-103.

［6］MENTER F R.Multiscale model for turbulent flows［C］// AIAA 24th Fluid Dynamics Conference.American Institute of Aeronautics and Astronautics.Orlando，USA，1993:1-21.

［7］ABBOTT I H，VON DOENHOFF A E.Theory of wing sections［M］.New York:Dover Publications，INC.，1959: 428-430.

［8］TONY B.风能技术［M］.北京:科学出版社，2007:74-76.