声在随机介质波导中的传播
2012-04-13杨士莪
杨士莪
(哈尔滨工程大学 水声工程学院,黑龙江 哈尔滨 150001)
迄今为止,对于声在随机介质中传播起伏问题的研究,绝大部分仅限于无限介质的环境条件,很少有人讨论波导传播所可能附加的效应.而且除Rytov方法以外,所利用的数学工具,如Feynman所提出的路径积分等方法,多数工程技术人员也都很不熟悉[1-3].为此,采用逐次近似方法讨论在波导条件下,声传播起伏的某些特点,将是有实际参考意义的.为了数学上的简便,文中将仅限于讨论点源声波在具有绝对软上边界,和半无限流体介质下边界的平面平行波导中的传播,且波导和下半空间中的介质总体均匀,其平均声速和密度分别为:c0、ρ0、c1、 ρ1,但上、下方介质中均具有随机的微弱不均匀起伏,这样将仍能反映出介质起伏对声信号传播的主要影响规律.
1 声场基本方程式
取直角坐标,令波导深度为H,声源位于z轴上深度为zs处,这时波导中及下方介质中声场势函数φ(0)(r)、φ(1)(r)应满足的微分方程式可分别写为




式中,Zn(z,x,y)为第n阶局地简正波,并应满足下列方程式与边界条件:

将Zn写为ε的幂级数,即

将此表示代入式(4),按照ε的同幂次项进行整理后,可分别得到:

上述公式及今后为了书写简便起见,对φ、ψ、Z等函数,当其有关公式基本相同时,即省略各函数的肩标,而不再分别列出.已知对两层均匀介质的Pekeris波导有:


根据式(12)、(13)求解声场的一次近似时,可选用以下函数做为微分方程的2个线性独立解:

依照二阶微分方程求特解的方法,最后可得

其中:

Λn、Δn均为与随机量无关的确定性函数.由于原所选取的G1、G2均满足边界条件(11),故可知上式给出的Zn1的解,也必然满足给定的边界条件.按照以上方法,可依次求得更高阶的近似,可以看出,Zn的各高阶近似,将相应的含有μ(x,y,x)的高幂次项.为简便,在此将仅考虑Zn的一阶近似.
2 信号起伏的时空相关函数
首先计算各ψn的近似值.根据耦合简正波方法,利用各阶简正波的正交性,忽略局地简正波空间变化的二阶小量,可得:


对于不存在随机不均匀体的两层液态介质波导来说,作为0阶近似有其中并满足上式右端为0的微分方程式.注意到,故上式等号右边的项可视为当波导中存在随机不均匀体时,引发声场水平势函数分量修正值的二次声源.同样将ψn展开写成ε的幂级数:

若仅考虑一阶近似,可得:
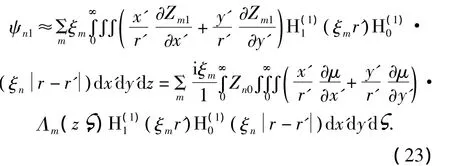
若需要计算ψn的更高阶近似,可依前述利用逐次近似法进行.当仅考虑一阶近似时,可得到波导中信号起伏值为

从上式中可以看出,由于波导中存在随机起伏的不均匀体,不仅各阶局地简正波有变化,且各阶势函数水平分量也有变化.需要注意的是:这时ψn与Zn均不是μ(x,y,z)的线性函数,因此即μ(x,y,z)服从0均值的Gauss分布规律,波导中信号起伏一般也不遵从Gauss规律,仅在一级近似条件下,可以近似的认为服从Gauss规律.
利用式(15)计算信号起伏的水平和垂直相关函数时,考虑到各不同阶简正波相互干涉,其空间平均值近似为0,因而可以仅计算相同阶简正波的结果;同时还可以考虑到,声场势函数水平分量的起伏,和介质起伏的空间梯度有关,而简正波的起伏则与介质起伏直接相关,因而可认为ψn1与Zn1相互独立,其统计平均值也可以忽略.从而得到如下公式:

设介质起伏的空间相关函数为

经过若干计算后可得:
1)波导中信号起伏的均方值:

2)波导中信号起伏的垂向相关系数:

3)波导中信号起伏的纵向相关系数:

4)波导中信号起伏的横向相关系数:

其中:

从上述各表达式可以看出,无论是波导中信号起伏的均方值,抑或是信号起伏的各项空间相关函数,都将和接收点与声源的相对位置有关.由于具体公式的复杂性,很难直接从解析公式中看出应有的规律,而需要利用数值计算进行分析讨论.由于篇幅的限制,具体的仿真计算结果,以及试验验证情况,将在后续文章中给出.
3 结论
文中介绍了一种利用逐次近似法,分析当介质环境存在微小扰动时,声在波导中远距离传播情况下的起伏方法.从有关计算过程中可以看出,由于波导中存在随机起伏的不均匀体,在声波传播过程中,不仅各阶局地简正波有变化,且各阶势函数水平分量也有变化.需要注意的是:这时ψn与Zn均不是μ(x,y,z)的线性函数,因此即或μ(x,y,z)服从0均值的Gauss分布规律,波导中信号起伏一般也不遵从Gauss规律,仅在介质起伏率甚小的一级近似条件下,可以近似的认为服从Gauss规律.随着传播距离的竲加,高阶简正波逐渐衰减,信号起伏的空间相关将会逐渐竲大,但具体的规律十分复杂,将在后继工作中借助数值分析进行讨论.
[1]YANG Shie.Theory of underwater sound propagation[M].哈尔滨:哈尔滨工程大学出版社,2009.
[2]FLATTE S M.Sound transmission through a fluctuating ocean[M].Cambridge:Cambridge University Press,1979.
[3]Ярощук И О,Гулин О Э.Метод статистичекого моделирования в зачах гидроакутики.Владивосток Дальнаука,2002.
[4]BERTSATOS I.General second-order covariance of Gaussian maximum likelihood estimates applied to passive source localization in fluctuating waveguides[J].The Journal of Acoustical Society of America.2010,128(5):2635-2651.
