广义α算法在拖曳阵列动态仿真中的应用

张广磊，张维竞，刘涛

(上海交通大学 海洋工程国家重点实验室，上海 200240)

水下拖缆系统在海洋上有着广泛的应用:军事上，海军利用水面拖曳阵列声呐系统来执行勘探及反潜任务;民用上，海上资源勘探拖缆系统是目前世界上进行海洋油气资源勘探的主要手段.拖曳阵列系统通常由拖船(或军舰)、引导拖缆(重力缆)、零浮力拖缆阵列、水下拖体及各种缆载探测控制设备等组成.拖缆作为整个拖曳系统的重要组成部分，而我国在海洋拖缆系统方面的研究起步较晚，技术上明显落后于美国等发达国家［1］，对于拖缆动力学方程求解方法的研究相对较少.基于二阶精度的有限差分Box method［2-3］是目前拖缆方程求解最普遍适用的方法，它把拖缆的控制方程在时间和空间上采用半网格点方法离散，自从Ablow和Schechter［4］首次采用它来求解拖缆的方程以来，由于它具有精度高和易实现的特点，相继被Park、Ioannis、HUO Cunfeng和Mark等［5-8］很多研究人员采用，但该方法在时间上离散求解存在着稳定性较差的缺点，Koh等［9］在其论文中证明了有限差分Box method时域上稳定性差的缺点，在空间上对变量离散保留了Box method的方法，而时间上提出采用向后差分的方法避免了时间上离散求解的不稳定性，然而这种方法时间上只有一阶精度.Sun等［10］在时间上采用广义梯形方法来优化求解的稳定性，具有一定的数值耗散［11］性，但这种方法只有在其数值耗散性能最差的时候才具有二阶精度.Gobat等［2-3，12］提出了具有二阶精度的广义α算法，并将之应用到二维拖缆的求解过程中.

本人在前人研究的基础上，对三维拖缆非线性动态方程在时间域上采用广义α算法离散，分析证明了该方法求解拖缆方程在时间上具有二阶精度，将该方法应用到三维拖缆方程的求解，并通过将该方法与几种常用的方法进行仿真实验对比，分析了其求解的稳定性及精确性.

1 拖缆的控制方程

采用Ablow所建立的模型，假设拖缆为圆柱型刚性缆，忽略拖缆弯曲应力［13］和海流的影响得到的方程如下:

式中:s为未伸长缆单位长度，t为时间变量，m为单位长度未伸长缆的质量，m1为缆的附加质量与缆的质量的和，A为未伸长缆的截面积，E为弹性模量，ρ为水的密度，ω0为单位长度缆在水中的重量，θ、φ为欧拉角度，V(Vt，Vn，Vb)局部坐标中的速度矢量，Rd(Rd1，Rd2，Rd3)为水动力.

定义Y(s，t)=(T，Vt，Vn，Vb，θ，φ)，因此方程(1)～(6)写成矩阵的形式为

2 拖缆方程的离散

2.1 空间的离散

这里拖缆方程在空间上的离散采用Ablow和Schechter所用的基于二阶精度的有限差分 Box method方法，假设把缆划分为n个节点，那么拖缆的动态方程就可以离散为n－1个矩阵方程:

2.2 时间的离散

2.2.1 广义α算法

在时间上的离散采用广义 α算法，Gobat和 Grosenbaugh［11］证明了有限差分Box method在时间离散上存在着求解的不稳定性，并把广义α算法应用到二维拖缆的求解问题.广义α算法在时间上离散形式为

其中，

式中:Δt表示时间步长，αm、αk和γ则构成了广义α算法.

为了比较方便的证明广义α算法的精度及稳定性，考虑单一自由度问题，则有

其中，ω为频率，式(16)即为下列方程的差分形式:

假设y(ti)是常微分方程(17)的一个精确解，那么截断误差可以定义为

其中，Bn、Cn为式(16)中yi和fi的系数，将yi、fi用泰勒级数展开，并代入式(17)经过运算化简可得

可以看出当αm－αk+γ=0.5时，广义α算法具有二阶精度.为了便于讨论广义α算法的稳定性，将广义α算法写成增广矩阵的形式:

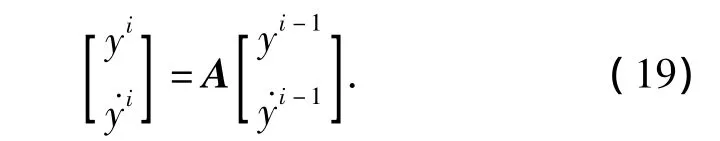
式中增广矩阵定义为

下面，通过分析矩阵的特征值λ1，2以及谱半径ρ来检测算法的数值耗散性能，增广矩阵的谱半径定义为

假设当ωΔt→∞增广矩阵的特征值λ1，2为2个相等的实数值，那么式(21)就可以化为只含有1个参数的方程，定义λ∞为ωΔt∞时矩阵的双重特征值，则αm、αk和γ可由以下方程来计算:

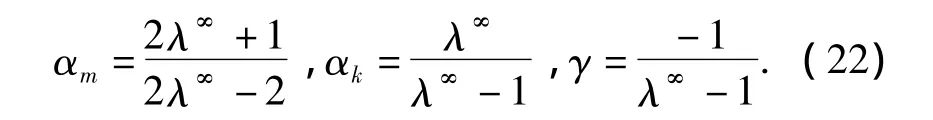
由以上广义算法的形式可知，有限差分 Box method、广义梯形法以及向后差分法都是广义α算法的特殊形式，只是αm、αk和γ的取值不同而已，表1给出了几个不同算法αm、αk和γ的值.

表1 广义α算法的几种特例Table 1 Several special cases for generalized-α algorithm

图1 广义α算法及其几种特例的谱半径Fig.1 The spectral radius of generalized-α algorithm and several special cases

图1所示为表1内的几种广义α算法的谱半径图，从图中可知，有限差分Box method(λ∞=－1.0)就像一个全通滤波器，它没有任何的数值耗散.向后差分算法子在较高频段衰减曲线虽然比较光滑，但是这种算法只具有一阶精度.当λ∞=0.0时广义α算法具有二阶精度，但是其谱半径图上有个拐点，这说明增广矩阵的一个特征值从拐点开始转变成2个共轭的特征值，与假设不符.广义梯形法对中低频滤波效果明显，然而在较高的频率段，梯形法则几乎没有数值耗散.Gobat等［2-3，12］经过仿真研究对比发现，对于大多数拖缆问题，当λ∞在［－0.3，－0.7］取值时，虽然增广矩阵具有2个不相等的实特征值，但其谱半径随着频率的增加逐渐减小，或者仅有微小的增加，具有较好的稳定性.这里在仿真计算时取λ∞=－0.5，其谱半径见图1所示.

2.2.2 广义α算法求解非线性问题

广义α算法在求解线性问题时，由于系数矩阵M、K是不变的，所以可以用式(12)进行计算，但是对于非线性问题系数矩阵则随时间的变化而改变，那么算法的稳定性将随时间有条件收敛.

为了避免这个问题，提高算法的稳定性，系数矩阵必须取固定值，普遍采用相同权重的方法来计算平均系数矩阵，其是用速度和位移矢量的平均值来计算.广义α算法矩阵M和矩阵K的系数分别用αm、αk表示，这样算法的表达形式为

3 数值仿真及对比分析

3.1 边界条件

1)拖缆首端边界条件:

首端缆上拖点的速度与拖船速度相同，即

式中:Vx、Vy、Vz为拖船航速在固定坐标系X、Y、Z方向上的速度分量.

2)尾端自由端边界条件:

自由端张力为零，即T=0.

3.2 数值仿真及对比分析

为了分析广义α算法的精度和稳定性，这里仅考虑回转运动情况.计算的状态为:首先拖船沿某一固定方向以18.5 kn的速度直线运动1 s，然后进入半径为0.64 km的回转运动440 s，最后，在完成375°的回转后，沿圆周的切线直线运动300 s.在计算时，所用的时间步长和整个系统的分段数均与文献［4］相同.这里参数设定部分参考文献［4］，表2如下.

表2 拖缆阵列参数Table 2 Towed array parameters

图2 几种常用方法计算结果Fig.2 Calculation results of several commonly used methods

图2给出了可用广义α算法表示的几种算法计算拖缆回转运动的结果图，利用表3对仿真结果进行对比分析比较，其中Rispin的数据为实验数据，来自于文献［4］.考虑到实验的误差、海流、船舶等的影响，广义α算法和差分Box method结果基本和实验相符，而向后差分、广义梯形法由于算法精度的影响与实验有少许的偏差.

表3 实验与几种计算方法结果的比较Table 3 Comparison of experimental and numerical resultsm

为了说明算法收敛性的优越，图3给出了几种算法计算拖缆回转运动的每一点的平均误差图，表4记录了各种算法的运算时间，这里空间步长取2 m，时间步长与文献［4］相同均为20 s，仿真总时间为37 s，所用的计算机参数为:CPU为 Inter Pentium Dual E2160主频为1.79 Hz，内存为1.99 GB.仿真实验分析表明，广义α算法、向后差分以及广义梯形法比差分Box method具有较好的收敛性，因此计算它们的计算时间相对于差分Box method有很大的优势.

表4 几种方法的运算时间比较Table 4 Operation time of several methods

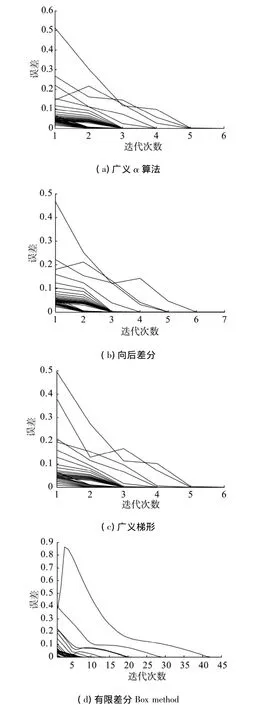
图3 几种计算收敛性图Fig.3 Convergence of several methods

通过以上对广义α算法、向后差分、广义梯形和有限差分Box method仿真计算对比分析研究，可以发现广义α算法具有收敛效果好，计算时间短，计算精度高等优点，为求解非线性拖缆方程提供了一个较好的解决方法.

4 结束语

本文通过数学运算证明了广义α算法具有二阶精度，对比分析了有限差分Box method、广义梯形算法，向后差分算法以及不同的值广义α算法的稳定性和精确性，研究表明，在－0.3到－0.7之间取值时，广义α算法对拖曳阵列有较好的求解稳定性.将广义α算法用于拖缆的非线性动态方程求解，在空间上保留有限差分Box method的变量离散的方法，在时间上采用广义α算法变量离散方法，并与向后差分、广义梯形和有限差分Box method进行对比仿真实验，仿真结果表明，广义α算法不仅有较好的求解准确性，而且有较短的仿真运算求解时间，为提高我国拖曳阵列的控制技术提供了一个较好的解决途径.

［1］张维竞，张小卿，陈峻.基于嵌入式水鸟的海洋地震拖缆运动状态仿真研究［J］.海洋工程，2009，27(4):81-86.

ZHANG Weijing，ZHANG Xiaoqing，CHEN Jun.Simulation study on the movement states of marine seismic streamer based on embedded birds［J］.The Ocean Engineering，2009，27(4):81-86.

［2］GOBAT J I，GROSENBAUGH M A.Applications of the generalized-α method to the time integration of the cable dynamics equations［J］.Computer Methods in Applied Mechanics and Engineering，2001，190(6):4817-4829.

［3］GOBAT J I，GROSENBAUGH M A.Dynamics in the touchdown region of catenary moorings［J］.International Journal of Offshore and Polar Engineering，2001，11(1): 273-281.

［4］ABLOW C M，SCHECHTER S.Numerical simulation of undersea cable dynamics［J］.Ocean Engineering，1983，10 (6):443-457.

［5］PARK H I，JUNG D H，KOTERAYAMA W.A numerical and experimental study on dynamics of a towed low tension cable［J］.Applied Ocean Research，2003，25(10):289-299.

［6］HUO Cunfeng，YAO Baoheng，FU Bin，et al.Investigation on transient dynamic behaviors of low-tension undersea cables［J］.Journal of Shanghai Jiaotong University，2011，16 (1):34-39.

［7］CHATJIGEORGIOU I K.3 dimensional nonlinear dynamics of submerged，extensible catenary pipes conveying fluid and subjected to end-imposed excitations［J］.International Journal of Non-Linear Mechanics，2010，45(4):667-680.

［8］GROSENBAUGH M A.Transient behavior of towed cable systems during ship turning maneuvers［J］.Ocean Engineering，2007，34(8):1532-1542.

［9］KOH C G，ZHANG Y，QUEK S T.Low-tension cable dynamics:numerical and experimental studies［J］.Journal of Engineering Mechanics，1999，125(3):347-354.

［10］SUN Y，LEONARD J W，CHIOU R B.Simulation of unsteady oceanic cable deployment by direct integration with suppression［J］.Ocean Engineering，1994，21(6):243-256.

［11］马秀腾，陈立平，张云清.约束力学系统运动方程积分的数值耗散研究［J］.系统仿真学报，2009，21(20): 6373-6377.

MA Xiuteng，CHEN Liping，ZHANG Yunqing.Research on numerical dissipation of integration methods for motion equations in constrained mechanical systems［J］.Journal of System Simulation，2009，20:6373-6377.

［12］GOBAT J I，GROSENBAUGH M A.Time-domain numerical simulation of ocean cable structures［J］.Ocean Engineering，2006，33(10):1373-1400.

［13］王飞，陈锦标，涂兴华.低速低应力时拖揽运动仿真［J］.上海交通大学学报，2010，44(6):828-832.

WANG Fei，CHEN Jingbiao，TU Xinghua.Numerical simulation of towed low-tension cable［J］.Journal of Shanghai Jiaotong University，2010，44(6):828-832.