基于ABAQUS的龙门框架振动特性分析

2012-04-10杨旭东李家春

制造业自动化 2012年16期

杨旭东，孙栋，裔黔，李家春

YANG Xu-dong1,SUN Dong1,YI Qian2,LI Jia-chun1

（1. 贵州大学机械工程学院，贵阳 550018；2. 贵航东方机床有限公司，都匀 558000）

0 引言

由于大型龙门机床框架内部结构和受力情况复杂，采用常规手工算法和现场测试耗时耗力，且很难得到精确的结果，无法直观了解振型。ABAQUS作为一款功能强大的有限元分析软件，能够高效准确地进行结构动力学分析，自动提取各阶固有频率并动态显示相应振型，极大缩短产品设计周期。

1 结构分析

该型号龙门刨床主要用于加工平面、斜面、沟槽和成形表面，工作台面宽度2000mm，长度6000mm。左右立柱和连接梁组成封闭式龙门框架，具有较高的刚度和抗振性。其中立柱为薄壁箱型结构，内部布置筋板以增加其刚度。首先运用Solidworks分别建立左右立柱和连接梁的三维建模，然后进行装配，所得龙门框架模型如图1所示。

2 动力学分析理论

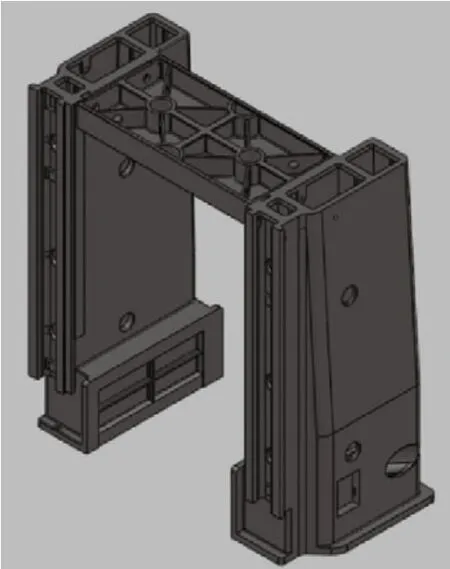
图1 龙门框架三维模型

动力学分析是用来确定惯量和阻尼起重要作用时结构或构件动力学行为的分析技术，常见的动力学行为包括振动特性、载荷随时间变化的效应、周期载荷激励等。其中，振动特性即模态，每一个模态具有特定的固有频率、阻尼比和模态振型。这些模态参数可以由计算或试验分析取得，这样一个计算或试验分析过程称为模态分析。

固有频率可以通过分析结构在无载荷时的动态响应而得到。当外力为零时，运动动力学平衡方程为：

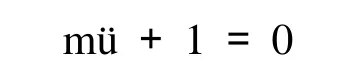
式中，m是结构的质量； ü是结构的加速度；I是结构中的内力。在无阻尼系统中，I=Ku，则上式变为：

这个方程解的形式为：

将此式代入运动方程中便得到特征值问题方程：

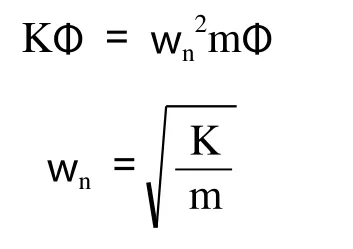
该系统具有n个特征值，此处n是有限元模型的自由度数，ωj即为结构的第j阶固有频率，φj是相应的特征向量。特征向量也就是所谓的模态。

机床在以一定频率变化的正弦交变载荷（激振力）作用下，所表现的刚度称为动刚度，它是衡量机床抗振性的主要指标，其数值等于产生单位振幅所需的动态力

又过了一年，双方父母都在催办婚事。蒋海峰想明白了，已经躲不过去，把结婚证领了。结婚后，蒋海峰不回家。紫云困守着租来的窄屋，冷冷清清。

式中，KD为动刚度，F为动态力，A为振幅。

一般说来，动刚度是频率的函数，而且对于不同类型的振动，其数值是不同的，动刚度越大，表示机床的动态力的作用下振幅越小。机床的动刚度取决于机床振动系统动态特性参数：

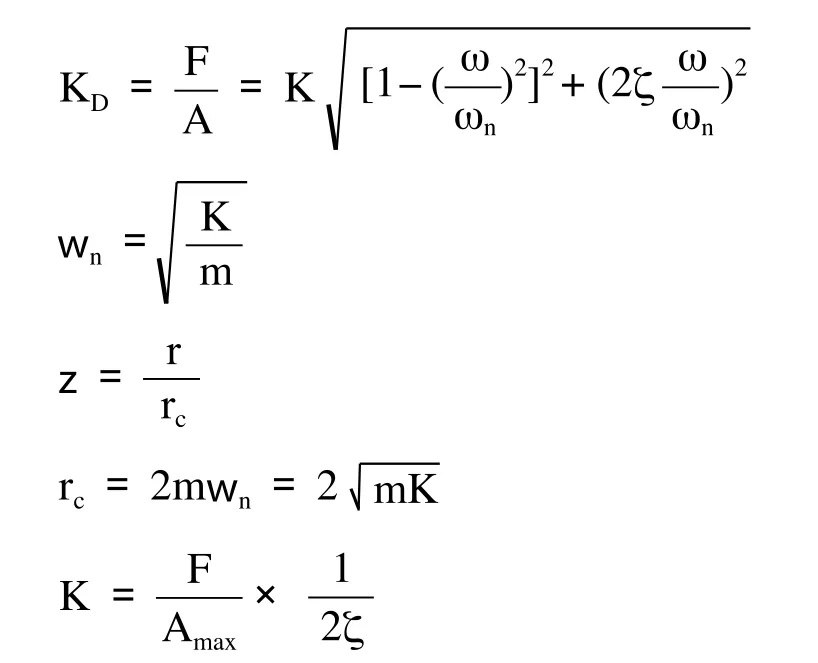
式中，ωn为固有频率，ω为激振频率，m为当量质量，K为当量静刚度，F为激振力，Amax为共振振幅，ζ为阻尼比，r为阻尼系数，rc为临界阻尼系数。当时，为共振状态，此时动刚度值KD最小，以Kd表示：

可见，系统的阻尼比ζ越大，当量静刚度K或固有频率ωn越高，则动刚度越好，也即抗振性越好[1,2]。机床属于多自由度振动的系统，具有多个固有频率，因此，在设计结构时避免使各固有频率与可能的载荷频率过分接近就很重要，本文就是通过模态分析进行机床刚度评估，进而找出需要改进的动态薄弱环节。

3 建立有限元模型

三维模型中的一些尖角等细小特征会增大有限元分析计算量，甚至影响网格划分而无法求解，因此为了在保证计算精度的前提下提高计算经济性，需要对原有三维模型进行适当简化。本模型中去掉了结构中较小的圆角和倒角以及对结构刚度影响不大的安装孔、安装凸台以及台阶面等。

将简化后的装配模型导入ABAQUS，单位采用T-mm-s单位制。定义材料名称HT200，密度为7.2×10-9T/mm3，弹性模量为1.48×105Mpa，泊松比为0.31。立柱脚部翻边通过地脚螺栓完全固定，侧面与床身凸耳固定，连接梁两端分别与左右立柱固定。由于龙门框架结构复杂，故采用自由网格划分方式，网格类型选用精度较高的C3D10M（修正的十节点二次四面体单元）[3]，全局网格大小设置为80，划分网格后总结点数为143842，总单元数为73941。所得模型如图2所示。

图2 龙门框架有限元模型

4 模态分析

在模态分析中，因振动被假定为自由振动，所以只有边界条件起作用，其它载荷对分析结果毫无影响。设置分析步为线性摄动步（liner perturbation）中的频率提取分析步（frequency extraction）。由于高阶模态的固有频率已远高于实际工况所能达到的激振频率，一般不会发生共振，故只提取前30阶固有频率和振型[4～6]。龙门框架前10阶固有频率参见表1。各阶振型主要是龙门框架的摆动的扭曲，前两阶振型如图3所示。