基于粒子群和16控制区的无功电压优化控制技术及其应用
2012-04-10谢开贵
唐 锋,谢开贵,徐 锐,杜 峰
TANG Feng,XIE Kai-gui,XU Rui,DU Feng
(重庆大学 输配电设备及系统安全与新技术国家重点实验室,重庆 400044)
0 引言
电压作为电力系统考察电能质量的指标之一,其主要反映电网中的无功平衡。电压波动过大对系统的稳定和安全运行产生极大影响,甚至引起系统电压崩溃,造成大面积停电事故[1,2]。因此,无功平衡及电压稳定对电力系统至关重要。
国外于上世纪七十年代末开始开发及应用基于全网分层分区的AVC系统[2,3]。应用三层控制结构设计,实现了对电压无功综合控制。这种方法虽然简单,但缺点为其经济及技术效益相对较低,并且难以完全实现全范围的电压无功最优控制[4]。
我国电网主要采用分散方式实现电网的电压无功综合控制[5~8],即在各变电站利用现有无功调节手段来实现电压无功综合控制,根据系统电压与功率因数的九区图来调节变压器分接头或投切电容器组,来实现系统的电压无功功率控制。这种方法虽然一定程度上改善了主变低压侧电压,但这种方法的控制判决对系统电压及功率因数的综合识别能力考虑存在缺陷,因此会导致变压器分接头、电容器组的频繁调节和投切。
本文对电力系统无功电压综合控制的各种策略进行了研究,对电力系统无功电压综合控制的不同模式进行分析,针对当前电压无功控制中存在的问题,提出结合改进九区域图和粒子群优化算法的地区电网电压无功控制策略。对传统粒子群算法进行了改进,建立了优化计算数学模型。该方法以全电网有功损耗最小为控制目标,最大限度地利用已有的无功设备,并考虑如何限制调节装置的动作次数,实现电压和无功的全网最优控制。并结合地区电网实时数据进行了仿真计算和分析。
1 无功电压控制的数学模型
无功电压优化控制模型是混合非线性的多变量多约束优化问题[9~11]。通过调节控制变量,如:发电机端电压、变压器分接头档位和并联电容器,从而实现无功潮流优化分布,达到提供电压质量,减少电能损耗的目的。
以系统有功网损最小和节点电压水平最合理为目标函数,将电压质量和发电机无功出力作为罚函数引入目标中形成增广的目标函数,建立数学模型,如式(1)所示:

式中,
Nb、N——系统支路数和节点数;
Npv——PV节点的个数;
λ1、λ2——越限项的罚因子;
Vi、δi——节点i电压幅值和相角;
Gk (i,j)——线路ij的电导;
Pi、Qi——节点i注入有功和无功功率;
max,min——对应变量的上限和下限值。
Vilim、Qilim如下所示:

等式约束包括潮流平衡方程,如式(2)所示:

不等式约束包括控制变量和状态变量约束。
1)控制变量约束:发电机电压幅值上下限约束、变压器分接头约束和电容器组数约束,如式(3)所示。
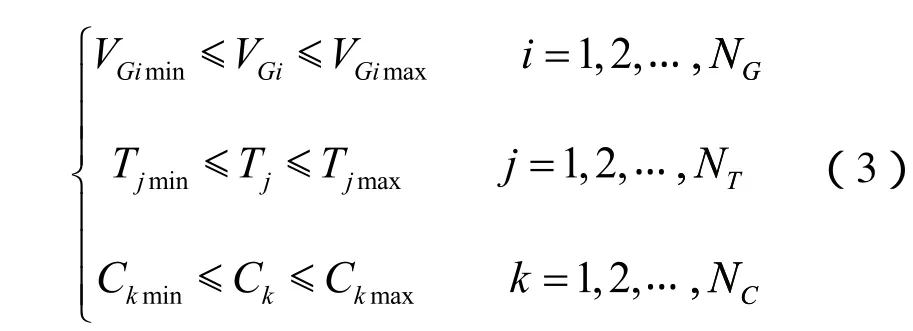
2)状态变量约束:负荷节点电压幅值约束和发电机无功出力约束,如式(4)所示。

式中:
NG——系统中发电机节点数;
NT——可调节变压器数;
NC——补偿电容器个数;
ND——负荷节点数;
VGi——第i台的发电机端电压;
TJ——第j台变压器的变比;
Ck——第k个可投切位置的电容器补偿容量;
QGj——第j台发电机的无功出力。
2 基于改进多粒子群算法的无功优化算法
本文提出的基于改进多粒子群算法的无功电压优化控制算法共分为三部分:短期(日)负荷预测、网络拓扑分析及潮流计算和无功电压优化计算。
首先读取SCADA量测数据,对网络拓扑分析的结果、控制设备(包括有载调压变压器和无功补偿设备)的状态参数以及负荷预测的结果等进行数据的预处理,将当前的负荷值与历史负荷值进行比较,得到负荷的变化趋势。与负荷预测的结果进行对比。若两者变化趋势一致,则选择与负荷预测结果相对应的控制策略;如果两者变化趋势不一致,则选择根据当前负荷波动情况制定的控制策略。通过无功优化计算,得出控制方案,经潮流计算校核后由SCADA系统执行。
无功优化计算流程如图1所示。
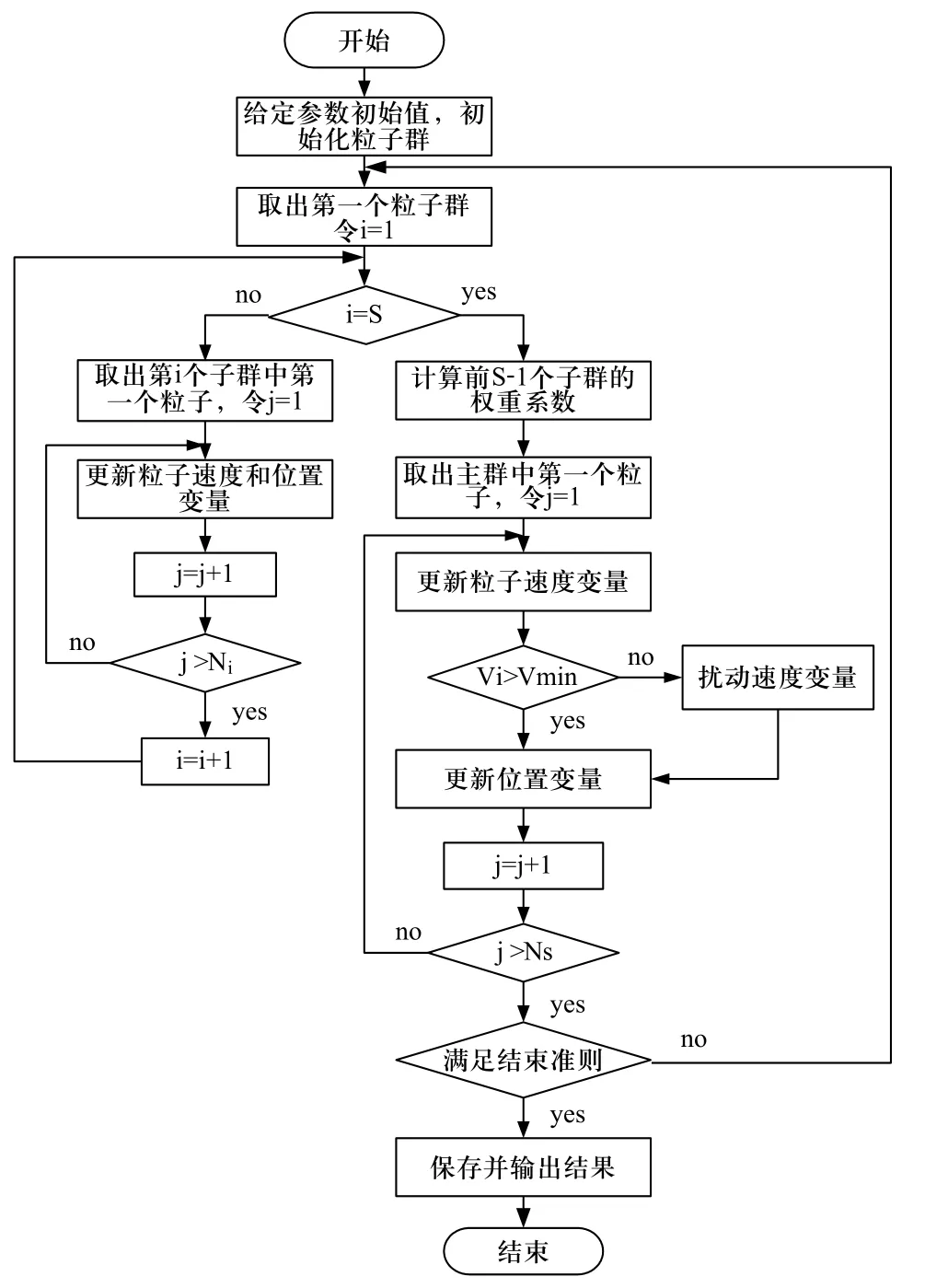
图1 无功优化计算算法流程图
结合电网运行实际情况和集控中心自动化系统现状,通常收敛判据可设置为最大迭代次数,最优解的给定值或网损减少的规定值等。
3 电压校正控制策略
本文采用“厂站级”电压校正控制策略,利用改进的九区图方法,实现电压校正控制。
基于传统的九区图原理,厂站级电压校正控制如图2所示。图中U为厂站二次侧母线的电压,cosq和Q分别为变压器高压侧绕组的功率因数和无功。按电压和无功上下限值将电压—无功平面划分为9个区域,各个区域对应不同的控制策略。
其中,cosqL、cosqH分别表示功率因数cosq上、下限;UH、UL分别表示母线电压上、下限。

图2 传统九区控制策略图
传统的九区图法存在的主要问题:控制策略没有考虑无功补偿与电压调节的相互协调关系;运算分析信息具有分散性、随机性,导致控制决策的不确定性,进而造成了变压器分接头频繁调节和电容器组频繁投切。文献[14]指出该图中处于边界附近的运行点,如A、B、C和D点,仅采用cosq或Q固定的上下限值也不能全面反映系统无功功率的大小和方向。
本文从分区划分方案、无功功率限值和控制策略三个方面对传统九区图控制策略进行了优化。
1)分区划分方案
用无功功率Q上下限替代传统九区图的功率因数cosq上下限。将区域重新细化为16区,划分原则如图3所示。
其中:
QH——无功功率Q上限;
(QH+QH) / 2——无功功率Q上下限均值;
QL——无功功率Q下限;
UH——母线电压U上限;(
UH+UL) / 2——母线电压U上下限均值;
UL——母线电压U下限。

图3 16分区控制策略图
2)QL和QH的确定
由于16区图中无功功率限值和电网运行状态有关,因此根据电网运行状态实时确定16区图中待求的Q的上下限值QL和QH。然后根据QL和QH来作为切投电容器组的依据。
无功Q小于QL时断开电容器,从两种情况考虑QL。
(1)出现无功功率过补,则断开电容器组。
(2)出现无功功率欠补,则观察断开电容器后,如果功率因数仍大于控制策略是基于固定的电压无功上下限而未考虑无功调节对电压的影响及其相互协调关系;功率因数限值则可以断开,反之则不能断开,即:
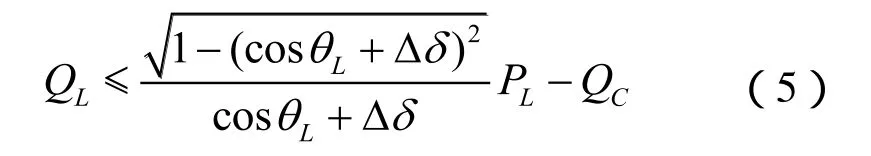
式中:
QC——电容器的额定容量;
PL——实时有功功率;
cosqL——功率因数限值;
Dd——裕度(0.025)。
当无功Q大于QH时系统投入电容器。QH按如下原则考虑。
a)保证功率因数达标,根据当前负荷有功功率和功率因数限值,按式(6)计算出无功功率上限:

b)为防止系统无功功率过补偿,根据电容器的额定容量,乘以一个系数k (0.9 c)取式(6)和式(7)最大值的作为16区图的无功量的上限。 各个区的控制规则如下: 5、6、9、10区:电压无功均合格,不调节,此4区为稳定工作区。 0区:Q 1区:QL 2区:QH>Q>(QH+ QH) / 2,U>UH。 首 先 调节分接头降低电压,若仍无法满足时,强行切除电容器。 3区:Q>QH,U>UH。首先调节分接头降低电压,再强行切除电容器。 4区:Q 7区:Q>QH,UH>U>(UH+ UL) / 2。 调 节 变压器分接头降低电压。 8区:Q 11区:Q>QH,UL 12区:Q 13区:QL 14区:QH>Q>(QH+ QH) / 2,U 15区:Q>QH,U 运用本文的数学模型和优化算法对西安东郊电网2007年6月28 日的实时运行数据进行了分析计算和控制,东郊电网正常方式运行。 计算采用的西安东郊地区电网拓扑结构如图4所示。 图4 东郊地区电网拓扑结构图 西安东郊地区电网系统总有功负荷为541.14MW。无功负荷为208.75MVAR。无功优化控制前系统网损:21.48MW,经计算和控制后,系统网损为:19.58MW。 本文将粒子群算法应用于求解东郊电网无功电压优化控制中,以实际运行的西安东郊地区电网为模型进行了在线分析计算和实际控制,初步降低了网损,提高了电压水平。结果表明,将该算法应用于该问题的求解是正确有效的,具有较稳定的收敛性能和较高的计算精度,结果证明本方案是一种科学、安全和有效的无功电压优化控制方法。 在优化过程中,考虑限制控制装置的频繁操作,通过作为约束条件转化为罚函数项控制,取得了较好的效果,使得优化结果满足实际电网运行要求。 对传统的九区域图无功控制进行研究分析,从分区划分、无功功率或功率因数的限值和控制策略三个方面进行改进,提出了一种基于规则的分区控制电压校正控制方法,实现对电网电压越限和潮流不收敛状况下电压校正控制,使其具有更广阔的应用前景。 [1] Chebbo A M,Irving M R,Sterling M J H. Reactive power dispatch incorating voltage stability [J]. IEE Proceedings C,1992,139(3): 253-260. [2] Bourgin F,Testude G,Heilbron B,et al. Present practices and trends on the French power system to prevent voltage collapse[J]. IEEE Transcations on Power System,1993,8(3): 778-788. [3] Bourgin F,Testude G,Heilbron B,et al. Present practices and trends on the French power system to prevent voltage collapse[J]. IEEE Transcations on Power System,1993,8(3): 778-788. [4] 丁晓群,周玲,陈晨,等. 无功/电压优化控制软件[J]. 中国电力,2001,34(6): 49-50. [5] 王耀瑜,张伯明. 一种基于专家知识的电力系统电压无功控制分级分布式优化控制分区方法[J]. 中国电机工程学报,1998,18(3). [6] 岑文辉,李国有,等. 应用人工神经网络进行无功电压控制[J]. 中国电机工程学报,1992,12(3). [7] 马晋涛,杨以涵,等. 遗传算法在电力系统无功优化中的应用[J]. 中国电机工程学报,1995,15(5). [8] 刘玉田,马莉. 基于 Tabu 搜索方法的电力系统无功优化[J]. 电力系统自动化,1999,23(10). [9] 吴浩忠,吴浩. 电力系统无功与电压稳定性[M]. 北京: 中国电力出版社,2004. [10] 马维新. 电力系统电压[M]. 北京: 中国电力出版社,1998. [11] 许文超,郭伟. 电力系统无功优化的模型和算法综述[J].电力系统及其自动化学报,2003,15(1): 100-104. [12] 袁亚湘,孙文俞. 最优化理论与方法[M]. 北京: 科学出版社,1997. [13] 陈宝林. 最优化理论和算法[M]. 北京: 清华大学出版社,1989 [14] 赵登福,司喆,杨靖,等. 新型变电站电压无功综合控制装置的研制[J]. 电网技术,2000,24(6): 14-17
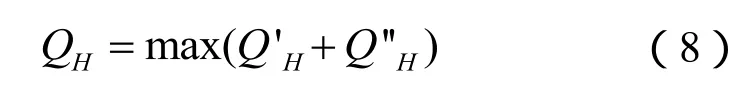
4 算例分析
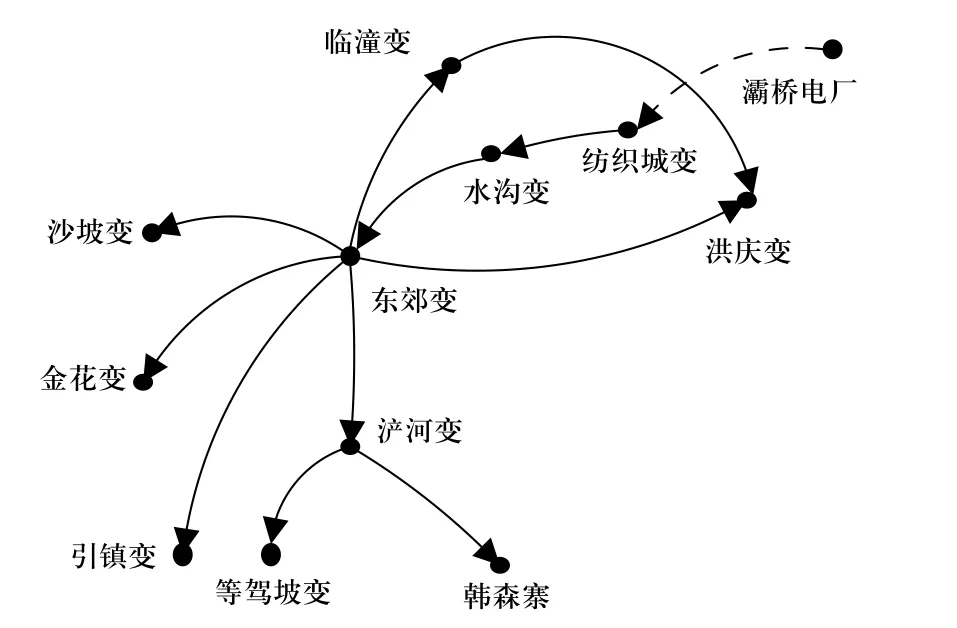
5 结论
