一种改进的扬声器Volterra模型研究

韦峻峰，冯海泓

（1.中国科学院 声学研究所东海研究站，上海 200032；2.中国科学院 声学研究所嘉兴工程中心，浙江 嘉兴 314006）

在电子消费类产品需求推动下，更轻、更薄且声音足够大成为当前扬声器的设计趋势。然而，这些设计使扬声器更多地工作在非线性区域，小信号模型已不能很好地表述其工作状态。扬声器的非线性参数辨识正成为当前研究的热点问题。Kaizer［1］最先将Volterra级数引入了扬声器的大信号建模。此后，Klippel将扬声器的小信号模型进行扩展，提出了镜像滤波器法［2］实现扬声器的大信号建模。Jeong［3］基于Volterra模型提出了谐波平衡法，简化了频域求解非线性方程的运算。

然而，在实际使用Volterra模型对扬声器进行建模时并不能很好地反映扬声器的非线性失真，模型在大幅度激励信号下输出误差显著增大。因此，一些基于扬声器Volterra模型的应用在小信号输入下的效果要优于大信号输入的结果，这些应用包括扬声器参数辨识、非线性失真补偿等［4-5］。针对这一问题，本文对动圈扬声器进行了1～3阶Volterra建模，结合扬声器大信号的工作特点，将振膜的平衡位置偏移量及高阶核函数互调响应用于模型的修正。实验表明，改进的Volterra模型在大信号激励的情况下与实验结果更为一致。

1 扬声器Volterra模型

1.1 动圈扬声器的大信号等效电路

考虑动圈扬声器在大振幅工作状态下，因定心支片、折环、磁路和音圈等部件的特性发生变化而导致回放声音中产生的失真，通常称为固有非线性失真。Klippel曾对固有非线性失真的成因、现象及模型参数进行了一系列的研究［6］。在其研究中，部分扬声器的参数不再被视为常数，而被修改为与位移、电流相关，这些参数称为大信号参数。将扬声器线性模型中的相关参数替换为大信号参数后，可以得到如图1所示的大信号等效电路。

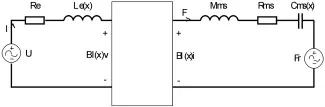
图1 动圈扬声器的大信号机械-电等效电路Fig.1 Large signal electro-mechanical analogous circuit of moving coil loudspeaker

由等效电路可建立如下微分方程：

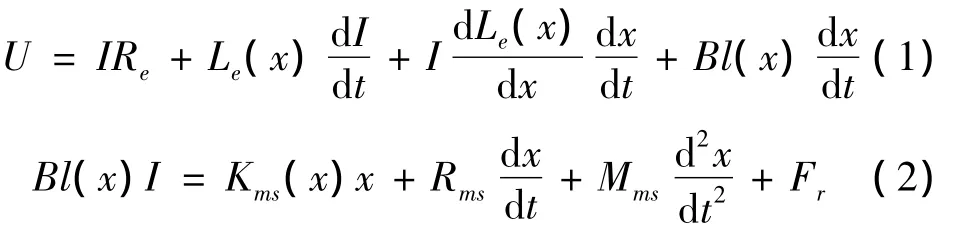
其中，Fr是电磁驱动力［6］，由随位移变化的电感产生，其表达式为：

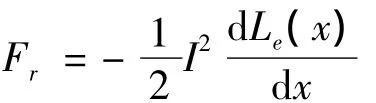
当扬声器工作在小振幅状态时，对式（1）与式（2）进行Laplace变换，可写为：

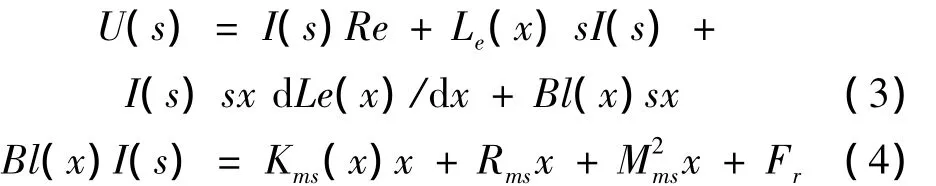
由于振膜位移x很小，Bl（x）、Le（x）和Kms（x）可视为常数，分别记为b0、l0和k0。扬声器的阻抗特性Z（s）和电压-位移传递函数Hu1（s）为：

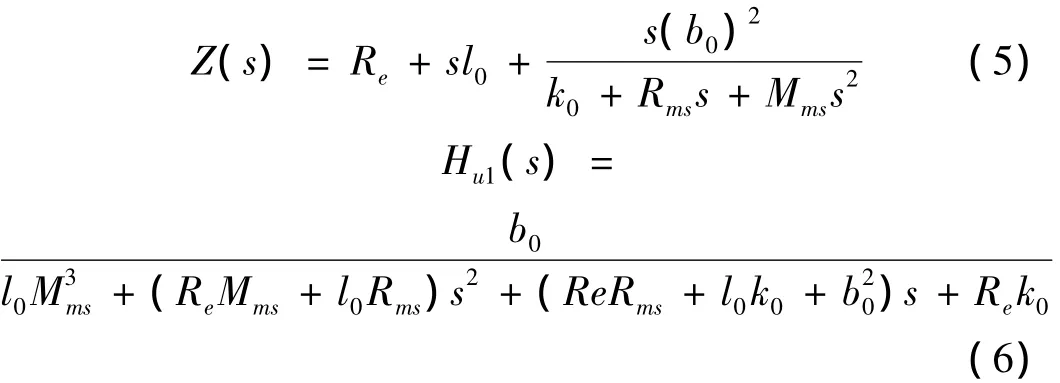
1.2 大信号Volterra模型

当扬声器工作在大振幅状态时，由于参数Bl（x）、Le（x）和Kms（x）随着振膜位移x的变化而变化，其输入与输出不再是线性关系。通常使用Volterra级数［7］求解式（1）与式（2）组成的方程组，得到输入电压与输出位移的关系。根据Volterra级数理论，非线性系统的响应可以表示为各阶核函数与激励信号的卷积的形式，其框图如图2所示。

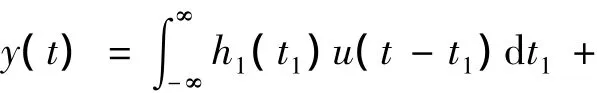
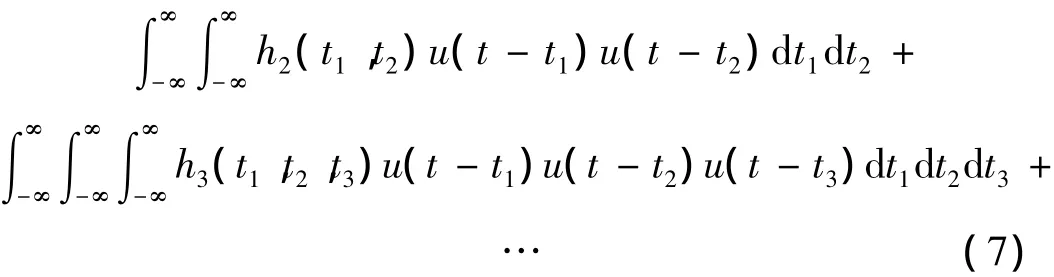
其中：u（t）为激励信号，y（t）为非线性系统的响应，h1表示系统的1阶核函数即线性冲激响应，h2与h3分别表示系统的2阶和3阶核函数，u（t）为输入。

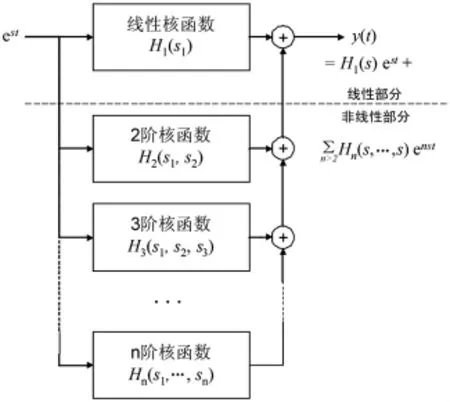
图2 非线性系统的Volterra模型框图Fig.2 Block diagram of nonlinear system modeling via Volterra series model

当输入信号x（t）=exp（s1t）时，系统线性响应在复频域的表达式为：

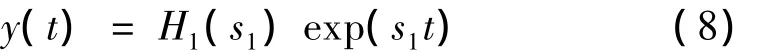
除线性响应外，输出中还具有输入信号的2次以上谐波响应。

输入信号x（t）=exp（s1t）+exp（s2t）时，只考虑到2阶响应输出，有：

式中前两项为线性响应。第3、4项对应着系统的2次谐波失真。H2（s1，s2）是对称的，有H2（s1，s2）=H2（s2，s1），故第5项系数为2，对应着系统的互调失真。

输入信号x（t）=exp（s1t）+exp（s2t）+exp（s3t）时，只考虑到3阶响应输出，有：

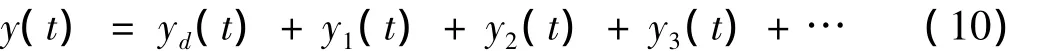
其中yd（t）为输出的直流分量，其形式在下文中给出。y1（t）是1阶核函数的响应，等同于线性响应。y2（t）与y3（t）分别是2、3阶核函数的响应，由谐波响应和互调响应构成。其具体形式如下：

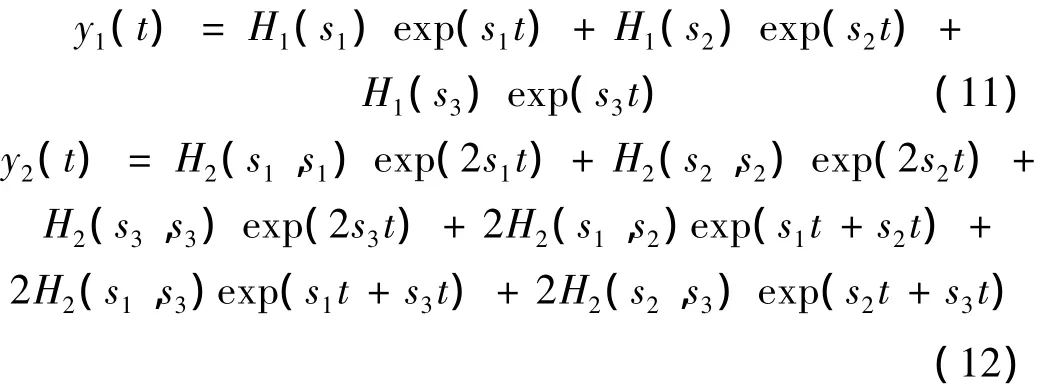
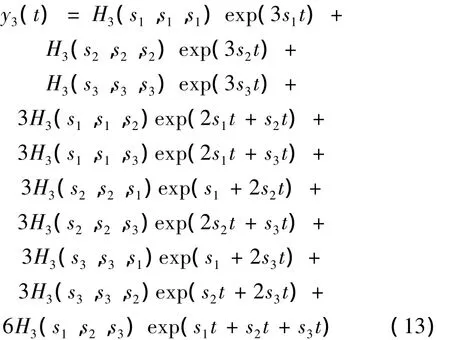
2次谐波响应参见y2（t）的前3项，2次互调响应为y2（t）的后3项。与之类似，3次谐波响应参见y3（t）的前3项，其余项为3次互调响应项。可见，随着分析阶数的增加，互调响应项的数量显著增加。

将Bl（x）、Kms（x）与Le（x）近似表示为二阶幂级数的形式，如下：

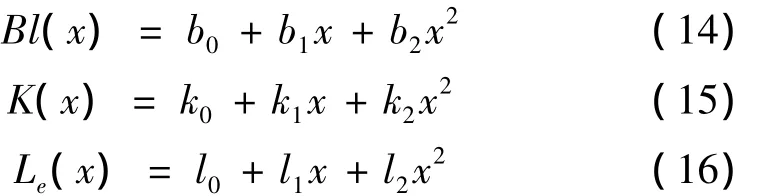
令输入U=exp（s1t）+exp（s2t）+exp（s3t），且位移为如式（10）的形式，代入式（3）和式（4），由谐波平衡法可求出线性核函数如式（6）及2、3阶核函数如下：

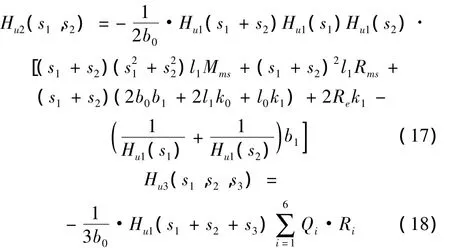
其中，系数Qi、Ri详见附录 1。

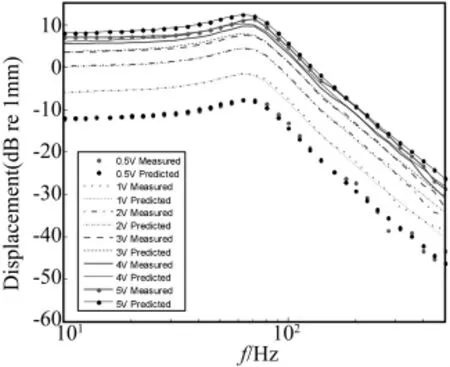
图3 不同输入电压下位移基频响应幅度Fig.3 Amplitude of linear response of diaphragm displacement in different input voltage

1.3 扬声器Volterra模型的局限性

在激励信号很小时，扬声器工作在弱非线性状态，可以通过上述Volterra核函数预测位移的基频响应及谐波、互调响应。若逐步增大激励信号，由Volterra核函数预测得到的结果便不再准确。图3比较了由Volterra核函数预测得到的位移基频响应结果和测量得到的位移响应结果。从图中可明显观察到，激励电压大于3 V以上，Volterra核函数的预测结果与实验结果的差异逐渐增大。造成Volterra模型误差增大的原因在于模型的近似处理，包括幂级数截断、Volterra级数的低近似等等。并且，扬声器参数发生的偏移，包括平衡位置偏移、单圈直流电阻升高、弹性部件的顺性改变等加剧了误差。Klippel的实验中也发现了上述现象，并将其称为非线性幅度压缩（Nonlinear Amplitude Compression）［8］。除幅度存在较大差异外，Volterra模型预测的共振频率并没有发生变化，而测量得到的位移共振频率随电压增大而升高。

2 改进的扬声器Volterra模型

2.1 大信号Volterra模型分析

在大信号输入扬声器的情况下会产生显著的谐波失真和互调失真。例如，向2阶Volterra系统输入单频激励信号，可表示为：

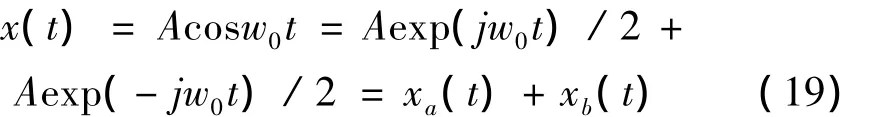
有响应：

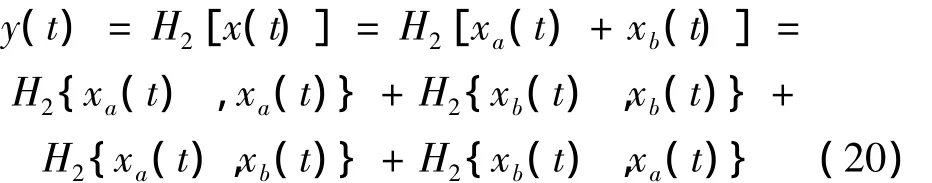
其中H2{·}为双线性Volterra算子。若2阶核函数时域形式为h2（τ1，τ2），有：

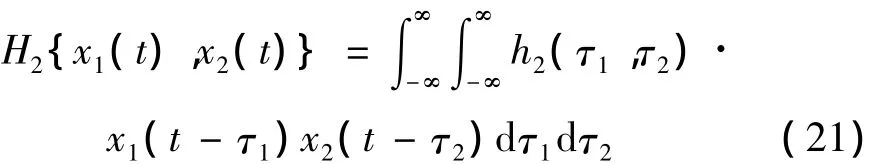
输出为：

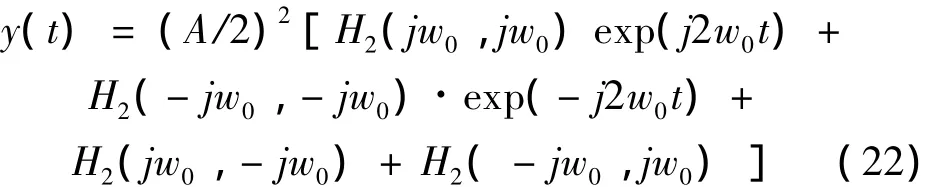
由共轭关系，前两项和后两项可以合并，化简为：

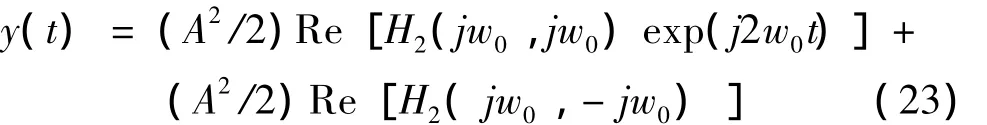
前一项为2阶谐波响应，后一项为2阶互调响应。互调响应频率为0，产生了直流分量。对于3阶Volterra系统的情况，可以求得单频信号激励下输出：

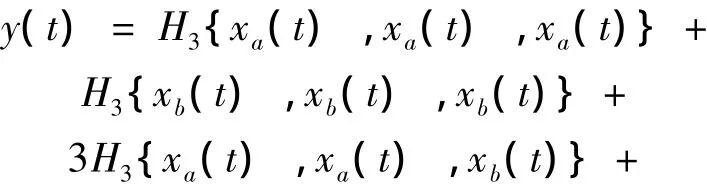
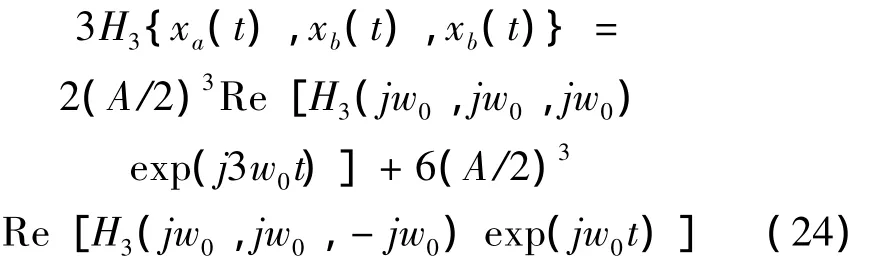
前一项为3阶谐波响应，后一项为互调响应。互调响应的频率与线性响应频率相同。

若只考虑1～3阶响应，对于单频输入的情况下，扬声器Volterra模型的输出如下

传统的扬声器Volterra模型仅包含式（25）中的1至3项，没有考虑高阶核函数的互调响应对线性响应的影响（第5项），也没有考虑直流分量对扬声器工作状态的影响（第4项）。然而，在激励信号幅度较大时，高阶互调项幅度显著增大，该影响变得不可忽略。

2阶及2阶以上的偶数阶核函数的部分互调响应产生直流分量，使扬声器振动的平衡位置偏移。在小振幅情况下，扬声器工作在Bl（x）、Kms（x）等参数斜率较小的平衡位置附近，参数随位移变化很小。大振幅情况下，平衡位置发生偏移，与位移相关的扬声器参数均受影响产生变化，同时振动的不对称引起失真增大。这解释了实验中位移共振频率发生变化的现象。另一方面，受到平衡位置偏移的影响，部分扬声器在大振幅下弹性部件可能发生异常，出现幅度压缩、不稳定、混沌和音圈跳出磁隙无法恢复的现象［8］。

3阶及3阶以上的奇数阶核函数的部分互调响应与扬声器线性响应频率一致，导致基频响应的变化，具体表现为幅度压缩和共振频率的变化。

2.2 改进方法

根据上述分析，可以得到一种改进的扬声器Volterra模型，其结构如图4所示。为说明本文所述方法，以下将对已知参数的扬声器进行3阶Volterra建模，计算得到已知输入下扬声器的各阶响应。

首先预测振膜的平衡位置偏移量xd。激励为式（19）的形式，则近似求得偏移量为：

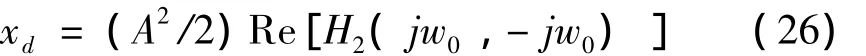
之后对如Bl（x）、Kms（x）和Le（x）等与位移相关的非线性参数进行更新。以Bl（x）为例，修正后结果为：

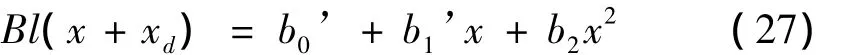
其中b0’=b0+b1xd+b2x2d，b1’=b1+2b2xd。

将更新后的参数代回。如此数次迭代后可得到预测偏移量和修正的非线性参数结果。

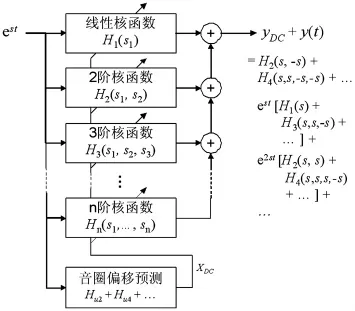
图4 改进的扬声器Volterra模型框图Fig.4 Block diagram of loudspeaker unit modeling via improved Volterra series model

最后将非线性参数代入各阶核函数，并考虑高阶核函数的互调项影响，可求出修正后的基频响应及各阶谐波响应。修正后的位移基频响应为：

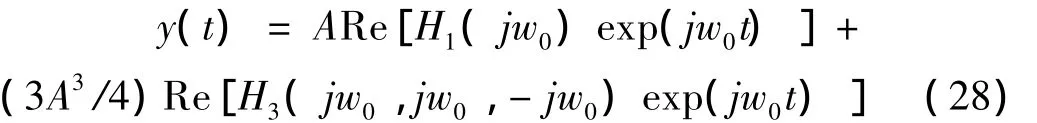
3 实验验证

3.1 实验设备

实验设备由激光传感器、测试支架、采集声卡、计算机和功率放大器组成，如图5所示。

扬声器振膜的振动测量有多种方式，可以通过位移、速度、加速度传感器和传声器进行测量。为了验证振膜平衡位置和位移基频响应的预测结果，实验中采用了ANR1282型激光位移传感器。该传感器的测量精度为4 μm，量程为40 mm，测量位移的频率范围为直流0～1 000 Hz。被测样品A与样品B为2种汽车用扬声器，参数见附录2。由于扬声器集中参数模型及Volterra模型均在低频使用，且扬声器样品的共振频率都在100 Hz以内，激光传感器的工作频率范围包含了上述频率，故可用于实验中。激光传感器和被测扬声器固定在支架上，通过调整扬声器的水平位置和激光传感器的垂直位置，可以把激光光束打在防尘帽的中心位置，使光束与振动表面垂直以获得最佳的信噪比。

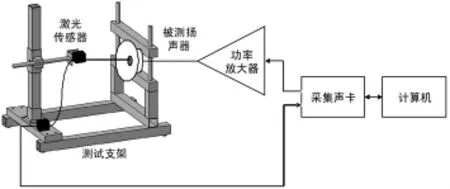
图5 实验装置Fig.5 Experiment setup

激励信号为离散对数扫频信号［9］，该信号由连接在计算机上的AudioFire 4专业声卡进行数模转换后，经功率放大器放大，输出到被测扬声器。激光传感器输出的信号为模拟信号，该信号接入声卡输入端，经模数转换后存储在计算机内。实验使用的专业声卡、功放等设备均经过6位半数字万用表Fluke 8845A校准。

扬声器在工作一段时间后，音圈温度将有所提高。此外，在扬声器工作结束时，振膜平衡位置并不稳定。为了排除上述因素影响，两次测量之间有10 min的冷却时间。

3.2 振膜平衡位置偏移量验证

由于被测扬声器参数已知，可使用改进的Volterra模型预测不同激励电压下振膜的平衡位置偏移情况，并通过实验测量振膜位移，以评价预测的结果。对样品A预测和实验得到的平衡位置偏移如图6。预测时只考虑到2阶核函数产生的平衡位置偏移量，因此存在一定的误差。

图7为样品A和样品B在激励信号频率等于位移共振频率情况下，以4 V脉冲正弦波激励得到的振膜平衡位置偏移量。0～10 s激励电压为0 V，振膜的偏移为0。10～20 s激励电压为4 V，出现较大的平衡位置偏移。由式（17）、式（26）可知，偏移的方向与扬声器参数b1、k1的符号有关。两个样品的参数b1和k1符号均相反，与测量得到的平衡位置偏移方向相反的现象一致。在20 s之后激励电压变为0，受到弹性部件的记忆效应影响，扬声器的音圈偏移没有立即回到原平衡位置。部分相关研究中也发现了这一现象［10-11］。从图中可以看出，样品A音圈偏移的恢复较样品B要缓慢得多，说明样品B与样品A相比性能更稳定。

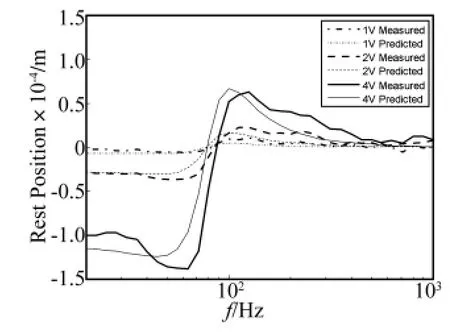
图6 预测和实验得到的振膜平衡位置Fig.6 Rest position of diaphragm by prediction or measurement

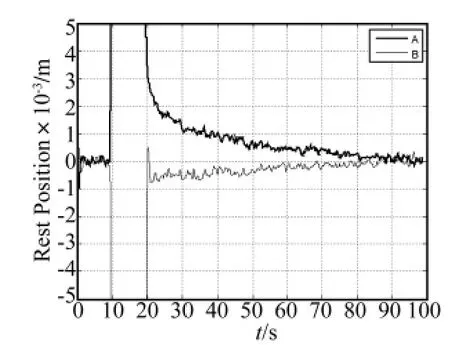
图7 扬声器工作后平衡位置偏移的恢复过程Fig.7 The recovery process of rest position varying after work

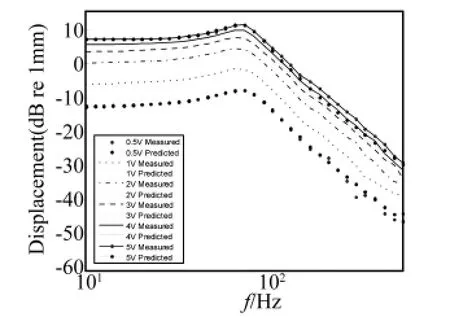
图8 不同输入电压下位移基频响应幅度Fig.8 Amplitude of linear response of diaphragm displacement in different input voltage

3.3 位移响应验证

图8为样品A使用改进的扬声器Volterra模型预测已知输入下振膜位移的基频响应结果。对比传统Volterra模型的预测结果（参见图3），由于考虑了高阶核函数互调造成的参数变化和幅度压缩，改进的Volterra模型的预测结果更接近于测量结果。此外，图9给出了1 V、2 V和4 V激励电压下样品B的实验结果和两种模型的预测结果。

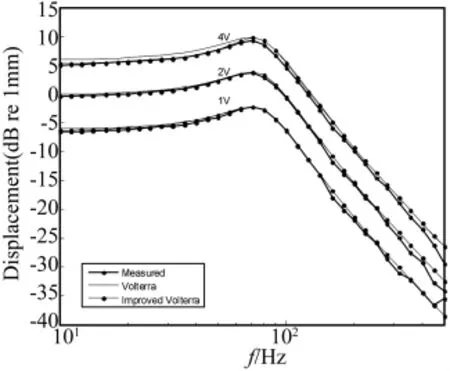
图9 不同输入电压下位移基频响应幅度Fig.9 Amplitude of linear response of diaphragm displacement in different input voltage

4 结论

为了改善传统的扬声器Volterra模型在激励信号幅度较大时预测得到的响应与测量结果误差较大的情况，本文提出了一种改进的扬声器Volterra模型。考虑到扬声器工作在大振幅状态时音圈偏移量对非线性参数造成的影响，结合扬声器的工作特点，音圈偏移量首先由偶数阶核函数计算得到。此外，在计算位移响应时引入了高阶核函数的互调项，使位移响应预测结果更为精确。

为了验证模型，扬声器的位移响应由一套激光位移测量系统测量得到。实验结果表明，音圈偏移量的预测结果与实验结果一致。并且，改进的扬声器Volterra模型可表征扬声器的幅度压缩现象。该模型可应用于扬声器的振动特性分析、参数辨识和固有非线性失真补偿。

［1］KaizerM. Modeling ofthe nonlinearresponse ofan electrodynamic loudspeaker by a volterra series expansion［J］.J.Audio Eng.Soc.，1987，35（6）：421-433.

［2］Klippel W.The mirror filter-A new basis for reducing nonlinear distortion and equalizing response in woofer systems［J］.J.Audio Eng.Soc.，1992，40（9）：675-691.

［3］Jeong H，Ih G.Harmonic balance method for estimating the nonlinear parameter of electrodynamic［J］.J.Audio Eng.Soc.，1996，44（4）：245-257.

［4］Bard D.Horn loudspeakers nonlinearity comparison and linearization using volterra series［R］.Audio Eng.Soc.Convention：124. Amsterdam：Audio Eng. Soc.，2008，7318.

［5］Walter F.An efficient approximation to the quadratic Volterra filter and its application in real-time loudspeaker linearization［J］.Signal Processing，1995，45（1）：97-113.

［6］ Klippel W.Loudspeaker nonlinearities-causes，parameters，symptoms［J］.J.Audio Eng.Soc.，2006，54（10）：907-939.

［7］Schetzen M.The volterra and wiener theories of nonlinear system［M］.New York：Wiley，1980.

［8］Klippel W.Optimal design of loudspeakers with nonlinear control［R］.Audio Eng.Soc.International Conference：32.New York：Audio Eng.Soc.，2007，18.

［9］杨 益，韦峻峰，温周斌，等.扬声器异常音的快速检测方法及其实验研究［J］.声学学报，2010，35（5）：562-570.

［10］ Klippel W. Prediction ofspeakerperformance athigh amplitudes［R］.Audio Eng.Soc.Convention：111.New York：Audio Eng.Soc.，2001，5418.

［11］ Pedersen B， Finn A. Time varying behaviorofthe loudspeaker suspension［R］.Audio Eng.Soc.Convention：127.New York：Audio Eng.Soc.，2009，7902.

附录1

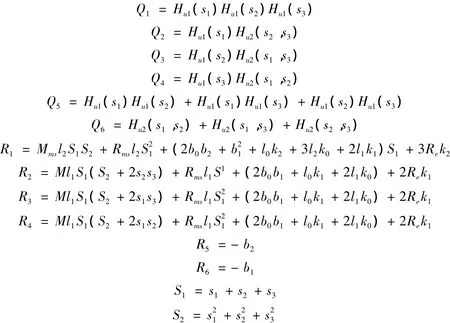
附录2

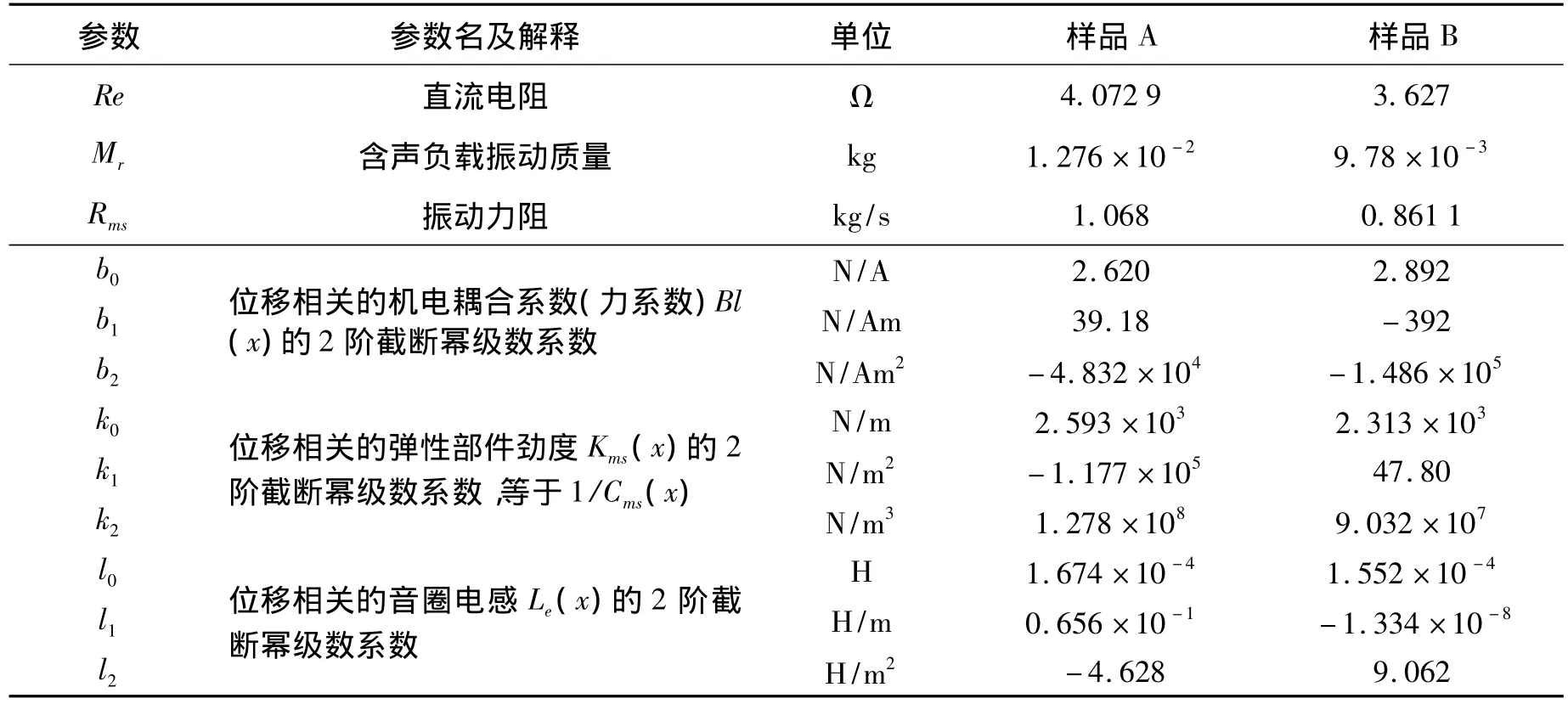
实验中使用的扬声器的非线性参数